PCA基本思想及其應用案例:企業綜合實力排序
主成分分析(PCA)基本原理
在數據建模中,我們會經常遇到多個變數的問題,而且在多數情況下,多個變數之間常常存在一定的相關性。當變數個數較多且變數之間存在複雜關係,會顯著增加分析問題的複雜性。如果有一種方法可以將多個變數綜合爲少數幾個代表性變數,使這些變數既能夠代表原始變數的絕大數資訊並且互不相幹,那麼無疑有助於對問題的分析和建模。這時,就可以考慮用主成分分析法。
PCA基本思想
PCA的本質其實就是對角化協方差矩陣。
PCA就是將高維的數據通過線性變換投影到低維空間上去,但這個投影可不是隨便投投,要遵循一個指導思想,那就是:找出最能夠代表原始數據的投影方法。
「最能代表原始數據」希望降維後的數據不能失真,也就是說,被PCA降掉的那些維度只能是那些噪聲或是冗餘的數據。
1:冗餘,就是去除線性相關的向量(緯度),因爲可以被其他向量代表,這部分資訊量是多餘的。
2:噪聲,就是去除較小特徵值對應的特徵向量,
因爲特徵值的大小就反映了變換後在特徵向量方向上變換的幅度,幅度越大,說明這個方向上的元素差異也越大,換句話說這個方向上的元素更分散。
3:實際上又回到了對角化,尋找極大線性無關組,然後保留較大的特徵值,去除較小特徵值,組成一個投影矩陣,
對原始樣本矩陣進行投影,得到降維後的新樣本矩陣。
協方差矩陣,能同時表現不同維度間的相關性以及各個維度上的方差。
協方差矩陣度量的是維度與維度之間的關係,而非樣本與樣本之間。
4:協方差矩陣的主對角線上的元素是各個維度上的方差(即能量),其他元素是兩兩維度間的協方差(即相關性)。我們要的東西協方差矩陣都有了,先來看「降噪」,讓保留下的不同維度間的相關性儘可能小,也就是說讓協方差矩陣中非對角線元素都基本爲零。達到這個目的的方式自然不用說,線代中講的很明確——矩陣對角化。而對角化後得到的矩陣,其對角線上是協方差矩陣的特徵值,它還有兩個身份:首先,它還是各個維度上的新方差;其次,它是各個維度本身應該擁有的能量(能量的概念伴隨特徵值而來)。這也就是我們爲何在前面稱「方差」爲「能量」的原因。通過對角化後,剩餘維度間的相關性已經減到最弱,已經不會再受「噪聲」的影響了,故此時擁有的能量應該比先前大了。看完了「降噪」,我們的「去冗餘」還沒完呢。對角化後的協方差矩陣,對角線上較小的新方差對應的就是那些該去掉的維度。所以我們只取那些含有較大能量(特徵值)的維度,其餘的就舍掉即可。
PCA基本步驟
1.對原始數據進行標準化處理
2.計算樣本相關係數矩陣
3.計算相關係數矩陣的特徵值
4.選擇重要的主成分,並寫出主成分表達式
5.計算主成分得分
**
看例題叭
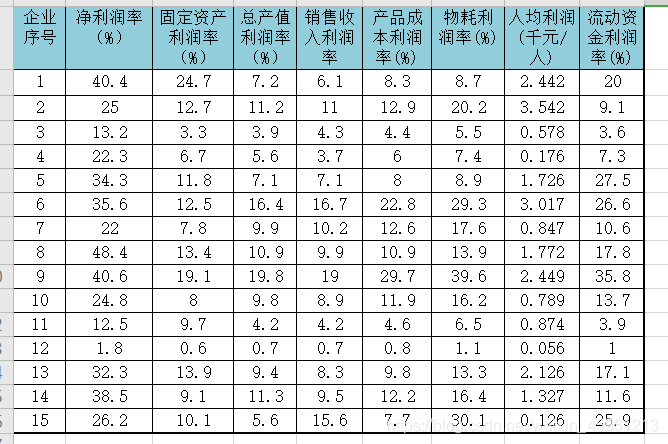
** 爲了系統分析IT類企業的經濟效益,選擇了8個不同的利潤指標,對15家企業進行了調研,並得到如表所示的數據,請根據這些數據進行綜合實力排序。
clc;
clear;
A=xlsread(‘C:\Users\Jonty\Desktop\Coporation_evaluation.xlsx’,‘B2:I16’);
%數據視覺化
a=size(A,1);
b=size(A,2);
for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));
end
%計算相關係數矩陣的特徵值和特徵向量
CM=corrcoef(SA);
[V,D]=eig(CM);
for j=1:b
DS(j,1)=D(b+1-j,b+1-j);
end
for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1));
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));
end
%選擇主成分及其對應的特徵向量
T=0.9
for k=1:b
if DS(k,3)>=T
Com_num=k;
break
end
end
%提取主成分對應的特徵向量
for j=1:Com_num
PV(:,j)=V(:,b+1-j);
end
%計算各評價物件的主成分得分
new_score = SA*PV
for i=1:a
total_score(i,1)=sum(new_score(i,:));
total_score(i,2)=i;
end
result_report=[new_score,total_score];
result_report=sortrows(result_report,-4);
輸出模型及報告結果
disp(‘特徵值及其貢獻率、累計貢獻率:’)
DS
disp(‘資訊保留率T對應的主成分數與特徵向量:’)
Com_num
PV
disp(‘主成分得分及其排序’)
result_report
執行程式得到如下結果
特徵值及其貢獻率、累計貢獻率:
DS =
5.7361 0.7170 0.7170
1.0972 0.1372 0.8542
0.5896 0.0737 0.9279
0.2858 0.0357 0.9636
0.1456 0.0182 0.9818
0.1369 0.0171 0.9989
0.0060 0.0007 0.9997
0.0027 0.0003 1.0000
資訊保留率T對應的主成分數與特徵向量:
Com_num =
3
PV =
0.3334 0.3788 0.3115
0.3063 0.5562 0.1871
0.3900 -0.1148 -0.3182
0.3780 -0.3508 0.0888
0.3853 -0.2254 -0.2715
0.3616 -0.4337 0.0696
0.3026 0.4147 -0.6189
0.3596 -0.0031 0.5452
主成分得分及其排序
result_report =
5.1936 -0.9793 0.0207 4.2350 9.0000
0.7662 2.6618 0.5437 3.9717 1.0000
1.0203 0.9392 0.4081 2.3677 8.0000
3.3891 -0.6612 -0.7569 1.9710 6.0000
0.0553 0.9176 0.8255 1.7984 5.0000
0.3735 0.8378 -0.1081 1.1033 13.0000
0.4709 -1.5064 1.7882 0.7527 15.0000
0.3471 -0.0592 -0.1197 0.1682 14.0000
0.9709 0.4364 -1.6996 -0.2923 2.0000
-0.3372 -0.6891 0.0188 -1.0075 10.0000
-0.3262 -0.9407 -0.2569 -1.5238 7.0000
-2.2020 -0.1181 0.2656 -2.0545 4.0000
-2.4132 0.2140 -0.3145 -2.5137 11.0000
-2.8818 -0.4350 -0.3267 -3.6435 3.0000
-4.4264 -0.6180 -0.2884 -5.3327 12.0000
由該分析結果可知,第9家企業的綜合實力最強
這個題中學到了corrcoef函數
這是求相關度的結果,對於一般的矩陣X,執行A=corrcoef(X)後,A中每個值的所在行a和列b,反應的是原矩陣X中相應的第a個列向量和第b個列向量的相似程度(即相關係數)。計算公式是:C(1,2)/SQRT(C(1,1)*C(2,2)),其中C表示矩陣[f,g]的協方差矩陣,假設f和g都是列向量(這兩個序列的長度必須一樣才能 纔能參與運算),則得到的(我們感興趣的部分)是一個數。以預設的A=corrcoef(f,g)爲例,輸出A是一個二維矩陣(對角元恆爲1),我們感興趣的f和g的相關係數就存放在A(1,2)=A(2,1)上,其值在[-1,1]之間,1表示最大的正相關,-1表示絕對值最大的負相關
eig函數
在MATLAB中,計算矩陣A的特徵值和特徵向量的函數是eig(A),常用的呼叫格式有5種:
E=eig(A):求矩陣A的全部特徵值,構成向量E。
[V,D]=eig(A):求矩陣A的全部特徵值,構成對角陣D,並求A的特徵向量構成V的列向量。
[V,D]=eig(A,‘nobalance’):與第2種格式類似,但第2種格式中先對A作相似變換後求矩陣A的特徵值和特徵向量,而格式3直接求矩陣A的特徵值和特徵向量。
E=eig(A,B):由eig(A,B)返回N×N階方陣A和B的N個廣義特徵值,構成向量E。
[V,D]=eig(A,B):由eig(A,B)返回方陣A和B的N個廣義特徵值,構成N×N階對角陣D,其對角線上的N個元素即爲相應的廣義特徵值,同時將返回相應的特徵向量構成N×N階滿秩矩陣,且滿足AV=BVD。