二元樹的基礎---四種遍歷方式的

 

1. 基本介紹

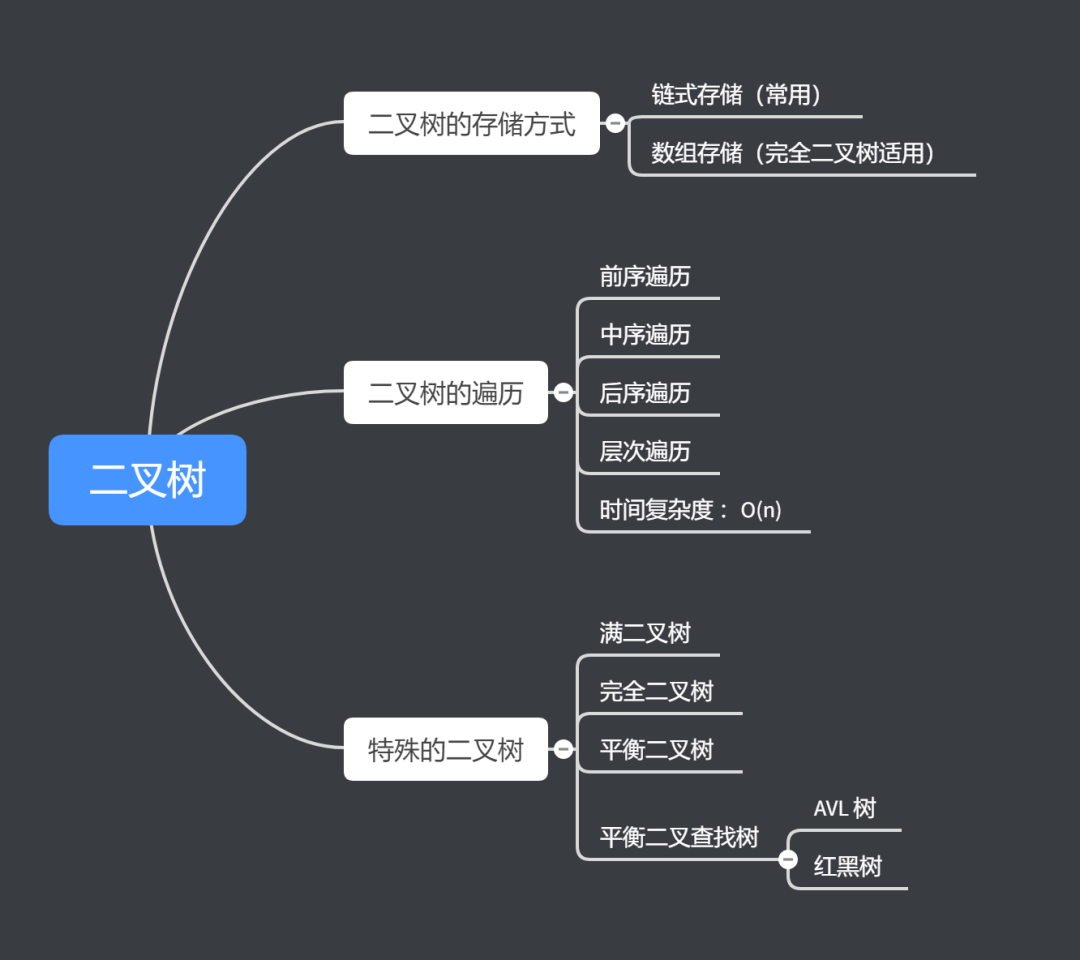
樹結構多種多樣，但是最常用的還是二元樹。二元樹中每個節點最多有兩個子節點，這兩個節點分別是左子節點和右子節點。注意：不要求都有兩個子節點，可以只有左子節點，也可以只有右子節點。

 

2. 二元樹的儲存

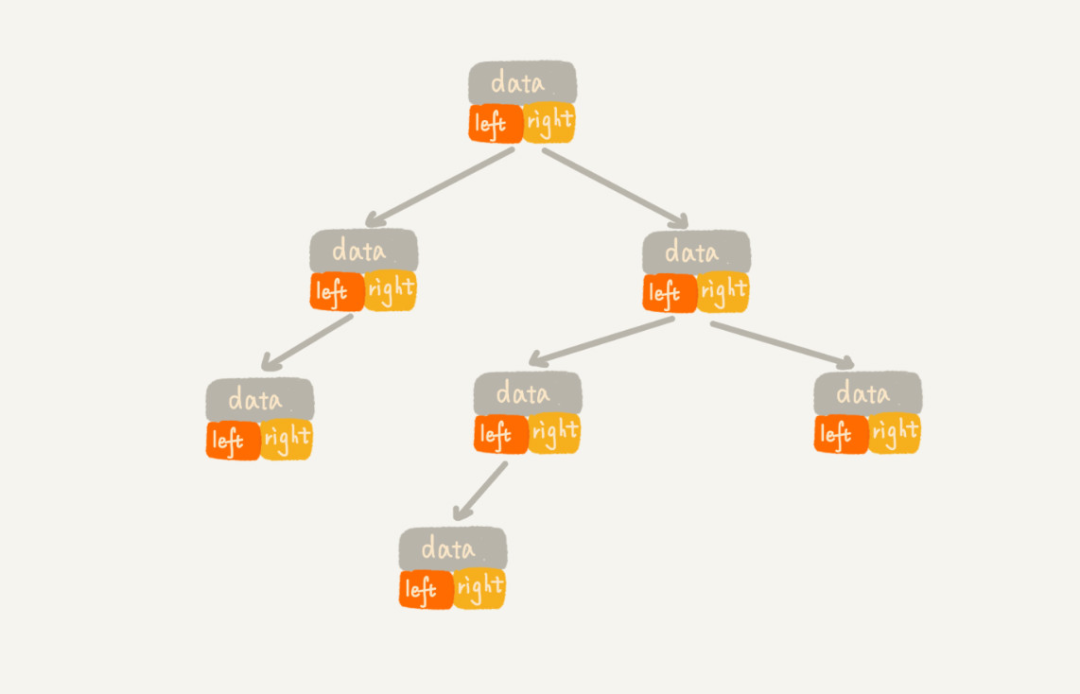
2.1. 鏈式儲存法

每個節點至少有三個欄位，其中一個儲存數據，另外兩個是指向左右子節點的指針。這種儲存方式比較常用，大部分二元樹程式碼都是通過這種結構來實現的。

 

2.2. 陣列儲存法

我們把根節點儲存在下標 i=1 的位置，它的左子節點儲存在下標爲 2 * i 的位置，右子節點儲存在下標爲 2*i+1 的位置。以此類推，B 節點、C 節點的左右子節點都按照這種規律進行儲存，最終如下圖所示。

綜上，如果節點 X 儲存在陣列中下標爲 i 的位置，那麼下標爲 2*i 的位置儲存的就是它的左子節點，下標爲 2*i+1 的位置儲存的就是它的右子節點。反過來，i/2 的位置儲存的就是它的父節點。一般情況下，爲了方便計算，根節點會被儲存在下標爲 1 的位置。

 

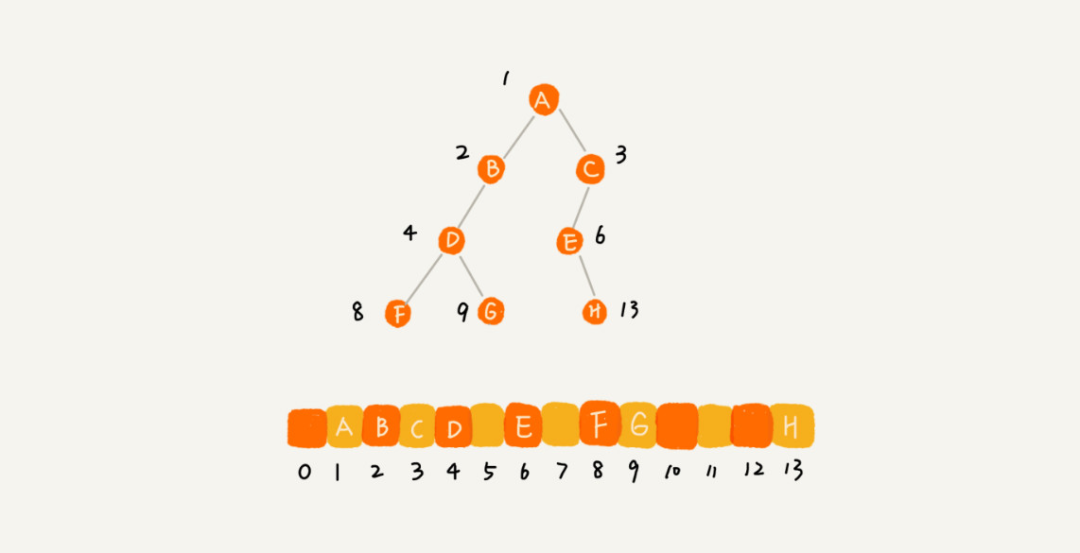
通過上述可以看到，針對一般樹來說，使用陣列的方式儲存樹會浪費比較多的儲存空間。但是針對下文會提到的滿二元樹或者完全二元樹來說，陣列儲存的方式是最節省記憶體的一種方式。因爲陣列儲存時，不需要再儲存額外的左右子節點的指針。

3. 二元樹的遍歷

二元樹的遍歷就是將二元樹中的所有節點遍歷列印出來。經典的方法有三種，前序遍歷、中序遍歷和後序遍歷，還可以按層遍歷（個人理解的按層遍歷其實就是按照圖的廣度優先遍歷方法來進行遍歷）。

前、中、後是根據節點被列印的先後 先後來進行區分的：前序就是先列印節點本身，之後再列印它的左子樹，最後列印它的右子樹；中序就是先列印節點的左子樹，再列印節點本身，最後列印右子樹，即把節點放中間的位置輸出；後序就是先列印節點的左子樹，再列印節點的右子樹，最後列印節點本身。如下圖所示

 

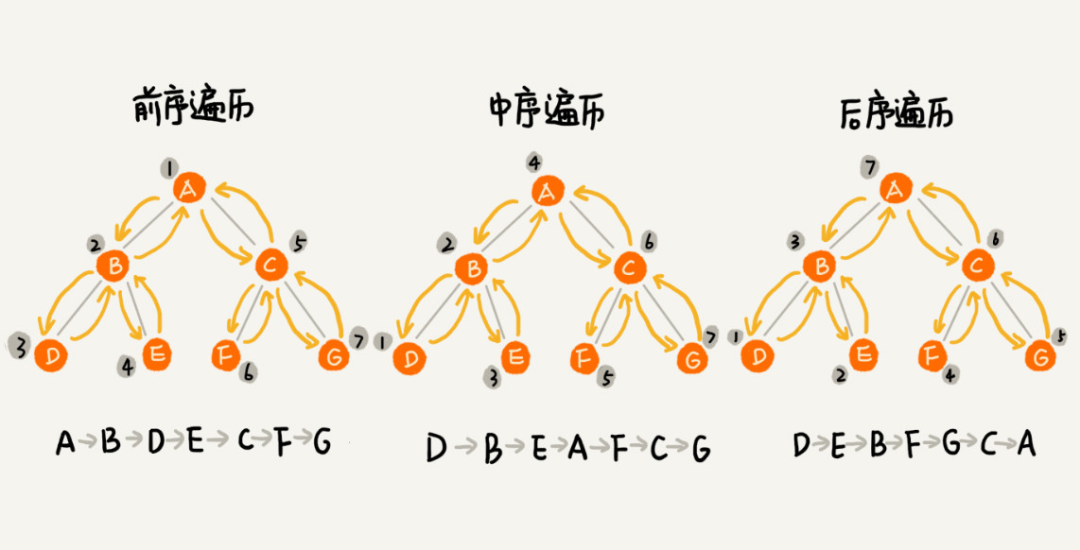
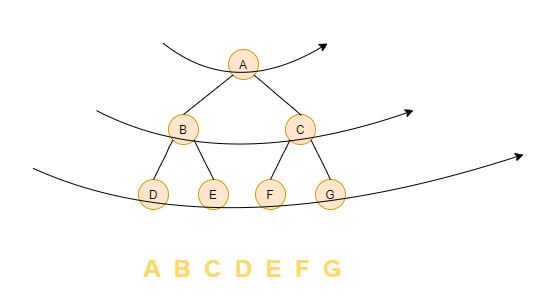
按層遍歷類似於圖的廣度優先遍歷，先列印第一層的節點，之後再依次列印第二層的節點，以此類推。

 

3.1. 程式碼實現

實際上，二元樹的前、中、後序遍歷是一個遞回的過程。比如，前序遍歷，其實就是先列印根節點，然後遞回遍歷左子樹，最後遞回遍歷右子樹。遞回遍歷左右子樹其實就跟遍歷根節點的方法一樣。下面 下麪先寫出這三者遍歷的遞推公式：

前序遍歷的遞推公式：
preOrder(r) = print r ---> preOrder(r->left) ---> preOrder(r->right)

中序遍歷的遞推公式：
inOrder(r) = inOrder(r--->left) ---> print r ---> inOrder(r->right)

後序遍歷的遞推公式：
postOrder(r) = postOrder(r->left) ---> postOrder(r->right) --->print r

之後將遞推公式轉化爲程式碼如下所示：

/**
 * 前序遍歷
 */
public void preOrder(Node tree) {
    if (tree == null) {
        return;
    }

    System.out.print(tree.data + "  ");

    preOrder(tree.left);

    preOrder(tree.right);
}

/**
 * 中序遍歷
 */
public void inOrder(Node tree) {
    if (tree == null) {
        return;
    }

    inOrder(tree.left);

    System.out.print(tree.data + "  ");

    inOrder(tree.right);
}

/**
 * 後序遍歷
 */
public void postOrder(Node tree) {
    if (tree == null) {
        return;
    }

    postOrder(tree.left);

    postOrder(tree.right);

    System.out.print(tree.data + "  ");
}

遞回程式碼的關鍵，在於寫出遞推公式。而遞推公式的關鍵在於，A 問題可以被拆解成 B、C 兩個問題。假設要解決 A 問題，那麼假設 B、C 問題已經解決了。那麼在 B、C 已經解決的提前下，看如何利用 B、C 來解決 A 。千萬不要模擬計算機一層一層想下去，否則你就會發現你自己都不知道在哪了。

下面 下麪是按層遍歷的程式碼，按層遍歷需要用到佇列的入隊和出隊等操作。先將根節點放入到佇列中，然後回圈從佇列中取節點（出隊），再將該節點的左右子節點入隊。出隊的順序就是層次遍歷的結果。

/**
 * 層次遍歷
 */
public void BFSOrder(Node tree) {
    if (tree == null) {
        return;
    }

    Queue<Node> queue = new LinkedList<>();
    Node temp = null;
    queue.offer(tree);
    while (!queue.isEmpty()) {
        temp = queue.poll();
        System.out.print(temp.data + "  ");
        if (temp.left != null) {
            queue.offer(temp.left);
        }

        if (temp.right != null) {
            queue.offer(temp.right);
        }
    }
}

完整的程式碼可檢視 github 倉庫 https://github.com/DawnGuoDev/algos ，這個倉庫將主要包含常用數據結構及其基本操作的手寫實現（Java），也會包含常用演算法思想經典例題的實現（Java）。在程式鍋找到工作之前，這個倉庫將會保持更新狀態，在此之間學到的關於數據結構和演算法的知識或者實現也都會往裏面 commit，所以趕緊來 star 哦。

3.2. 時間複雜度

遍歷過程中的次數就是存取所有節點的所需的次數，而每個節點最多被存取兩次，因此遍歷的時間複雜度是跟節點的個數 n 成正比的，即遍歷的時間複雜度是 O(n)。

4. 特殊的二元樹

4.1. 滿二元樹

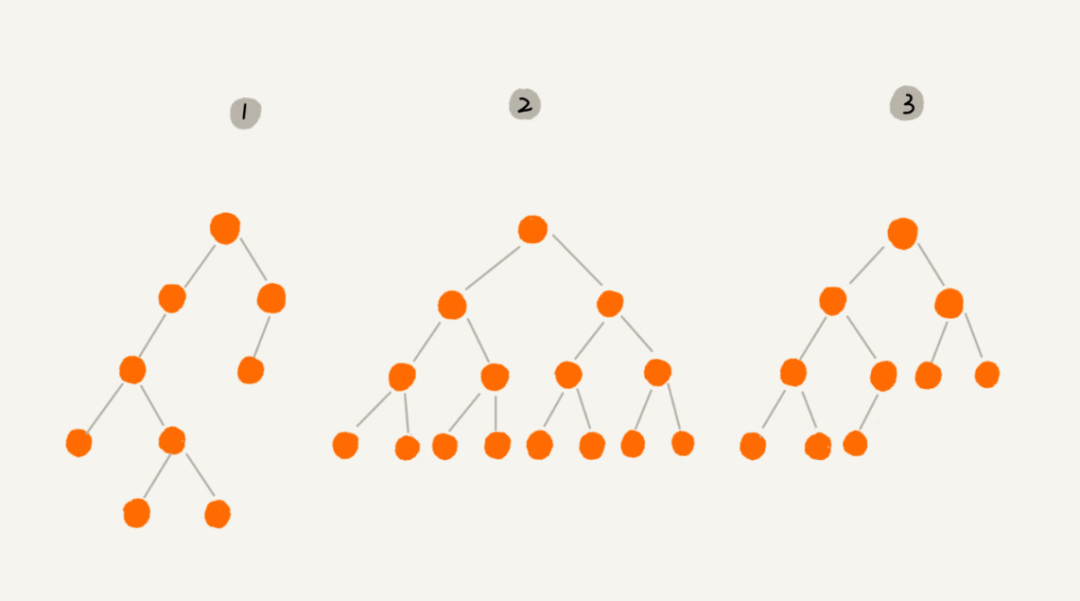
滿二元樹是一種特殊的二元樹，而且還是完全二元樹的一種特殊情況。如上圖編號 2 的那棵樹所示，葉子節點全在底層，除了葉子節點之外，每個節點都有左右兩個子節點。

4.2. 完全二元樹

完全二元樹也是一種特殊的二元樹。如上圖編號 3 的那棵樹所示，葉子節點都在最底下兩層，最後一層的葉子節點都靠左排列，並且除了最後一層，其他層的節點個數都達到最大。

 

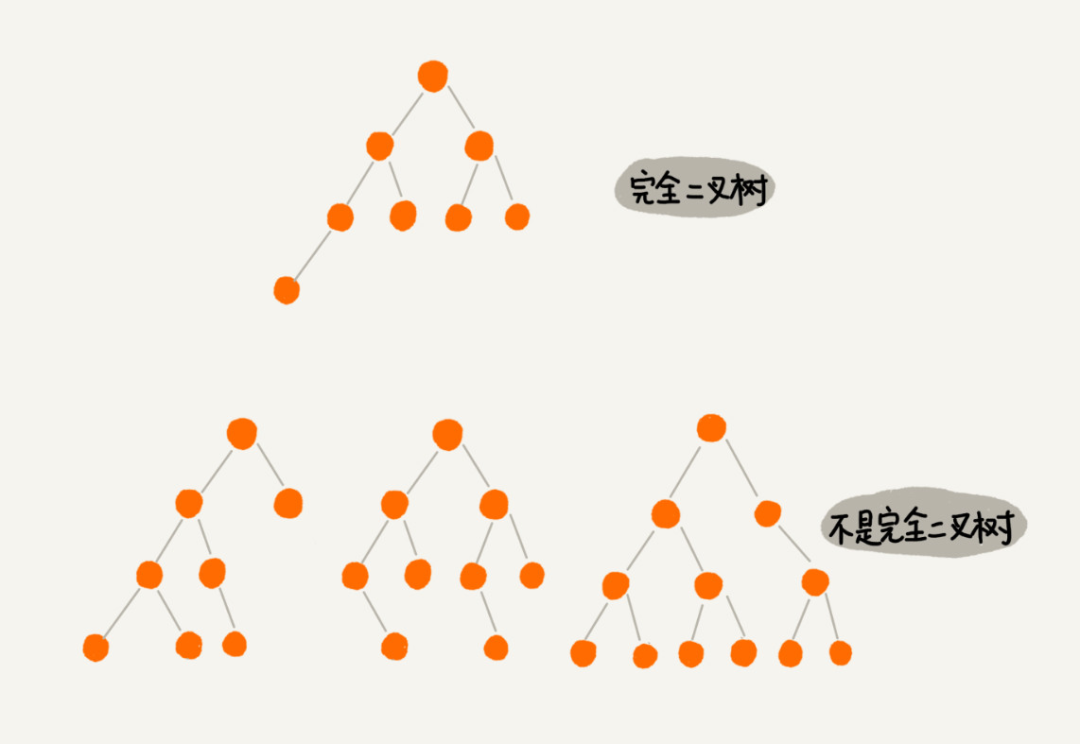
完全二元樹的特徵使得它可以使用陣列就可以很好地儲存數據。完全二元樹要求最後一層的葉子節點靠左排列也是因爲如此。

4.2.1. 完全二元樹的儲存

• 鏈式儲存

  就是上面提到的那種方式。

• 陣列儲存

  完全二元樹使用陣列儲存時，如下圖所示。我們發現使用陣列來儲存完全二元樹是一種很節省記憶體的方式。這也是完全二元樹被作爲一種特殊樹的原因，也是完全二元樹要求最後一層的子節點必須都靠左的原因。

  在講解堆或者堆排序的時候，堆其實也是一種完全二元樹，最常用的儲存方式就是陣列。

  

   

4.3. 其他特殊的二元樹

其他特殊的二元樹還有二叉查詢樹、平衡二叉查詢樹等。因爲這兩種特殊的樹涵蓋的知識比較多，所以會將其分開進行單獨講解。

5. 附 Github

整個系列的程式碼可檢視 github 倉庫 https://github.com/DawnGuoDev/algos ，這個倉庫將主要包含常用數據結構及其基本操作的手寫實現（Java），也會包含常用演算法思想經典例題的實現（Java）。在接下來一年內，這個倉庫將會保持更新狀態，在此之間學到的關於數據結構和演算法的知識或者實現也都會往裏面 commit，所以趕緊來 star 哦。