【推薦系統】聚類演算法-K-Means演算法
2020-08-12 20:38:47
K-means演算法思想
K-means演算法是最爲經典的基於劃分的聚類方法。是一種比較簡單的演算法。其基本思想和核心內容就是在演算法開始時隨機給定若幹(K)箇中心,按照最近距離原則將樣本點分配到各個中心點,之後按平均法計算聚類集的中心點位置,從而重新確定新的中心點位置。這樣不斷地迭代下去直至聚類集內的樣本滿足閾值爲止。
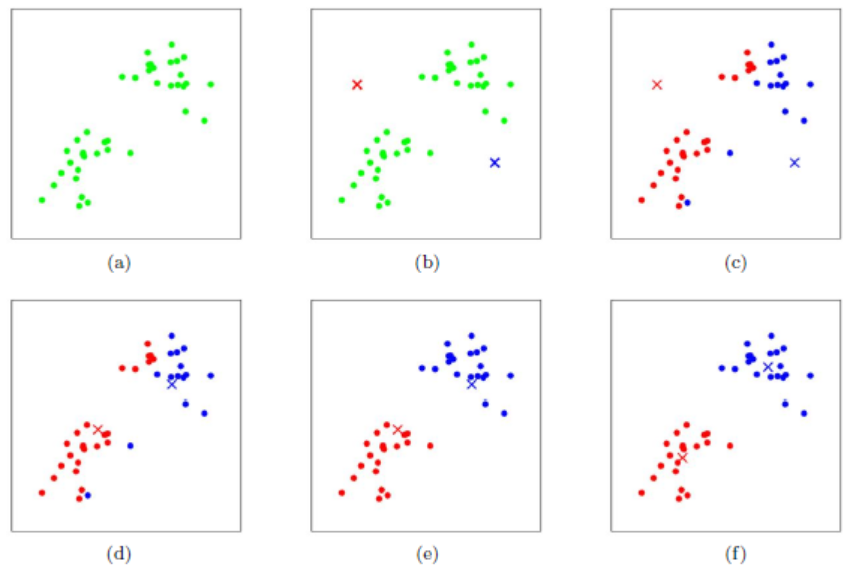
單單概念無法理解k-means演算法,接着看圖a,如果普通人,很容易就可以區分出來兩類數據。但是機器卻無法區分,畢竟機器是死腦筋。如果機器來區分的話有以下步驟
- 機器則隨機定義了兩個點紅點和藍點,如圖b。
- 所有的點計算到紅點和藍點的距離,距離哪個近即屬於哪一個集合,計算完成之後分類結束得到圖c。
- 顯然圖c不是最好的結果,每個集合計算該集合的質心(中心點)。然後重複步驟2。質心的位置變化越來越小,直到原來的質心到計算出來的質心的距離小於提前設定好的閾值的時候,即可認爲分類結束,如圖d,e,f。
K-means演算法Scala實現
kmeans.txt ,這是libsvm數據格式。
0 1:0.0 2:0.0 3:0.0
1 1:0.1 2:0.1 3:0.1
2 1:0.2 2:0.2 3:0.2
3 1:9.0 2:9.0 3:9.0
4 1:9.1 2:9.1 3:9.1
5 1:9.2 2:9.2 3:9.2
def main(args: Array[String]): Unit = {
val spark = SparkSession.builder().appName("kmeans")
.master("local[2]")
.getOrCreate();
//libsvm是一種數據格式
val dataset = spark.read.format("libsvm").load("C:\\Users\\archermind\\Desktop\\ml-1m\\kmeans.txt")
// Trains a k-means model.
// k 表示分爲兩類
val kmeans = new KMeans().setK(2).setSeed(1l)
val model = kmeans.fit(dataset)
// Make predictions
val predictions = model.transform(dataset)
predictions.show(false)
/* predictions的內容如下
+-----+-------------------------+
|label|features |
+-----+-------------------------+
|0.0 |(3,[],[]) |
|1.0 |(3,[0,1,2],[0.1,0.1,0.1])|
|2.0 |(3,[0,1,2],[0.2,0.2,0.2])|
|3.0 |(3,[0,1,2],[9.0,9.0,9.0])|
|4.0 |(3,[0,1,2],[9.1,9.1,9.1])|
|5.0 |(3,[0,1,2],[9.2,9.2,9.2])|
|6.0 |(3,[0,1,2],[3.1,3.2,3.3])|
+-----+-------------------------+
*/
//用於驗證羣集內一致性的一種度量。取值範圍是1到-1,其中接近1的值表示一個羣集中的點靠近同一羣集中的其他點
val evaluator = new ClusteringEvaluator()
val silhouette = evaluator.evaluate(predictions)
println(s"Silhouette with squared euclidean distance = $silhouette")
// 輸入分類結果
println("Cluster Centers: ")
model.clusterCenters.foreach(println)
/** 輸出結果
* Silhouette with squared euclidean distance = 0.9997530305375207
* 分類結果
* Cluster Centers:
* [0.1,0.1,0.1]
* [9.1,9.1,9.1]
*/
}
如上所示,可以認爲在三維座標系中有6個點,分成了兩類數據。
新增第6個數據,分成3類,有如下輸出
0 1:0.0 2:0.0 3:0.0
1 1:0.1 2:0.1 3:0.1
2 1:0.2 2:0.2 3:0.2
3 1:9.0 2:9.0 3:9.0
4 1:9.1 2:9.1 3:9.1
5 1:9.2 2:9.2 3:9.2
6 1:3.1 2:3.2 3:3.3輸入結果如下:
Silhouette with squared euclidean distance = 0.9997530305375207
Cluster Centers:
[0.1,0.1,0.1]
[9.1,9.1,9.1]
注:libsvm是一種數據格式,格式如下
<label> <index1>:<value1> <index2>:<value2> ...
其中
參考地址: