稀疏陣列與佇列

1、前言

1.1 數據結構和演算法的重要性

演算法是程式的靈魂，優秀的程式可以在海量數據計算時，依然保持高速計算。

一般來講 程式會使用了記憶體計算框架(比如Spark)和快取技術(比如Redis等)來優化程式,再深入的思考一下，這些計算框架和快取技術， 它的核心功能是哪個部分呢？

拿實際工作經歷來說, 在Unix下開發伺服器程式，功能是要支援上千萬人同時線上， 在上線前，做內測，一切OK,可上線後，伺服器就支撐不住了, 公司的CTO對程式碼進行優化，再次上線，堅如磐石。你就能感受到程式是有靈魂的，就是演算法。

目前程式設計師面試的門檻越來越高，很多一線IT公司(大廠)，都會有數據結構和演算法面試題(負責的告訴你，肯定有的)。

如果你不想永遠都是程式碼工人,那就花時間來研究下數據結構和演算法。

1.2 數據結構和演算法的關係

數據data結構(structure)是一門研究組織數據方式的學科，有了程式語言也就有了數據結構.學好數據結構可以編寫出更加漂亮,更加有效率的程式碼。
要學習好數據結構就要多多考慮如何將生活中遇到的問題,用程式去實現解決。
程式 = 數據結構 + 演算法
數據結構是演算法的基礎, 換言之，想要學好演算法，需要把數據結構學到位

1.3 數據結構的基本結構

線性結構和非線性結構
數據結構包括：線性結構和非線性結構。

線性結構

• 線性結構作爲最常用的數據結構，其特點是數據元素之間存在一對一的線性關係。
• 線性結構有兩種不同的儲存結構，即順序儲存結構和鏈式儲存結構。
  - 順序儲存的線性表稱爲順序表，順序表中的儲存元素是連續的。
  - 鏈式儲存的線性表稱爲鏈表，鏈表中的儲存元素不一定是連續的，元素節點中存放數據元素以及相鄰元素的地址資訊。
• 線性結構常見的有：陣列、佇列、鏈表和棧，後面會詳細敘述。

非線性結構

非線性結構包括：二維陣列，多維陣列，廣義表，樹結構，圖結構。

2、稀疏陣列

2.1 稀疏陣列的應用場景

先看一個實際的需求

​ 1. 編寫的五子棋程式中，有存檔退出和續上盤的功能。

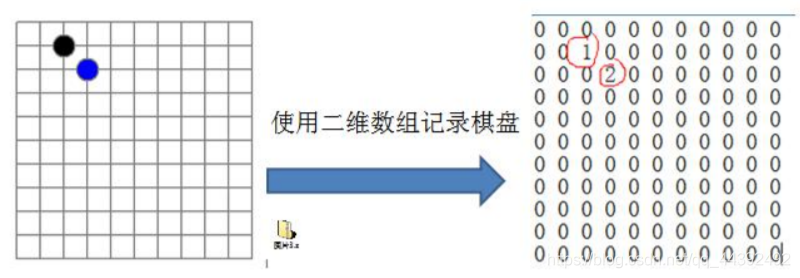
分析問題:
因爲該二維陣列的很多值是預設值0, 因此記錄了很多沒有意義的數據.->稀疏陣列。

2.2 稀疏陣列的介紹和說明

2.2.1 稀疏陣列基本介紹

當一個數組中大部分元素爲０，或者爲同一個值的陣列時，可以使用稀疏陣列來儲存該陣列。
稀疏陣列的處理方法是：

• 記錄陣列一共有幾行幾列，有多少個不同的值；
• 把具有不同值的元素的行列及值記錄在一個小規模的陣列中，從而縮小程式的規模。

2.2.2 稀疏陣列舉例說明

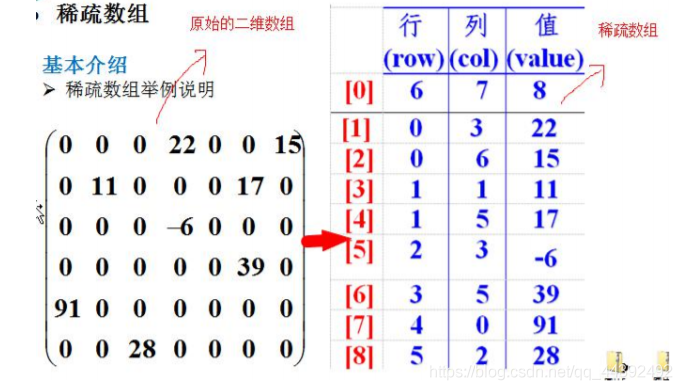
2.3 二維陣列轉稀疏陣列過程

1. 將原始稀疏陣列用二維陣列儲存，需要n行m列的陣列,記錄n*m個數據;
2. 如果使用稀疏陣列儲存,在稀疏陣列的
   2.1 第一行第一列記錄原始陣列總行數,
   2.2 第一行第二列記錄原始陣列的總列數
   2.3 第一行第三列記錄原始陣列非零值的個數,
3. 在稀疏陣列的第二行開始的每一行分別記錄每一個非零值的行值、列值、具體數據大小,
4. 使用稀疏陣列即可將原始陣列由n行n列n*m個值的二維陣列, 轉換爲一個空間較小的二維陣列。

2.4 稀疏陣列轉換的思路分析及實現

應用範例

使用稀疏陣列，來保留類似前面的二維陣列(棋盤、地圖等等)
把稀疏陣列存檔，並且可以從新恢復原來的二維陣列數
整體思路分析

1、二維陣列 轉 稀疏陣列的思路

1. 遍歷 原始的二維陣列，得到有效數據的個數 sum
2. 根據sum 就可以建立 稀疏陣列 sparseArr int[sum+1] [3]
3. 將二維陣列的有效數據數據存入到 稀疏陣列 (稀疏陣列每行分別記錄原始陣列 行、列、值)

2、稀疏陣列轉原始的二維陣列的思路

1. 先讀取稀疏陣列的第一行，根據第一行的數據,建立原始的二維陣列，如圖的 chessArr2 = int [11][11]
2. 在讀取稀疏陣列後幾行的數據，並賦給原始的二維陣列,即可.

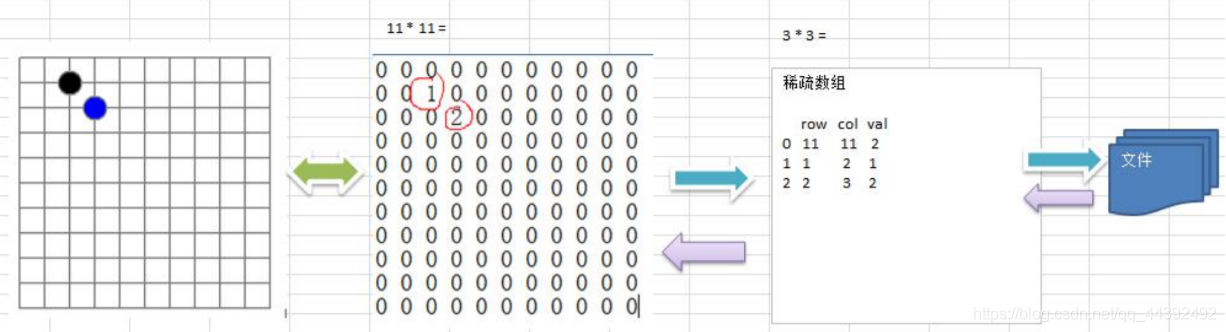
public class sparseArray {
    public static void main(String[] args) {
        /*棋盤稀疏陣列壓縮儲存
        1.建立8*8棋盤*/
        int chessArray[][]=new int[8][8];
        chessArray[2][2]=1;//黑棋
        chessArray[3][3]=1;
        chessArray[4][4]=1;
        chessArray[2][3]=2;//白棋
        chessArray[2][4]=2;
        chessArray[3][4]=2;

        int sum=0;
        //列印且遍歷二維陣列
        System.out.println("原始陣列"+chessArray.length+"*"+chessArray[0].length);
        for (int[] row:chessArray){
            for (int data: row){
                if (data != 0) { sum++; }
                System.out.print(data+"\t");
            }
            System.out.println();
        }
        System.out.println("棋子的數量："+sum);//有棋子的數量

        //建立稀疏陣列且爲其第一行賦初值
        int sparseArray1[][]=new int[sum+1][3];
        sparseArray1[0][0]=8;//行
        sparseArray1[0][1]=8;//列
        sparseArray1[0][2]=sum;//個數

        //遍歷二維陣列，將非0數值存放到sparArray1中
        //原始陣列 轉 稀疏陣列
        int count=0;
        for (int i=0;i<8;i++){
            for (int j=0;j<8;j++){
                if (chessArray[i][j]!=0){
                    count++; //count記錄行數
                    sparseArray1[count][0]=i;
                    sparseArray1[count][1]=j;
                    sparseArray1[count][2]=chessArray[i][j];
                }
            }
        }

        System.out.println("稀疏陣列");
        for (int[] row:sparseArray1){
            for (int data: row){
                System.out.print(data+"\t");
            }
            System.out.println();
        }

        //稀疏陣列 轉棋盤陣列
        int r=sparseArray1[0][0];
        int c= sparseArray1[0][1];
        int chessArray2[][]=new int[r][c];//根據第一行的值建立原始陣列大小

        for (int i=1;i<sum+1;i++){ //分別讀取稀疏陣列數據 賦值給 原始陣列
                int row,col;
                row=sparseArray1[i][0];
                col=sparseArray1[i][1];
               chessArray2[row][col]=sparseArray1[i][2];
        }
        /*for (int i=1;i<sparseArray1.length;i++){
            chessArray2[sparseArray1[i][0]][sparseArray1[i][1]]=sparseArray1[i][2];
        }*/
        System.out.println("原始陣列");
        sparseArray.print(chessArray2);

    }

    //列印棋盤
    public static void print(int Array[][]){
        for (int i=0;i<Array.length;i++){
            for (int j=0;j<Array[0].length;j++){
                System.out.print(Array[i][j]+"\t");
            }
            System.out.println();
        }
    }
}

3、佇列

3.1 佇列的應用場景和介紹

佇列的一個使用場景
排隊打飯、高速收費站出入口，單向隧道行駛

• 銀行排隊的案例:
  

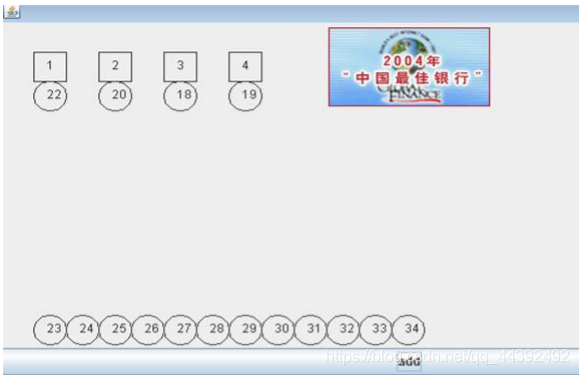
3.1.1佇列介紹

• 佇列是一個有序列表，可以用陣列或是鏈表來實現。

• 遵循先入先出的原則。即：先存入佇列的數據，要先取出。後存入的要後取出 （先入先出，後入後出）

示意圖：(使用陣列模擬佇列示意圖)

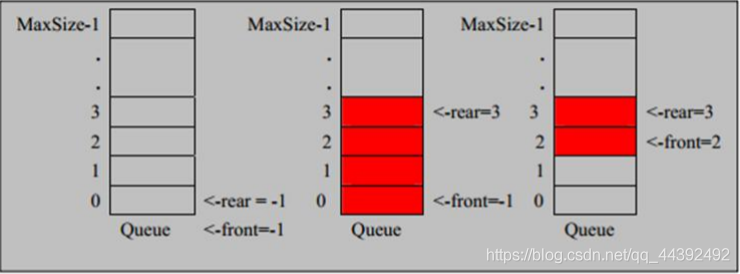
佇列初始的情況

1. Queue–>代表類Queue
2. rear -->代表隊尾，初始化爲-1
3. front–>代表隊首，初始化爲-1
4. MaxSize-1–>佇列的最大容量(從0開始計數，需減一)

圖二：向佇列增加數據的情況

• 當數據增加時rear變大，front不變

圖三：從佇列取數據的情況

• 當數據取出時front變大，rear不變

3.2 陣列模擬佇列的思路分析及實現

3.2.1 陣列模擬佇列

• 佇列本身是有序列表，若使用陣列的結構來儲存佇列的數據，則佇列陣列的宣告如下圖, 其中 maxSize 是該佇列的最大容量。

• 因爲佇列的輸出、輸入是分別從前後端來處理，因此需要兩個變數 front及rear分別記錄佇列前後端的下標，front會隨着數據輸出而改變，而 rear則是隨着數據輸入而改變，
  如圖所示:

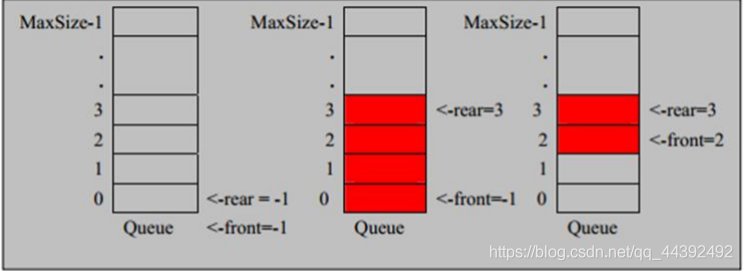
3.2.1 陣列新增佇列思路分析

當我們將數據入佇列、出佇列時 的處理需要有兩個步驟：

入佇列

• 將尾指針往後移：rear+1 , 當front == rear 【空】
• 若尾指針 rear 小於佇列的最大下標 maxSize-1，則將數據存入 rear所指的陣列元素中，否則無法存入數據。 rear = = maxSize - 1[佇列滿]
  出佇列
• 將頭指針往後移：front+1 , 當front == rear 【空】
• 當頭指針front 小於尾指針rear時，說明佇列不爲空，此時可以出佇列。如若front>=rear，則表示佇列爲空。

public class ArrayQueue {
    public static void main(String[] args) {
       Queue q= new Queue(3);
        char key=' ';
        Scanner sc=new Scanner(System.in);
        while (true){
            System.out.print("s(show):顯示佇列");
            System.out.print("a(add):新增佇列");
            System.out.print("g(get):取出數據");
            System.out.print("h(head):檢視佇列頭部");
            System.out.print("e(eixt):退出程式");
            key=sc.next().charAt(0);
            switch (key){
                case 's':
                    q.showQueue();
                    break;
                case 'a':
                    System.out.println("請輸入一個數");
                    int value=sc.nextInt();
                    q.addQueue(value);
                    break;
                case 'g':
                    try {
                        int res=q.getQueue();
                        System.out.println("取出的數據是"+res);
                    }catch (Exception e){
                        System.out.println(e.getMessage());
                    }
                    break;
                 case 'h':
                     try {
                         int head=q.headQueue();
                         System.out.println("頭數據是"+head);
                     }catch (Exception e){
                         System.out.println(e.getMessage());
                     }
                    break;
                case 'e':
                    System.exit(0);
                default:
                    break;

            }
        }
    }
}

class Queue{
    private int maxSize;
    private  int front;
    private  int rear;
    private int[] arr;

    //建立佇列構造器
    public Queue(int arrMaxSize){
        maxSize=arrMaxSize;
        arr=new int[maxSize];
        front=-1;//指向佇列頭部，佇列頭前一個位置
        rear=-1;//指向佇列尾部，佇列尾的位置
    }
    //判斷佇列滿
    public boolean isFull(){
        return rear==maxSize-1;
    }
    //判斷佇列空
    public boolean isEmpty(){
        return front==rear;
    }
    //新增佇列
    public void addQueue(int n){
        if(isFull()){
            System.out.println("佇列已滿，不能新增數據");
            return;
        }
        rear++;
        arr[rear]=n;
    }
    //獲取佇列數據 出佇列
    public int getQueue(){
        if (isEmpty()){
            throw  new RuntimeException("佇列空");
        }
        front++;
        return arr[front];
    }
    //顯示佇列數據
    public void showQueue(){
        if(isEmpty()){
            System.out.println("佇列空");
            return;
        }
        /*for (int i =0; i <arr.length; i++) {
            if(arr[i]!=0){
                System.out.println("arr["+i+"]="+arr[i]);
            }
        }*/
        for (int i =front; i <= rear; i++) {
                System.out.println("arr["+i+"]="+arr[i]);
        }
    }
    //顯示佇列頭數據
    public int headQueue(){
        if(isEmpty()){
            throw new RuntimeException("佇列空，沒有數據");
        }
        return arr[front+1];

    }

}

問題分析並優化

1. 目前陣列使用一次就不能用，無法達到複用的效果；

2. 將這個陣列使用演算法，改進成一個環形的佇列取模：%

具體如下：

4、環形佇列

4.1 陣列模擬環形佇列思路分析

對前面的陣列模擬佇列的優化，充分利用陣列. 因此將陣列看做是一個環形的。(通過取模的方式來實現即可)

分析說明：

• 尾索引的下一個爲頭索引時表示佇列滿，即將佇列容量空出一個作爲約定,
  這個在做判斷佇列滿的時候需要注意 (rear + 1) % maxSize == front 滿]

• rear == front [空]

• 測試示意圖：

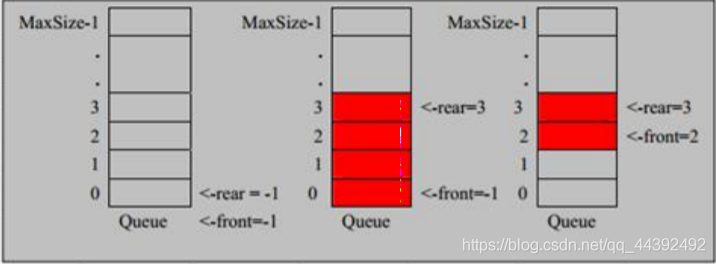
思路如下:

1. front 變數的含義做一個調整： front 就指向佇列的第一個元素, 也就是說 arr[front] 就是佇列的第一個元素 front 的初始值 = 0
2. rear 變數的含義做一個調整：rear 指向佇列的最後一個元素的後一個位置. 因爲希望空出一個空間做爲約定. rear 的初始值 = 0
3. 當佇列滿時，條件是 (rear + 1) % maxSize == front 【滿】
4. 對佇列爲空的條件， rear == front 空
5. 當我們這樣分析， 佇列中有效的數據的個數 (rear + maxSize - front) % maxSize // rear = 1 front = 0
6. 綜上，就可以在原來的佇列上修改得到，一個環形佇列。

4.2 陣列模擬環形佇列及實現

public class CirckeQueue {
    public static void main(String[] args) {
        CircleArray q= new CircleArray(4);//有效數據是3
        char key=' ';
        Scanner sc=new Scanner(System.in);
        while (true){
            System.out.print("s(show):顯示佇列");
            System.out.print("a(add):新增佇列");
            System.out.print("g(get):取出數據");
            System.out.print("h(head):檢視佇列頭部");
            System.out.print("e(eixt):退出程式");
            key=sc.next().charAt(0);
            switch (key){
                case 's':
                    q.showQueue();
                    break;
                case 'a':
                    System.out.println("請輸入一個數");
                    int value=sc.nextInt();
                    q.addQueue(value);
                    break;
                case 'g':
                    try {
                        int res=q.getQueue();
                        System.out.println("取出的數據是"+res);
                    }catch (Exception e){
                        System.out.println(e.getMessage());
                    }
                    break;
                case 'h':
                    try {
                        int head=q.headQueue();
                        System.out.println("頭數據是"+head);
                    }catch (Exception e){
                        System.out.println(e.getMessage());
                    }
                    break;
                case 'e':
                    System.out.println("程式退出");
                    System.exit(0);
                default:
                    break;

            }
        }

    }
}

class CircleArray{
    private int maxSize;
    private  int front; // front 的初始值爲0 front 佇列頭,front 就指向佇列的第一個元素
    private  int rear;//rear 的初始值 = 0 佇列尾,rear指向佇列的最後一個元素的後一個位置
    private int[] arr;


    //建立佇列構造器
    public CircleArray(int arrMaxSize){
        maxSize=arrMaxSize;
        arr=new int[maxSize];
        front=0;//指向佇列頭部，佇列頭的位置
        rear=0;//指向佇列尾部，佇列尾後一個位置
    }
    //判斷佇列滿
    public boolean isFull(){
        return (rear+1)%maxSize==front;
    }
    //判斷佇列空
    public boolean isEmpty(){
        return front==rear;
    }
    //新增佇列
    public void addQueue(int n){
        if(isFull()){
            System.out.println("佇列已滿");
            return;
        }
        arr[rear]=n;//直接加入
        rear=(rear+1)%maxSize;//rear後移需考慮取模
    }
    //獲取佇列數據 出佇列
    public int getQueue(){
        if (isEmpty()){
            throw  new RuntimeException("佇列空");
        }
        int temp=arr[front];
        front=(front+1)%maxSize;
        return temp;
    }
    //顯示佇列數據
    public void showQueue(){
        if(isEmpty()){
            System.out.println("佇列空，沒有數據");
            return;
        }
        for (int i =front; i <front+size(); i++) {
                System.out.println("arr["+i%maxSize+"]="+arr[i % maxSize]);
        }
    }
    //求出佇列有效數據
    public int size(){
        return (rear+maxSize-front)%maxSize;
    }
    //顯示佇列頭數據
    public int headQueue(){
        if(isEmpty()){
            throw new RuntimeException("佇列空.....");
        }
        return arr[front];

    }

}