使用自定義的棧來優化二元樹的遍歷

本文是上一篇文章的後續,詳情點選該鏈接~

前言

       在前面遍歷二元樹的操作裡,基本上都是使用遞回實現的,因爲遞回解決問題的方式會相對回圈來說要更加簡單一些。但是我們要知道,對於計算機而言,卻未必如此。

遞回的缺點

       遞回的優點,想必在之前也已經體會到了。使用遞回解決問題,往往思路清晰,簡單易懂。但是我們要知道,遞回在呼叫的時候會佔用大量的系統堆疊,記憶體耗用非常的多。在遞回呼叫層次多的時候,速度也要比回圈慢得多。所以說,在要求高效能的情況下儘量避免使用遞回，遞回呼叫既花時間又耗記憶體。

優化方案

       我們可以由使用者自己定義一個棧來代替系統棧,也就是用非遞回的方式來實現遍歷演算法，這樣一來可以得到不小的效率提升。

       那麼問題來了。一個是系統棧，而另一個是使用者定義的棧。明明都是棧,爲什麼使用者定義的棧會比系統的棧更高效?

       這裏的一個解釋是遞回函數所申請的系統棧,是一個所有遞回函數都通用的棧。對於二元樹深度優先遍歷演算法。系統棧除了記錄存取過的結點資訊之外,還有其它資訊需要記錄,以實現函數遞回的呼叫。而使用者自己定義的棧,僅儲存了遍歷所需的節點資訊,是對遍歷演算法的一個針對性的設計,對於遍歷演算法來說，顯然要比遞回函數通用的系統棧更高效。

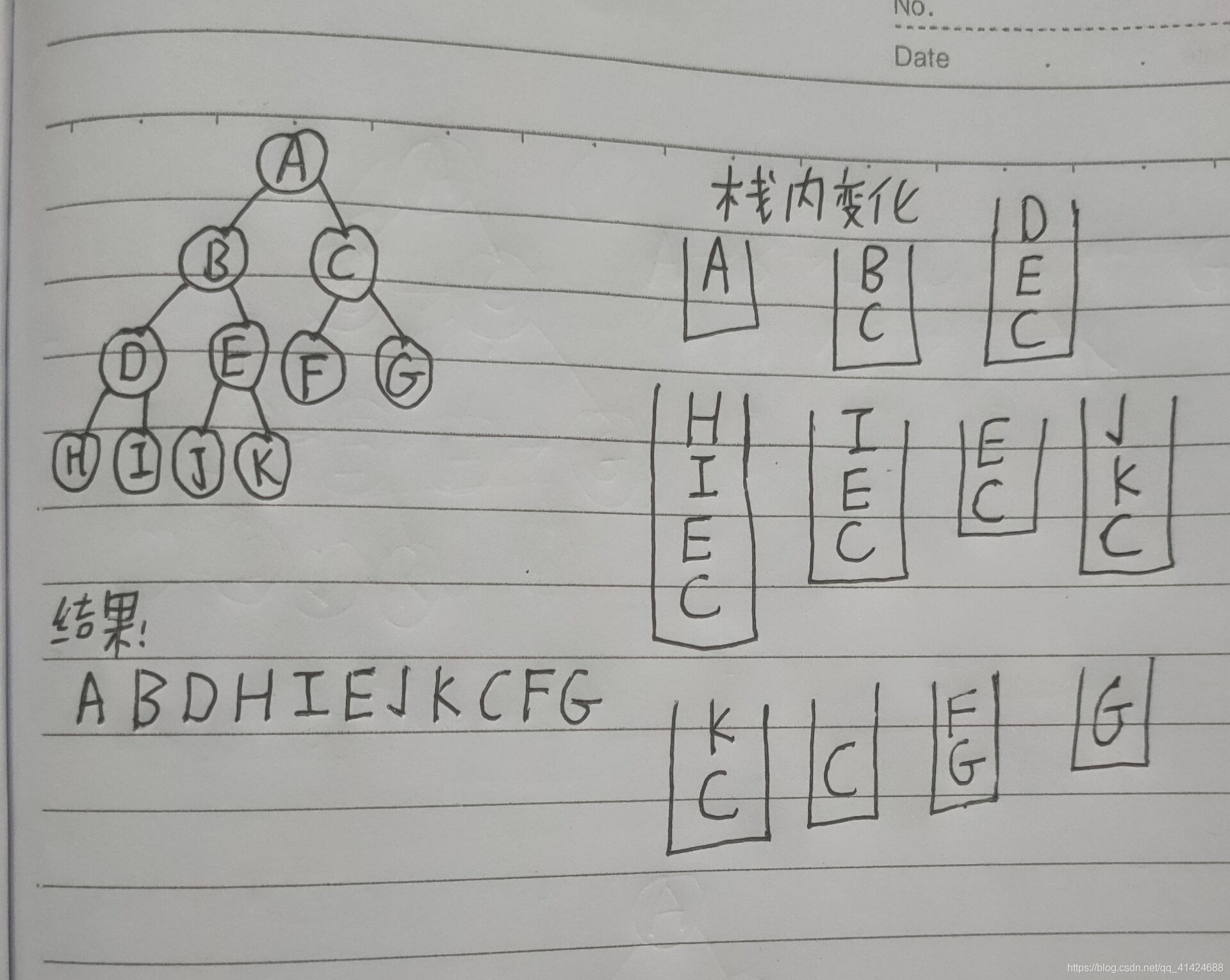
程式碼實現

二元樹的結構還是繼續使用上篇文章開頭圖片上的那棵樹。

先序遍歷

void preOrder(Tree *btn) {
	if (btn != NULL) {
		//定義一個棧
		Tree* Stack[MAXSIZE];
		//初始化棧
		int top = -1;
		Tree* p;
		//根節點入棧
		Stack[++top] = btn;
		//棧空回圈退出,遍歷結束
		while (top != -1) {
			//出棧並輸出棧頂結點
			p = Stack[top--];
			printf("%c ",p->data);
			//棧是先進後出的,所以先讓右孩子進去,再進左孩子
			//等下出來的時候.就是左孩子先出來,右孩子後出來
			//棧頂結點的右孩子存在,則右孩子入棧
			if (p->right != NULL) {
				Stack[++top] = p->right;
			}
			//棧頂結點的左孩子存在,則左孩子入棧
			if (p->left != NULL) {
				Stack[++top] = p->left;
			}
		}
	}
}

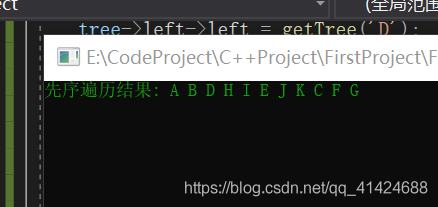
我們看到,執行的結果和剛纔用筆在本子上分析的一樣

---

中序遍歷

       中序遍歷和前序遍歷差不多。遍歷到左孩子最底層之前的結點都會先存入棧內,等遍歷到了左孩子最底層結點之後,纔會開始出棧進棧的過程。

void InOrder(Tree *tree) {
	if (tree != NULL) {
		Tree* Stack[MAXSIZE];
		int top = -1;
		Tree* p;
		p = tree;
		//遍歷
		while (top != -1 || p != NULL) {
			//左孩子入棧
			while (p != NULL) {
				Stack[++top] = p;
				p = p->left;
			}
			//棧不空的時候出棧,並輸出棧結點
			if (top != -1) {
				p = Stack[top--];
				printf("%c ",p->data);
				p = p->right;
			}
		}
	}
}

---

後序遍歷

       在後序遍歷操作之前,我們可以先手動寫上遍歷的結果再進行過程分析

       剛纔的先序遍歷結果爲: A B D H I E J K C F G

       後序遍歷的結果爲: H I D J K E B F G C A

       後序遍歷逆轉的結果:A C G F B E K J D I H

       我們仔細觀察會發現一個規律。就是當我們把後序遍歷的結果倒過來之後就比較像是先序遍歷過程中的左右子樹順序交換後的結果。所以,我們只需要將前面的先序遍歷演算法中的左右子樹順序交換就可以得到逆轉後的後序遍歷序列。然後再把逆轉後的序列逆序也就得到了我們想要的結果。這麼做的話,我們就需要兩個棧。

       一個棧用來輔助做逆後序遍歷,然後將遍歷結果的序列壓入另一個棧當中。由於棧是先進後出的數據結構,所以只需要按照棧的順序把它們正常出棧。就得到我們想要的結果了~

void postOrder(Tree *tree) {
	if (tree != NULL) {
		//定義兩個棧
		Tree* Stack1[MAXSIZE]; int top1 = -1;
		Tree* Stack2[MAXSIZE]; int top2 = -1;
		Tree* p = NULL;
		Stack1[++top1] = tree;
		while (top1 != -1) {
			p = Stack1[top1--];
			Stack2[++top2] = p;
			if (p -> left != NULL) {
				Stack1[++top1] = p->left;
			}
			if (p -> right != NULL) {
				Stack1[++top1] = p->right;
			}
		}
		while (top2 != -1) {
			p = Stack2[top2--];
			printf("%c ",p->data);
		}
	}
}

---

最後奉上完整程式碼

#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 100
typedef struct BinaryNode {
	char data;		//數據域
	struct BinaryNode* left;	//指針域 左孩子
	struct BinaryNode* right;	//指針域 右孩子
}Tree;
//賦值
Tree* getTree(char data) {
	Tree* tree = (Tree*)malloc(sizeof(Tree));
	tree->data = data;
	tree->left = NULL;
	tree->right = NULL;
	return tree;
}
//先序遍歷
void preOrder(Tree* btn) {
	if (btn != NULL) {
		//定義一個棧
		Tree* Stack[MAXSIZE];
		//初始化棧
		int top = -1;
		Tree* p;
		//根節點入棧
		Stack[++top] = btn;
		//棧空回圈退出,遍歷結束
		while (top != -1) {
			//出棧並輸出棧頂結點
			p = Stack[top--];
			printf("%c ", p->data);
			//棧是先進後出的,所以先讓右孩子進去,再進左孩子
			//等下出來的時候.就是左孩子先出來,右孩子後出來
			//棧頂結點的右孩子存在,則右孩子入棧
			if (p->right != NULL) {
				Stack[++top] = p->right;
			}
			//棧頂結點的左孩子存在,則左孩子入棧
			if (p->left != NULL) {
				Stack[++top] = p->left;
			}
		}
	}
}
//中序遍歷
void InOrder(Tree *tree) {
	if (tree != NULL) {
		Tree* Stack[MAXSIZE];
		int top = -1;
		Tree* p;
		p = tree;
		//遍歷
		while (top != -1 || p != NULL) {
			//左孩子入棧
			while (p != NULL) {
				Stack[++top] = p;
				p = p->left;
			}
			//棧不空的時候出棧,並輸出棧結點
			if (top != -1) {
				p = Stack[top--];
				printf("%c ",p->data);
				p = p->right;
			}
		}
	}
}
//後序遍歷
void postOrder(Tree *tree) {
	if (tree != NULL) {
		//定義兩個棧
		Tree* Stack1[MAXSIZE]; int top1 = -1;
		Tree* Stack2[MAXSIZE]; int top2 = -1;
		Tree* p = NULL;
		Stack1[++top1] = tree;
		while (top1 != -1) {
			p = Stack1[top1--];
			Stack2[++top2] = p;
			if (p -> left != NULL) {
				Stack1[++top1] = p->left;
			}
			if (p -> right != NULL) {
				Stack1[++top1] = p->right;
			}
		}
		while (top2 != -1) {
			p = Stack2[top2--];
			printf("%c ",p->data);
		}
	}
}

int main(int argc, char* argv[]) {
	//搭建圖中的二元樹
	Tree* tree = (Tree*)malloc(sizeof(Tree));
	tree = getTree('A');
	tree->left = getTree('B');
	tree->right = getTree('C');
	tree->left->left = getTree('D');
	tree->left->right = getTree('E');
	tree->left->left->left = getTree('H');
	tree->left->left->right = getTree('I');
	tree->left->right->left = getTree('J');
	tree->left->right->right = getTree('K');
	tree->right->left = getTree('F');
	tree->right->right = getTree('G');

	printf("先序遍歷結果: "); preOrder(tree);
	printf("\n\n中序遍歷結果: "); InOrder(tree);
	printf("\n\n後序遍歷結果: "); postOrder(tree);
	getchar();
	return 0;
}