如何簡單生成生成對抗網路 ？

近年來，在人工智慧領域深度學習取得了令人矚目的成就，在計算機視覺、自然語言處理等各種領域都取得了突破性的進展。深度學習現今主要是依靠神經網路模型來進行學習的，可大致分爲三種基礎模型，首先的就是折積神經網路（Convolutional Neural Networks, CNNs，1998）、回圈神經網路（RecurrentNeural Networks, RNNs，2014）、和生成對抗網路（Generative Adversarial Nets, GANs，2014）等。

但由於傳統的深度學習方法需要大量的數據，並且需要大量的先驗知識。鑑於此問題，Ian Goodfellow所提出的生成式對抗網路GAN逐步受到廣大學者的關注。生成對抗網路(GAN)的初始原理十分容易理解，即構造兩個神經網路，一個生成器，一個鑑別器，二者互相競爭訓練，最後達到一種平衡(納什平衡)。GAN 啓發自博弈論中的二人零和博弈（two-player game），GAN 模型中的兩位博弈方分別由生成式模型（generativemodel，G）和判別式模型（discriminative model，D）充當。

生成模型 G 捕捉樣本數據的分佈，用服從某一分佈（均勻分佈，高斯分佈等）的噪聲 z 生成一個類似真實訓練數據的樣本，追求效果是越像真實樣本越好；判別模型 D 是一個二分類器，估計一個樣本來自於訓練數據（而非生成數據）的概率，如果樣本來自於真實的訓練數據，D 輸出大概率，否則，D 輸出小概率。採用對抗訓練機制 機製進行訓練，並使用優化器（如隨機梯度下降（SGD,stochastic gradient descent），自適應時刻估計方法（Adam，AdaptiveMoment Estimation）等）實現優化，二者交替訓練，直到達到納什均衡後停止訓練。

最後，將二者結合起來說，就是訓練判別器D，讓它判斷真假的概率最大化，同時，也訓練生成器G，讓

最小化，總而言之，這是一種二元極小極大博弈問題（minimaxtwo-player game），用一個函數

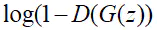
來表示：

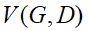
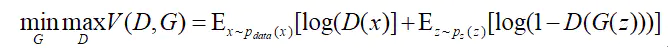
具體的結構如下圖所示：

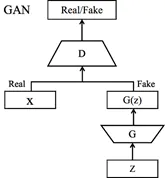
生成式對抗網路模型沒有像傳統的神經網路一樣的損失函數，它使用了關於判別網路模型和生成網路模型的價值函數（Value Function）來表示模型。其中訓練過程爲固定一方（D/G），更新另一個網路的參數，交替迭代，是的對方的錯誤最大化，最後使得生成網路G可以估測出樣本數據的分佈，前文中提到一開始定義了一個生成網路的生成數據的分佈Pg，整個模型希望收斂Pg與樣本數據Pdata的真實分佈，論文中證明了當且僅當Pg=Pdata時存在最優解，即達到納什均衡（納什均衡博弈論中的一個概念，是假設有n個局中人蔘與博弈，如果某情況下無一參與者可以獨自行動而增加收益，即爲了自身利益的最大化，沒有任何單獨的一方願意改變其策略的），此時生成模型G生成了與訓練數據的相同的分佈，判別模型D的準確率等於50%。

總結：本節對抗生成式網路GAN做了一個簡單的介紹，讀者看完之後應該瞭解了生成對抗式網路的原理以及是如何進行work的了。

關注小鯨融創，一起深度學習金融科技！