一、題幹
1.1 題目
投資建模(河北省第三屆研究生建模競賽B題)
從2021年年初開始到2050年前,未來教育基金會(FFE)向M國部分高等院校捐助一筆經費以幫助貧困學生,將現有的8000萬美元資金進行債務投資。
相關投資要求:
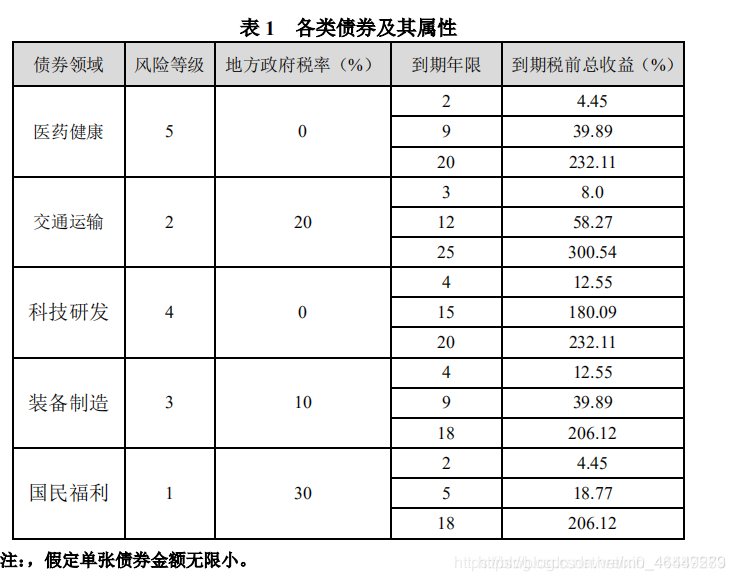
- 醫藥健康債券購買金額不能少於購買總金額的20%,交通運輸、科技研發、裝備製造以及國民福利的債券購買金額不能少於購買總金額的10%。
- 所購買債券的平均風險等級不得低於2.5,等級數位越大,風險越低。
- 所購買的債券的平均到期年限不超過10年。
- 要求捐助活動結束後FFE繼續保留8000萬美元資金。
如上所示爲各個基金的一些資訊,值得注意的是,其對風險等級的約束很小,而收益率又定義爲固定值,所以這個模型相對實際問題已經做了很大的簡化。
1.2 問題
- 若 SEB 債券投資只允許在第一年初進行,分配8000萬美元使收益最大。
- 假定可以進行重複投資,使得 2050 年末的一次性捐款金額達到最大。
- FFE 改變捐助方式,計劃從 2021 開始,在未來 30 年內每年年初捐助一筆每年金額固定的經費。允許重複投資。使得每年捐助的金額達到最大。
- FFE 爲了幫助疫情防控,決定在每年捐助給高校的金額儘量不低於第 3 問 的金額的前提下,投資儘量向醫藥健康和科技研發上傾斜。原則上規定:醫藥健康的投資額,儘量與科技研發相等,儘量是交通運輸的 1.2 倍,儘量是裝備製造 的 1.5 倍,儘量是國民福利的 2 倍。允許重複投資。
二、模型的建立
第一問沒啥寫的價值,直接寫第二、三、四問。
2.1 符號
| 符號 |
意義 |
| money_ini |
第i年在收入狀態後的總資金 |
| money_outi |
第i年在支出狀態後的總資金 |
| xi,j |
第i年對第j個債券的購買量 |
| ai |
第i個產品在一輪週期後的利潤率 |
| bi |
第i個產品一輪週期時常 |
| ci |
第i個產品增值稅率 |
| di |
第i個產品風險等級 |
| p |
每年的捐款數量 |
2.2、思路
2.2.1、思路1
觀察這道題目在投資時的資金流轉過程,可以發現它每年都有這麼兩組操作:
- 繼承一年剩下的資產、獲取前幾年投資所帶來的利潤
- 進行各類債券進行投資、對外捐贈(第三問)
所以我們可以考慮對該問約束時進行狀態分離,即先進行moneyini操作,再進行moneyouti操作。其間的等量關係大致如下,其他的具體情況在正式做的時候再具體討論:
money_ini=money_outi−1+j=1∑15[xi−bi,j+xi−bi,jai(1−ci)]money_ini=money_outi+p+j=1∑15xi,j
2.2.2、思路2
首先根據一個很明顯的構想:如果你當下有錢,且時間足夠充裕到你得到收益,那麼你必然會去拿這筆錢去投資。甭管投啥,反正會投(而投啥其實就是我們要去求解的內容)。因爲如果你今年不投,今後再投的話,在收益上除了時間線的後移外沒有任何變化。所以這裏本質上是一個帶約束的貪心問題。
我們可以粗略的建立一個等量關係,其他的具體情況在正式做的時候再具體討論:
j=1∑15xi,j=j=1∑15[xi−bi,j+xi−bi,jai(1−ci)]
2.3 確定等量關係
思考了上面兩個思路後,發現他們本身其實是並不衝突的,但問題在於以上的貪婪演算法並沒有考慮留每天的捐款的情況。只是表現的形式不一樣。所以可以將他們結合起來,建立如下等量關係。
⎩⎪⎪⎨⎪⎪⎧money_ini=money_outi−1+j=1∑15[xi−bi,j+xi−bi,jai(1−ci)]money_ini=money_outi+p+j=1∑15xi,j
然後基於我們對於題目的分析與各類情況的思考,可以得到以下幾點:
- 當剩餘天數少於該債券週期的話,那麼必然不買這個債券。
- 因爲債券最小週期爲2天,且採用貪心策略,所以前兩天必定是全部花費。(在第三問及第四問中,應留下用於每天捐贈的錢)
- 因爲是貪心策略,所以money_outi只有在最後一天不爲0(該特性爲第二問獨有,第三問與第四問需考慮給捐款存錢的情況)
將其轉化爲符號語言即爲:
⎩⎪⎪⎪⎨⎪⎪⎪⎧j=1∑15i=31−bj∑30xi,j=0j=1∑15x1,j+x2,j=2p
2.4、明確約束
首先根據常識,可以得到如下幾條約束:
⎩⎪⎨⎪⎧xi,j>=0p>=0money_ini>=money_outi>=0
然後根據那四條投資要求,可得出以下四個約束:
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧j=1∑15(bji=1∑30xi,j)≤10j=1∑15i=1∑30xi,jj=1∑15(dji=1∑30xi,j)≥2.5j=1∑15i=1∑30xi,ji=1∑30(xi,1+xi,2+xi,3)>0.2j=1∑15i=1∑30xi,ji=1∑30(xi,3k+xi,3k−1+xk,3j−2)>0.1j=1∑15i=1∑30xi,j,(k∈{2,3,4,5})
暫時想到這些。
三、編寫程式
3.1、第二問
3.2、第三問
3.3、第四問
四、總結
