P4051 [JSOI2007]字元加密 （後綴陣列sa[]）

題意：

喜歡鑽研問題的JS同學，最近又迷上了對加密方法的思考。一天，他突然想出了一種他認爲是終極的加密辦法
：把需要加密的資訊排成一圈，顯然，它們有很多種不同的讀法。例如下圖，可以讀作：

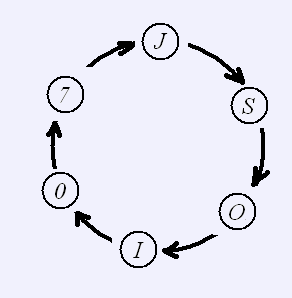
JSOI07 SOI07J OI07JS I07JSO 07JSOI 7JSOI0
把它們按照字串的大小排序：07JSOI 7JSOI0 I07JSO JSOI07 OI07JS SOI07J
讀出最後一列字元：I0O7SJ，就是加密後的字串
（其實這個加密手段實在很容易破解，鑑於這是突然想出來的，那就^^）。
但是，如果想加密的字串實在太長，你能寫一個程式完成這個任務嗎？

數據範圍：字串長度<=1e5

解法：

這道題實際上是在環上對每個點作爲起點的串進行排序,
序列和環容易想到破環成鏈,具體做法就是複製一遍序列接在後面.

題目中的每個串一定都是新串的某個後綴的字首
題目中的n個串就是新串中串[1,n]的後綴的長度爲n的字首
對新串構造後綴陣列,sa[1]到sa[n]就是題目的排序結果
那麼s[sa[i]+n-1]就是末尾字元

ps：
這種方法似乎可以用來求字串的最小表示法（第k小表示法？）

code：

#include<bits/stdc++.h>
using namespace std;
const int maxm=1e5+5;
struct SA{
    static const int N=1e6+5;
    char s[N];
    int sa[N],rk[N],oldrk[N<<1],id[N],px[N],cnt[N];
    int n;
    bool cmp(int x,int y,int w){
        return oldrk[x]==oldrk[y]&&oldrk[x+w]==oldrk[y+w];
    }
    void getSA(){
        int m=300;//字元集大小
        int i,p,w;
        for(i=1;i<=n;i++)cnt[rk[i]=s[i]]++;
        for(i=1;i<=m;i++)cnt[i]+=cnt[i-1];
        for(i=n;i>=1;i--)sa[cnt[rk[i]]--]=i;
        //
        for(w=1;w<n;w<<=1,m=p){
            for(p=0,i=n;i>n-w;i--)id[++p]=i;
            for(i=1;i<=n;i++)if(sa[i]>w)id[++p]=sa[i]-w;
            memset(cnt,0,sizeof cnt);
            for(i=1;i<=n;i++)cnt[px[i]=rk[id[i]]]++;
            for(i=1;i<=m;i++)cnt[i]+=cnt[i-1];
            for(i=n;i>=1;i--)sa[cnt[px[i]]--]=id[i];
            memcpy(oldrk,rk,sizeof rk);
            for(p=0,i=1;i<=n;i++){
                rk[sa[i]]=cmp(sa[i],sa[i-1],w)?p:++p;
            }
        }
        //
//        for(int i=1;i<=n;i++)printf("%d ",sa[i]);
//        puts("");
    }
}sa;
signed main(){
    scanf("%s",sa.s+1);
    sa.n=strlen(sa.s+1);
    //複製
    for(int i=1;i<=sa.n;i++)sa.s[i+sa.n]=sa.s[i];
    sa.n*=2;
    //
    sa.getSA();
    for(int i=1;i<=sa.n;i++){
        if(sa.sa[i]<=sa.n/2){
            printf("%c",sa.s[sa.sa[i]+sa.n/2-1]);
        }
    }
    return 0;
}

---