劍指Offer(上)1-35題實現 python版本
文章目錄
- 1.劍指 Offer03. 陣列中重複的數位
- 2.劍指 Offer 04. 二維陣列中的查詢
- 3.劍指 Offer 05. 替換空格
- 4.劍指 Offer 06. 從尾到頭列印鏈表
- 5.劍指 Offer 07. 重建二元樹
- 6.劍指 Offer09. 用兩個棧實現佇列
- 7.劍指 Offer 10- I. 斐波那契數列
- 8.劍指 Offer 10- II. 青蛙跳臺階問題
- 9.劍指 Offer 11. 旋轉陣列的最小數位
- 10.劍指 Offer 12. 矩陣中的路徑
- *11.劍指 Offer 13. 機器人的運動範圍
- 12.劍指 Offer 14- I. 剪繩子
- 13.劍指 Offer 14- II. 剪繩子 II
- *14.面試題15. 二進制中1的個數
- *15.劍指 Offer 16. 數值的整數次方
- *16.劍指 Offer 17. 列印從1到最大的n位數
- 17.劍指 Offer 18. 刪除鏈表的節點
- 18.劍指 Offer 19. 正則表達式匹配
- 19.劍指 Offer 20. 表示數值的字串
- 20.劍指 Offer 21. 調整陣列順序使奇數位於偶數前面
- 21.劍指 Offer 22. 鏈表中倒數第k個節點
- 22.劍指 Offer 24. 反轉鏈表
- 23.劍指 Offer 25. 合併兩個排序的鏈表
- *24.劍指 Offer 26. 樹的子結構
- 25.劍指 Offer 27. 二元樹的映象
- 26.劍指 Offer 28. 對稱的二元樹
- 27.劍指 Offer 29. 順時針列印矩陣
- 28.劍指 Offer 30. 包含min函數的棧
- 29.劍指 Offer 31. 棧的壓入、彈出序列
- 30.劍指 Offer 32 - I. 從上到下列印二元樹
- 31.劍指 Offer 32 - II. 從上到下列印二元樹 II
- 32.劍指 Offer 32 - III. 從上到下列印二元樹 III
- 33.劍指 Offer 33. 二元搜尋樹的後序遍歷序列
- 34.劍指 Offer 34. 二元樹中和爲某一值的路徑
- 35.劍指 Offer 35. 複雜鏈表的複製
1.劍指 Offer03. 陣列中重複的數位
構造雜湊表,或者用陣列位置記錄,如果大於1,則有重複。
(1)小偷懶,用Python內部函數實現:
class Solution:
def findRepeatNumber(self, nums: List[int]) -> int:
res=collections.Counter(nums)
for key in res:
if res[key]>1:
return key
(2)構造雜湊
class Solution:
def findRepeatNumber(self, nums: List[int]) -> int:
res={}
for ch in nums:
if ch not in res:
res[ch]=1
else:
return ch
2.劍指 Offer 04. 二維陣列中的查詢

找到這個二維陣列的特點
class Solution:
def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
if not matrix:
return False
#從右上角開始,大於該數向下走,小於向左走
n=len(matrix)
m=len(matrix[0])
i,j=0,m-1
while 0<=i<n and 0<=j<m:
if matrix[i][j]==target:
return True
elif matrix[i][j]<target:
i+=1
else:
j-=1
return False
3.劍指 Offer 05. 替換空格

其實就是把佔位一個字元的空格替換爲佔位三個字元的%20.
要注意使用python語言時,字串是一個不可變陣列,所以最好新建一個list,在list中進行操作。
class Solution:
def replaceSpace(self, s: str) -> str:
res=[]
for ch in s:
if ch==' ':
res.append("%20")
else:
res.append(ch)
return "".join(res)
4.劍指 Offer 06. 從尾到頭列印鏈表

用一個棧來輔助
class Solution:
def reversePrint(self, head: ListNode) -> List[int]:
res=[]
while head:
res.append(head.val)
head=head.next
return res[::-1]
5.劍指 Offer 07. 重建二元樹
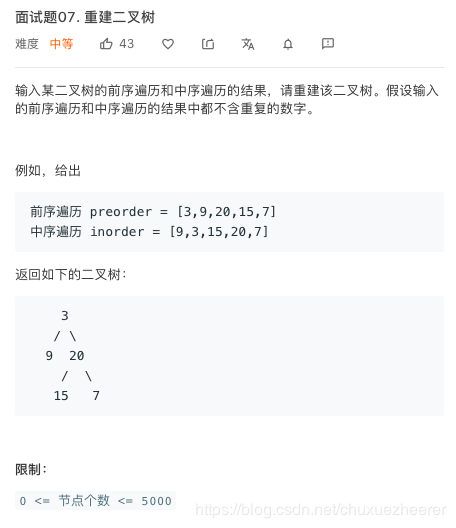
前序遍歷:根左右。中序遍歷:左根右。
遞回思想,前序遍歷中pre_left爲結點的根,之後在中序遍歷中尋找,獲得值爲pre_left的下標位置,左邊的爲左子樹,右邊的是右子樹。
遞回,從前序中獲得根節點位置,從中序中獲得子樹長度。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
#前序:根左右
#中序:左根右
self.preRootDict={}
self.pre=preorder
for i in range(len(inorder)):
self.preRootDict[inorder[i]]=i #記錄中序結點的位置
return self.getRoot(0,0,len(inorder)-1)#根結點,中序遍歷範圍
def getRoot(self,preRoot,inorderLeft,inorderRight):
if inorderLeft>inorderRight: #中序遍歷爲空
return
root=TreeNode(self.pre[preRoot]) #建立根結點
i=self.preRootDict[self.pre[preRoot]] #找到前序中根結點在中序中的位置
root.left=self.getRoot(preRoot+1,inorderLeft,i-1)
#preRoot當前的根 左子樹的長度 = 左子樹的右邊-左邊 (i-1-inorderLeft+1) 。最後+1就是右子樹的根了
root.right=self.getRoot(preRoot+i-inorderLeft+1,i+1,inorderRight)
return root
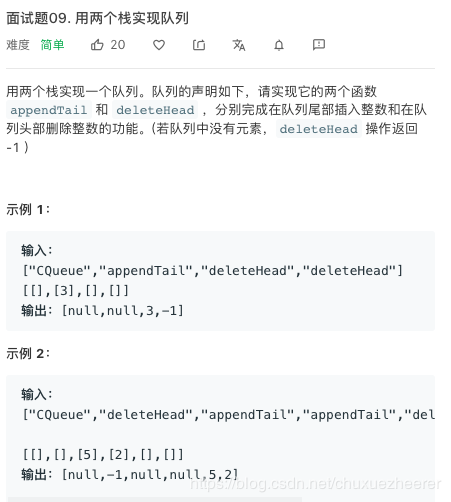
6.劍指 Offer09. 用兩個棧實現佇列
class CQueue:
def __init__(self):
self.stack1=[]
self.stack2=[]
def appendTail(self, value: int) -> None:
self.stack1.append(value)
def deleteHead(self) -> int:
if self.stack2:
return self.stack2.pop()
else:
if self.stack1:
while self.stack1:
self.stack2.append(self.stack1.pop())
return self.stack2.pop()
else:
return -1
7.劍指 Offer 10- I. 斐波那契數列
這一看就是動態陣列問題。但常規的F(n)=F(n-1)+F(n-2)這種方法輸入會超時。所以用一個輔助的字典記錄已經算過的值。
class Solution:
def fib(self, n: int) -> int:
if n<=0:
return 0
arr={}
return self.fibNum(arr,n)%1000000007
def fibNum(self,arr,n):
if n==1 or n==2:
return 1
if n in arr:
return arr[n] #記錄以前已經算過的值,若已經存在則直接返回。
arr[n]=self.fibNum(arr,n-1)+self.fibNum(arr,n-2)
return arr[n]
還有一種方法,相對簡單。
class Solution:
def fib(self, n: int) -> int:
a, b = 0, 1
for _ in range(n):
a, b = b, a + b
return a % 1000000007
差不多 …(甩鍋給leetcode…)
8.劍指 Offer 10- II. 青蛙跳臺階問題
解題思路同上道題,第n個臺階,不是從n-1個臺階上來就是從n-2個臺階上來。
class Solution:
def numWays(self, n: int) -> int:
if n<=0:
return 1
arr={}
return (self.f(arr,n))%1000000007
def f(self,arr,n):
if n==1:
return 1
elif n==2:
return 2
if n in arr:
return arr[n]
arr[n]=self.f(arr,n-1)+self.f(arr,n-2)
return arr[n]
9.劍指 Offer 11. 旋轉陣列的最小數位
借鑑:某位大佬寫的更加詳細
二分法的思想
class Solution:
def minArray(self, numbers: [int]) -> int:
i, j = 0, len(numbers) - 1
while i < j:
m = (i + j) // 2 #中心點
if numbers[m] > numbers[j]: i = m + 1 #若右側的點小於中心位置的點,則說明旋轉點在中心位置的右側
elif numbers[m] < numbers[j]: j = m #若右側的點大於中心位置的點,則說明旋轉點在中心位置的左側
else: j -= 1 #若相等,則情況不明需要進一步判斷(比如01011111和123123兩種旋轉點不一樣)
return numbers[i]
10.劍指 Offer 12. 矩陣中的路徑

這道題利用深度優先遍歷+回溯思想。
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
def dfs(i,j,k):
if not 0<=i<len(board) or not 0<=j<len(board[0]) or board[i][j]!=word[k]:
return False
if k==len(word)-1:
return True
#用一個臨時值儲存當前值,用於回溯
tmp,board[i][j]=board[i][j],'/'
#進行深度遍歷
res=dfs(i+1,j,k+1) or dfs(i-1,j,k+1) or dfs(i,j+1,k+1) or dfs(i,j-1,k+1)
board[i][j]=tmp
return res
for i in range(len(board)):
for j in range(len(board[0])):
if dfs(i,j,0):
return True
return False

*11.劍指 Offer 13. 機器人的運動範圍
BFS遍歷
class Solution:
#計算當前方格的各個位上的和
def getSum(self,row,col):
tmp=0
while row>0:
tmp+=row%10
row=row//10
while col>0:
tmp+=col%10
col=col//10
return tmp
def movingCount(self, m: int, n: int, k: int) -> int:
#BFS
road=set() #將走過的路徑新增到集閤中
queue=collections.deque()
queue.append((0,0))
while (queue):
i,j=queue.pop()
if (i,j) not in road and self.getSum(i,j)<=k:
road.add((i,j))
for di,dj in [(1,0),(0,1)]: #僅考慮往右往下就可
if 0<=(i+di)<m and 0<=(j+dj)<n:
queue.append((i+di,j+dj))
return (len(road))
DFS程式碼:
class Solution:
#計算當前方格的各個位上的和
def getSum(self,row,col):
tmp=0
while row>0:
tmp+=row%10
row=row//10
while col>0:
tmp+=col%10
col=col//10
return tmp
def movingCount(self, m: int, n: int, k: int) -> int:
def dfs(i,j):
if i>=m or j>=n or (i,j) in road or self.getSum(i,j)>k:
return
road.add((i,j)) #加入路徑中
dfs(i+1,j) #遞回呼叫
dfs(i,j+1)
road=set()
dfs(0,0)
return (len(road))
12.劍指 Offer 14- I. 剪繩子
運用動態規劃思路,狀態轉移方程:
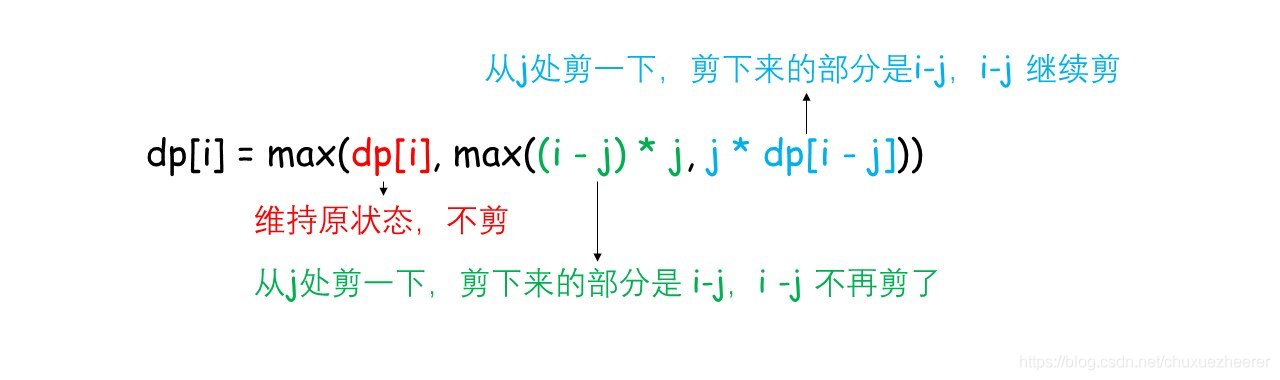
邊界值,dp[1]=dp[2]=1,表示長度爲2的繩子最大乘積爲1
class Solution:
def cuttingRope(self, n: int) -> int:
dp=[0 for _ in range(n+1)]
#初始化
dp[2]=1
#記錄結果
res=-1
for i in range(3,n+1):
for j in range(i):
dp[i]=max(dp[i],max((i-j)*j,j*dp[i-j]))
return dp[n]
13.劍指 Offer 14- II. 剪繩子 II

參考:
https://leetcode-cn.com/problems/jian-sheng-zi-ii-lcof/solution/mian-shi-ti-14-ii-jian-sheng-zi-iitan-xin-er-fen-f/
和上一道題做對比,這裏運用一個數學推導:儘可能將繩子以長度 3 等分爲多段時,乘積最大。
class Solution:
def cuttingRope(self, n: int) -> int:
if n==2:
return 1
if n==3:
return 2
if n%3==0: #能整除3
return (3**(n//3)%int(1e9+7))
elif n%3==1: #餘數爲1,最後一步 *4>*3*1,所以分成先-4
return (3**((n-4)//3)*4%int(1e9+7))
else: #餘數爲2,最後一步 *2*3>*5,所以只-2,不是-5
return (3**((n-2)//3)*2%int(1e9+7))

*14.面試題15. 二進制中1的個數
這是一道位運算的題。這裏有一個基礎知識 n&(n-1)會把最後一個1消去。
(借鑑大佬的圖),所以每做一次這種操作相當於減少一個1.

class Solution:
def hammingWeight(self, n: int) -> int:
res=0
while n!=0:
res+=1
n=n&(n-1)
return res
*15.劍指 Offer 16. 數值的整數次方

首先看書上寫,面試官考這道題的目的主要是想考察情況是否考慮完全了(負數、0)。
然後解題思路這裏借鑑這位大佬寫的:
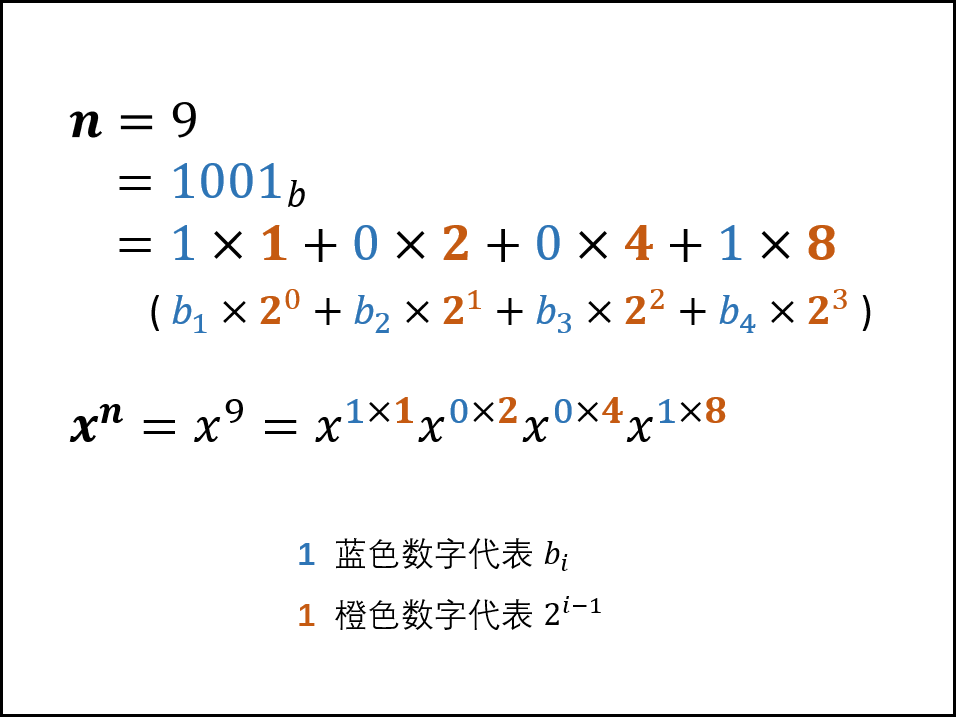
演算法流程:
1.當 x=0 時:直接返回 0 (避免後續 x=1/x 操作報錯)。
2.初始化 res=1 ;
3.當 n<0 時:把問題轉化至 n≥0 的範圍內,即執行x=1/x,n=-n
4.回圈計算:當 n=0 時跳出; (1)當 n&1=1 時:將當前 x 乘入 res (即 res∗=x ); (2)執行 x=x^2(即 x∗=x ); (3)執行 n 右移一位(即 n>>=1)。
5.返回 res 。
class Solution:
def myPow(self, x: float, n: int) -> float:
if n<0:
x=1/x
n=-n
res=1
while n:
if n&1:
res*=x
x*=x
n>>=1
return res
*16.劍指 Offer 17. 列印從1到最大的n位數

這道題如果用Python寫,可以直接回圈出結果:
class Solution:
def printNumbers(self, n: int) -> List[int]:
res = []
for i in range(1, 10 ** n):
res.append(i)
return res
但這裏要學習的是大數列印的思想,將數位轉換成字串進行列印:
首先是全排列:
class Solution:
def printNumbers(self, n: int) -> [int]:
def dfs(x):
if x == n: # 終止條件:已固定完所有位
res.append(''.join(num)) # 拼接 num 並新增至 res 尾部
return
for i in range(10): # 遍歷 0 - 9
num[x] = str(i) # 固定第 x 位爲 i
dfs(x + 1) # 開啓固定第 x + 1 位
num = ['0'] * n # 起始數位定義爲 n 個 0 組成的字元列表
res = [] # 數位字串列表
dfs(0) # 開啓全排列遞回
return ','.join(res) # 拼接所有數位字串,使用逗號隔開,並返回
這個的執行結果爲:前面的0都沒有去掉

改進:
class Solution:
def printNumbers(self, n: int) -> List[int]:
def dfs(x):
if x==n:
s=''.join(num[self.start:]) #跳出條件,結果不記錄前面的0前導
if s!='0':
res.append(int(s)) #轉化成int型記錄進去
if n-self.start==self.nine: #和9的個數相比較
self.start-=1
return
for i in range(10): #開始全排列
if i==9:
self.nine+=1
num[x]=str(i)
dfs(x+1)
self.nine-=1
num,res=['0']*n,[]
self.nine=0
self.start=n-1
dfs(0)
return res
17.劍指 Offer 18. 刪除鏈表的節點

這道題作爲常規題挺簡單的,如下解法,需要用到兩個指針,一個p指針作爲每次移動,判斷val值的內容,還有一個指針指向p前一個結點,準備刪除p用。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def deleteNode(self, head: ListNode, val: int) -> ListNode:
if head.val==val:
head=head.next #判斷若頭節點就是所找的數值
front=head
p=head.next
while(p):
if p.val==val:
front.next=p.next
front=front.next
p=p.next
return head
:但劍指offer上的意思,val處的值型別是ListNode,跟這裏還有些不同,且要求時間複雜度要爲O(1)。
刪除方法:找到待刪除節點的下一個結點,把下一個結點的內容複製到需要刪除的結點上覆蓋原有的內容,再把下一個結點刪除。
要考慮頭節點和尾結點的情況。尾結點的話需要重新遍歷鏈表,用老方法刪除。
這個方法leetcode上沒發運行,因爲結點型別不同。
class Solution:
def deleteNode(self, head, val):
if head is None or val is None:
return None
if val.next is not None: # 待刪除節點不是尾節點
tmp = val.next #找到下一個結點
val.val = tmp.val
val.next = tmp.next #這兩步,把下一個結點的內容覆蓋當前結點。
elif head == val: # 待刪除節點只有一個節點,此節點爲頭節點
head = None
else:
cur = head # 若待刪除節點爲尾節點
while cur.next != val:
cur = cur.next
cur.next = None
return head
18.劍指 Offer 19. 正則表達式匹配

這也能用動態規劃思想…借鑑大佬的思路:

class Solution:
def isMatch(self, s: str, p: str) -> bool:
m,n=len(s),len(p)
dp=[[False]*(n+1) for _ in range(m+1)]
for i in range(m+1):
for j in range(n+1):
#分成空正則和非空正則
if (j==0):
dp[i][j]=i==0
else:
#非空正則分爲*和不是*的情況
if(p[j-1]!='*'):
if(i>0 and (s[i-1]==p[j-1] or p[j-1]=='.')):#情況一和情況二
dp[i][j]=dp[i-1][j-1]
else:
#該位置上是*了,分爲看和不看兩種情況
#不看
if(j>=2):
dp[i][j]|=dp[i][j-2]
#看
if(i>=1 and j>=2 and (s[i-1]==p[j-2] or p[j-2]=='.')):
dp[i][j]|=dp[i-1][j]
return dp[m][n]
注:第三種情況裡,分爲看和不看兩種,對於這兩種情況,我們都要算,當然是希望儘可能的爲true,而且一種情況算出來的true不會被另外一種情況的false抹掉,所有用|=
19.劍指 Offer 20. 表示數值的字串

本題應用狀態機,主要是弄清楚每個狀態
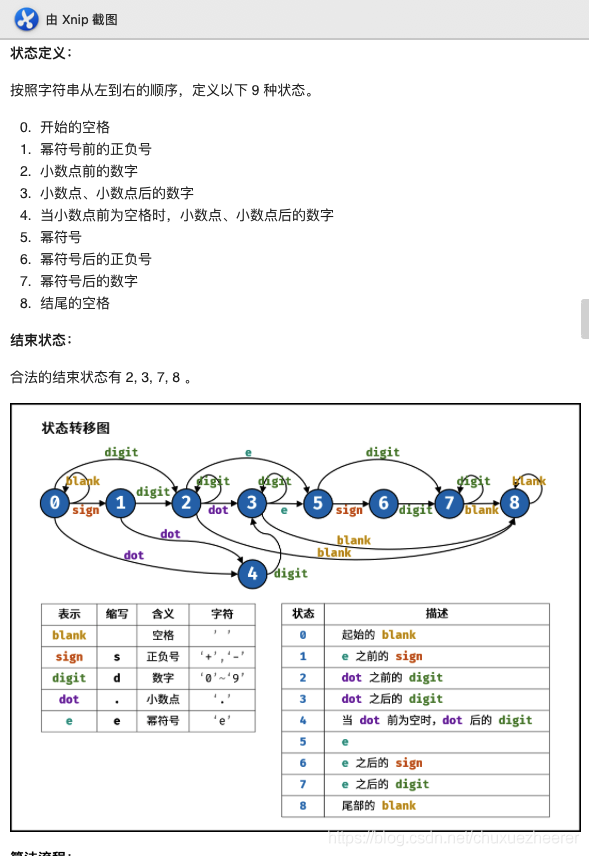
class Solution:
def isNumber(self, s: str) -> bool:
states = [
{' ':0,'s': 1,'d': 2,'.': 4 }, # 0. start with 'blank'
{ 'd':2,'.': 4 },# 1. 'sign' before 'e'
{ 'd':2,'.':3,'e':5,' ':8 }, # 2. 'digit' before 'dot'
{ 'd':3,'e':5,' ':8 },# 3. 'digit' after 'dot'
{ 'd':3},# 4. 'digit' after 'dot' (‘blank’ before 'dot')
{ 's':6,'d':7}, # 5. 'e'
{ 'd':7}, # 6. 'sign' after 'e'
{ 'd':7,' ':8 },# 7. 'digit' after 'e'
{ ' ': 8 } # 8. end with 'blank'
]
p=0
for c in s:
if '0'<=c<='9':
t='d'
elif c in "+-":
t='s'
elif c in ".eE ": #dot,e,E,space
t=c #符號本身表示字元型別
else:
t='?'
if t not in states[p]:
return False
p=states[p][t]
return p in (2,3,7,8)

20.劍指 Offer 21. 調整陣列順序使奇數位於偶數前面
看到這個就想到了用快排的思想
class Solution:
def exchange(self, nums: List[int]) -> List[int]:
left=0
right=len(nums)-1
while left<right:
while left<right and nums[left]%2!=0:
left+=1
while left<right and nums[right]%2==0:
right-=1
nums[left],nums[right]=nums[right],nums[left]
return nums
21.劍指 Offer 22. 鏈表中倒數第k個節點
這道題本身沒有什麼難的,用快慢指針就可以實現。快指針先走K步,然後快慢指針同時走, 快指針到達終點時,慢指針即爲所求。
但要注意的是程式碼的魯棒性,即三個需要考慮能使系統崩潰的點:
1.head爲空指針;
2.k大於鏈表的長度;
3.輸入的參數k爲0;
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getKthFromEnd(self, head: ListNode, k: int) -> ListNode:
if not head or k==0: #要考慮如果頭節點是空或者k=0沒有意義的情況
return None
quick=head
slow=head
while k:
if quick: #要考慮如果k大於整個鏈的長度
quick=quick.next
k-=1
else:
return None
while quick:
quick=quick.next
slow=slow.next
return slow
22.劍指 Offer 24. 反轉鏈表
方法一:用棧實現:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if not head:
return None
queue=[]
while head.next:
queue.append(head)
head=head.next
temp=head
while queue:
node=queue.pop()
temp.next=node
temp=node
temp.next=None
return head
方法二:用兩個指針輔助,原鏈表逆置
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if not head:
return None
pre=head.next
q=head.next
head.next=None
while q:
q=q.next
pre.next=head
head=pre
pre=q
return head
23.劍指 Offer 25. 合併兩個排序的鏈表
常規題,新建立一個結點,然後加入兩個鏈表中較小的結點。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
new_node=cur=ListNode(0)
while l1 and l2:
if l1.val<l2.val:
cur.next=l1
l1=l1.next
cur=cur.next
else:
cur.next=l2
l2=l2.next
cur=cur.next
if l1:
cur.next=l1
elif l2:
cur.next=l2
return new_node.next
上面的解法要新建了結點,如果題目要求不能新建結點,只能在原有鏈表上改動呢?
如下解法:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
if not l1:
return l2
if not l2:
return l1 #考慮兩個空字串
if l1.val>l2.val:
l1,l2=l2,l1 #保證l1的頭節點是兩個中較小的
p=l1
q=l2
while p and q:
if p.val<=q.val and (p.next==None or p.next.val>=q.val):#插入條件
l2=l2.next
q.next=p.next
p.next=q
p=q
q=l2
else:
p=p.next
if l2:#如果l2有剩下的
p=l1
while p.next!=None:
p=p.next
p.next=l2
return l1
方法三:還有遞回演算法
class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
if not l1:
return l2
if not l2:
return l1
if l1.val < l2.val:
l1.next = self.mergeTwoLists(l1.next, l2)
return l1
l2.next = self.mergeTwoLists(l1, l2.next)
return l2
*24.劍指 Offer 26. 樹的子結構
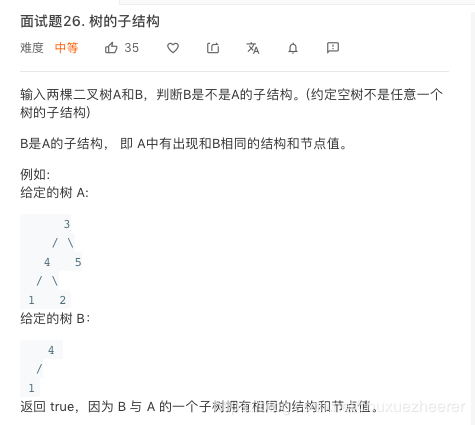
利用遞回實現先序遍歷然後比較
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
if A==None or B==None:
return False
return self.dfs(A,B) or self.isSubStructure(A.left,B) or self.isSubStructure(A.right,B)
def dfs(self,A,B):
if B==None:
return True
if A==None:
return False
return A.val==B.val and self.dfs(A.left,B.left) and self.dfs(A.right,B.right)
借鑑大佬的圖:
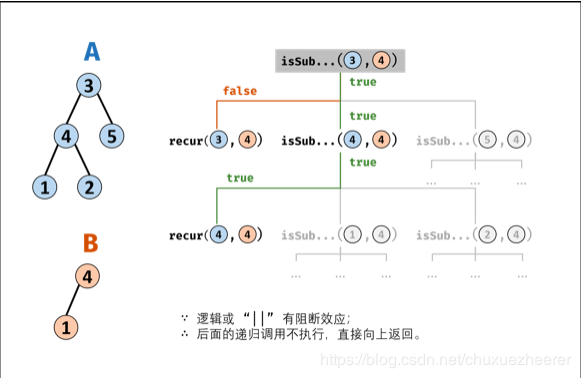
25.劍指 Offer 27. 二元樹的映象

用遞回來做,交換左右子樹,當到頭時返回None狀態。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
if root.left!=None or root.right!=None:
root.left,root.right=root.right,root.left
self.mirrorTree(root.left)
self.mirrorTree(root.right)
return root
方法二:用棧輔助
將結點出棧,然後將該結點的左右子樹入棧,交換左右子樹。直到棧爲空時結束。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
stack=[]
if not root:
return
stack.append(root)
while stack:
cur_root=stack.pop()
if cur_root.left:
stack.append(cur_root.left)
if cur_root.right:
stack.append(cur_root.right)
cur_root.left,cur_root.right=cur_root.right,cur_root.left
return root
26.劍指 Offer 28. 對稱的二元樹
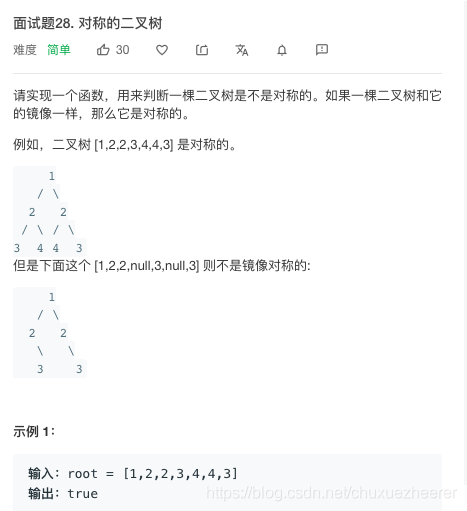
運用遞回的方法。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
def help(left,right):
#左右兩邊都沒有結點了,跳出條件之一
if not left and not right:
return True
#左沒有結點或者右沒有結點或者兩個值不相等,跳出條件之二
if not left or not right or left.val!=right.val:
return False
#剩下的繼續遞回
return help(left.left,right.right) and help(left.right,right.left)
return help(root.left,root.right) if root else True
方法二,迭代法,利用樹的層序遍歷
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue=collections.deque()
queue.appendleft(root.left)
queue.append(root.right)
while queue:
left_node=queue.popleft()
right_node=queue.pop()
#判斷條件
if not left_node and not right_node:
continue
if not left_node or not right_node or left_node.val!=right_node.val:
return False
queue.appendleft(left_node.right)
queue.appendleft(left_node.left)
queue.append(right_node.left)
queue.append(right_node.right)
return True

27.劍指 Offer 29. 順時針列印矩陣
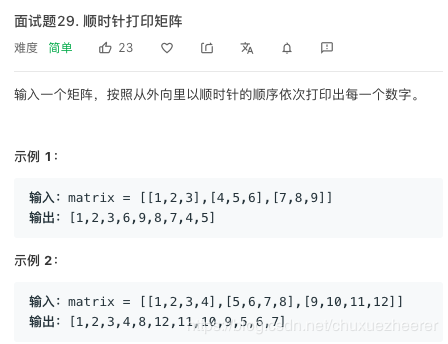
借鑑大佬的思路,左上角的值爲原點(0,0),向右向下增加。
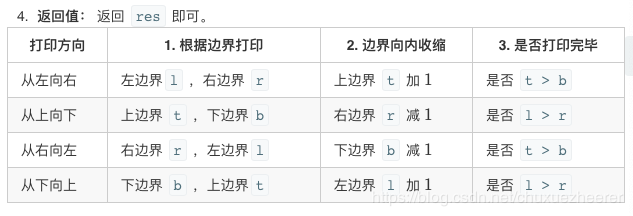
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix:
return matrix
top=0
bottom=len(matrix)-1
left=0
right=len(matrix[0])-1
res=[]
while True:
#從左向右遍歷
for i in range(left,right+1):
res.append(matrix[top][i])
top+=1
if top>bottom:
break
#從上到下
for j in range(top,bottom+1):
res.append(matrix[j][right])
right-=1
if right<left:
break
#從右到左
for i in range(right,left-1,-1):
res.append(matrix[bottom][i])
bottom-=1
if top>bottom:
break
#從下到上
for j in range(bottom,top-1,-1):
res.append(matrix[j][left])
left+=1
if left>right:
break
return res
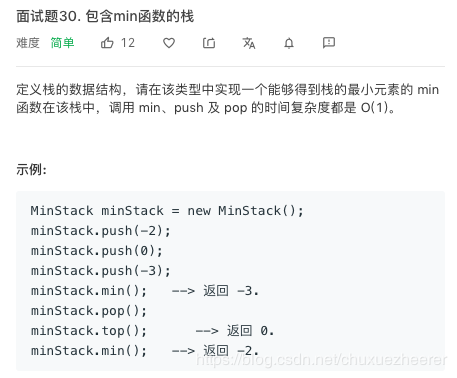
28.劍指 Offer 30. 包含min函數的棧
class MinStack:
def __init__(self):
self.A, self.B = [], []
def push(self, x: int) -> None:
self.A.append(x)
if not self.B or self.B[-1] >= x:
self.B.append(x)
def pop(self) -> None:
if self.A.pop() == self.B[-1]:
self.B.pop()
def top(self) -> int:
return self.A[-1]
def min(self) -> int:
return self.B[-1]
29.劍指 Offer 31. 棧的壓入、彈出序列

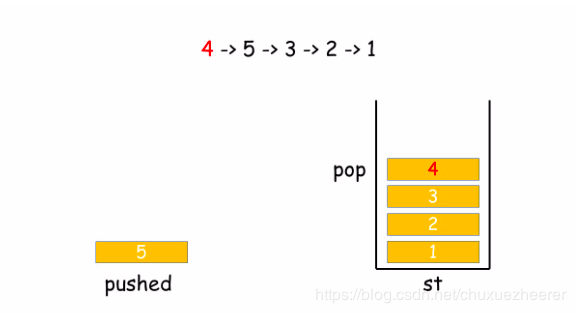
在用一個輔助棧來模擬popped的輸出規則,如果輔助棧頂等於popped的頭,那麼輔助棧出棧,如果最後輔助棧爲空,則popped序列成立。
例如:
class Solution:
def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:
stack=[]
j=0
for num in pushed:
stack.append(num)
while stack and stack[-1]==popped[j]:
stack.pop()
j+=1
if not stack:
return True
return False
30.劍指 Offer 32 - I. 從上到下列印二元樹

沒啥說的,就是一個很簡單的層序遍歷!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[int]:
queue=collections.deque()
res=[]
if not root:
return []
queue.append(root)
while (queue):
node=queue.popleft()
res.append(node.val)
if (node.left):
queue.append(node.left)
if(node.right):
queue.append(node.right)
return res
31.劍指 Offer 32 - II. 從上到下列印二元樹 II
傳統的層次遍歷
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
queue=collections.deque()#記錄結點
queue.append(root)#首先將根節點入棧
res=[]#最後的結果值
while queue:
line=[]#每一行的值
for _ in range(len(queue)):
node=queue.popleft()
line.append(node.val)#結點出佇列,進入結果棧
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right) #左右孩子入佇列
res.append(line)
return res
同102. 二元樹的層序遍歷
這裏應用另一種遞回的方法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
res=[]
def helper(node,level):
if len(res)==level:
res.append([])
res[level].append(node.val)
if node.left:
helper(node.left,level+1)
if node.right:
helper(node.right,level+1)
helper(root,0)
return res
32.劍指 Offer 32 - III. 從上到下列印二元樹 III

進階版的層序遍歷。分奇數層偶數層來進行。這裏要注意兩點,第一個是如可判斷奇偶層——這裏是通過數res裡陣列個數來實現的,第二是如何判斷這一層有多少元素——在操作開始前數一下deque裡的元素個數。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
res=[]
deque=collections.deque()
deque.append(root)
while (deque):
tmp=collections.deque()
for i in range(len(deque)): #這一層元素個數
node=deque.popleft()
if (len(res)%2):#奇數層,從佇列頭部增加
tmp.appendleft(node.val)
else:
tmp.append(node.val)#偶數層,從佇列尾增加
if (node.left):
deque.append(node.left)
if(node.right):
deque.append(node.right)
res.append(list(tmp))
return res
33.劍指 Offer 33. 二元搜尋樹的後序遍歷序列

後序遍歷左右根,運用遞回思想
class Solution:
def verifyPostorder(self, postorder: List[int]) -> bool:
i=0
j=len(postorder)-1
return self.veriftyRes(postorder,i,j)
def veriftyRes(self,porder,i,j):
if i>=j:
return True
left=i
while porder[left]<porder[j]:
left+=1
right=left #劃分左右子樹,right位置爲右子樹起點
while porder[left]>porder[j]:
left+=1
return left==j and self.veriftyRes(porder,i,right-1) and self.veriftyRes(porder,right,j-1)
34.劍指 Offer 34. 二元樹中和爲某一值的路徑

先序遍歷,在遍歷中儲存結果。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
res=[]#最後的結果
path=[]#遍歷的路徑
def preOrder(root,cur_sum):
if not root:
return
path.append(root.val)
cur_sum-=root.val
if cur_sum==0 and not root.left and not root.right:
res.append(list(path))
preOrder(root.left,cur_sum)
preOrder(root.right,cur_sum)
path.pop()
preOrder(root,sum)
return res
35.劍指 Offer 35. 複雜鏈表的複製
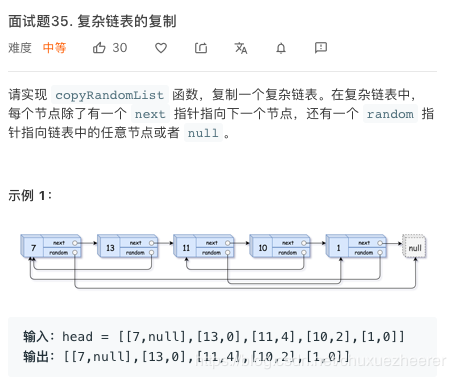
本題題意是要進行深拷貝。
參考程式碼
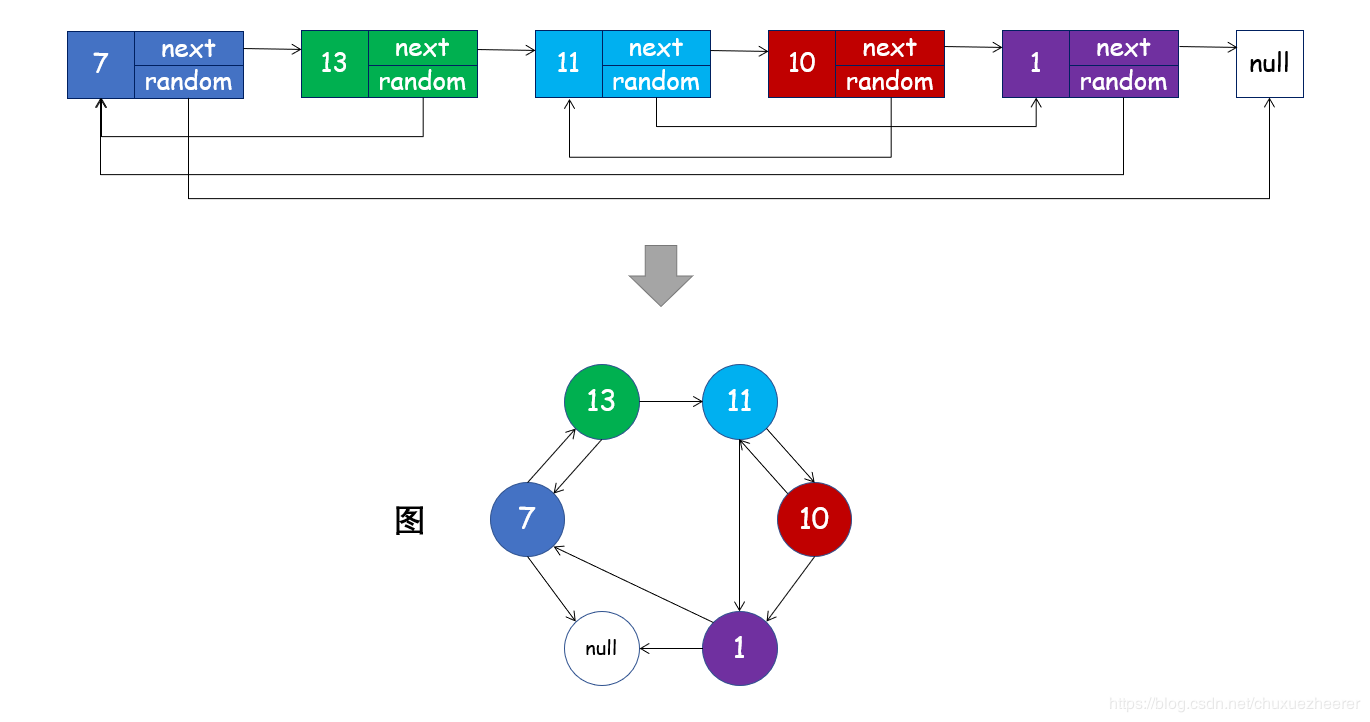
可以將此鏈表看成一個圖
方法一:深度優先搜尋
"""
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
"""
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
def dfs(head):
if not head:
return None
if head in visited:
return visited[head]
copy=Node(head.val,None,None)
visited[head]=copy
#先複製next結點:
copy.next=dfs(head.next)
#再複製random結點:
copy.random=dfs(head.random)
return copy
visited={}
return dfs(head)
方法二:廣度優先搜尋
1.建立雜湊表儲存已拷貝結點,格式 {原結點:拷貝結點}
2.建立佇列,並將頭結點入隊;
3.當佇列不爲空時,彈出一個結點,如果該結點的 next 結點未被拷貝過,則拷貝 next 結點並加入佇列;同理,如果該結點的 random 結點未被拷貝過,則拷貝 random 結點並加入佇列;
"""
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
"""
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
visited={}
def bfs(head):
if not head:
return head
#建立新的結點
copy=Node(head.val,None,None)
#利用佇列記錄
queue=collections.deque()
queue.append(head)
visited[head]=copy
while queue:
node=queue.pop()
if node.next and node.next not in visited:
visited[node.next]=Node(node.next.val,[],[])
queue.append(node.next)
if node.random and node.random not in visited:
queue.append(node.random)
visited[node].next=visited.get(node.next)
visited[node].random=visited.get(node.random)
return node
return bfs(head)
方法三:迭代
這個方法比較直接,就是分別拷貝next結點和random結點。
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
#構建一個鏈表來記錄
visited={}
def getCloneNode(node):
if node:
if node not in visited:
visited[node]=Node(node.val,None,None)
return visited[node]
else:
return visited[node]
if not head:
return head
old_node=head
new_node=Node(old_node.val,None,None)
visited[old_node]=new_node
while old_node:
new_node.next=getCloneNode(old_node.next)
new_node.random=getCloneNode(old_node.random)
old_node=old_node.next
new_node=new_node.next
return visited[head]