吳恩達-deep learning 01.神經網路與深度學習Week2
Week2:神經網路的程式設計基礎(Basics of Neural Network programming)
Pre:本章基本字母含義

2.1 Binary Classification(二分法)
邏輯迴歸模型一般用來解決二分類(Binary Classification)問題。
- 二分類就是輸出y只有{0,1}兩個離散值(也有{-1,1}的情況)。
- 以一個影象識別問題爲例,判斷圖片中是否有貓存在,0代表no cat,1代表cat。

- 彩色圖片包含RGB三個通道。例如該cat圖片的尺寸爲(64,64,3)。在神經網路模型中,我們首先要將圖片輸入(維度是(64,64,3))轉化爲一維的特徵向量(feature vector)。方法是每個通道一行一行取,再連線起來。由於64x64x3=12288,則轉化後的輸入特徵向量維度爲(12288,1)。此特徵向量是列向量,維度一般記爲。
- 如果訓練樣本共有張圖片,那麼整個訓練樣本X組成了矩陣,維度是。注意,這裏矩陣的行代表了每個樣本特徵個數,列代表了樣本個數。
- Python實現的時候,你會看到
X.shape,這是一條Python命令,用於顯示矩陣的規模,即X.shape等於
2.2 Logistic Regression(邏輯迴歸)
2.3 Logistic Regression Cost Function(邏輯迴歸的損失函數)
參照吳恩達《機器學習》Week3的邏輯迴歸和代價/損失函數。
2.4 Gradient Descent(邏輯迴歸的梯度下降法)
- 問題提出
對單個數據邏輯迴歸的損失函數是:,個樣本的損失函數是:
所以在訓練邏輯迴歸模型時候,我們需要找到合適的和,來讓代價函數 的總代價降到最低。其中: - 梯度下降法
- 由於J(w,b)是convex function,梯度下降演算法是先隨機選擇一組參數w和b值,然後每次迭代的過程中分別沿着w和b的梯度(偏導數)的反方向前進一小步,不斷修正w和b。每次迭代更新w和b後,都能讓J(w,b)更接近全域性最小值。梯度下降的過程如下圖所示:
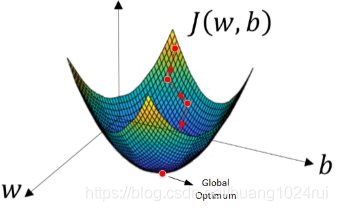
- 梯度下降演算法每次迭代更新,w和b的修正表達式爲:
- 上式中,是學習因子(learning rate),表示梯度下降的步進長度。
- 越大,和每次更新的「步伐」更大一些;
- 越小,和每次更新的「步伐」更小一些。
- 在程式程式碼中,我們通常使用來表示,用來表示。
微積分裡,表示對單一變數求導數,表示對多個變數中某個變數求偏導數。
- 由於J(w,b)是convex function,梯度下降演算法是先隨機選擇一組參數w和b值,然後每次迭代的過程中分別沿着w和b的梯度(偏導數)的反方向前進一小步,不斷修正w和b。每次迭代更新w和b後,都能讓J(w,b)更接近全域性最小值。梯度下降的過程如下圖所示:
2.5 Derivatives(求導)
2.6 More Derivative Examples
這兩節是求導和求導的例子。
2.7 Computation graph(計算圖)
整個神經網路的訓練過程實際上包含了兩個過程:正向傳播(Forward Propagation) 和 反向傳播(Back Propagation)。
- 正向傳播是從輸入到輸出,由神經網路計算得到預測輸出的過程;
- 反向傳播是從輸出到輸入,對參數w和b計算梯度的過程。
- 用計算圖(Computation graph)的形式來理解這兩個過程。舉個簡單的例子,假如Cost function爲,包含三個變數。我們用表示,表示,則。它的計算圖可以寫成如下圖所示:
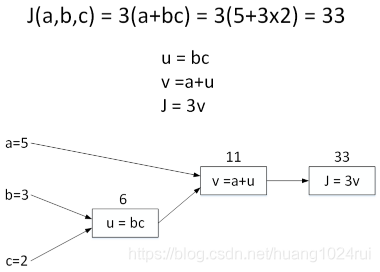
- 令,則 。計算圖中,這種從左到右,從輸入到輸出的過程就對應着神經網路或者邏輯迴歸中輸入與權重經過運算計算得到Cost function的。
2.8 Derivatives with a Computation Graph(計算圖的求導)
上一節介紹了計算圖的正向傳播(Forward Propagation),下面 下麪來介紹計算圖的反向傳播(Back Propagation),即計算輸出對輸入的偏導數。
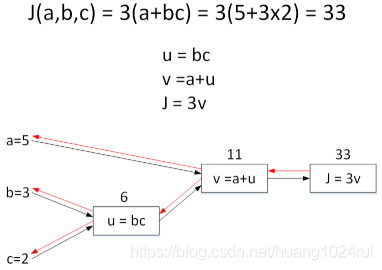
還是上個計算圖的例子,輸入參數有3個,分別是。
- 首先計算J對參數a的偏導數。從計算圖上來看,從右到左,是的函數,是的函數。則利用求導技巧,可以得到:
- 根據這種思想,然後計算對參數的偏導數。從計算圖上來看,從右到左,是的函數,是的函數,是的函數。可以推導:
- 最後計算對參數的偏導數。仍從計算圖上來看,從右到左,是的函數,是的函數,是的函數。可以推導:
2.9 Logistic Regression Gradient Descent(邏輯迴歸的梯度下降法)
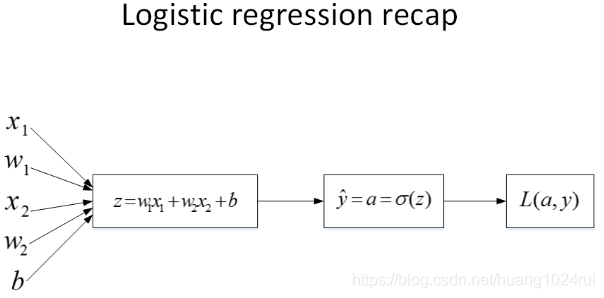
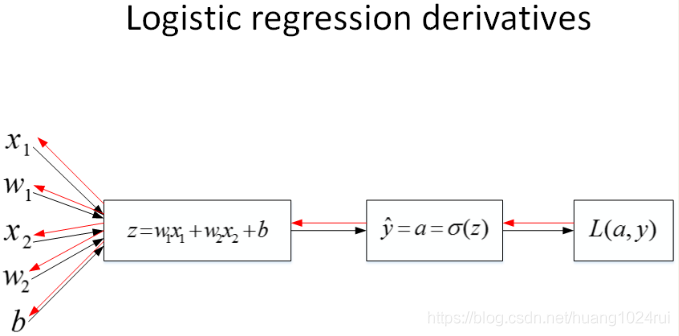
將對邏輯迴歸進行梯度計算。對單個樣本而言,邏輯迴歸Loss function表達式如下:
-
首先是正向傳播過程。根據上述公式,例如輸入樣本有兩個特徵,相應的權重維度也是,即。則,Loss function的計算圖如上圖。
-
然後,計算該邏輯迴歸的反向傳播過程,即由Loss function計算參數w和b的偏導數。推導過程如下:
知道了dz之後,就可以直接對w_1,w_2和b進行求導了。
則梯度下降演算法可表示爲:
2.10 Gradient descent on m examples(m個樣本的梯度下降法)
在之前的視訊中,你已經看到如何計算導數,以及應用梯度下降在邏輯迴歸的一個訓練樣本上。現在我們想要把它應用在個訓練樣本上。個樣本,其Cost function表達式如下:
- 和的偏導數可以寫成和平均的形式:
這樣,每次迭代中和的梯度有個訓練樣本計算平均值得到。其演算法流程圖如下所示:J=0; dw1=0; dw2=0; db=0; for i = 1 to m z(i) = wx(i)+b; a(i) = sigmoid(z(i)); J += -[y(i)log(a(i))+(1-y(i))log(1-a(i)); dz(i) = a(i)-y(i); dw1 += x1(i)dz(i); dw2 += x2(i)dz(i); db += dz(i); J /= m; dw1 /= m; dw2 /= m; db /= m; - 經過每次迭代後,根據梯度下降演算法,w和b都進行更新:
這樣經過次迭代後,整個梯度下降演算法就完成了。 - 這種計算中有兩個缺點,也就是說應用此方法在邏輯迴歸上你需要編寫兩個for回圈。
- 第一個for回圈是一個小回圈遍歷個訓練樣本,第二個for回圈是一個遍歷所有特徵的for回圈。
- 如果你有更多特徵,你開始編寫你的因此,,你有相似的計算從一直下去到。所以看來你需要一個for回圈遍歷所有個特徵。
- 深度學習演算法,在程式碼中顯式地使用for回圈使你的演算法很低效,同時在深度學習領域會有越來越大的數據集。需要使用矩陣,進行向量化處理。
2.11 向量化(Vectorization)
向量化是非常基礎的去除程式碼中for回圈的藝術,在深度學習安全領域、深度學習實踐中,你會經常發現自己訓練大數據集,因爲深度學習演算法處理大數據集效果很棒,所以你的程式碼執行速度非常重要。
- 以python爲例子,向量化來加速運算(np.function),遍歷遍的回圈可以寫成:
z=np.dot(w, x) + b
輸出結果類似於:import numpy as np #匯入numpy庫 a = np.array([1,2,3,4]) #建立一個數據a print(a) # [1 2 3 4] import time #匯入時間庫 a = np.random.rand(1000000) b = np.random.rand(1000000) #通過round隨機得到兩個一百萬維度的陣列 tic = time.time() #現在測量一下當前時間 #向量化的版本 c = np.dot(a,b) toc = time.time() print("Vectorized version:" + str(1000*(toc-tic)) +"ms") #列印一下向量化的版本的時間 #繼續增加非向量化的版本 c = 0 tic = time.time() for i in range(1000000): c += a[i]*b[i] toc = time.time() print(c) print("For loop:" + str(1000*(toc-tic)) + "ms")#列印for回圈的版本的時間250286.989866 Vectorized version:1.5027523040771484ms 250286.989866 For loop:474.29513931274414ms - 爲了加快深度學習神經網路運算速度,可以使用比CPU運算能力更強大的GPU。事實上,GPU和CPU都有並行指令(parallelization instructions),稱爲Single Instruction Multiple Data(SIMD)。SIMD是單指令多數據流,能夠複製多個運算元,並把它們打包在大型暫存器的一組指令集。SIMD能夠大大提高程式執行速度。
- python的numpy庫中的內建函數(built-in function)就是使用了SIMD指令。
- 相比而言,GPU的SIMD要比CPU更強大一些。
2.12 向量化的更多例子(More Examples of Vectorization)
- 在python的numpy庫中,我們通常使用np.dot()函數來進行矩陣運算。當你想寫回圈時候,檢查numpy是否存在類似的內建函數,從而避免使用回圈(loop)方式。
- numpy庫有很多向量函數。比如
u=np.log是計算對數函數()、np.abs()計算數據的絕對值、np.maximum(v, 0)按元素計算中每個元素和和0相比的最大值,v**2代表獲得元素 每個值的平方、1/v獲取 中每個元素的倒數等等。
2.13 向量化邏輯迴歸(Vectorizing Logistic Regression)
- 常規回圈
首先我們回顧一下邏輯迴歸的前向傳播步驟。如果有 個訓練樣本,然後對第一個樣本進行預測,你需要這樣計算。- 計算 ,我正在使用這個熟悉的公式 。然後計算啓用函數 ,計算第一個樣本的預測值 。
- 然後對第二個樣本進行預測,你需要計算 , 。
- 然後對第三個樣本進行預測,你需要計算 , ,依次類推。
- 如果你有 個訓練樣本,你可能需要這樣做 次。
- 向量表示
- 定義了一個矩陣 作爲訓練輸入,每個樣本是,將不同的列中堆積在一起。這是一個 行 列的矩陣。我現在將它寫爲Python numpy的形式 ,這只是表示 是一個 乘以 的矩陣 。
- , ……一直到 ,所有值都是在同一時間內完成。
是一個 的向量或者 的矩陣或者是一個 維的行向量。所以希望你熟悉矩陣乘法,你會發現的 轉置乘以 , 一直到 。繼續簡化可以寫成:
其中大寫的 表示爲 , 這是第一個元素, 這是第二個元素, 這是第 個元素。
- Python表示
- numpy命令是
Z=np.dot(w.T,X)+b;最後再進行函數,一次性表示出。 - 這裏在Python中有一個巧妙的地方,這裏 是一個實數,或者你可以說是一個 矩陣。但是當你將這個向量加上這個實數時,Python自動把這個實數 擴充套件成一個 的行向量。在Python中被稱作廣播(brosdcasting),後邊會具體介紹。
- numpy命令是
2.14 向量化 logistic 迴歸的梯度輸出(Vectorizing Logistic Regression’s Gradient)
注:本節中大寫字母代表向量,小寫字母代表元素
- 在本節中,已經給出了邏輯迴歸中梯度下降法的一般表示形式:
- 接下來看看邏輯迴歸中的梯度下降演算法如何轉化爲向量化的矩陣形式,對於所有個樣本。
- 的維度是,可表示爲:
- 可表示爲:
對應的程式爲:db = 1/m*np.sum(dZ) - 可表示爲:
對應的程式爲:dw = 1/m*np.dot(X,dZ.T) - 我們把整個邏輯迴歸中的回圈儘可能用矩陣運算代替,對於單次迭代,梯度下降演算法流程如下所示:
其中是學習因子,決定和的更新速度。上述程式碼只是對單次訓練更新而言的,外層還需要一個回圈,表示迭代次數。Z = np.dot(w.T,X) + b A = sigmoid(Z) dZ = A-Y dw = 1/m*np.dot(X,dZ.T) db = 1/m*np.sum(dZ) w = w - alpha*dw b = b - alpha*db
- 的維度是,可表示爲:
2.15 Python 中的廣播(Broadcasting in Python)
- numpy廣播機制 機製
- 定義:對於四則運算及其混合形式,如果兩個陣列的後緣維度的軸長度相符或其中一方的軸長度爲1,則認爲它們是廣播相容的。廣播會在缺失維度和軸長度爲1的維度上進行。 python中的廣播機制 機製可由下面 下麪四條表示:
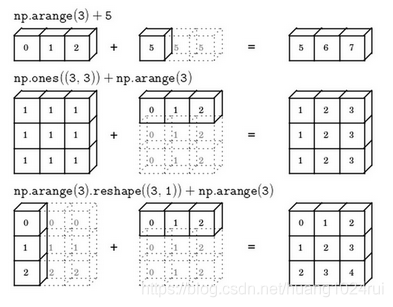
- 對於Matlab/Octave 有類似功能的函數
bsxfun。
- 定義:對於四則運算及其混合形式,如果兩個陣列的後緣維度的軸長度相符或其中一方的軸長度爲1,則認爲它們是廣播相容的。廣播會在缺失維度和軸長度爲1的維度上進行。 python中的廣播機制 機製可由下面 下麪四條表示:
- numpy中的axis
import numpy as np #輸入數據 A = np.array([[56.0, 0.0, 4.4, 68.0], [1.2, 104.0, 52.0, 8.0], [1.8, 135.0, 99.0, 0.9]]) print(A) # 求每列的和 cal = A.sum(axis= 0) print(cal)A.sum(axis = 0)中的參數axis。axis用來指明將要進行的運算是沿着哪個軸執行,在numpy中,0軸是垂直的,也就是列,而1軸是水平的,也就是行。
2.16 關於 python _ numpy 向量的說明(A note on python or numpy vectors)
本講Python中的numpy一維陣列的特性,以及與行向量或列向量的區別。並介紹在實際應用中的一些小技巧,去避免在coding中由於這些特性而導致的bug。
- 秩1:
這條語句生成的a的維度是(5,)。它既不是行向量也不是列向量,我們把a叫做rank 1 array(秩1)。這種定義會帶來一些問題。例如我們對a進行轉置,還是會得到a本身。a = np.random.randn(5) - 定義向量:
- 如果我們要定義(5,1)的列向量或者(1,5)的行向量,最好使用下來標準語句,避免使用rank 1 array。
a = np.random.randn(5,1) b = np.random.randn(1,5) - 可以使用
assert語句對向量或陣列的維度進行判斷,例如:
assert會對內嵌語句進行判斷,即判斷a的維度是不是(5,1)的。如果不是,則程式在此處停止。使用assert語句也是一種很好的習慣,能夠幫助我們及時檢查、發現語句是否正確。assert(a.shape == (5,1)) - 還可以使用
reshape函數對陣列設定所需的維度:a.reshape((5,1))
- 如果我們要定義(5,1)的列向量或者(1,5)的行向量,最好使用下來標準語句,避免使用rank 1 array。
2.17 Jupyter/iPython Notebooks快速入門(Quick tour of Jupyter/iPython Notebooks)
Python安裝Jupyter Notebook設定使用教學
2.18 (選修)logistic 損失函數的解釋(Explanation of logistic regression cost function)
我們介紹過邏輯迴歸的Cost function。接下來我們將簡要解釋這個Cost function是怎麼來的。
-
預測輸出的表達式可以寫成:
其中,。可以看成是預測輸出爲正類的概率:- 當時:
- 當時:
-
把上面兩個式子整合到一個式子中,得到:
由於函數的單調性,可以對上式進行log處理:
上述概率越大越好,對上式加上負號,則轉化成了單個樣本的Loss function,越小越好,也就得到了我們之前介紹的邏輯迴歸的Loss function形式。
-
如果對於所有m個訓練樣本,假設樣本之間是獨立同分佈的(iid),我們希望總的概率越大越好:
引入函數,加上負號,將上式轉化爲Cost function:
上式中,表示對所有個樣本的Cost function求平均,是縮放因子。
本章總結
本節主要介紹了神經網路基礎——python和向量化。使用向量化和矩陣運算的方法能夠大大提高執行速度,節省時間。以邏輯迴歸爲例,我們將其演算法流程包括梯度下降轉換爲向量化的形式。
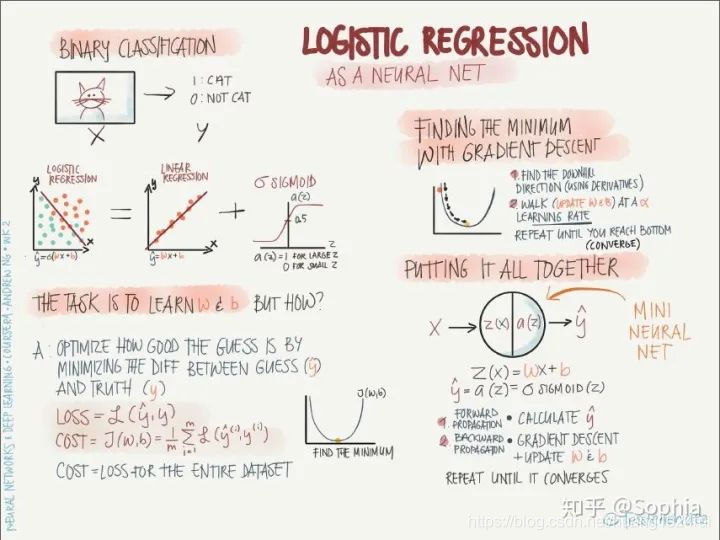
-
左上:
logistic 迴歸主要用於二分類問題,如圖中所示,logistic 迴歸可以求解一張影象是不是貓的問題,其中影象是輸入(x),貓(1)或非貓(0)是輸出。我們可以將 logistic 迴歸看成將兩組數據點分離的問題,如果僅有線性迴歸(啓用函數爲線性),則對於非線性邊界的數據點(例如,一組數據點被另一組包圍)是無法有效分離的,因此在這裏需要用非線性啓用函數替換線性啓用函數。在這個案例中,我們使用的是 sigmoid 啓用函數,它是值域爲(0, 1)的平滑函數,可以使神經網路的輸出得到連續、歸一(概率值)的結果。 -
左下: 神經網路的訓練目標是確定最合適的權重 和偏置項 ,那這個過程是怎麼樣的呢?
這個分類其實就是一個優化問題,優化過程的目的是使預測值 和真實值 之間的差距最小,形式上可以通過尋找目標函數的最小值來實現。所以我們首先確定目標函數(損失函數、代價函數)的形式,然後用梯度下降逐步更新 、,當損失函數達到最小值或者足夠小時,我們就能獲得很好的預測結果。 -
右上:
損失函數值在參數曲面上變化的簡圖,使用梯度可以找到最快的下降路徑,學習率的大小可以決定收斂的速度和最終結果。學習率較大時,初期收斂很快,不易停留在區域性極小值,但後期難以收斂到穩定的值;學習率較小時,情況剛好相反。一般而言,我們希望訓練初期學習率較大,後期學習率較小,之後會介紹變化學習率的訓練方法。 -
右下: 總結整個訓練過程,從輸入節點 開始,通過前向傳播得到預測輸出 ,用 和得到損失函數值,開始執行反向傳播,更新和,重複迭代該過程,直到收斂。