Feature Pyramid Transformer論文閱讀翻譯

論文下載地址：點選此鏈接跳轉.
這是博主自己在github整理的目標檢測方向論文的合集，應該算比較全，目前2020ECCV持續更新中，即將更新：2020IJCAI合集，歡迎下載…

一、Abstract

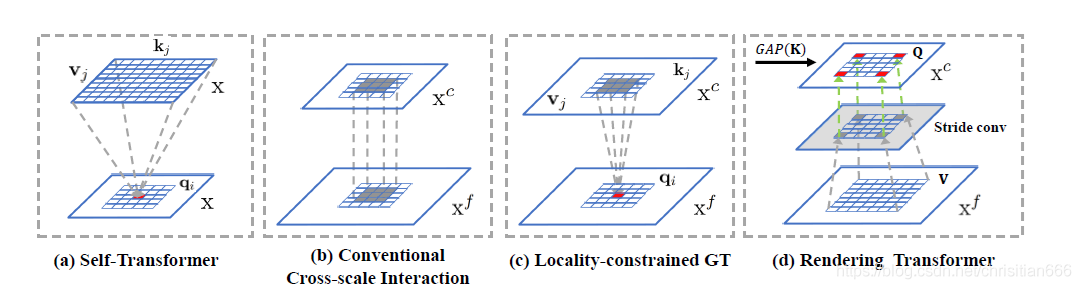
       跨空間和尺度的特徵融合是當代視覺識別系統的基礎，因爲引入了有用的視覺上下文資訊。以往空間上下文都是被動地隱藏在CNN不斷變大的感知野中，或者是主動通過non-local進行編碼。但是non-local的空間互動並不是跨尺度的，它們無法捕獲不同尺度中的目標的non-local上下文。爲此，作者提出了一種跨空間及尺度的完全啓用的特徵融合，稱爲Feature Pyramid Transformer（FPT）。通過使用了三個自上而下或自下而上transformer將特徵金字塔轉換具有更豐富上下文資訊的特徵金字塔。 FPT可作爲通用的視覺backbone，計算開銷大小也較爲合理。作者在範例級（目標檢測和範例分割）和畫素級分割任務中進行了廣泛的實驗，存在一致的改進。

二、Introduction

       現代視覺識別系統與語意資訊息息相關，由於CNN的結構，經過池化，空洞折積等，上下文資訊會在逐漸變大的接收域中被編碼。因此，最後一層的特徵圖會有豐富的上下文資訊，對於那些一個特徵畫素的較小物件，由於上下文資訊較充足，也可以被識別到。
       當然尺度也很重要，對較小目標的識別應該分配更多的特徵畫素，而不僅僅只是在最後的特徵圖上的畫素，這樣會很容易忽略小目標。傳統的解決方案是對同一影象構建一個影象金字塔，較高/低層級對應着較低/高的解析度，例如較低層級的滑鼠解析度會較高，而較高層級的桌子解析度會較低。但是由於每張影象都需經CNN後再進行識別，使用影象金字塔會使CNN前向傳播的時間倍增。而CNN中存在着一個內部的特徵金字塔，較低/較高層級的特徵圖表示較高/較低解析度的視覺內容，並且不需要額外的計算開銷。如下圖(b)所示，這樣我們就可以使用不同層級的特徵圖來識別不同大小的物體。
       有時我們會需要組合多個尺度的上下文資訊，尤其是對於畫素級標記的識別(語意分割)。下圖©中，對於部分割區域中的畫素，低層級的區域性上下文資訊可能就足夠了。但是對於螢幕區域中的畫素，我們需要從更高層級上同時利用區域性上下文和全域性上下文，因爲顯示器螢幕的外觀會接近於TV螢幕，所以我們應該使用鍵盤和滑鼠等場景上下文來區分兩種型別。
       通過使用non-local折積和自注意力，我們可以顯式地和主動地對non-local上下文資訊進行建模。預期這種空間特徵互動可以捕捉到多個目標同時出現的情形，如下圖(d)所示，電腦更可能是在桌子上而不是在路上，因此，識別其中一個對另一個是有幫助的。
       上下文資訊和尺度間的聯繫應該延續下去，這是作者的motivation，尤其是受到了跨尺度融閤中忽略的non-local的空間相互作用的啓發。作者相信non-local互動本身應當在互動目標對應的尺度上進行，而不是像現有方法那樣僅在一個統一的尺度上進行。下圖(e)表示了跨尺度的non-local互動，低層次的滑鼠與高層次的計算機相互動，而計算機與桌面以相同尺度進行互動。

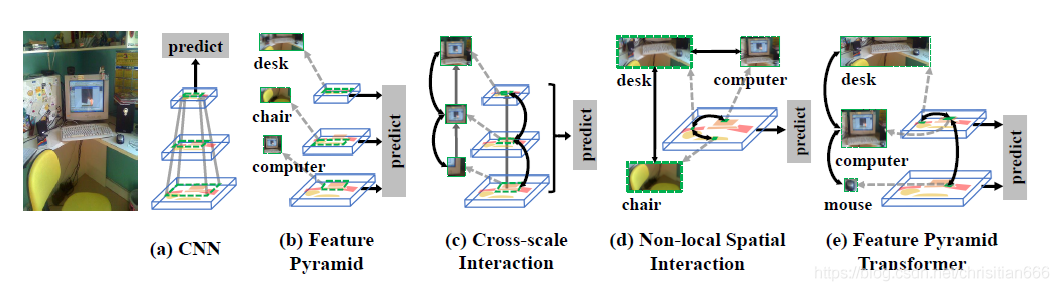
       對此，作者提出了一種新穎的特徵金字塔網路叫做Feature Pyramid Transformer (FPT)用於視覺識別，例如範例級和畫素級的任務。簡而言之，如圖所示，FPT的輸入是一個特徵金字塔，輸出是一個變換後的特徵金字塔，每一層級經跨空間和尺度的non-local互動後會更加豐富。顧名思義，FPT的融合採用的transformer形式，它具有更平滑整潔的query，key和value操作，在選擇資訊進行長程互動時非常有效，這也調整了我們的目標，在適當的尺度上進行non-local互動。另外還可以像其他transfomer模型一樣使用TPU來減輕計算開銷。

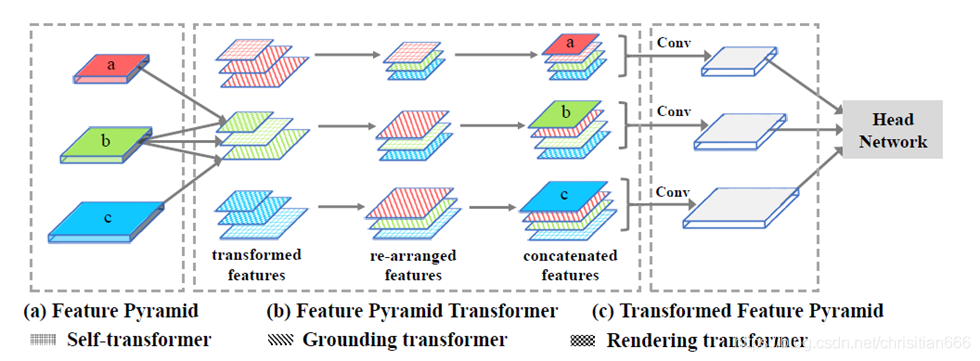
       如上圖所示，作者的contributions是設計了三個transformer，1）self-transformer(ST)，這是基於經典的同層特徵圖的non-local互動，輸出與輸入具有相同尺度。2）Groundng Transformer(GT)，採用自上而下的方式，輸出與低層級特徵圖尺度相同，作者將高層級特徵圖的concept植於低層級畫素中。由於不是必需使用全域性資訊來分割目標，並且local區域的上下文資訊更加豐富，出於對語意分割的效率和精確性間的權衡，作者還設計了一個locality-constrained GT。3）Rendering Transformer (RT) ，採用自下而上的方式，輸出的尺度與高層級特徵圖尺度相同。直觀地，我們是使用低層級畫素的視覺屬性來渲染高層級的concept。這是一種區域性互動，因爲用另一個太遠的目標的畫素來對當前畫素進行渲染是沒有意義的。然後再將每個層級變換後的特徵圖重新排列爲其對應原特徵圖的大小，與原特徵圖concat後輸入到折積中降至原本的通道數。大量實驗表明在MS-COCO test-dev上，FPT可以大大提高檢測/分割精度。

三、Feature Pyramid Transformer

       輸入一副影象，經cnn網路我們可以構建一個特徵金字塔，細粒度/粗粒度特徵圖分別處於低/高層級。作者將低層級的細粒度特徵圖表示爲X^f，高層級的粗粒度特徵圖表示爲X^c。FPT使特徵能夠跨越空間和尺度進行互動，分爲ST,GT,RT。

3.1 Non-Local Interaction Revisited

       non-local是對單個特徵圖X的queries(Q)、keys(K)和values(V)進行操作，輸出尺度相同的轉換後的X’。

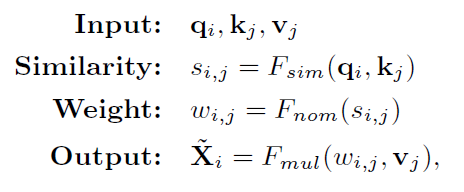
       q_i=f_q(X_i)∈Q是第i個query，k_j=f_k(X_j)∈K，v_j=f_v(X_j)∈V是第j個key/value，f_q(^.), f_k(^.), f_v(^.)是q, k, v的轉換函數。X_i和X_j是X中第i個和第j個位置。F_sim是相似度函數(點積或高斯嵌入)，F_nom是歸一化函數(預設爲softmax)，F_mul是權重聚合函數(預設爲矩陣相乘)，X’_i是轉換後的特徵圖X’的第i個位置。

3.2 Self-Transformer

       Self-Transformer的目的是捕獲在一個特徵圖上共現的目標特徵。ST是一種改進的non-local，輸出特徵圖X’與輸入X的尺度相同。和原本不同的是，作者部署了一個混合softmaxes(MoS)作爲歸一化函數F_mos，這比標準的Softmax在影象上更有效。並且作者將q_i和k_j分爲N塊，然後是去計算的每一塊的相似度分數sⁿ_i,j，基於MoS的歸一化函數Fmos如下所示：

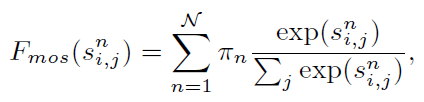
       Sⁿ_i,j是第n塊的相似度分數。π_n是第n個聚合權重，等於Softmax(w^T_nk)，w_n是一個可學習的用於歸一化的線性向量，k是所有kj的算術平均數。基於F_mos，我們可以重新表示Eq1：

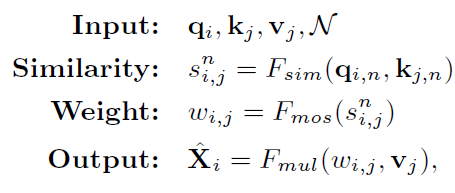
3.3 Grounding Transformer

       GT是一種自上而下的non-local互動，將高層特徵圖Xc中的概念融進低層級Xf的畫素中。輸出X’^f和Xf的尺度相同。通常不同尺度的影象特徵會提取出不同的語意或上下文資訊，或者兩者都是。並且當兩個特徵圖的語意資訊不同時，歐氏距離的負值F_eud在計算相似度時會比點積更有效。所以我們更傾向於使用F_eud作爲相似度函數，表示爲:

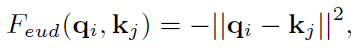
       q_i=f_q(X^f_i)，k_j=f_k(X^c_j)，X^f_i是X^f中的第i個特徵位置，X^c_j是X^c中的第j個位置，作者即將相似度函數替換爲F_eud，式子又變爲：

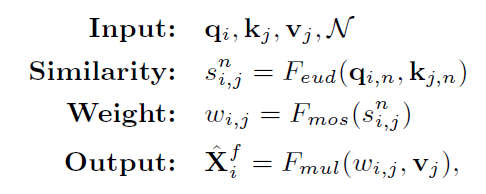
       v_j=f_v(X^c_j)，X’^f_i是X’_f的第i個轉換後的特徵位置。根據上式，每一對q_i和k_j距離越近，其權重越大，與點積的結果相比，使用F_eud在自上而下的互動中帶來了明顯的改進。
在特徵金字塔中，高/低層級的特徵圖包含了大量的全域性/區域性影象資訊。而對跨尺度特徵互動的語意分割，是無需使用全域性資訊對影象中的兩個目標進行分割的。query位置附近的區域性區域內的上下文會包含更多的資訊。如上圖b所示，它們本質上是隱式的local style。而作者預設的GT是global互動。

Locality-constrained Grounding Transformer.

       因此，作者引入了一個GT的區域約束版本，稱爲區域約束GT (LGT) 用於語意分割，這是一個顯式的區域性特徵互動。如圖3©所示，每個qi(即底層特徵圖上的紅色網格)與一部分在中心座標與qi相同、邊長爲正方形的區域性正方形區域內的kj和vj互動(高層級特徵圖上的藍色網格)。對於超出索引的k_j和v_j位置，我們記爲0值。

3.4 Rendering Transformer

       RT以自下而上的方式工作，通過合併低層級中的視覺屬性來呈現高層級的概念，如上圖d所示，RT是一種區域性互動，有考慮到用來自另一個遙遠物件的特性或屬性來呈現一個物件是沒有意義的。
       在作者的實現中，RT不是按畫素進行的，而是對於整個特徵圖。作者將高層級的特徵圖定義爲Q；將低層級特徵圖定義爲K和V。爲了突出顯示渲染目標，Q和K之間的互動逐通道進行。 K首先通過全域性平均池化（GAP）計算Q的權重w。然後，加權後的Q（即Qatt）經3×3折積進行細化，V經一個3×3折積減小特徵圖大小（上圖（d）中的灰色正方形）。最後將精細化的Qatt和下採樣的V（即V_dow）求和，並通過另一個3×3折積進行處理以進行渲染。提出的RT可以如下表示：

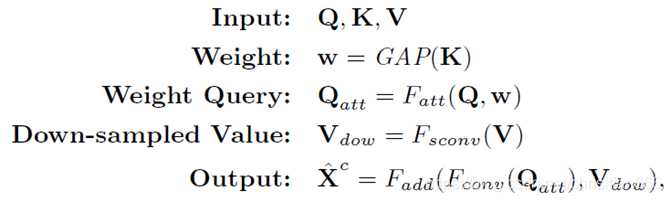
       F_att(^.)是一個外積函數，F_sconv(^.)是一個3 * 3的步長折積，當Q和V的尺度相等時步長爲1，Fconv(^.)時候是一個用於精細化的3 * 3折積，Fadd(^.)是帶着一個3 * 3折積的求和函數，X’^c表示RT的輸出特徵圖。

3.5 Overall Architecture

       作者構建了一個FPT網路來處理目標檢測，範例分割和語意分割，FPT網路由四部分組成，提取特徵的backbone，一個特徵金字塔構建模組，FPT，和用於特定任務的head。經過FPT後得到的轉換後的特徵圖與原特徵圖concat，然後經一個3*3折積將通道降維至256。

四、個人總結

       這篇工作的中心思想就是認爲僅在一個尺度的特徵圖上進行non-local互動不足以表達上下文，想要在相互作用的目標(或部分)的相應尺度上做non-local。對於每一層的特徵圖，會輸入與其鄰近的兩層特徵圖，也就是FPT中每層都會輸入三個尺度的特徵，然後分別從ST，GT，RT中選其中一種來做這個變換後的non-local，以中間那層尺度爲例，輸入a, b, c三個尺度的特徵，a和b做的是RT，b做ST，b和c做GT。然後將經過non-local的特徵圖變爲和b相同的尺度，然後與原圖做一個concat，最後經一個折積降維至原本的維度。ST就是將原本的non-local中的softmax換成了MoS，然後還將q_i和k_j分爲N塊，然後去計算的每一塊的相似度分數。GT是在ST的基礎上，將原本用的點積，Embeded gaussian換成了歐氏距離的負值，本來想試試效果，但作者當前的程式碼還沒把這個放出來，不知道效果是不是如作者所說會相對較好，也沒有消融實驗。RT則不再是按畫素來進行的non-local計算，而是對於的整個特徵圖。