物以類聚，聚類演演算法使用最佳化的演演算法來計算資料點之間的距離，並將它們分組到最近的簇中。

Scipy的聚類模組中，進一步分為兩個聚類子模組：

vq（vector quantization）：提供了一種基於向量量化的聚類演演算法。

vq模組支援多種向量量化演演算法，包括K-means、GMM（高斯混合模型）和WAVG（均勻分佈）。

hierarchy：提供了一種基於層次聚類的聚類演演算法。

hierarchy模組支援多種層次聚類演演算法，包括ward、elbow和centroid。

總之，Scipy中的vq和hierarchy模組都提供了一種基於最小化平方誤差的聚類演演算法，
它們可以幫助我們快速地對大型資料集進行分組，從而更好地理解資料的分佈和模式。

1. vq 聚類

vq 聚類演演算法的原理是將資料點對映到一組稱為「超空間」的低維向量空間中，然後將它們分組到最近的簇中。

首先，我們建立一些測試資料：（建立3個類別的測試資料）

import numpy as np
import matplotlib.pyplot as plt

data1 = np.random.randint(0, 30, (100, 3))
data2 = np.random.randint(30, 60, (100, 3))
data3 = np.random.randint(60, 100, (100, 3))

data = np.concatenate([data1, data2, data3])

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.scatter(data[:, 0], data[:, 1], data[:, 2])
plt.show()

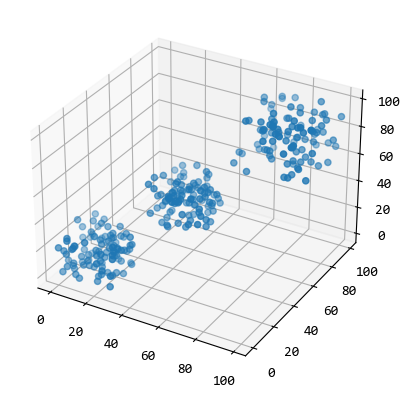
data1，data2，data3分佈在3個區域，
每個資料集有100條資料，每條資料有3個屬性。

1.1. 白化資料

聚類之前，一般會對資料進行白化，所謂白化資料，是指將資料集中的每個特徵或每個樣本的值都統一為同一個範圍。
這樣做的目的是為了消除特徵之間的量綱和數值大小差異，使得不同特徵具有相似的重要性，從而更容易進行聚類演演算法。

在聚類之前對資料進行白化處理也被稱為預處理階段。

from scipy.cluster.vq import whiten

# 白化資料
normal_data = whiten(data)

# 繪製白化後的資料
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.scatter(normal_data[:, 0], normal_data[:, 1], normal_data[:, 2])
plt.show()

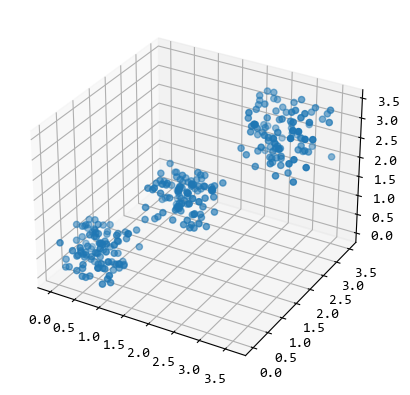
從圖中可以看出，資料的分佈情況沒有改變，只是資料的範圍從0~100變成0.0~3.5。
這就是白化的效果。

1.2. K-means

白化之後，就可以用K-meas方法來進行聚類運算了。
scipy的vq模組中有2個聚類函數：kmeans和kmeans2。

kmeans函數最少只要傳入兩個引數即可：

需要聚類的資料，也就是上一步白化的資料
聚類的數目

返回值有2部分：

各個聚類的中心點
各個點距離聚類中心點的歐式距離的平均值

from scipy.cluster.vq import kmeans 

center_points, distortion = kmeans(normal_data, 3)
print(center_points)
print(distortion)
# 執行結果
[[1.632802   1.56429847 1.51635413]
 [0.48357948 0.55988559 0.48842058]
 [2.81305235 2.84443275 2.78072325]]
0.5675874109728244

把三個聚類點繪製在圖中來看更加清楚：

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.scatter(normal_data[:, 0], 
           normal_data[:, 1], 
           normal_data[:, 2])
ax.scatter(
    center_points[:, 0],
    center_points[:, 1],
    center_points[:, 2],
    color="r",
    marker="^",
    linewidths=5,
)

plt.show()

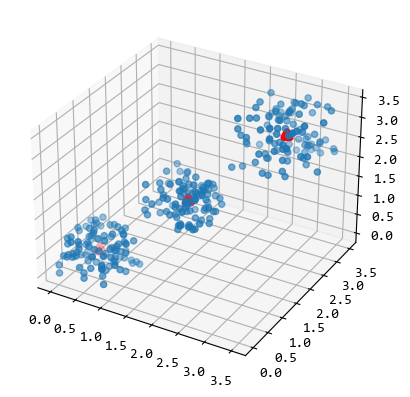
圖中3個紅色的點就是聚類的中心點。

1.3. K-means2

kmeans2函數使用起來和kmeans類似，但是返回值有區別，
kmeans2的返回的是：

聚類的中心點座標
每個聚類中所有點的索引

from scipy.cluster.vq import kmeans2

center_points, labels = kmeans2(normal_data, 3)
print(center_points)
print(labels)
# 執行結果
[[2.81305235 2.84443275 2.78072325]
 [1.632802   1.56429847 1.51635413]
 [0.48357948 0.55988559 0.48842058]]
[2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 ... ...
 0 0 0 0]

可以看出，計算出的聚類中心點center_points和kmeans一樣（只是順序不一樣），
labels有0,1,2三種值，代表normal_data中每個點屬於哪個分類。

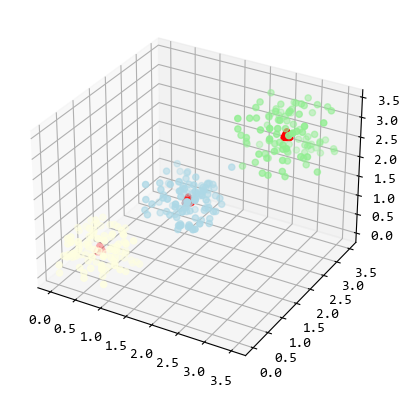
kmeans2除了返回了聚類中心點，還有每個資料點屬於哪個聚類的資訊，
所以我們繪圖時，可以將屬於不同聚類的點標記不同的顏色。

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
arr_data = [[], [], []]
for idx, nd in enumerate(normal_data):
    arr_data[labels[idx]].append(nd)

data = np.array(arr_data[0])
ax.scatter(data[:, 0], data[:, 1], data[:, 2], color='lightblue')
data = np.array(arr_data[1])
ax.scatter(data[:, 0], data[:, 1], data[:, 2], color='lightgreen')
data = np.array(arr_data[2])
ax.scatter(data[:, 0], data[:, 1], data[:, 2], color='lightyellow')

ax.scatter(
    center_points[:, 0],
    center_points[:, 1],
    center_points[:, 2],
    color="r",
    marker="^",
    linewidths=5,
)

plt.show()

2. hierarchy 聚類

hierarchy聚類演演算法的步驟比較簡單：

將每個樣本視為一個簇
計算各個簇之間的距離，將距離最近的兩個簇合併為一個簇
重複第二個步驟，直至到最後一個簇

from scipy.cluster.hierarchy import ward, fcluster, dendrogram
from scipy.spatial.distance import pdist

# 計算樣本資料之間的距離
# normal_data是之前白化之後的資料
dist = pdist(normal_data)

# 在距離上建立Ward連線矩陣
Z = ward(dist)

# 層次聚類之後的平面聚類
S = fcluster(Z, t=0.9, criterion='distance')
print(S)
# 執行結果
[20 26 23 18 18 22 18 28 21 22 28 26 27 27 20 17 23 20 26 23 17 25 20 22
 ... ...
  5 13  3  4  2  9  9 13 13  8 11  6]

返回的S中有300個資料，和normal_data中的資料一樣多，S中數值接近的點，分類越接近。

從數值看聚類結果不那麼明顯，scipy的層次聚類提供了一個dendrogram方法，內建了matpltlib的功能，
可以把層次聚類的結果用圖形展示出來。

P = dendrogram(Z, no_labels=True)
plt.show()

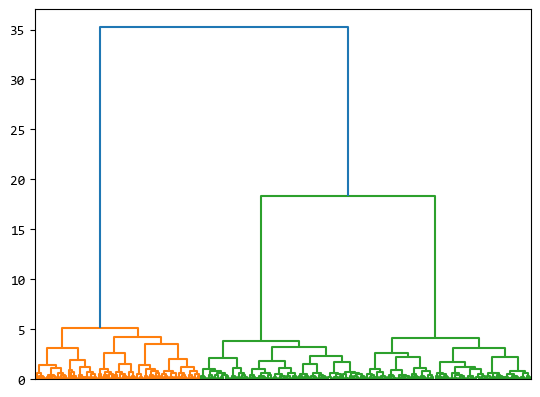
從這個圖可以看出每個資料分別屬於哪個層次的聚類。
最底層的葉子節點就是normal_datad中的各個資料，這些資料的索引資訊可以從 P 中獲取。

# P是一個字典，包含聚類之後的資訊
# key=ivl 是圖中最底層葉子節點在 normal_data 中的索引
print(P["ivl"])
# 執行結果
['236', '269', '244', ... ... '181', '175', '156', '157']

3. 總結