引言

在之前的章節中，我們已經詳細介紹了計算機硬體的組成部分，包括中央處理器（CPU）、記憶體、磁碟和匯流排等。因此，從今天開始，我們將深入探討計算機內部的工作原理。首先，我們將從二進位制這個簡單而重要的概念開始講解，因為計算機底層只能使用二進位制來表示和處理資訊。

二進位制

我們都知道，計算機的底層使用二進位制資料進行資料流傳輸。那麼，為什麼計算機要使用二進位制表示呢？又什麼是二進位制數呢？更進一步地，我們如何使用二進位制進行加減乘除運算呢？接下來，我們將一一解答這些問題。

什麼是二進位制數

那麼，什麼是二進位制數呢？為了詳細說明這個問題，我們先將一個二進位制數 00100111 轉換為十進位制數進行觀察。將二進位制數轉換為十進位制數的方法是，直接將各個位置上的值乘以相應的位權，然後相加得到結果。那麼，讓我們來將上述的二進位制數轉換為十進位制數。

根據轉換規則，將二進位制數 00100111 轉換為十進位制數，結果為 39。這裡的 39 不是由數位 3 和 9 連在一起寫成的，而是由 3 乘以位權 10 和 9 乘以位權 1 相加得到的。而這些位權，從高位到低位依次為 7、6、5、4、3、2、1、0。這些位權也可以被稱為次冪，例如最高位的位權就是 2 的 7 次冪，第二位的位權就是 2 的 6 次冪，以此類推。

在二進位制數的運算中，每次運算都是以基數 2 作為底數。而十進位制數的基數則是 10。在任何情況下，位權的值都是數的位數減去 1。因此，第一位的位權為 1 - 1 = 0，第二位的位權為 2 - 1 = 1，以此類推。

移位運算和乘除的關係

在我們瞭解了二進位制數之後，接下來讓我們來探討一下二進位制數的運算。和十進位制數一樣，二進位制數也可以進行加減乘除運算，只需要注意到逢二進位即可。二進位制數的運算是計算機程式中的基礎運算，因此瞭解二進位制的運算是至關重要的。

首先，讓我們來介紹一下移位運算。移位運算是指將二進位制數的各個位置上的元素進行左移和右移操作。具體的操作可以參考下圖：

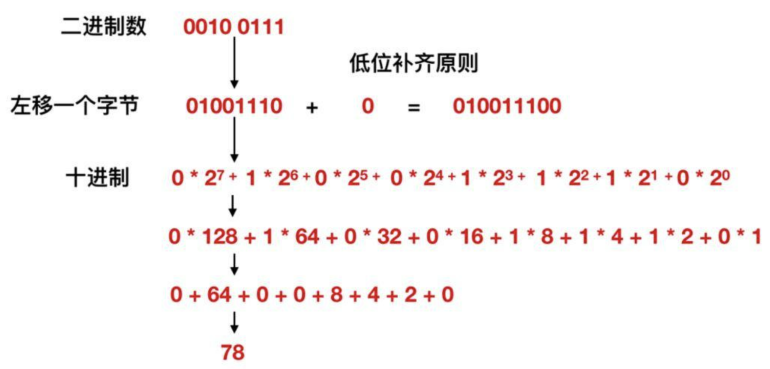
移位運算在計算機中被廣泛應用，可以用於快速進行乘以或除以2的冪次的運算。同時，移位運算也可以用來提取或插入二進位制數中的特定位。

除了移位運算，還有其他的二進位制運算，如按位元與、按位元或、按位元互斥或等。這些運算可以用於處理和操作二進位制資料，在電腦科學中有著重要的應用。

補數

剛才我們沒有介紹右移的情況，是因為右移之後空出來的高位數值有兩種形式：0和1。為了區分補0和補1的情況，我們需要了解二進位制數表示負數的方法。

一般來說，二進位制數中用最高位作為符號位來表示負數。符號位為0表示正數，為1表示負數。那麼如何用二進位制數表示-1呢？很多人可能會認為，因為1的二進位制是0000 0001，最高位是符號位，所以-1應該表示為1000 0001。但是這個答案是否正確呢？

實際上，計算機中沒有減法運算，計算機在做減法時實際上是通過加法來實現的，即用加法來表示減法運算。例如100-60，在計算機中實際上看作是100+(-60)。為了表示負數，我們需要使用二進位制二補數，即用正數表示負數。

為了得到二補數，我們需要將二進位制的各位數值全部取反，然後再加1。記住這個結論因為他適用於所有負數，下面我們來演示一下。

具體來說，要獲取某個數值的二進位制二補數，需要先獲取該數值的二進位制表示，然後對每一位進行取反操作（0變為1，1變為0），最後再將取反後的數值加1，這樣就得到了二補數。

儘管二補數的獲取可能在直觀上不容易理解，但在邏輯上是非常嚴謹的。舉個例子，我們來看一下1-1的過程。我們先用上面提到的1000 0001（我們假設它是1的二補數，如果不瞭解，請參考前文，先不管二補數是否是對的）來表示一下。

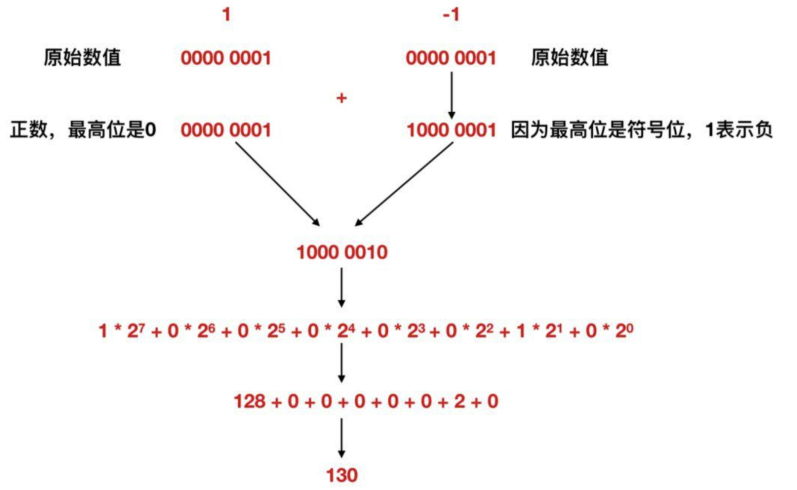
奇怪，1 - 1 為什麼會變成 130 而不是 0？這個結果看起來很奇怪，我們來分析一下。

對於正數 1，它的二進位制表示是 0000 0001。現在我們將其轉成二補數。首先取反各位得到 1111 1110，然後加1，得到二補數 1111 1111，即 -1 的二補數表示。

接下來，我們來驗證一下 -1 的二補數表示是否正確。

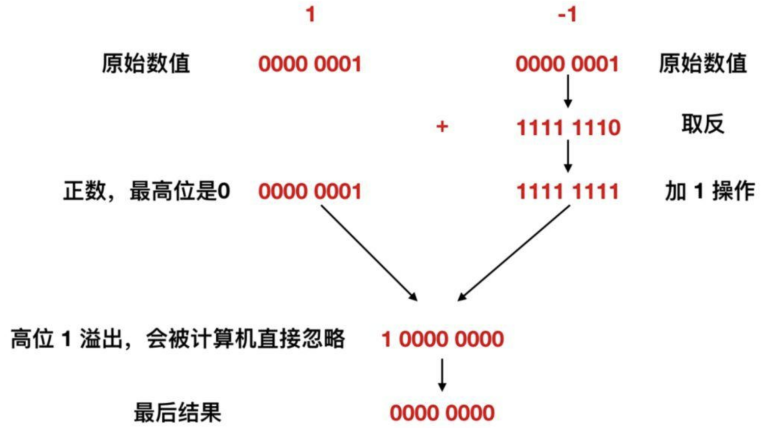
我們可以觀察到，1 - 1 實際上是 1 + (-1) 的運算。對於 -1，我們可以使用上面提到的方法來求其二補數表示。通過取反 + 1 的過程，我們得到了二補數 1111 1111。然後，將二補數 1111 1111 與 1 進行加法運算。

在加法運算中，我們會得到一個九位的結果 1 0000 0000。然而，在計算機中，發生了溢位的情況下，會直接忽略掉溢位位，即最高位的 1。因此，結果變為 0000 0000，即 0。所以，我們得出的結果是正確的，1111 1111 表示的是 -1。

綜上所述，負數的二進位制表示是通過先求其補數，即對原始數值的二進位制數各位取反，然後將結果加1。這樣可以得到正確的負數的二進位制表示。

算數右移和邏輯右移的區別

在瞭解了補數的概念之後，我們需要重新考慮一下右移這個問題。右移操作會導致最高位出現兩種情況，即0和1。

當我們將二進位制數作為帶符號的數值進行右移運算時，移位後需要在最高位填充移位前的符號位的值（0或1）。這種右移方式被稱為算術右移。如果數值是負數且使用二補數表示，那麼右移後需要在最高位補1，這樣才能正確地表示數值的1/2、1/4、1/8等運算結果。而如果是正數，則直接在最高位補0即可。

下面我們來看一個右移的例子，將-4右移兩位，大家可以參考移位示意圖來理解。

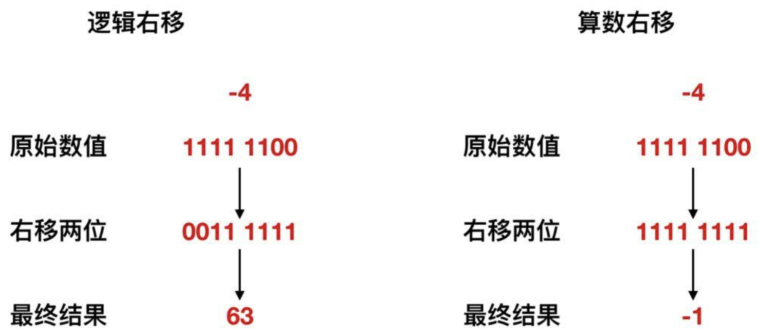
根據上圖所示，當進行邏輯右移操作時，-4右移兩位會變成63，顯然這不是它的1/4，因此邏輯右移不適用於這種情況。而在算數右移的情況下，-4右移兩位會變為-1，顯然這是它的1/4，所以我們選擇採用算數右移。

因此，我們可以得出一個結論：在左移操作中，無論是正數還是負數，只需要將低位補0即可；而在右移操作中，需要根據具體情況判斷是應該進行邏輯右移還是算數右移。

現在我要介紹一下符號擴充套件的概念。符號擴充套件是為了在保持數值不變的前提下，增加資料的位數，以滿足某些指令對運算元位數的要求。它可以用於使被除數比除數位數更長，或者用於增加資料位數以減少計算過程中的誤差。

以8位元二進位制數為例，符號擴充套件的目標是將其轉換為16位元或32位元二進位制數，而保持數值不變。對於一個8位元正數二進位制數0111 1111，很容易得到正確的16位元結果0000 0000 0111 1111。但對於一個用二補數表示的負數，比如二補數1111 1111，我們該如何處理呢？我們只需要直接將其表示為16位元二進位制數1111 1111 1111 1111。換句話說，無論是正數還是二補數表示的負數，只需要在高位填充0或1即可。

總結

通過本文的學習，我們深入瞭解了計算機內部工作原理中的二進位制數、移位運算、補數表示、算術右移和邏輯右移等重要概念。我們瞭解到計算機底層使用二進位制來表示和處理資訊的原因，並學習了二進位制數的轉換方法和位權的概念。我們還探討了移位運算和二進位制數的運算，並介紹了移位運算在計算機中的應用。此外，我們學習了二進位制補數的概念和計算方法，以及符號擴充套件的原理和應用。最後，我們討論了算術右移和邏輯右移的區別，並總結了在左移和右移操作中應該採用的補位方法。通過本文的學習，我們對計算機內部工作原理有了更深入的瞭解，為進一步學習和研究電腦科學打下了堅實的基礎。