圖演演算法DFS與BFS

BFS和DFS代表對圖進行遍歷，即搜尋的演演算法，搜尋演演算法中常用的只要有兩種演演算法:深度優先遍歷(Depth-First-Search : DFS)和廣度優先遍歷(Breadth-First-Search : BFS)。一個圖結構可以用來表示大量現實生活中的問題，比如，道路網路，計算機網路，社群網路，使用者身份解析圖

①DFS深度優先搜尋樹

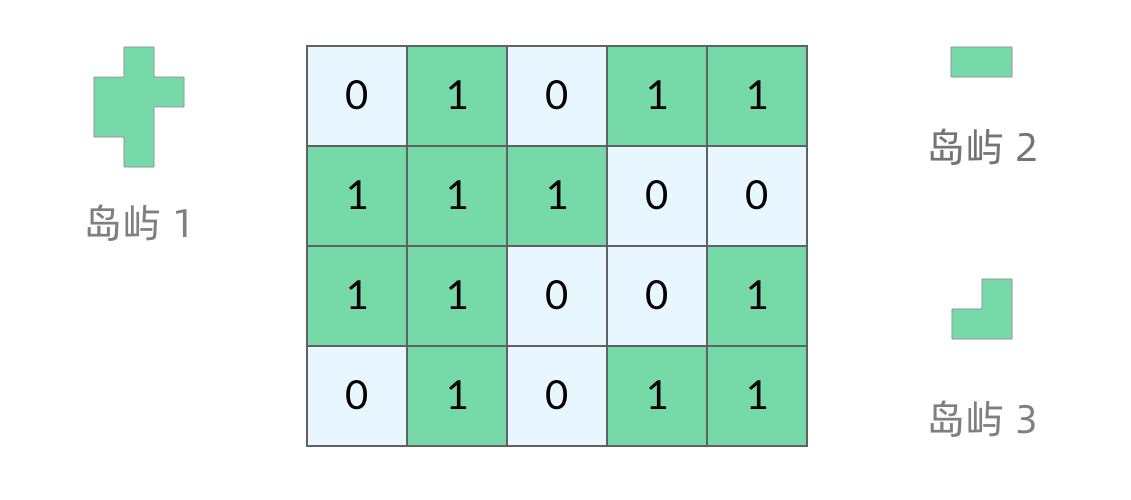
200. 島嶼數量

給你一個由 '1'（陸地）和 '0'（水）組成的的二維網格，請你計算網格中島嶼的數量。

島嶼總是被水包圍，並且每座島嶼只能由水平方向和/或豎直方向上相鄰的陸地連線形成。

此外，你可以假設該網格的四條邊均被水包圍。

範例 1：

輸入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
輸出：1

範例 2：

輸入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
輸出：3

如何在二維矩陣中使用 DFS 搜尋呢？

// 二維矩陣遍歷框架
void dfs(int[][] grid, int i, int j, boolean[][] visited) {
    int m = grid.length, n = grid[0].length;
     // 超出索引邊界
    if (i < 0 || j < 0 || i >= m || j >= n) {
        return;
    }
    // 已遍歷過 (i, j)
    if (visited[i][j]) {
        return;
    }
    // 進入節點 (i, j)
    visited[i][j] = true;
    dfs(grid, i - 1, j, visited); // 上
    dfs(grid, i + 1, j, visited); // 下
    dfs(grid, i, j - 1, visited); // 左
    dfs(grid, i, j + 1, visited); // 右
    visited[i][j] = false;
}

因為二維矩陣本質上是一幅「圖」，所以遍歷的過程中需要一個 visited 布林陣列防止走回頭路

目標是找到矩陣中「島嶼的數量」，即上下左右相連的 1 都被認為是連續島嶼。

演演算法步驟：每次遇到陸地計數器加1，並把該陸地和該陸地上下左右的陸地變為海水，遍歷完之後計數器就是島嶼數量

class Solution {
  // 主函數，計算島嶼數量
  int numIslands(char[][] grid) {
      int res = 0;
      int m = grid.length, n = grid[0].length;
      // 遍歷 grid
      for (int i = 0; i < m; i++) {
          for (int j = 0; j < n; j++) {
              if (grid[i][j] == '1') {
                  // 每發現一個島嶼，島嶼數量加一
                  res++;
                  // 然後使用 DFS 將島嶼淹了
                  dfs(grid, i, j);
              }
          }
      }
      return res;
  }

  // 從 (i, j) 開始，將與之相鄰的陸地都變成海水
  void dfs(char[][] grid, int i, int j) {
      int m = grid.length, n = grid[0].length;
      if (i < 0 || j < 0 || i >= m || j >= n) {
          // 超出索引邊界
          return;
      }
      if (grid[i][j] == '0') {
          // 已經是海水了
          return;
      }
      // 將 (i, j) 變成海水
      grid[i][j] = '0';
      // 淹沒上下左右的陸地
      dfs(grid, i + 1, j);
      dfs(grid, i, j + 1);
      dfs(grid, i - 1, j);
      dfs(grid, i, j - 1);
  }
}

為什麼每次遇到島嶼，都要用 DFS 演演算法把島嶼「淹了」呢？主要是為了省事，避免維護 visited 陣列。

因為 dfs 函數遍歷到值為 0 的位置會直接返回，所以只要把經過的位置都設定為 0，就可以起到不走回頭路的作用。

733. 影象渲染

面試題 08.10. 顏色填充 - 力扣（Leetcode）

有一幅以 m x n 的二維整數陣列表示的圖畫 image ，其中 image[i][j] 表示該圖畫的畫素值大小。

你也被給予三個整數 sr , sc 和 newColor 。你應該從畫素 image[sr][sc] 開始對影象進行上色填充。

為了完成 上色工作 ，從初始畫素開始，記錄初始座標的 上下左右四個方向上 畫素值與初始座標相同的相連畫素點，接著再記錄這四個方向上符合條件的畫素點與他們對應 四個方向上 畫素值與初始座標相同的相連畫素點，……，重複該過程。將所有有記錄的畫素點的顏色值改為 newColor 。

最後返回 經過上色渲染後的影象 。

範例 1:

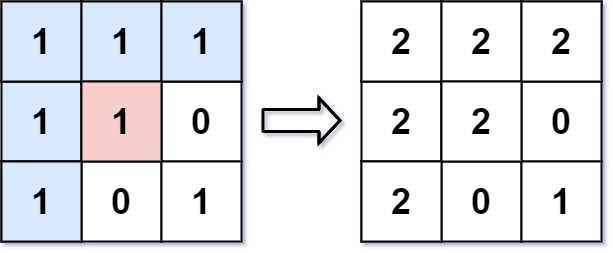
輸入: image = [[1,1,1],[1,1,0],[1,0,1]]，sr = 1, sc = 1, newColor = 2
輸出: [[2,2,2],[2,2,0],[2,0,1]]
解析: 在影象的正中間，(座標(sr,sc)=(1,1)),在路徑上所有符合條件的畫素點的顏色都被更改成2。
注意，右下角的畫素沒有更改為2，因為它不是在上下左右四個方向上與初始點相連的畫素點。

範例 2:

輸入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2
輸出: [[2,2,2],[2,2,2]]

class Solution {
    public int[][] floodFill(int[][] image, int sr, int sc, int color) {
        dfs(image, sr, sc, color, image[sr][sc]);
        return image;
    }
    public void dfs(int[][] image, int i, int j, int newColor, int oldColor){
        int m = image.length, n = image[0].length;
        // 超出邊界
        if(i < 0 || j < 0 || i >= m || j >= n) {
            return;
        }
        // 連續的初始值才染色
        if(image[i][j] != oldColor || newColor == oldColor){
            return;
        }
        // 染色
        image[i][j] = newColor;
        // 遍歷
        dfs(image, i - 1, j, newColor, oldColor);
        dfs(image, i + 1, j, newColor, oldColor);
        dfs(image, i, j - 1, newColor, oldColor);
        dfs(image, i, j + 1, newColor, oldColor); 

    }
}

1254. 統計封閉島嶼的數目

二維矩陣 grid 由 0 （土地）和 1 （水）組成。島是由最大的4個方向連通的 0 組成的群，封閉島是一個 完全 由1包圍（左、上、右、下）的島。

請返回 封閉島嶼 的數目。

範例 1：

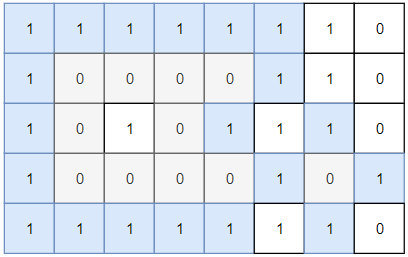
輸入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
輸出：2
解釋：
灰色區域的島嶼是封閉島嶼，因為這座島嶼完全被水域包圍（即被 1 區域包圍）。

範例 2：

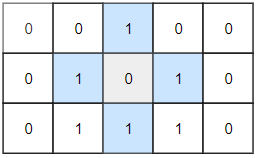
輸入：grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
輸出：1

範例 3：

輸入：grid = [[1,1,1,1,1,1,1],
           [1,0,0,0,0,0,1],
           [1,0,1,1,1,0,1],
           [1,0,1,0,1,0,1],
           [1,0,1,1,1,0,1],
           [1,0,0,0,0,0,1],
           [1,1,1,1,1,1,1]]
輸出：2

力扣第 200 題「島嶼數量」有兩點不同：

1、用 0 表示陸地，用 1 表示海水。

2、讓你計算「封閉島嶼」的數目。所謂「封閉島嶼」就是上下左右全部被 1 包圍的 0，也就是說靠邊的陸地不算作「封閉島嶼」。

那麼如何判斷「封閉島嶼」呢？其實很簡單，把第200題中那些靠邊的島嶼排除掉，剩下的不就是「封閉島嶼」了嗎？

class Solution {
    public int closedIsland(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        for(int j = 0; j < n; j++){
            dfs(grid, 0, j);  // 把靠上邊的島嶼淹掉
            dfs(grid, m - 1, j);  // 把靠下邊的島嶼淹掉
        }
        for(int i = 0; i < m; i++){
            dfs(grid, i, 0);  // 把靠上邊的島嶼淹掉
            dfs(grid, i, n - 1);  // 把靠下邊的島嶼淹掉
        }
        int res = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 0){
                    res++;
                    dfs(grid, i, j);
                }
            }
        }
        return res;
    }

    // 從 (i, j) 開始，將與之相鄰的陸地都變成海水
    public void dfs(int[][] grid, int i, int j) {
        int m = grid.length, n = grid[0].length;
        // 超出邊界
        if (i < 0 || j < 0 || i >= m || j >= n) {
            return;
        }
        // 已經是海水了
        if (grid[i][j] == 1) {
            return;
        }
        // 將 (i, j) 變成海水
        grid[i][j] = 1;
        // 淹沒上下左右的陸地
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);
    }
}

695. 島嶼的最大面積

劍指 Offer II 105. 島嶼的最大面積 - 力扣（Leetcode）

給你一個大小為 m x n 的二進位制矩陣 grid 。

島嶼是由一些相鄰的 1 (代表土地) 構成的組合，這裡的「相鄰」要求兩個 1 必須在 水平或者豎直的四個方向上 相鄰。你可以假設 grid 的四個邊緣都被 0（代表水）包圍著。

島嶼的面積是島上值為 1 的單元格的數目。

計算並返回 grid 中最大的島嶼面積。如果沒有島嶼，則返回面積為 0 。

範例 1：

img

輸入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
輸出：6
解釋：答案不應該是 11 ，因為島嶼只能包含水平或垂直這四個方向上的 1 。

範例 2：

輸入：grid = [[0,0,0,0,0,0,0,0]]
輸出：0

給 dfs 函數設定返回值，記錄每次淹沒的陸地的個數

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int max = 0; // 記錄島嶼的最大面積
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1){
                    // 淹沒島嶼，並更新最大島嶼面積
                    max = Math.max(max, dfs(grid, i, j));
                }
            }
        }
        return max;
    }
    // 淹沒與（i，j） 相鄰的陸地，並返回淹沒的陸地面積
    public int dfs(int[][] grid, int i, int j){
        int m = grid.length, n = grid[0].length;
        // 超出索引邊界
        if(i < 0 || j < 0 || i >= m || j >= n){
            return 0;
        }
        // 已經是海水
        if(grid[i][j] == 0){
            return 0;
        }
        // 將（i，j）變為海水
        grid[i][j] = 0;
        // 淹沒上下左右的陸地，並統計淹沒陸地數量
        int sum = 1; // 預設sum為1，如果不是島嶼，則直接返回0，就可以避免預防錯誤的情況。
        sum += dfs(grid, i - 1, j);
        sum += dfs(grid, i + 1, j);
        sum += dfs(grid, i, j - 1);
        sum += dfs(grid, i, j + 1);
        return sum;
    }
}

1020. 飛地的數量

給你一個大小為 m x n 的二進位制矩陣 grid ，其中 0 表示一個海洋單元格、1 表示一個陸地單元格。

一次移動是指從一個陸地單元格走到另一個相鄰（上、下、左、右）的陸地單元格或跨過 grid 的邊界。

返回網格中無法在任意次數的移動中離開網格邊界的陸地單元格的數量。

範例 1：

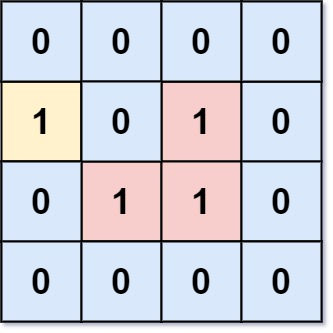
輸入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
輸出：3
解釋：有三個 1 被 0 包圍。一個 1 沒有被包圍，因為它在邊界上。

範例 2：

img

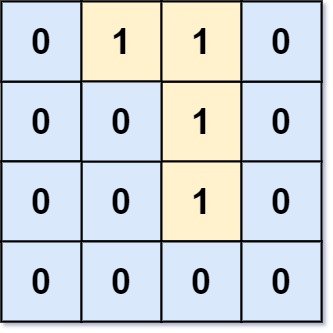
輸入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
輸出：0
解釋：所有 1 都在邊界上或可以到達邊界。

class Solution {
    public int numEnclaves(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        // 去除上下邊界陸地
        for(int j = 0; j < n; j++){
            dfs(grid, 0, j);
            dfs(grid, m - 1, j);
        }
        // 去除左右邊界陸地
        for(int i = 0; i < m; i++){
            dfs(grid, i, 0);
            dfs(grid, i, n - 1);
        }
        int res = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j]== 1){
                    res++;
                }
            }
        }
        return res;
        
    }
    // 從 (i, j) 開始，將與之相鄰的陸地都變成海水
    public void dfs(int[][] grid, int i, int j) {
        int m = grid.length, n = grid[0].length;
        // 超出邊界
        if (i < 0 || j < 0 || i >= m || j >= n) {
            return;
        }
        // 已經是海水了
        if (grid[i][j] == 0) {
            return;
        }
        // 將 (i, j) 變成海水
        grid[i][j] = 0;
        // 淹沒上下左右的陸地
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);
    }
}


class Solution {
    public int numEnclaves(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        // 去除上下邊界陸地
        for(int j = 0; j < n; j++){
            dfs(grid, 0, j);
            dfs(grid, m - 1, j);
        }
        // 去除左右邊界陸地
        for(int i = 0; i < m; i++){
            dfs(grid, i, 0);
            dfs(grid, i, n - 1);
        }
        int res = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j]== 1){
                    res += dfs(grid, i, j);
                }
            }
        }
        return res;
        
    }

    // 淹沒與（i，j） 相鄰的陸地，並返回淹沒的陸地面積
    public int dfs(int[][] grid, int i, int j){
        int m = grid.length, n = grid[0].length;
        // 超出邊界
        if(i < 0 || j < 0 || i >= m || j >= n){
            return 0;
        }
        // 已是海水
        if(grid[i][j] == 0){
            return 0;
        }
        // 將（i，j）變為海水
        grid[i][j] = 0;
        // 淹沒上下左右的陸地，並統計淹沒陸地數量
        int sum = 1;
        sum += dfs(grid, i + 1, j);
        sum += dfs(grid, i, j + 1);
        sum += dfs(grid, i - 1, j);
        sum += dfs(grid, i, j - 1);
        return sum;
    }
}

噪音傳播-華為數存面試

噪音傳播-題解

終端產品在進行一項噪音監測實驗。若將空實驗室平面圖視作一個N*M的二維矩陣（左上角為[0,0]）。工作人員在實驗室內設定了若干噪音源，並以[噪音源所在行，噪音源所在列，噪音值]的形式記錄於二維陣列noise中。
噪音沿相鄰8個方向傳播，在傳播過程中，噪音值（單位為分貝）逐級遞減1分貝，直至分貝削弱至1（即噪音源覆蓋區域邊緣噪音分貝為1）;
若同一格被多個噪音源的噪音覆蓋，檢測結果不疊加，僅保留較大的噪音值（噪音源所在格也可能被其他噪音源的噪聲傳播所覆蓋）。
在所有噪音源開啟且持續傳播情況穩定後，請監測每格噪音分貝數並返回他們的總和。

注意：
除噪音源以外的所有格初始值為0分貝；不考慮牆面反射。

範例1：

輸入：n=5,m=6,noise=[[3,4,3],[1,1,4]]
輸出：63

class Main {
    public static void main(String[] args) {
                int[][] noise = {{3,4,3}, {1,1,4}};
        System.out.println(spreadNoise(5, 6, noise));
    }

    public static int spreadNoise(int n, int m, int[][] noise) {
        int[][] grid = new int[n][m];
        for (int[] num: noise) {
            dfs(grid, num[0], num[1], num[2]);
        }
        // 統計結果
        int sum = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                sum += grid[i][j];
            }
        }
        return sum;
    }

    // 噪聲填充
    // 將（i，j）的 8 個方向填充資料
    public static void dfs(int[][] grid, int row, int col, int val){
        int m = grid.length, n = grid[0].length;
        // 超出邊界
        if (row < 0 || col < 0 || row >= m || col >= n) {
            return;
        }
        // 迴圈結束（val為0 或 保留較大的噪音值）
        if (val == 0 || grid[row][col] >= val) {
            return;
        }
        // 記錄值
        grid[row][col] = val;
        // 沿8個方向擴散
        dfs(grid, row + 1, col, val - 1);
        dfs(grid, row - 1, col, val - 1);
        dfs(grid, row, col + 1, val - 1);
        dfs(grid, row, col - 1, val - 1);
        dfs(grid, row + 1, col + 1, val - 1);
        dfs(grid, row + 1, col - 1, val - 1);
        dfs(grid, row - 1, col + 1, val - 1);
        dfs(grid, row - 1, col - 1, val - 1);
    }
}

79. 單詞搜尋

給定一個 m x n 二維字元網格 board 和一個字串單詞 word 。如果 word 存在於網格中，返回 true ；否則，返回 false 。

單詞必須按照字母順序，通過相鄰的單元格內的字母構成，其中「相鄰」單元格是那些水平相鄰或垂直相鄰的單元格。同一個單元格內的字母不允許被重複使用。

進階：你可以使用搜尋剪枝的技術來優化解決方案，使其在 board 更大的情況下可以更快解決問題？

範例 1：

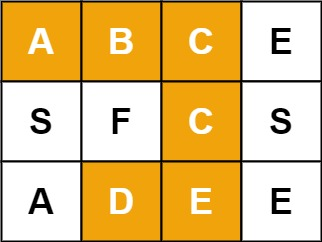
輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
輸出：true

範例 2：

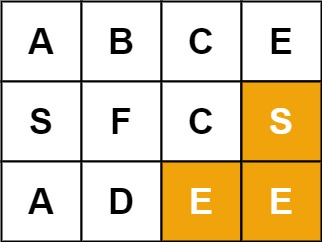
輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
輸出：true

範例 3：

輸入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
輸出：false

class Solution {
    public boolean exist(char[][] board, String word) {
        int m = board.length, n = board[0].length;
        boolean[][] visited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if(dfs(board, i, j, word, 0, visited)){
                     return true;
                 }
            }
        }
        return false;
    }

    // 從 (i, j) 開始向四周搜尋，試圖匹配 word[p..]
    boolean dfs(char[][] board, int i, int j, String word, int p, boolean[][] visited) {
        int m = board.length, n = board[0].length;
        if(p == word.length()){
            return true;
        }
        if (i < 0 || j < 0 || i >= m || j >= n) {
            // 超出索引邊界
            return false;
        }
        if(board[i][j] != word.charAt(p)){
            return false;
        }
        if (visited[i][j]) {
            // 已遍歷過 (i, j)
            return false;
        }
        // 進入節點 (i, j)
        visited[i][j] = true;
        boolean t = dfs(board, i - 1, j, word, p + 1, visited); // 上
        boolean b = dfs(board, i + 1, j, word, p + 1, visited); // 下
        boolean l = dfs(board, i, j - 1, word, p + 1, visited); // 左
        boolean r = dfs(board, i, j + 1, word, p + 1, visited); // 右
        visited[i][j] = false;
        return t || b || l || r;
    }
}

994. 腐爛的橘子

在給定的 m x n 網格 grid 中，每個單元格可以有以下三個值之一：

值 0 代表空單元格；
值 1 代表新鮮橘子；
值 2 代表腐爛的橘子。

每分鐘，腐爛的橘子 周圍 4 個方向上相鄰 的新鮮橘子都會腐爛。

返回 直到單元格中沒有新鮮橘子為止所必須經過的最小分鐘數。如果不可能，返回 -1 。

範例 1：

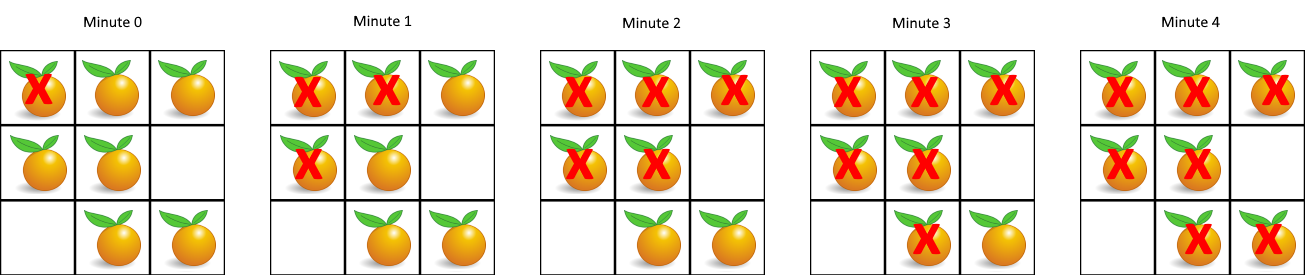
輸入：grid = [[2,1,1],[1,1,0],[0,1,1]]
輸出：4

範例 2：

輸入：grid = [[2,1,1],[0,1,1],[1,0,1]]
輸出：-1
解釋：左下角的橘子（第 2 行， 第 0 列）永遠不會腐爛，因為腐爛只會發生在 4 個正向上。

範例 3：

輸入：grid = [[0,2]]
輸出：0
解釋：因為 0 分鐘時已經沒有新鮮橘子了，所以答案就是 0 。

對於二維網格 grid 來說，當遍歷到腐爛的

JAVA圖搜尋演演算法之DFS-BFS

圖演演算法DFS與BFS

①DFS深度優先搜尋樹

200. 島嶼數量

733. 影象渲染

1254. 統計封閉島嶼的數目

695. 島嶼的最大面積

1020. 飛地的數量

噪音傳播-華為數存面試

79. 單詞搜尋

994. 腐爛的橘子