廣義字尾自動機（廣義 SAM）學習筆記

開 CF 開到了一道廣義 SAM，決定來學一學。
發現網上確實充斥著各種各樣的偽廣義 SAM，也看到了前人反覆修改假板子的過程，所以試著來整理一下這堆奇奇怪怪的問題。
當然本文的程式碼也不保證百分百正確，有誤請指出（？

前置知識

字尾自動機 (SAM) 的構造及應用
其實想寫在一起的，但因為太長就把這兩篇文章拆開了。本文所述的「上文」若無法在本文中找到，則均指代該部落格。

概述

廣義 SAM 用於解決多模式串上的子串相關問題。
它對多個字串建立出一個 SAM，或者說本質是對多個字串形成的一棵 Trie 樹建立 SAM。
其實大部分能夠使用普通 SAM 解決的字串問題都可以擴充套件到 Trie 樹上，並使用廣義 SAM 處理。

這裡要注意，題目給出多個字串和直接給出一棵 Trie 樹是不同的。後者僅保證了 Trie 樹的節點數，但沒有保證所有模式串的總長度。
設 \(n\) 為 Trie 的節點數，這種情況下的字串總長上界可以達到 \(n^2\)，可以通過在一條鏈的鏈底掛一個菊花構造得到。
一些廣義 SAM 寫法的時間複雜度基於字串總長而非節點個數，但第二種給出字串的方式遠不如第一種常見。因此這些寫法也是正確的廣義 SAM，只不過不適用於少量直接給出 Trie 的題目。
我們定義後文中與時間複雜度相關的部分，Trie 的節點數為 \(n\)，字串總長為 \(m\)。

定義與概念的拓展

在把 SAM 搬到 Trie 上之前，我們要先把單串 SAM 相關的定義拓展到 Trie 上。

字尾

首先定義 Trie 樹為 \(S\)，\(S_{x,y}\) 表示 Trie 上從點 \(x\) 到點 \(y\) 的路徑組成的字串。
那麼它的所有字尾可以表示為 \(\{S_{x,y} \mid y\in \text{subtree}(x), y \text{ is leaf}\}\)。
廣義 SAM 壓縮的就是該集合內的字尾。

endpos 集合

更改了字尾的定義，一個字串 \(\text{endpos}\) 集合的定義也隨之改變：\(\text{endpos}(t)=\{y\mid y\in \text{subtree}(x),S_{x,y}=t\}\)。

字尾連結 link

在新的 \(\text{endpos}\) 定義下，可以沿用字尾連結 \(\text{link}\) 的原定義。

那麼我們根據新的定義對 Trie 構建出的 SAM 結構，就可以稱作廣義 SAM。

常見的偽廣義 SAM

對於此類問題，通常有這樣幾種做法：

1. 在每兩個串之間新增一個特殊字元，把所有串連線成一個大串，再對其建單串 SAM。
2. 每次新增一個新串前將 \(lst\) 改為 \(1\)（初始節點），在原 SAM 的基礎上繼續構建。
3. 廣義 SAM。

但前兩種都是常見的偽廣義 SAM，我們依次對它們的正確性進行分析。

連成一個串建 SAM

結論：僅在字串個數很少時能夠保證複雜度。
這樣做可以解決一部分問題，例如前文所述 SAM 的最後一個例題 LCS2 - Longest Common Substring II。
但這種方法的瓶頸在於所有的「特殊字元」兩兩不能相同，否則不能對不同的子串進行區分。這造成了當題目僅保證字串總長而不保證個數時，將會需要大量的特殊字元。而 SAM 的線性複雜度是基於字元集大小為常數這一條件的。
因此這種方法造成了 SAM 的字元集不再為常數，時間複雜度無法保證。對於此題，可以這麼做是因為題目保證了字串數量不超過 \(10\)。

每次將 lst 置為 1

結論：時間複雜度正確，但會出現存在空節點的問題。
在字串總長有保證時，我們可以類比單串 SAM 的證明方法來證明它的線性複雜度。
但這種做法會出現所謂的「空節點」問題，這也是各種寫假的廣義 SAM 的共同錯誤。
由於該方法幾乎不需要對單串 SAM 進行改動，比較好寫，在很多不會出現正確性問題的題目中經常被使用。

故上述兩種方法都有其侷限性，學習正確的廣義 SAM 是必要的。

空節點問題

上文說過，各種寫假的廣義 SAM 會出現空節點。
先以已經提到的每次將 \(lst\) 置為 \(0\) 為例，看看為什麼會這樣。
舉一個簡單的例子，假設我們已經對 \(\mathtt{ab}\) 構建了 SAM：

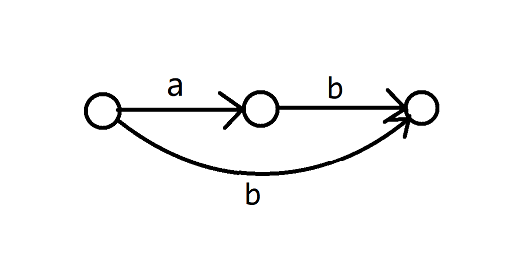
現在加入字串 \(\mathtt{b}\)，你會發現你新建了一個節點，把它的 \(\text{link}\) 連向了 \(0\)（藍色是 \(\text{link}\) 邊），但實際上沒有任何一條轉移邊連向它。

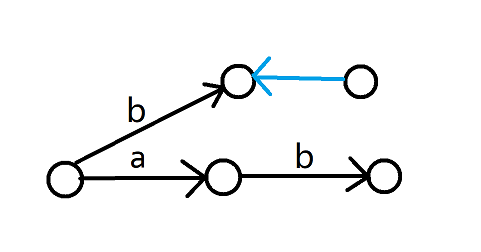
這樣的空節點在匹配子串時不會影響正確性，也不影響時間複雜度，僅作為一個自動機而言並沒有問題。
但它破壞了 SAM 用最小的狀態數儲存所有子串的性質，會影響到 \(fail\) 樹的子樹 \(siz\) 計算，在某些需要用到相關資訊的題目中出現錯誤。
下文會對各種本身正確但由於實現問題造成的假廣義 SAM 也給出分析。

bfs 離線構建

離線構建是指我們先讀入所有字串，對它們構建出 Trie 樹，再基於 Trie 樹構建 SAM 的寫法，分為 dfs 與 bfs 兩種實現方式。

bfs 實現

首先我們要做的事情是對字串建出 Trie。

struct trie{int fa,c,s[26];} tr[N];
int idx=1;
il void ins(char *s) 
{
    int len=strlen(s+1),now=1;
    for(int i=1;i<=len;i++) 
    {
        int &to=tr[now].s[s[i]-'a'];
        if(!to) to=++idx,tr[to].fa=now,tr[to].c=s[i]-'a'; now=to;
    }
}

然後考慮 SAM 的構造。因為每次是把父親節點在 SAM 上的位置作為 \(lst\) 構建新的節點，我們需要對每個 Trie 上的節點記錄它在 SAM 上對應的節點編號。

我們令點 \(x\) 在 SAM 上對應的節點編號為 \(pos_x\)。同時，為方便記錄這個 \(pos\)，我們對 insert 函數稍作改動，給它加上返回值，返回新新增的節點編號：

il int insert(int c,int lst)
{
    int p=lst,np=lst=++tot; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return np;
}

那麼我們 bfs 到點 \(x\) 時，把 \(pos_{fa_x}\) 作為 \(lst\)，向 SAM 插入 \(fa_x\) 到 \(x\) 這條邊上的字元 \(c\)，並令 \(pos_x\) 為 insert 函數的返回值即可。
由此可以寫出 bfs 的離線構建：

int pos[N];
il void build()
{
    queue<int> q;
    for(int i=0;i<26;i++) if(tr[1].s[i]) q.push(tr[1].s[i]);
    pos[1]=1;
    while(!q.empty())
    {
        int u=q.front(); q.pop();
        pos[u]=insert(tr[u].c,pos[tr[u].fa]);
        for(int i=0;i<26;i++) if(tr[u].s[i]) q.push(tr[u].s[i]);
    }
}

如果不考慮空節點問題，每次將 \(lst\) 置為 \(0\) 的方法是比較容易理解的。
而離線 bfs 構造實際上就是通過 Trie 樹的性質壓縮了原來的多個字串，這樣做相同的字首不再需要多次插入，其餘的和上面的方法本質相同。

為什麼 bfs 不會有空節點

考慮上面的做法出現了空節點是哪裡的問題。
我們在 \(lst\) 已經有一條 \(c\) 的轉移邊的情況下，試圖再給 \(lst\) 連新的 \(c\) 邊，就會出現加了一個節點，但加的轉移都跑到了原來 \(lst\) 連向的那個點。這個新加的點就變成了只有 \(\text{link}\) 的空殼。
而 bfs 的過程不同，它是按照字串的長度從小到大一層層加點的。也就是說，我們試圖給 \(fa_x\) 加一個 \(c\) 的轉移的時候，它之前不可能已經有一個 \(c\) 邊。
這個可以反證，如果 \(fa_x\) 已經有連向 \(c\) 的轉移，說明 \(fa_x\) 已經有一個邊為字元 \(c\) 的兒子。顯然合法的 Trie 中，一個節點不會有邊上字元相同的兩個不同兒子，故該情況不成立。
綜上，不在 insert 函數中加特判的 bfs 寫法是正確的，因為它保證了不會出現空點。

時間複雜度證明

bfs 寫法的時間複雜度為 \(O(n)\)，即 Trie 的節點數。
這是因為 bfs 的性質保證了 SAM 原有的時間複雜度證明仍然成立，參見前文 SAM 的複雜度證明。

dfs 離線構建

錯誤的 dfs 實現

我們似乎可以用同樣的方式來實現 dfs 離線構建，寫出如下的程式碼。

int pos[N];
il void dfs(int u)
{
    for(int i=0;i<26;i++)
    {
        int v=tr[u].s[i];
        if(v) pos[v]=insert(i,pos[u]),dfs(v);
    }
}

但這種不加任何特判的 dfs 寫法是錯的。在模板題增加輸出節點個數的要求後，它甚至無法通過樣例。

為什麼 dfs 會產生空節點

之前我們證明了 bfs 的正確性，為什麼換成 dfs 就錯了呢？
回想一下，我們的正確性證明是基於 「試圖給 \(fa_x\) 加一個 \(c\) 的轉移的時候，它之前不可能已經有一個 \(c\) 邊」 這條 bfs 獨有的性質的。
dfs 時顯然沒有這條保證，因此會和 \(lst\) 置為 \(0\) 的做法出一樣的問題。

更直觀但不那麼嚴謹的理解是，假設我們對 \(\mathtt{ab}\) 和 \(\mathtt{b}\) 建 Trie 然後 dfs，你會發現 Trie 建了個寂寞，它的演演算法過程跟 \(lst\) 置為 \(1\) 沒有任何本質區別。

正確的 dfs 實現

我們需要通過特判已有轉移邊的情況來規避以上問題。

il int insert(int c,int lst)
{
    if(d[lst].s[c]&&d[d[lst].s[c]].len==d[lst].len+1) {return d[lst].s[c];} //1
    int p=lst,np=++tot,flag=0; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    if(p==lst) flag=1,np=0,tot--;  //2
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return flag?nq:np;  //3
}

注意到，這份程式碼的 insert 過程和原來的區別是新增了註釋處的三句特判。接下來對它們依次進行解釋。

if(d[lst].s[c]&&d[d[lst].s[c]].len==d[lst].len+1) {return d[lst].s[c];} //1

這句話特判的是新加的串已經作為原來的子串出現過的情況，即 \(lst\) 已經有一條 \(c\) 的轉移，而且這個轉移是連續的。
此時我們什麼也不用做，新加入的點所在的 \(pos\) 就是當前 \(lst\) 連邊指向的點。

if(p==lst) flag=1,np=0,tot--;  //2

另外一種會出現空節點的情況是 \(lst\) 有 \(c\) 的轉移，但這個轉移不是連續的。
這表明在加入字元 \(c\) 後，應當有一部分字尾被拆出來變成新的狀態，但我們只應新建這個新狀態的節點，不應新建 \(lst\) 連向 \(c\) 的節點。還是以文章開頭那兩個字串為例。

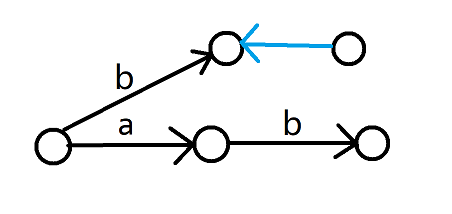
我們在插入第二個串時就是特判 2 的情況，這時候不應該新建一個節點。但是貌似我們在做這個判斷前已經新建過了。不過好在 \(np\) 裡面啥都沒有，把加過的 \(tot\) 減回去就好啦 qwq。
同時因為沒有新建節點，也不應該有 \(np\)，更不應該有 \(\text{link}(np)\)。所以為了避免後面意外修改這個位置的值，要把 \(np\) 置為 \(0\)。（我的 SAM 板子是從 \(1\) 開始編號，\(0\) 號節點沒有任何作用。）

return flag?nq:np;  //3

這句是容易理解的，沒有新建 \(np\) 但新建了 \(nq\)，就返回 \(nq\)。

至此我們寫出了正確的離線 dfs 板子。

dfs 的複雜度證明

與 bfs 做法不同，dfs 做法時間複雜度是 \(O(m)\)，即字串總長度。它不能用於直接給出 Trie 樹的題目。
這是因為我們原來在證 SAM 複雜度時的條件不適用了，SAM 每次都會在原來的 \(lst\) 後面加節點，並從 \(lst\) 開始跳 \(\text{link}\) 樹。這保證了被重定向的邊不會再次被重定向。
而 dfs 的過程中並沒有這樣的保證，一條邊可以隨著多個字串的加入被重定向多次。

舉一個直觀的例子，我們有這樣一棵 Trie：

現在 dfs 完了點 \(1\sim 5\)，獲得了一個長這樣的 SAM：

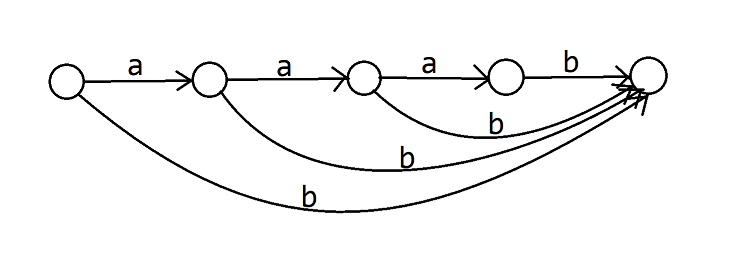
然後我們 dfs 點 \(6\)，發現它改變了 \(\mathtt{b,ab,aab}\) 的 \(\text{endpos}\) 集合，這些轉移都需要拆出來。

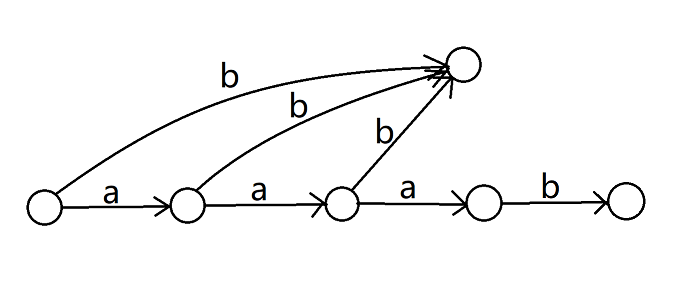
再繼續 dfs 點 \(7\)，又改變了 \(\mathtt{b,ab}\) 的 \(\text{endpos}\)，需要把之前拆出來過的轉移再拆出來：

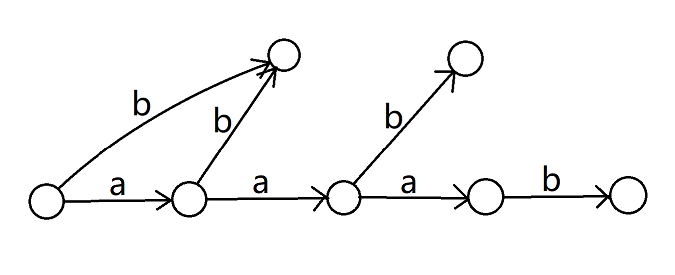
可以看出它的時間複雜度並不是 Trie 樹的節點數，因此 Trie 的結構對 dfs 的複雜度沒有什麼優化作用。
稍加思考的話，可以發現這樣的做法和每次把 \(lst\) 置為 \(1\)，再跑加特判版本的 SAM 沒有本質區別。它的時間複雜度是字串總長。

線上構建

線上構建廣義 SAM，就是不預先建出 Trie 樹，直接每次將 \(lst\) 置為 \(1\)，依次線上插入字串。
之前所說的錯誤做法是指不帶任何特判的 SAM，而我們在 dfs 中已經為 insert 函數增加了保證它不出現問題的特判。
那麼我們還要 dfs 幹什麼呢？直接用這個加過特判的 insert 函數線上構造，重複的字首會被特判處理到，其實就變成對的了。它的時間複雜度是字串總長 \(O(m)\)。

至此我們介紹完了廣義 SAM 常見的離線和線上寫法。

應用

在實際應用中，SAM 的大部分結論在廣義 SAM 中依然成立。

P6139 【模板】廣義字尾自動機（廣義 SAM）

回到本題。根據 SAM 的已有結論，每個節點包含的不同子串數為 \(\text{len}(x)-\text{len}(\text{link}(x))\)。
所以構建出廣義 SAM 後統計答案即可。

離線 bfs 版

#include<bits/stdc++.h>
#define il inline
using namespace std;
il long long read()
{
    long long xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9')
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=2e6+5;
struct trie{int fa,c,s[26];} tr[N];
int idx=1;
il void ins(char *s) 
{
    int len=strlen(s+1),now=1;
    for(int i=1;i<=len;i++) 
    {
        int &to=tr[now].s[s[i]-'a'];
        if(!to) to=++idx,tr[to].fa=now,tr[to].c=s[i]-'a'; now=to;
    }
}
struct SAM{int fa,len,s[26];} d[N];
int tot=1;
il int insert(int c,int lst)
{
    int p=lst,np=lst=++tot; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return np;
}
int pos[N];
il void build()
{
    queue<int> q;
    for(int i=0;i<26;i++) if(tr[1].s[i]) q.push(tr[1].s[i]);
    pos[1]=1;
    while(!q.empty())
    {
        int u=q.front(); q.pop();
        pos[u]=insert(tr[u].c,pos[tr[u].fa]);
        for(int i=0;i<26;i++) if(tr[u].s[i]) q.push(tr[u].s[i]);
    }
}
char s[N];
int main()
{
    int n=read();
    for(int i=1;i<=n;i++) scanf("%s",s+1),ins(s);
    build();
    long long ans=0;
    for(int i=2;i<=tot;i++) ans+=d[i].len-d[d[i].fa].len;
    printf("%lld\n%d\n",ans,tot);
    return 0;
}

離線 dfs 版

#include<bits/stdc++.h>
#define il inline
using namespace std;
il long long read()
{
    long long xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9')
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=2e6+5;
struct trie{int fa,c,s[26];} tr[N];
int idx=1;
il void ins(char *s) 
{
    int len=strlen(s+1),now=1;
    for(int i=1;i<=len;i++) 
    {
        int &to=tr[now].s[s[i]-'a'];
        if(!to) to=++idx,tr[to].fa=now,tr[to].c=s[i]-'a'; now=to;
    }
}
struct SAM{int fa,len,s[26];} d[N];
int tot=1;
il int insert(int c,int lst)
{
    if(d[lst].s[c]&&d[d[lst].s[c]].len==d[lst].len+1) {return d[lst].s[c];}
    int p=lst,np=++tot,flag=0; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    if(p==lst) flag=1,np=0,tot--;
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return flag?nq:np;
}
int pos[N];
il void dfs(int u)
{
    for(int i=0;i<26;i++)
    {
        int v=tr[u].s[i];
        if(v) pos[v]=insert(i,pos[u]),dfs(v);
    }
}
char s[N];
int main()
{
    int n=read();
    for(int i=1;i<=n;i++) scanf("%s",s+1),ins(s);
    pos[1]=1,dfs(1);
    long long ans=0;
    for(int i=2;i<=tot;i++) ans+=d[i].len-d[d[i].fa].len;
    printf("%lld\n%d\n",ans,tot);
    return 0;
}

線上版

#include<bits/stdc++.h>
#define il inline
using namespace std;
il long long read()
{
    long long xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9')
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=2e6+5;
struct SAM{int fa,len,s[26];} d[N];
int tot=1,pos[N];
il int insert(int c,int lst)
{
    if(d[lst].s[c]&&d[d[lst].s[c]].len==d[lst].len+1) {return d[lst].s[c];} 
    int p=lst,np=++tot,flag=0; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    if(p==lst) flag=1,np=0,tot--;  
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return flag?nq:np;  
}
char s[N];
int main()
{
    int n=read();
    for(int i=1;i<=n;i++) 
    {
        scanf("%s",s+1);
        int len=strlen(s+1); pos[0]=1;
        for(int j=1;j<=len;j++) pos[j]=insert(s[j]-'a',pos[j-1]);
    }
    long long ans=0;
    for(int i=2;i<=tot;i++) ans+=d[i].len-d[d[i].fa].len;
    printf("%lld\n%d\n",ans,tot);
    return 0;
}

其他例題

待更新。

參考資料

• 《字尾自動機在字典樹上的拓展》by 劉研繹
• 【學習筆記】字串—廣義字尾自動機 by 辰星凌
• 悲慘故事 長文警告 關於廣義 SAM 的討論 by ix35

坑還沒填，但是先撒花 >w<