點集合的三角剖分

點集合的三角剖分是指如何將一些離散的點集合組合成不均勻的三角形網格，使得每個點成為三角網中三角面的頂點。這個演演算法的用處很多，一個典型的意義在於可以通過一堆離散點構建的TIN實現對整個構網區域的線性控制，比如用帶高程的離散點構建的TIN來表達地形。

在實際工作中，使用最多的三角剖分是Delaunay三角剖分。通過Delaunay三角剖分演演算法能夠構建一個具有空圓特性和最大化最小角特性的三角網。空圓特性其實就是對於兩個共邊的三角形，任意一個三角形的外接圓中都不能包含有另一個三角形的頂點，這種形式的剖分產生的最小角最大。這些特性可能有些難以理解，但是我們可以先謹記一點：Delaunay三角網是一種特性最優的三角剖分。

通過CGAL，我們可以直接通過離散點集生成Delaunay三角網，實現程式碼如下：

#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Projection_traits_xy_3.h>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Projection_traits_xy_3<K> Gt;
typedef CGAL::Delaunay_triangulation_2<Gt> Delaunay;
typedef K::Point_3 Point;

#include <ogrsf_frmts.h>

#include <iostream>
#include <string>

using namespace std;

bool ReadVector(vector<Point> &vertexList) {
  string srcFile = "Data/Vector/points.shp";

  GDALDataset *poDS = (GDALDataset *)GDALOpenEx(srcFile.c_str(), GDAL_OF_VECTOR,
                                                NULL, NULL, NULL);
  if (!poDS) {
    printf("無法讀取該檔案，請檢查資料是否存在問題！");
    return false;
  }

  if (poDS->GetLayerCount() < 1) {
    printf("該檔案的層數小於1，請檢查資料是否存在問題！");
    return false;
  }

  for (int li = 0; li < poDS->GetLayerCount(); li++) {
    OGRLayer *poLayer = poDS->GetLayer(li);  //讀取層
    poLayer->ResetReading();

    //遍歷特徵
    OGRFeature *poFeature = nullptr;
    while ((poFeature = poLayer->GetNextFeature()) != nullptr) {
      OGRGeometry *geometry = poFeature->GetGeometryRef();
      OGRwkbGeometryType geometryType = geometry->getGeometryType();

      switch (geometryType) {
        case wkbPoint:
        case wkbPointM:
        case wkbPointZM: {
          OGRPoint *ogrPoint = dynamic_cast<OGRPoint *>(geometry);
          if (ogrPoint) {
            vertexList.emplace_back(ogrPoint->getX(), ogrPoint->getY(), 0);
          }
          break;
        }
        case wkbMultiPoint:
        case wkbMultiPointM:
        case wkbMultiPointZM: {
          OGRMultiPoint *ogrMultiPoint =
              dynamic_cast<OGRMultiPoint *>(geometry);
          if (!ogrMultiPoint) {
            continue;
          }

          for (int gi = 0; gi < ogrMultiPoint->getNumGeometries(); gi++) {
            OGRPoint *ogrPoint =
                dynamic_cast<OGRPoint *>(ogrMultiPoint->getGeometryRef(gi));
            if (ogrPoint) {
              vertexList.emplace_back(ogrPoint->getX(), ogrPoint->getY(), 0);
            }
          }

          break;
        }
        default: {
          printf("未處理的特徵型別\n");
          break;
        }
      }

      OGRFeature::DestroyFeature(poFeature);
    }
  }

  GDALClose(poDS);
  poDS = nullptr;

  return true;
}

bool WriteVector(const Delaunay &dt) {
  string dstFile = "Data/Out.shp";

  GDALDriver *driver =
      GetGDALDriverManager()->GetDriverByName("ESRI Shapefile");
  if (!driver) {
    printf("Get Driver ESRI Shapefile Error！\n");
    return false;
  }

  GDALDataset *dataset =
      driver->Create(dstFile.c_str(), 0, 0, 0, GDT_Unknown, NULL);
  OGRLayer *poLayer = dataset->CreateLayer("tin", NULL, wkbPolygon, NULL);

  //建立面要素
  for (const auto &f : dt.finite_face_handles()) {
    OGRFeature *poFeature = new OGRFeature(poLayer->GetLayerDefn());

    OGRLinearRing ogrring;
    for (int i = 0; i < 3; i++) {
      ogrring.setPoint(i, f->vertex(i)->point().x(), f->vertex(i)->point().y());
    }
    ogrring.closeRings();

    OGRPolygon polygon;
    polygon.addRing(&ogrring);
    poFeature->SetGeometry(&polygon);

    if (poLayer->CreateFeature(poFeature) != OGRERR_NONE) {
      printf("Failed to create feature in shapefile.\n");
      return false;
    }
  }

  //釋放
  GDALClose(dataset);
  dataset = nullptr;

  return true;
}

int main() {
  GDALAllRegister();
  CPLSetConfigOption("GDAL_FILENAME_IS_UTF8", "NO");  //支援中文路徑
  CPLSetConfigOption("SHAPE_ENCODING", "");           //解決中文亂碼問題

  vector<Point> vertexList;
  ReadVector(vertexList);

  Delaunay dt(vertexList.begin(), vertexList.end());

  WriteVector(dt);
  return 0;
}

這裡我們先從一個向量中讀取了離散點集，在QGIS中顯示如下圖4.21所示：

在程式最後，將生成的Delaunay三角網輸出成另外一個向量檔案，在QGIS中顯示如下圖4.22所示：

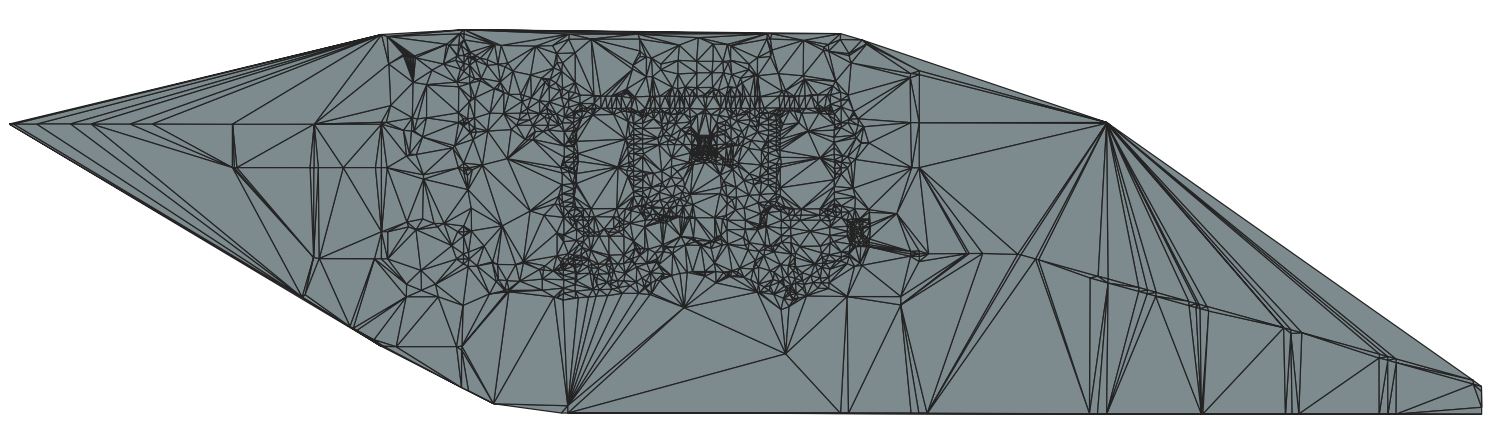
讀取和寫出比較好理解，關鍵是呼叫CGAL進行構建Delaunay三角網，其實相當簡短：

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Projection_traits_xy_3<K> Gt;
typedef CGAL::Delaunay_triangulation_2<Gt> Delaunay;
typedef K::Point_3 Point;

int main() {
{
  //...
  vector<Point> vertexList;
  //...
  Delaunay dt(vertexList.begin(), vertexList.end());
  //...
}

CGAL大量應用了C++的模板（泛型）技術，因而使用的介面比較抽象可能難以理解，這裡可以解釋一下CGAL的設計邏輯。學過任何一門程式語言的都知道，浮點型數值的相等判斷不能直接使用相等運運算元；正確的做法是使用兩者相減的絕對值與容差進行判斷，因為計算機表達的浮點型是個近似值。計算幾何的核心問題正在於此，內建資料型別的精度是有限的，處理容差是非常麻煩的事情。所以數值需要更為精確的表達，比如0.5就應該就是0.5，不能是0.49999999。因此CGAL確定了一個Kernel(核)的概念，通過模板來控制不同精度。

這裡的typedef CGAL::Exact_predicates_inexact_constructions_kernel K;表示精確謂詞，但不精確構造的核心。predicates(謂詞)表示一個操作；(constructions)構造意味著會有新的數值物件作為結果，如果演演算法是一個不進行構造的演演算法中，就可以使用精確謂詞但不精確構造的核心。比如這裡的構建Delaunay三角網，並沒有新的點物件生成出來，只是對點集進行了組織，點還是原來哪些點，並沒有變化。

另外，typedef K::Point_3 Point;表示我們使用該精度下的內建三維點型別。但是另外一個問題在於，如果我們需要定義三個維度中的哪兩個維度數值參與構網計算，或者使用自定義資料結構該怎麼辦呢？所以可以傳入Traits型別，這其實是C++的模板中的traits技術，描述了傳入資料的數值特性：比如型別，排序，方向測試或者相等判斷等。每個Kernel中都有定義好的Traits型別，這裡使用的就是typedef CGAL::Projection_traits_xy_3<K> Gt;,使用點的xy值參與構網計算。最後將該型別作為模板引數傳入到Delaunay三角網構建類中：typedef CGAL::Delaunay_triangulation_2<Gt> Delaunay;。

上述的解析讀者如果沒有一定的C++模板知識的基礎，肯定看的雲裡霧裡。其實不要緊，筆者也只是希望大家能夠理解CGAL如此設計介面的內在邏輯，並不是故意設計的如此抽象和繁瑣，而是希望最大程度的保證精度和效能。更多更具體的解析，讀者可以參看CGAL檔案。對C++模板知識不熟悉的初學者，建議直接參考檔案中的給出的範例，在實際使用過程中逐漸增加自己的認識。