原發表於個人部落格。

前言

線段樹，是資料結構皇冠上的明珠（我編的）。

它用途廣泛，被一代代的oier應用，改進，優化。

本文介紹了線段樹的基礎知識和各種拓展（包括權值線段樹，可持久化線段樹），各種優化方式（包括zkw線段樹，動態開點，離散化），希望能幫到更多的oier。

在學習線段樹前，預設你應該學會一下內容：

1. 樹和二元樹的基本知識（這你總得會吧）
2. 二元堆積（主要是堆式儲存）
3. 離散化（其實並不需要）
4. 會寫程式碼

如果你不會，左轉oiwiki，如果你會，那麼繼續讀吧！

線段樹的引入

舉個例子，我們現在有一個序列，想維護一段子區間的和，該怎麼辦呢？

你或許會說，可以暴力！把這個區間的數加起來就行了。

那麼如果這個子區間裡有1e5個數呢？

字首和？

如果強制線上呢？

如果在維護區間和的同時維護最大值、並且支援區間修改呢？

我們有很多種辦法維護區間問題，比如樹狀陣列，線段樹，分塊。其中，線段樹是較通用且直觀的一種資料結構。

基礎線段樹

線段樹入門

首先，我們有一個序列。

我們利用二分的思想，用每一個節點表示一個區間，兩個子節點表示左右兩個子區間。

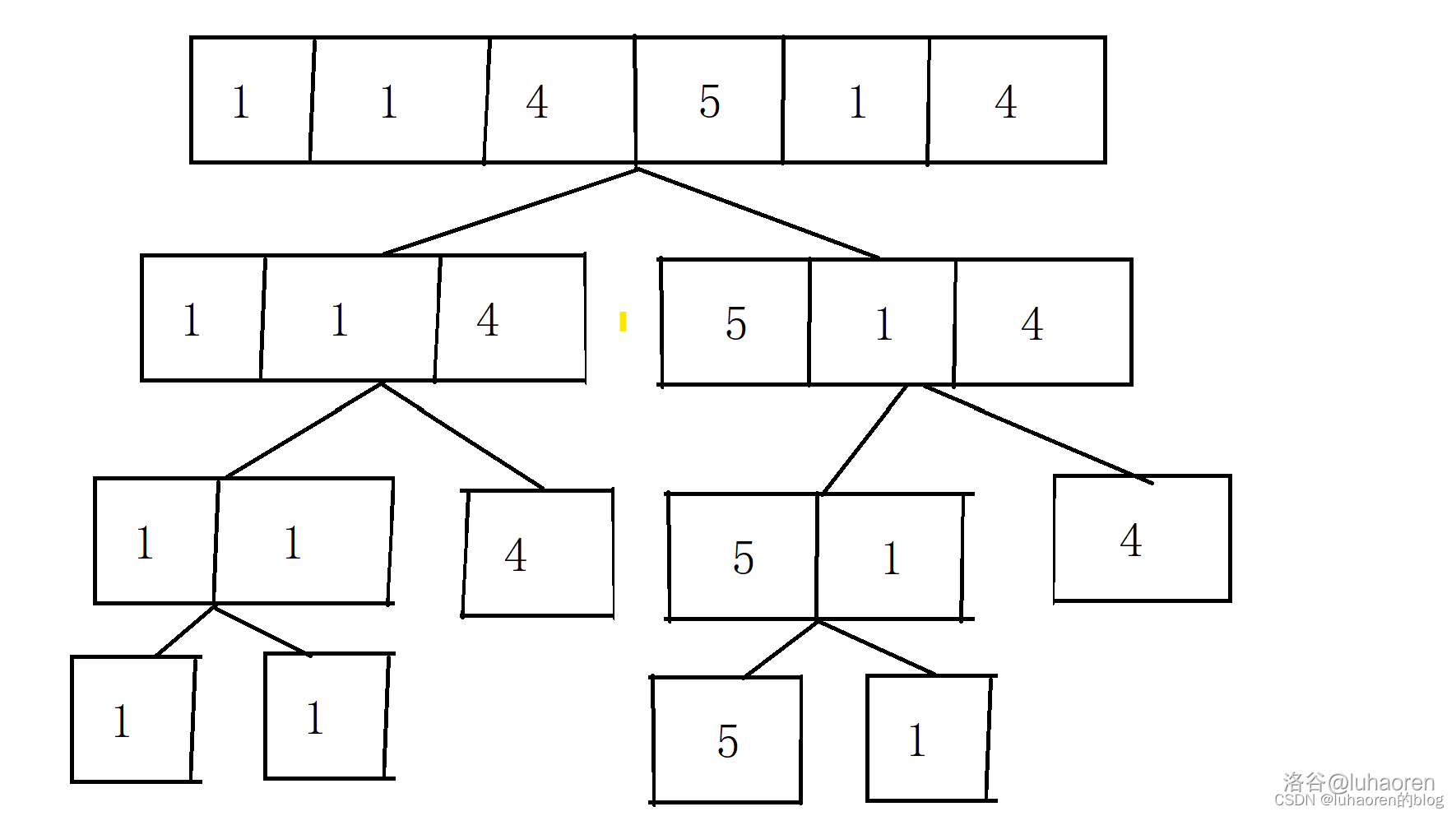
然後我們就可以在每個節點處維護一些資訊。

注意：實際上，只有最下面一層的葉子節點才儲存了實際的數位，其它的每個節點只儲存著這個區間的資訊（如區間和，區間最值等）

那麼如何把子節點的資訊傳到父節點上呢？

我們要了解一個叫做\(pushup\)的操作。

void pushup(int x){
	tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;
}

這個操作的意思就是：節點表示的區間和等於兩個子節點所表示的區間之和。即下圖：

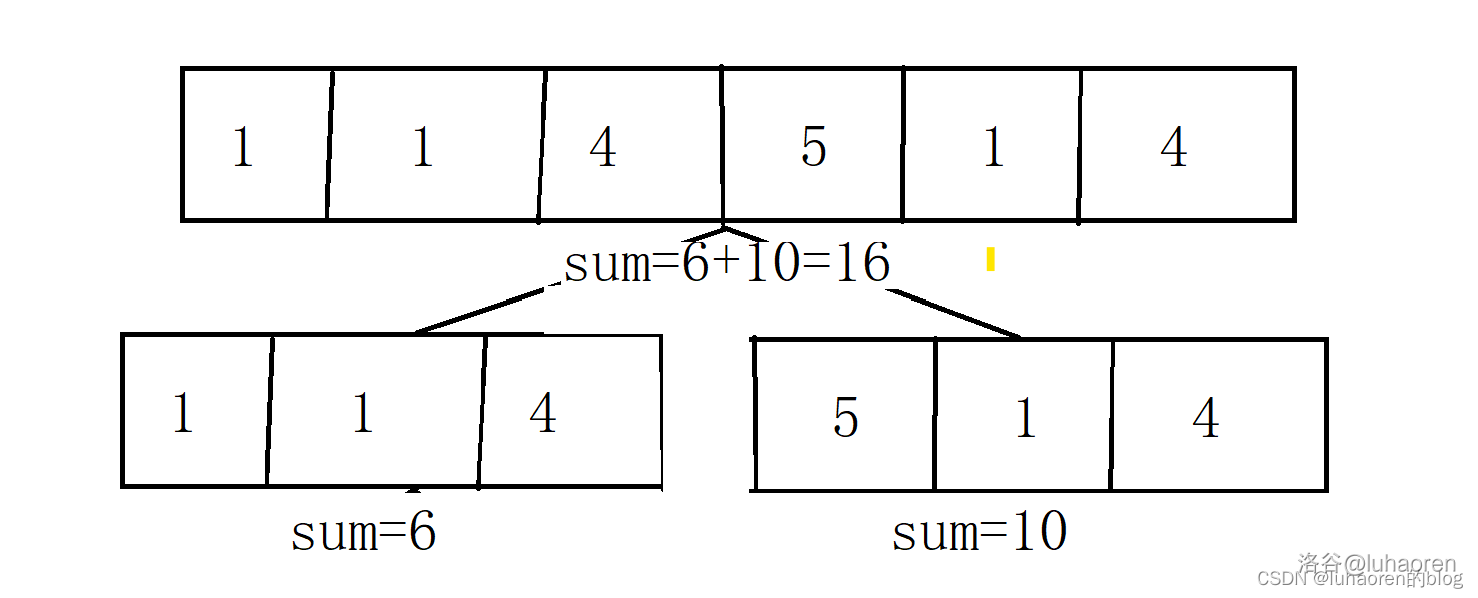
有了這個操作，我們就可以遞迴的求出每一個節點所表示的資訊。

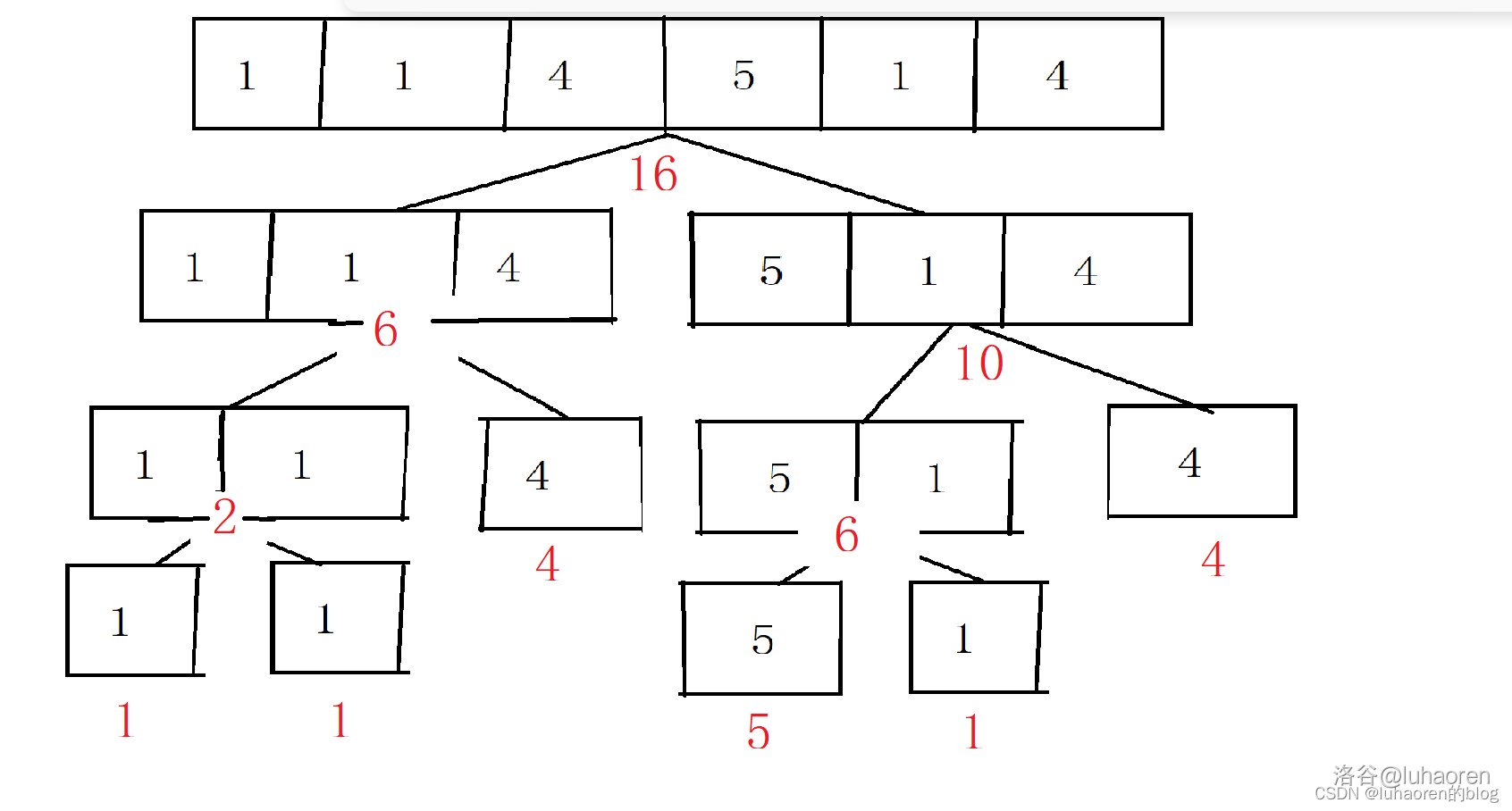
這個建立線段樹的過程可以看作是預處理資訊，把陣列的資訊轉移到線段樹的葉子節點上，時間複雜度大概是\(O(n)\)

事實上，還有另一種寫法的線段樹，不需要建樹，但是需要\(O( n\log n)\)的時間複雜度插入資料，我們會在權值線段樹部分介紹這種寫法。

建樹程式碼

void build(int x,int l,int r){
	tr[x].l=l,tr[x].r=r;//節點表示區間的左右界
	if(l==r){
		//若l=r，說明這個節點是葉子節點，直接賦值
		tr[x].sum=a[l];//a是原數列
		return;
	}
	int mid=(l+r)/2;//mid表示左右子區間的間隔
	build(x*2,l,mid),build(x*2+1,mid+1,r);//遞迴建樹
	//線段樹是完全二元樹，左右子節點可以用x*2,x*2+1表示
	tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;//pushup操作
}

區間查詢

線段樹可以在\(O(\log n)\)的時間複雜度下完成區間查詢操作。

以剛剛的數列\(\left \{ 1,1,4,5,1,4 \right \}\)為例。

此時如果詢問\([3,5]\)之間的區間和，我們該怎麼辦呢？

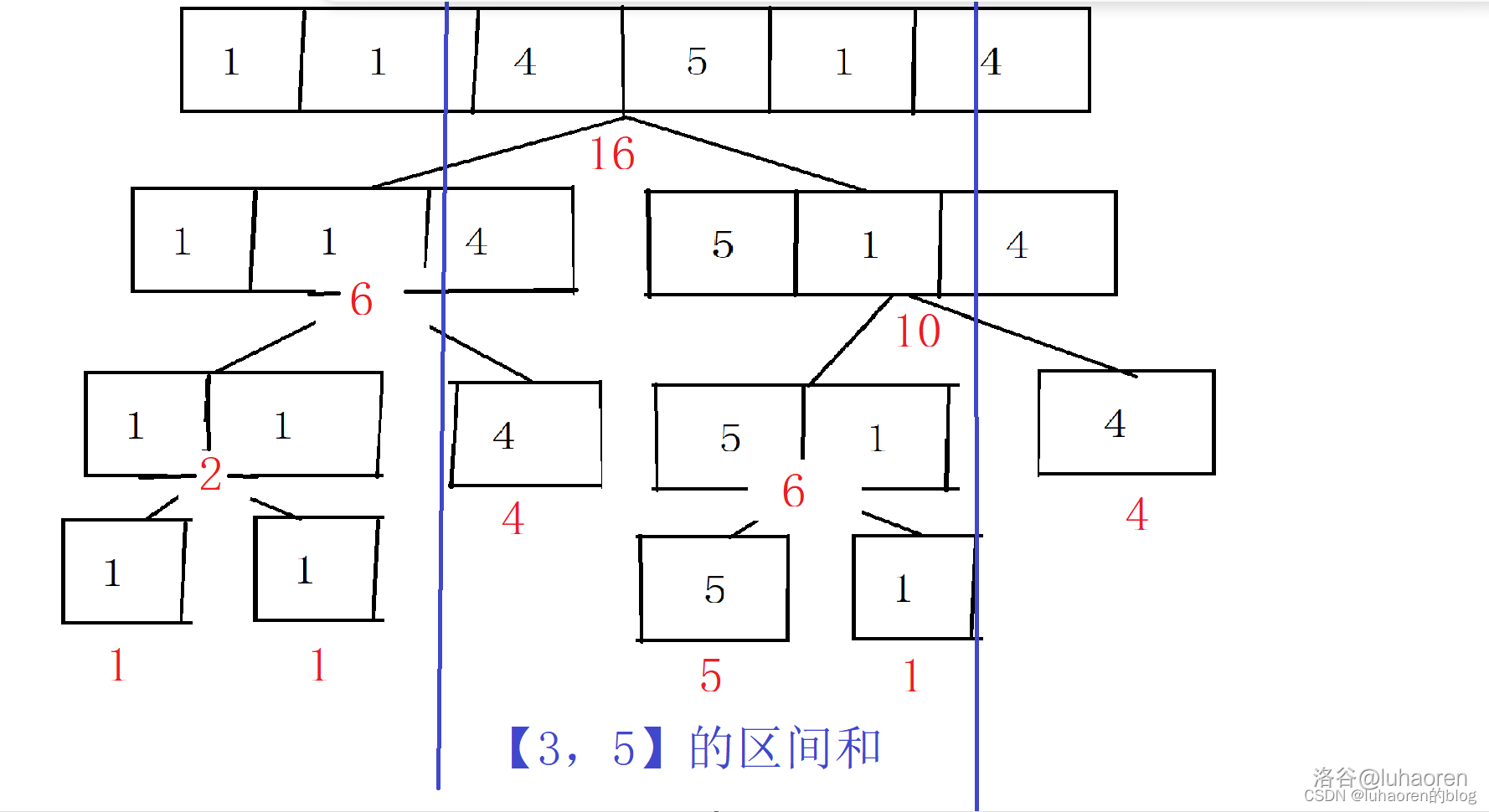
首先，如果直接查詢\([4,6]\)的區間和，我們肯定是會的，直接輸出10就行。

查詢\([4,5]\)怎麼辦呢？

可以把\([4,6]\)拆成\([4,5]\)和\([6,6]\)，然後輸出\([4,5]\)的和。

那麼\([3,5]\)就可以表示為\([3,3]\)和\([4,5]\)。

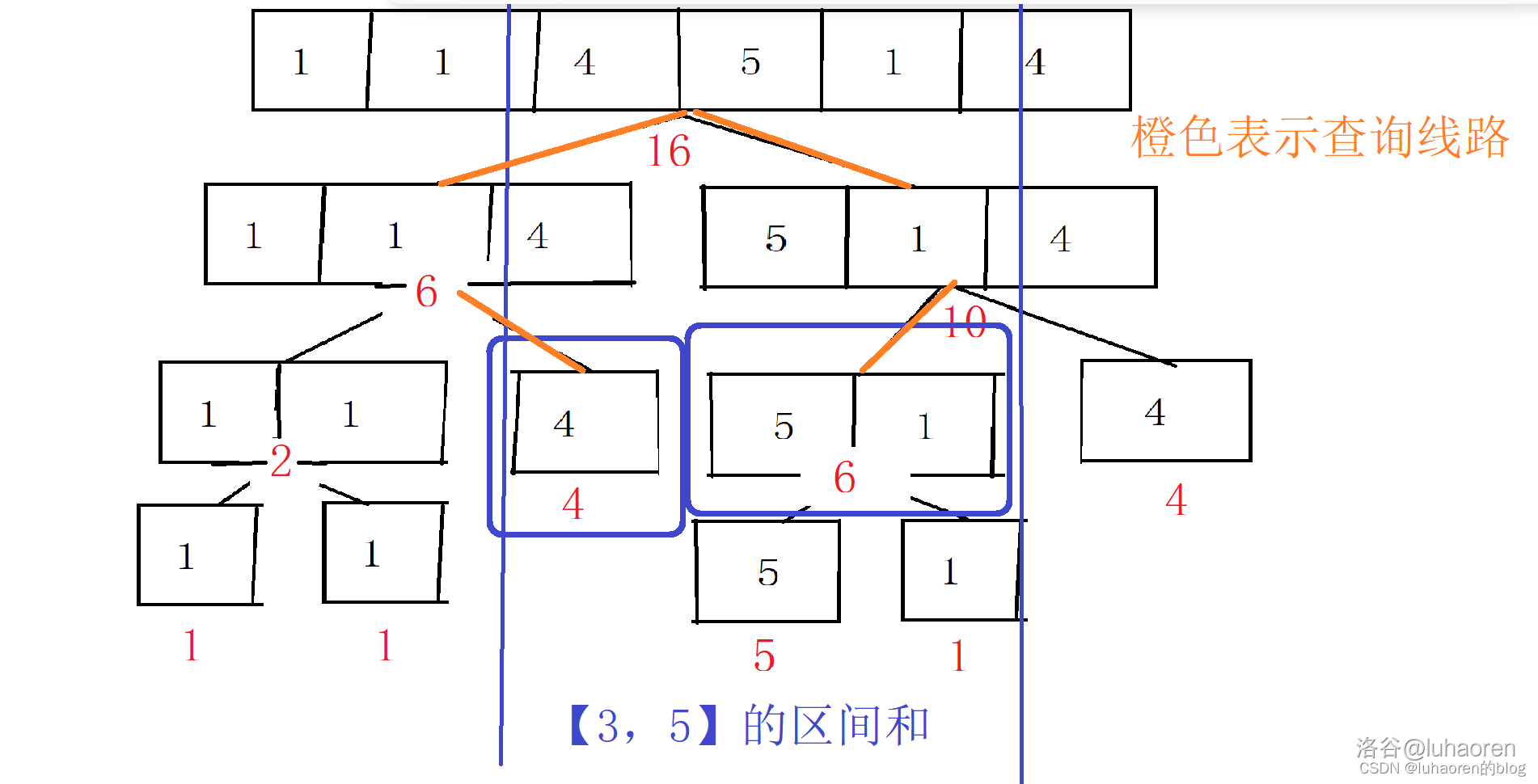
所以無論我們查詢多大的區間，都可以拆成一些（不超過\(\log n\)）預處理過的子區間，把這些子區間的區間和加起來，就是答案。

區間查詢程式碼

int query(int x,int l,int r){
	//區間查詢
	if(tr[x].l>=l&&tr[x].r<=r) return tr[x].sum;//如果該節點的區間被要查詢的區間包括了，那麼就不用繼續找了，直接返回改節點的值就行了
	int mid=(tr[x].l+tr[x].r)/2;
	int sum=0;
	if(l<=mid) sum+=query(x*2,l,r);//如果當前節點在要查詢區間左邊界的右面，那麼遞迴查詢左子樹
	if(r>mid) sum+=query(x*2+1,l,r);//如果當前節點在要查詢區間右邊界的左面，那麼遞迴查詢右子樹
	return sum;//由此得出了該區間的值，返回即可
}

單點修改

單點修改比較簡單，不斷遞迴，定位到要找的節點，修改即可。

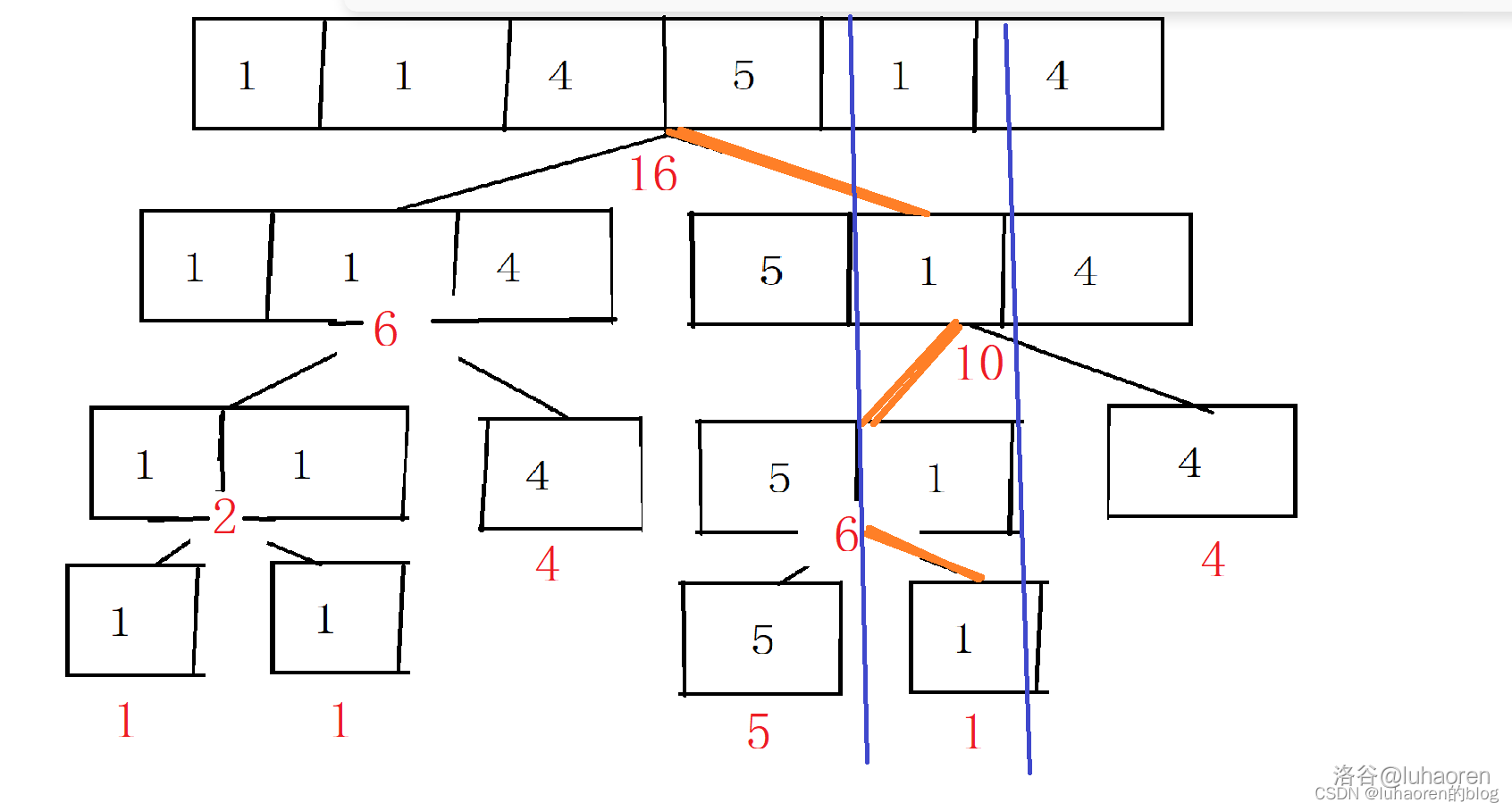
單點修改程式碼

void change(int now,int x,int k){
	//單點修改
	if(tr[now].l==tr[now].r){
		tr[now].sum=k;//如果找到了該節點，那麼修改它
		return;
	}
	int mid=(tr[now].l+tr[now].r)/2;
	if(x<=mid) change(now*2,x,k);//如果要尋找的節點在當前節點的左側，就遞迴左子樹
	else change(now*2+1,x,k);//否則遞迴右子樹
	tr[now].sum=tr[now*2].sum+tr[now*2+1].sum;//pushup操作，維護每個節點的sum值
}

線段樹的儲存

觀察線段樹，我們發現它是一個完全二元樹，可以用堆式儲存法。

即把每個節點都存在一個陣列裡，因為是完全二元樹，所以兩個子節點可以用\(2p\)，\(2p+1\)表示。

因為線段樹大部分節點都不是用來存數位的，所以線段樹所用的空間要比原數列的空間多很多，如圖，只有紅色的節點才是真正存數位的。

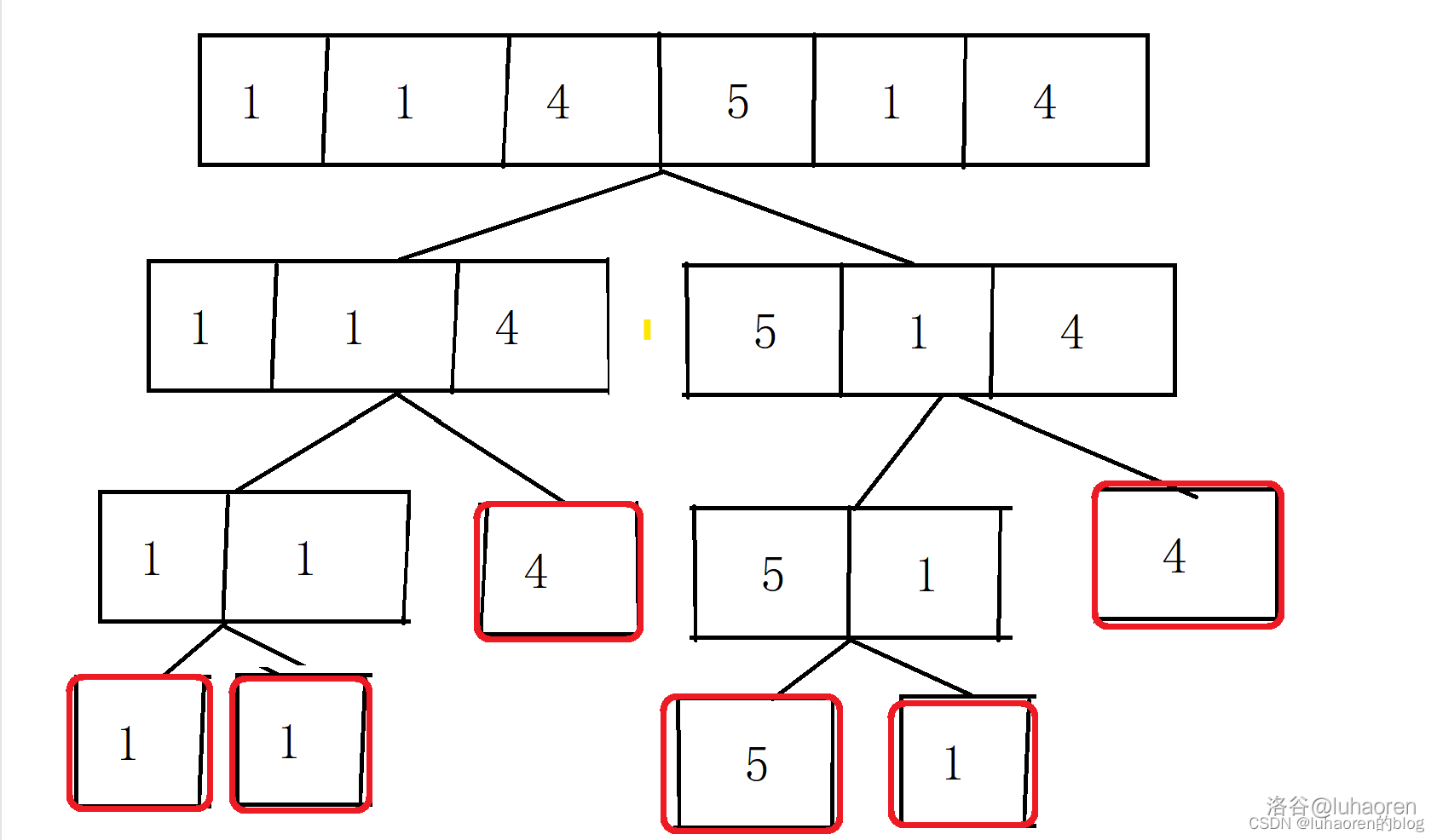
線段樹大概要開四倍的空間，具體可以看OIwiki上的分析。

例題1：單點修改，區間查詢

洛谷P3374

已知一個數列，進行下面兩種操作：

• 將某一個數加上\(x\)
• 求出某區間每一個數的和

題目分析

相當於模板題，可以嘗試著敲一遍，這裡提供程式碼。

AC程式碼

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct node{
	int sum,l,r;//線段樹節點的結構體
}tr[N*4];//線段樹需要開四倍空間
int a[N];
inline void pushup(int x){
	tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;
}
void build(int x,int l,int r){
	tr[x].l=l,tr[x].r=r;//節點表示區間的左右界
	if(l==r){
		//若l=r，說明這個節點是葉子節點，直接賦值
		tr[x].sum=a[l];//a是原數列
		return;
	}
	int mid=(l+r)/2;//mid表示左右子區間的間隔
	build(x*2,l,mid),build(x*2+1,mid+1,r);//遞迴建樹
	//線段樹是完全二元樹，左右子節點可以用x*2,x*2+1表示
	pushup(x);//pushup操作
}
int query(int x,int l,int r){
	//區間查詢
	if(tr[x].l>=l&&tr[x].r<=r) return tr[x].sum;//如果該節點的區間被要查詢的區間包括了，那麼就不用繼續找了，直接返回改節點的值就行了
	int mid=(tr[x].l+tr[x].r)/2;
	int sum=0;
	if(l<=mid) sum+=query(x*2,l,r);//如果當前節點在要查詢區間左邊界的右面，那麼遞迴查詢左子樹
	if(r>mid) sum+=query(x*2+1,l,r);//如果當前節點在要查詢區間右邊界的左面，那麼遞迴查詢右子樹
	return sum;//由此得出了該區間的值，返回即可
}
void change(int now,int x,int k){
	//單點修改
	if(tr[now].l==tr[now].r){
		tr[now].sum+=k;//如果找到了該節點，那麼修改它
		return;
	}
	int mid=(tr[now].l+tr[now].r)/2;
	if(x<=mid) change(now*2,x,k);//如果要尋找的節點在當前節點的左側，就遞迴左子樹
	else change(now*2+1,x,k);//否則遞迴右子樹
	pushup(now);//pushup操作，維護每個節點的sum值
}

int n,q;
int main(){
	cin>>n>>q;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(1,1,n);//建樹
	while(q--){
		int t,b,c;
		cin>>t>>b>>c;
		if(t==1) change(1,b,c);
		else cout<<query(1,b,c)<<endl;
	}
}

習題

學會了線段樹最基礎的部分，就可以做一些習題了，將在部落格的最後提供題解和程式碼。

1. JSOI2008 最大數
   線段樹維護最大值的模板
2. loj10123. Balanced Lineup
   RMQ問題，可以試試用線段樹做

懶標記

下面請思考，怎麼才能做到線段樹的區間修改呢？

如果直接把區間遍歷一遍，依次修改，複雜度會達到無法接受的\(O(n\log n)\)。

那麼怎麼能讓區間修改的複雜度變小呢？

我們需要引入一個叫做「懶標記」的東西。

懶標記也叫延遲標記，顧名思義，我們再修改這個區間的時候給這個區間打上一個標記，這樣就可以做到區間修改的\(O(\log n)\)的時間複雜度。

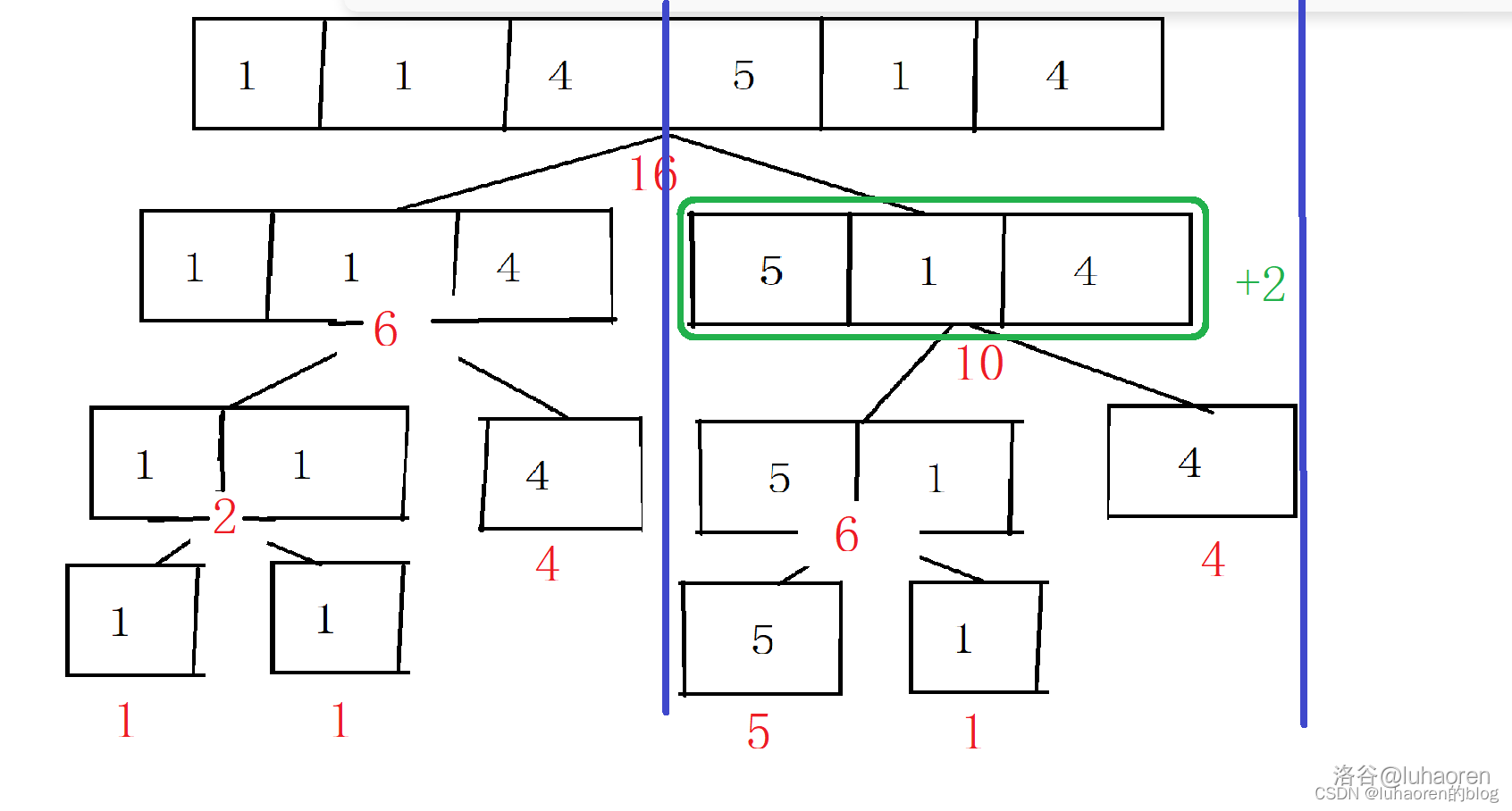
如圖，如果要給\([4,6]\)每個數都加上\(2\)，那麼直接再代表著\([4,6]\)區間的結點打上\(+2\)的標記就行了。

pushdown操作

再想一個問題，在給\([4,6]\)區間打上懶標記後，我們如何查詢\([4,5]\)的值？

如果我們直接查詢到\([4,5]\)區間上，會發現根本就沒有被加上過2。

為什麼呢?

因為現在懶標記打在了\([4,6]\)區間上。而他的子節點壓根沒被修改過！

所以我們需要把懶標記向下傳遞。

這就有了一個操作，叫做pushdown，它可以把懶標記下傳。

設想一下，如果我們要把懶標記下傳，應該注意什麼呢？

首先，要給子節點打上懶標記。

然後，我們要修改子節點上的值。

最後，不要忘記把這個節點的懶標記清空。

pushdown程式碼

inline void pushudown(int x){
	if(tr[x].add){
		//如果這個節點上有懶標記
		tr[2*x].add+=tr[x].add,tr[2*x+1].add+=tr[x].add;
		//把這個節點的懶標記給他的兩個子節點
		tr[2*x].sum+=tr[x].add*(tr[2*x].r-tr[2*x].l+1);
		tr[2*x+1].sum+=tr[x].add*(tr[2*x+1].r-tr[2*x+1].l+1);
		//分別給它的兩個子節點修改
		tr[x].add=0;
		//別忘了清空這個節點的懶標記
	}
}

區間修改

學會了懶標記，應該可以很輕鬆地寫出區間修改的程式碼了。

區間修改的操作很像區間查詢，也是查詢能夠覆蓋住的子區間，然後給它打上懶標記。

區間查詢程式碼

void update(int now,int l,int r,int k){
	if(l<=tr[now].l&&r>=tr[now].r){
		//如果查到子區間了
		tr[now].sum+=k*(tr[now].r-tr[now].l+1);//先修改這個區間
		tr[now].add+=k;//然後給它打上懶標記
		//注：這裡一定要分清順序，先修改，再標記！
	}
	else{
		//如果需要繼續向下查詢
		pushudown(now);//一定要先把懶標記向下傳
		int mid=(tr[now].l+tr[now].r)/2;
		//這裡很像區間查詢
		if(l<=mid) update(now*2,l,r,k);
		if(r>mid) update(now*2+1,l,r,k);	
		//最後別忘了pushup一下
		pushup(now);
	}
}

例題2：區間修改，區間查詢

洛谷P3372

已知一個數列，你需要進行下面兩種操作：

1. 將某區間每一個數加上\(k\)。
2. 求出某區間每一個數的和。

題目分析

應用到區間修改，需要注意的一點是，在區間查詢時，也需要下傳懶標記，這樣才能查詢到真實的值。

AC程式碼

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
	int sum;
	int l,r;
	int add;//懶標記
}tr[N*4];//線段樹要開四倍空間哦
int a[N];//原數列
inline void pushup(int x){
	tr[x].sum=tr[2*x].sum+tr[2*x+1].sum;//pushup操作
}
inline void pushudown(int x){
	if(tr[x].add){
		//如果這個節點上有懶標記
		tr[2*x].add+=tr[x].add,tr[2*x+1].add+=tr[x].add;
		//把這個節點的懶標記給他的兩個子節點
		tr[2*x].sum+=tr[x].add*(tr[2*x].r-tr[2*x].l+1);
		tr[2*x+1].sum+=tr[x].add*(tr[2*x+1].r-tr[2*x+1].l+1);
		//分別給它的兩個子節點修改
		tr[x].add=0;
		//別忘了清空這個節點的懶標記
	}
}
void build(int x,int l,int r){
	//建樹操作
	tr[x].l=l,tr[x].r=r,tr[x].add=0;
	if(l==r){
		tr[x].sum=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(2*x,l,mid),build(2*x+1,mid+1,r);
	pushup(x);
}
int query(int x,int l,int r){
	if(l<=tr[x].l&&r>=tr[x].r) return tr[x].sum;
	pushudown(x);//注意，區間查詢時也要下懶傳標記
	int mid=(tr[x].l+tr[x].r)/2,sum=0;
	if(l<=mid) sum+=query(x*2,l,r);
	if(r>mid) sum+=query(x*2+1,l,r);
	return sum;	
}
void update(int now,int l,int r,int k){
	if(l<=tr[now].l&&r>=tr[now].r){
		//如果查到子區間了
		tr[now].sum+=k*(tr[now].r-tr[now].l+1);//先修改這個區間
		tr[now].add+=k;//然後給它打上懶標記
		//注：這裡一定要分清順序，先修改，再標記！
	}
	else{
		//如果需要繼續向下查詢
		pushudown(now);//先把懶標記向下傳
		int mid=(tr[now].l+tr[now].r)/2;
		//這裡很像區間查詢
		if(l<=mid) update(now*2,l,r,k);
		if(r>mid) update(now*2+1,l,r,k);
		pushup(now);//最後別忘了pushup一下
	}
}
int n,q;
int main(){
	cin>>n>>q;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(1,1,n);
	while(q--){
		int l,r,k,c;
		cin>>c>>l>>r;
		if(c==1){
			cin>>k;
			update(1,l,r,k);
		}
		else cout<<query(1,l,r)<<endl;
	}
	return 0;
}
//別忘了開long long哦

例題3：較複雜的區間操作

洛谷P3373

已知一個數列，你需要進行下面三種操作：

1. 將某區間每一個數乘上\(x\)。

2. 將某區間每一個數加上\(x\)。

3. 求出某區間每一個數的和。

題目分析

有些題要維護多個區間操作，這在pushdown操作上就比較麻煩，比如這道題，要求維護區間加法和區間乘法，所以我們得維護兩個懶標記。

那麼我們該怎樣安排懶標記的pushdown順序呢？

我們考慮先乘後加的維護順序，假設兩個懶標記分別是\(mul\)和\(add\)，那麼這個數值就應該是\(mul \times sum+add\)。

此時如果加上一個\(add\)，就會變成 \(mul \times sum+add+add\)

如果乘上一個\(mul\)那就是\(mul \times sum \times mul+add \times mul\)

這種方式便於計算，如果使用先加後乘的方式，就會比較麻煩甚至會出錯。

AC程式碼

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
	int l,r;
	int sum,add,mul;
}tr[N*4];//線段樹開四倍空間
int a[N];
int n,p,m;
inline void pushup(int x){
	tr[x].sum=(tr[2*x].sum+tr[2*x+1].sum)%p;
}
inline void eval(int x,int add,int mul){
	//我們把計算懶標記單獨放在這個函數裡，否則好多東西擠一塊很難看
	tr[x].sum=(tr[x].sum*mul+add*(tr[x].r-tr[x].l+1))%p;
	tr[x].mul=(mul*tr[x].mul)%p; 	//先計算乘法懶標記
	tr[x].add=(tr[x].add*mul+add)%p;//再算加法懶標記
}

inline void pushdown(int x){
	//依次計算兩個子節點的值和懶標記
	eval(x*2,tr[x].add,tr[x].mul);
	eval(x*2+1,tr[x].add,tr[x].mul);
	tr[x].add=0,tr[x].mul=1;
	//清空懶標記，注意：乘法懶標記要初始化成1
}
void build(int x,int l,int r){
	tr[x].l=l,tr[x].r=r;
	tr[x].add=0,tr[x].mul=1;//乘法懶標記要初始化成1
	if(l==r){
		tr[x].sum=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(x*2,l,mid),build(x*2+1,mid+1,r);//遞迴建樹
	pushup(x);
}
void change(int x,int l,int r,int add,int mul){
	if(l<=tr[x].l&&r>=tr[x].r) eval(x,add,mul);//計算
	else{
		pushdown(x);
		int mid=(tr[x].l+tr[x].r)/2;
		if(l<=mid) change(x*2,l,r,add,mul);
		if(r>mid) change(x*2+1,l,r,add,mul);
		pushup(x);
	}
}
int query(int x,int l,int r){
	if(l<=tr[x].l&&r>=tr[x].r) return tr[x].sum;
	int sum=0;
	pushdown(x); //區間查詢時也要pushdown  
	int mid=(tr[x].l+tr[x].r)/2;
	if(l<=mid) sum+=query(x*2,l,r)%p;
	if(r>mid) sum+=query(x*2+1,l,r)%p;
	return sum;
}
int main(){
	int t,g,c,ch;
	cin>>n>>m>>p;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(1,1,n);
	while(m--){
		cin>>ch>>t>>g;
		if(ch==1){
			cin>>c;
			change(1,t,g,0,c);          
		}
		else if(ch==2){
			cin>>c;
			change(1,t,g,c,1);          
		}
		else cout<<query(1,t,g)%p<<endl;
	}
	return 0;
}
//記得開longlong

標記永久化

其實，維護區間修改的方式有兩種，一種是懶標記和標記下傳，另一種叫做」標記永久化「。

標記永久化，就是不下傳標記，在每次查詢時把經過的標記累加起來，查詢時加起來。

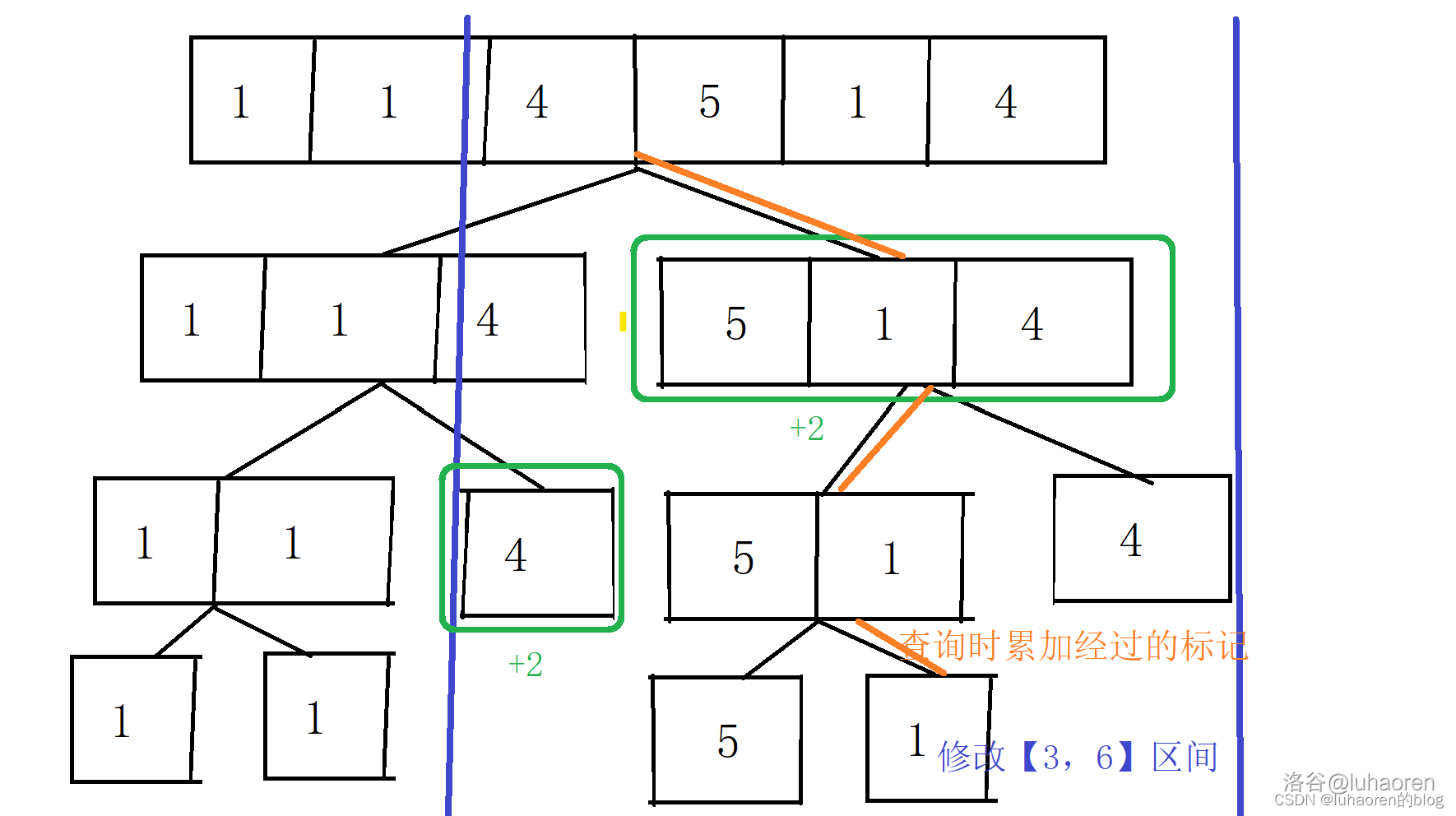
如圖，打上標記的節點用綠色表示，查詢路線（橙色）經過的就累加。

標記永久化程式碼

const int N=1e4+10;
struct node{
	int sum,add;
	int l,r;
}tr[N*4];
int a[N];
void build(int x,int l,int r){
	tr[x].l=l,tr[x].r=r;
	if(l==r){
		tr[x].sum=a[l],tr[x].add=0;
		return;
	}
	int mid=(l+r)/2;
	build(x*2,l,mid),build(x*2+1,mid+1,r);
	tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;//標記永久化中只有建樹時需要用到pushup操作
}
void update(int x,int l,int r,int k){
	tr[x].sum+=(min(tr[x].r,r)-max(tr[x].l,l)+1)*k;//要取一個交集來加
	if(tr[x].l>=l&&tr[x].r<=r){
		tr[x].add+=k;//給節點打上標記後不用下傳。
		return;
	}
	int mid=(tr[x].l+tr[x].r)/2;
	if(l<=mid) update(x*2,l,r,k);
	if(r>mid) update(x*2+1,l,r,k);
}
int query(int x,int l,int r,int add){
	if(tr[x].l>=l&&tr[x].r<=r){
		int s=(tr[x].r-tr[x].l+1)*add;//查詢到節點後給這個區間乘上add
		return tr[x].sum+s;
	}
	add+=tr[x].add;//add代表查詢經過的懶標記之和	
	int mid=(tr[x].l+tr[x].r)/2,sum=0;
	if(l<=mid) sum+=query(x*2,l,r,add);
	if(r>mid) sum+=query(x*2+1,l,r,add);
	return sum;
}

標記永久化應用很多，比如可持久化線段樹中的區間修改，樹套樹中第二維的修改。（後面都將講到）

習題

這裡給出一些習題，按照難度排序。

1. AHOI2009 維護序列
   與例題3差不多
2. 洛谷P1253 扶蘇的問題
   稍微複雜的懶標記維護
3. 洛谷P5142 區間方差
   需要一定的數學推導能力
4. P4145 花神遊歷各國
   想一想如何優化？
5. P1471 方差
   3題的加強版，較難
6. P6327 區間加區間sin和
   需要一些高中的數學知識

權值線段樹

權值線段樹是線段樹的一種衍生演演算法，其基本儲存結構和線段樹基本相同。

權值線段樹與線段樹的不同點在於，線段樹維護區間資訊，權值線段樹維護值域資訊。

如圖，權值線段樹就長這個樣子。

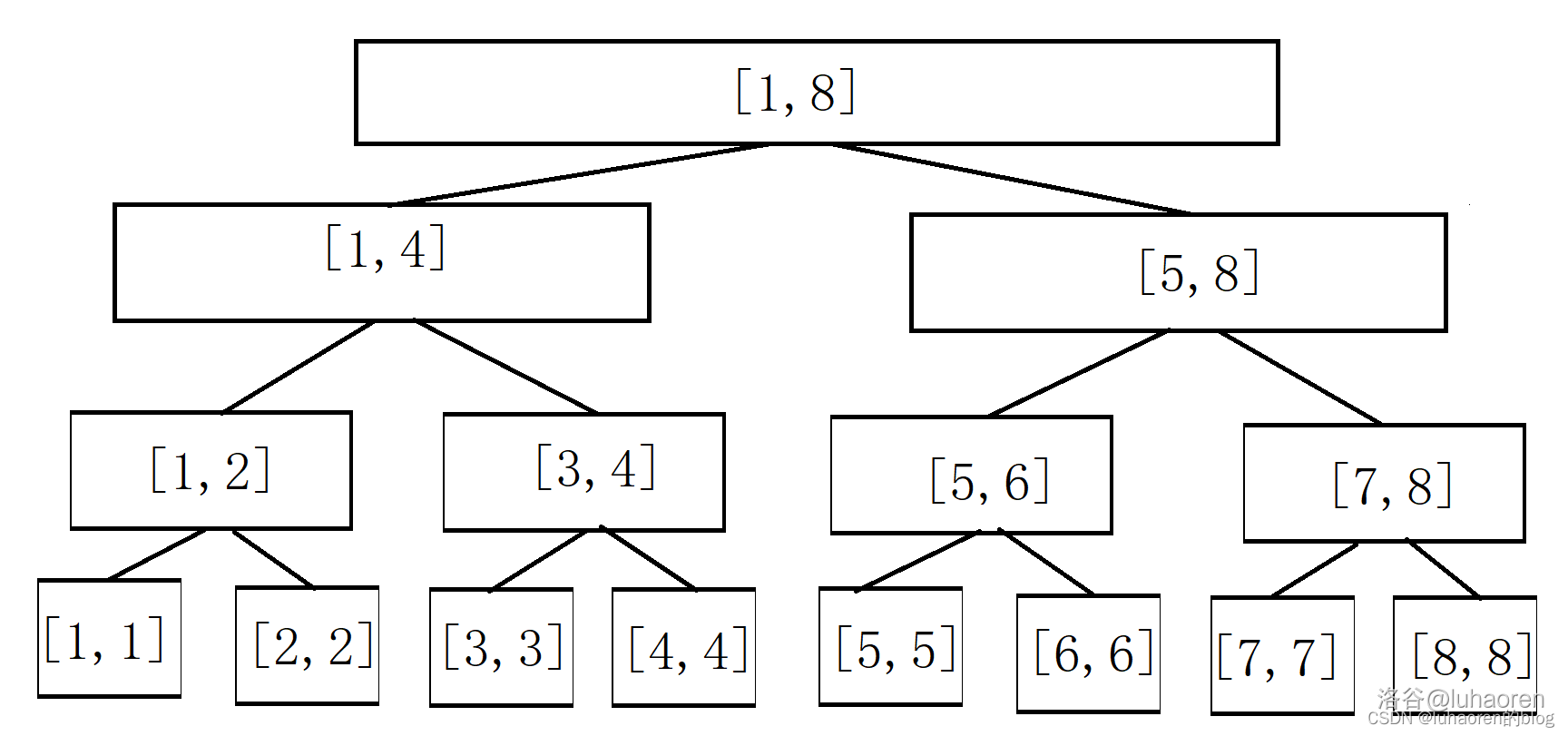
看起來和線段樹沒什麼區別吧，現在我們插入一個數\(4\)。

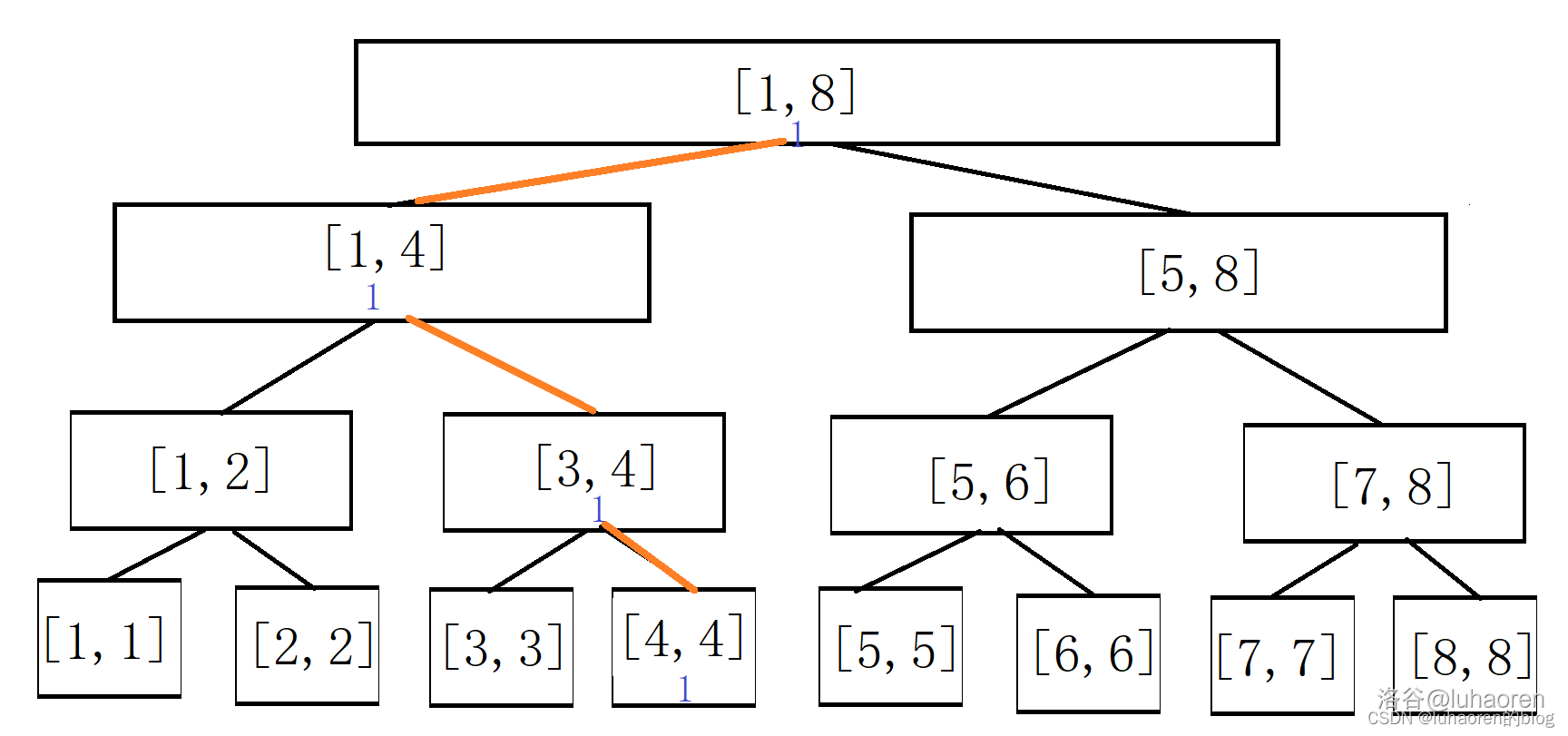
每一個包含\(4\)的區間都被加上了1。

那麼每個區間維護的到底是什麼呢？

是這個區間內的數的數量。

當我們依次插入\(\{4,1,7,2,8 \}\)後，這個權值線段樹就變成了這樣。

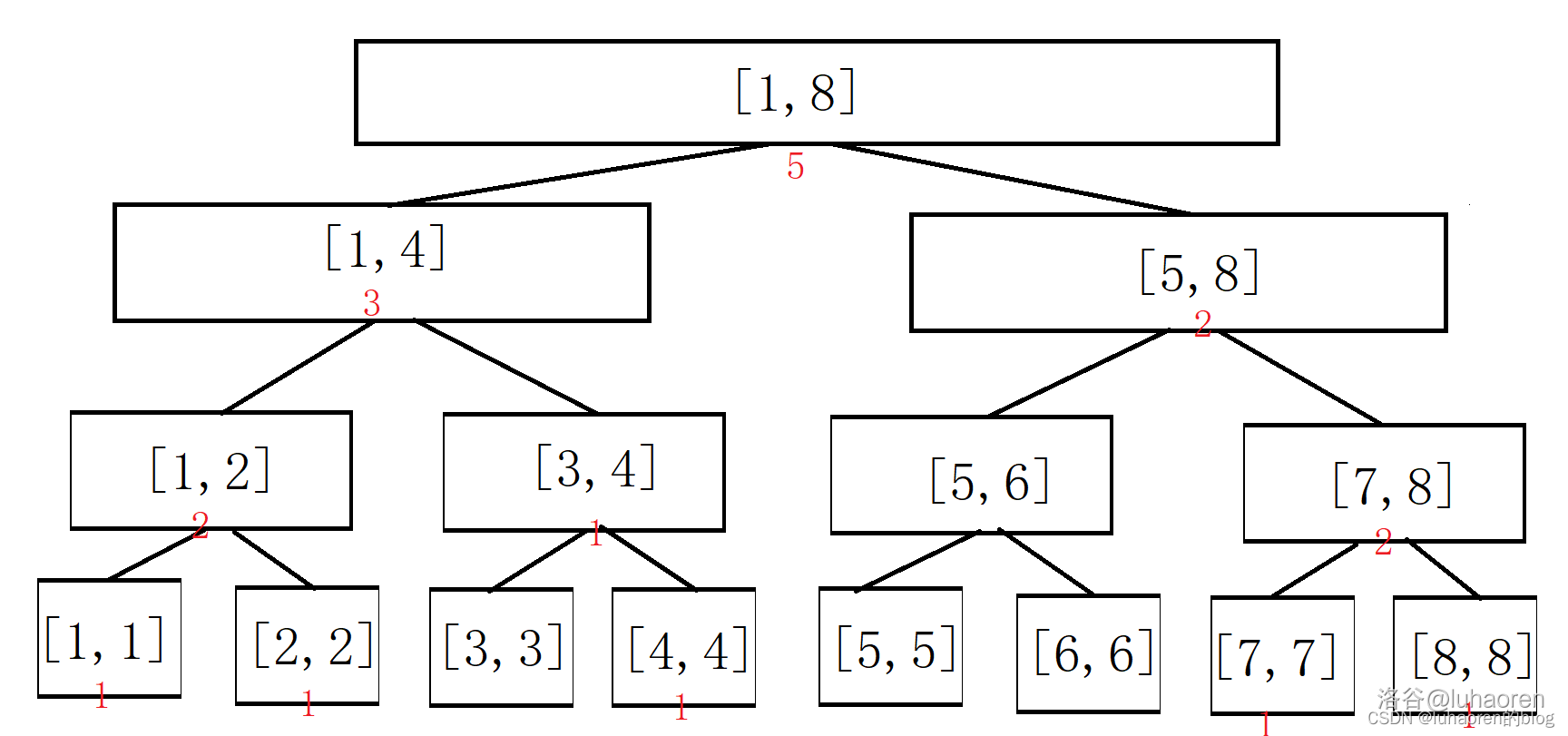
這就是權值線段樹的原理。

權值線段樹可以幹很多事情，比如查詢第\(k\)小，查詢前驅後繼等。

插入與刪除

想一想，我們該如何實現插入一個數的操作呢？

把從這個數的節點到根節點的路徑上每一個節點都加上1即可。

刪除呢？

減去1就行了。

程式碼模板

int tr[N*4];
//這就是上文提到過的線段樹的另一種寫法，因為權值線段樹不需要維護區間資訊，所以不需要建樹的預處理，這種寫法就變得很方便。
inline void pushup(int x){
	tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k){
	//插入一個數k
	if(l==r){
		tr[x]++;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(x*2,l,mid,k);
	else insert(x*2+1,mid+1,r,k);
	pushup(x);
}
void del(int x,int l,int r,int k){
	//刪除一個數k
	if(l==r){
		tr[x]--;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) del(x*2,l,mid,k);
	else del(x*2+1,mid+1,r,k);
	pushup(x);
}
int query(int x,int l,int r,int ql,int qr){
	//查詢ql，qr之間一共有多少個數
	if(l>=ql&&r<=qr) return tr[x];
	int mid=(l+r)/2,sum=0;
	if(ql<=mid) sum=query(x*2,l,mid,ql,qr);
	if(qr>mid) sum+=query(x*2+1,mid+1,r,ql,qr);
	return sum;
}

例題4：權值線段樹

loj 10116

NK 中學組織同學們去五雲山寨參加社會實踐活動，按慣例要乘坐火車去。由於 NK 中學的學生很多，在火車開之前必須清點好人數。

初始時，火車上沒有學生。當同學們開始上火車時，年級主任從第一節車廂出發走到最後一節車廂，每節車廂隨時都有可能有同學上下。年級主任走到第\(m\)節車廂時，他想知道前\(m\)節車廂上一共有多少學生。每次提問，m 總會比前一次大。

題目分析

很明顯可以用權值線段樹做，維護每個區間的數的數量，具體見程式碼。

AC程式碼

#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int tr[N*4];//權值線段樹維護的是值域，所以要開n的範圍的四倍
inline void pushup(int x){
	tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k,int p){
	if(l==r){
		tr[x]+=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(x*2,l,mid,k,p);
	else insert(x*2+1,mid+1,r,k,p);
	pushup(x);
}
int query(int x,int l,int r,int ql,int qr){
	if(l>=ql&&r<=qr) return tr[x];
	int mid=(l+r)/2,sum=0;
	if(ql<=mid) sum=query(x*2,l,mid,ql,qr);
	if(qr>mid) sum+=query(x*2+1,mid+1,r,ql,qr);
	return sum;
}
int n,k;
int main(){
	cin>>n>>k;
	while(k--){
		char opt;
		int m,p;
		cin>>opt;
		if(opt=='A'){
			cin>>m;
			cout<<query(1,1,n,1,m)<<endl;
		}
		else if(opt=='B'){
			//上車
			cin>>m>>p;
			insert(1,1,n,m,p);
		}
		else{
			//下車
			cin>>m>>p;
			insert(1,1,n,m,-p);
		}
	}
}

查詢第k大數

請注意，這個查詢第k大是針對整個權值線段樹的，要查區間第k大請去學主席樹或樹套樹。

權值線段樹是維護值域的，一個節點的左右端點都應該是一個具體的數位，而且值域肯定是遞增的，所以我們可以二分。

如果 \(k\)小於區間中點，那麼也就說明結果為左區間第\(k\)大數。否則，也就說明結果為右區間第\(k−l_{size}\)大數。

程式碼

int kth(int x,int l,int r,int k){
	if(l==r) return l;//查到了，返回即可
	int mid=(l+r)/2;
	if(k<=tr[x*2]) return kth(x*2,l,mid,k); 
	return kth(x*2+1,mid+1,r,k-tr[x*2]);
}

查詢一個數的排名

和查詢第k大差不多。

每次把\(x\)與當前區間中點\(mid\)比較，如果小於等於\(mid\)，說明在左區間，向左兒子尋找。
如果大於\(mid\)，說明在右區間，這時，它的排名要加上左子樹的大小（它比整個左子樹的數都大）

如果找到葉子節點了，那麼返回\(1\)(在\([l,r]\)的區間只有自己，排名第一)

程式碼

int rnk(int x,int l,int r,int k){
	if(l==r) return 1;
	int mid=(l+r)/2;
	if(k<=mid) return rnk(x*2,l,mid,k);
	return rnk(x*2+1,mid+1,r,k)+tr[x*2];
}

例題5：用權值線段樹實現平衡樹

洛谷P3369

實現一個資料結構，來維護一些數，其中需要提供以下操作：

1. 插入\(x\)數
2. 刪除\(x\)數(若有多個相同的數，應只刪除一個)
3. 查詢\(x\)數的排名(排名定義為比當前數小的數的個數\(+1\))
4. 查詢排名為\(x\)的數
5. 求\(x\)的前驅(前驅定義為小於\(x\)，且最大的數)
6. 求\(x\)的後繼(後繼定義為大於\(x\)，且最小的數)

題目分析

正宗解法自然是平衡樹，但是仔細觀察這些操作，似乎都可以用權值線段樹解決？

前四個操作我們已經講解過了，只剩下最後兩個：求前驅和後繼。

前驅實際上就是比\(x\)的排名小一位的數，也就是kth(rnk(x)-1)。

後繼就是\(x+1\)的排名位置的數，也就是kth(rnk(x+1))。

那麼我們就可以寫出程式碼了？

沒AC程式碼

#include <bits/stdc++.h>
using namespace std;
const int N=1e7+10;
int tr[8*N];//因為要維護正負區間，所以開二倍，再加線段樹的四倍空間，就是八倍
inline void pushup(int x){
	tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k,int p){
	//若p為1則插入，若p為-1則刪除
	if(l==r){
		tr[x]+=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(x*2,l,mid,k,p);
	else insert(x*2+1,mid+1,r,k,p);
	pushup(x);
}
int kth(int x,int l,int r,int k){
	//查詢排名為k的數
	if(l==r) return l;
	int mid=(l+r)/2;
	if(k<=tr[x*2]) return kth(x*2,l,mid,k); 
	return kth(x*2+1,mid+1,r,k-tr[x*2]);
}
int rnk(int x,int l,int r,int k){
	//查詢數k的排名
	if(l==r) return 1;
	int mid=(l+r)/2;
	if(k<=mid) return rnk(x*2,l,mid,k);
	return rnk(x*2+1,mid+1,r,k)+tr[x*2];
}
int n;
int main(){
	cin>>n;
	while(n--){
		int opt,x;
		cin>>opt>>x;
		switch(opt){
		case 1:
			insert(1,-N,N,x,1);//插入
			break;
		case 2:
			insert(1,-N,N,x,-1);//刪除
			break;
		case 3:
			cout<<rnk(1,-N,N,x)<<endl;
			break;
		case 4:
			cout<<kth(1,-N,N,x)<<endl;
			break;
		case 5:
			cout<<kth(1,-N,N,rnk(1,0,N,x)-1)<<endl;
			break;
		case 6:
			cout<<kth(1,-N,N,rnk(1,0,N,x)+1)<<endl;
			break;
		}
	}
}

細心的你會發現，這個線段樹怎麼開了\(8\times10^7\)呢？肯定會爆空間啊。

但是題目要求的\(|x|\le10^7\)卻令我們不得不開這麼大。

怎麼辦呢？

一般來說，優化線段樹空間的有兩種方法。

一種是離散化後再進行操作（離線），一種是動態開點。

（這兩種方法都會在下一節介紹到）

在這道題中，我們可以使用動態開點的方式，優化空間。

‘動態開點程式碼

#include <bits/stdc++.h>
using namespace std;
const int N=1e7+10,M=4e5+10;
int tr[M];
int ls[M],rs[M],tot=0;
inline void pushup(int x){
	tr[x]=tr[ls[x]]+tr[rs[x]];//動態開點後，就不能用x*2的方式存了，得開lsrs兩個陣列（或結構體）
}
void insert(int &x,int l,int r,int k,int p){//x是參照形式，方便傳值
	if(!x) x=++tot;//動態開點
	//若p為1則插入，若p為-1則刪除
	if(l==r){
		tr[x]+=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(ls[x],l,mid,k,p);
	else insert(rs[x],mid+1,r,k,p);
	pushup(x);
}
int kth(int x,int l,int r,int k){
	if(l==r) return l;//查到了，返回即可
	int mid=(l+r)/2;
	if(k<=tr[ls[x]]) return kth(ls[x],l,mid,k); 
	return kth(rs[x],mid+1,r,k-tr[ls[x]]);
}
int rnk(int x,int l,int r,int k){
	if(l==r) return 1;
	int mid=(l+r)/2;
	if(k<=mid) return rnk(ls[x],l,mid,k);
	return rnk(rs[x],mid+1,r,k)+tr[ls[x]];
}
int n,root;
int main(){
	cin>>n;
	while(n--){
		int opt,x;
		cin>>opt>>x;
		switch(opt){
		case 1:
			insert(root,-N,N,x,1);//因為動態開點的插入寫成參照形式，所以需要帶進去一個變數
			break;
		case 2:
			insert(root,-N,N,x,-1);//刪除
			break;
		case 3:
			cout<<rnk(root,-N,N,x)<<endl;
			break;
		case 4:
			cout<<kth(root,-N,N,x)<<endl;
			break;
		case 5:
			cout<<kth(root,-N,N,rnk(root,-N,N,x)-1)<<endl;
			break;
		case 6:
			cout<<kth(root,-N,N,rnk(root,-N,N,x+1))<<endl;
			break;
		}
	}
}

如果想學習離散化的解法，可以看這位%%%的部落格。

空間優化技巧

這裡介紹兩種優化方式：離散化和動態開點。

兩種方法其實各有優劣，如果只是為了縮小值域，離散化似乎更好寫一點，但是動態開點還可以被應用到可持久化、線段樹合併和分裂上，所以都學一學吧。

離散化

資料範圍太大了，需要縮小資料範圍，這句話讓你想到了什麼？

當然是離散化了！

所以我們可以把所有操作都存起來，排序然後離散化，離線進行操作。

如果你不會離散化，請看這篇部落格。

動態開點

動態開點，顧名思義，就是使用的時候再開點。

如果資料範圍是\([-10^7,10^7]\)，在權值線段樹的使用過程中，很大一部分的節點會使用不到，這會造成一種浪費。

動態開點的意思就是：不一上來就把所有的節點全部建立起來，只在需要用到一個節點的時候再建立一個節點。

注意：使用動態開點線段樹的話，節點的下標將是無序的，因此必須建立結構體或用兩個陣列來分別儲存一個節點的左右子節點。

程式碼模板

int tr[M];
int ls[M],rs[M],tot=0;
inline void pushup(int x){
	tr[x]=tr[ls[x]]+tr[rs[x]];//動態開點後，就不能用x*2的方式存了，得開lsrs兩個陣列（或結構體）
}
void insert(int &x,int l,int r,int k){//x是參照形式，方便傳值
	if(!x) x=++tot;//動態開點
	if(l==r){
		tr[x]++;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(ls[x],l,mid,k);
	else insert(rs[x],mid+1,r,k);
	pushup(x);
}

習題

提供幾道權值線段樹的習題。

1. loj10114.數星星 Stars
   權值線段樹，需要用動態開點或離散化的優化
2. P1168 中位數
   離散化，然後開權值線段樹維護
3. P2073 送花
   可以用權值線段樹做
4. SDOI2014 旅行
   樹鏈剖分（如果你會的話），用動態開點維護

zkw線段樹

zkw線段樹是一種用迴圈實現的線段樹，比正常的遞迴式線段樹快很多，而且好寫。

zkw線段樹的引入

我們觀察一個線段樹的結構，按照堆式儲存，葉子節點的序號是連續的。

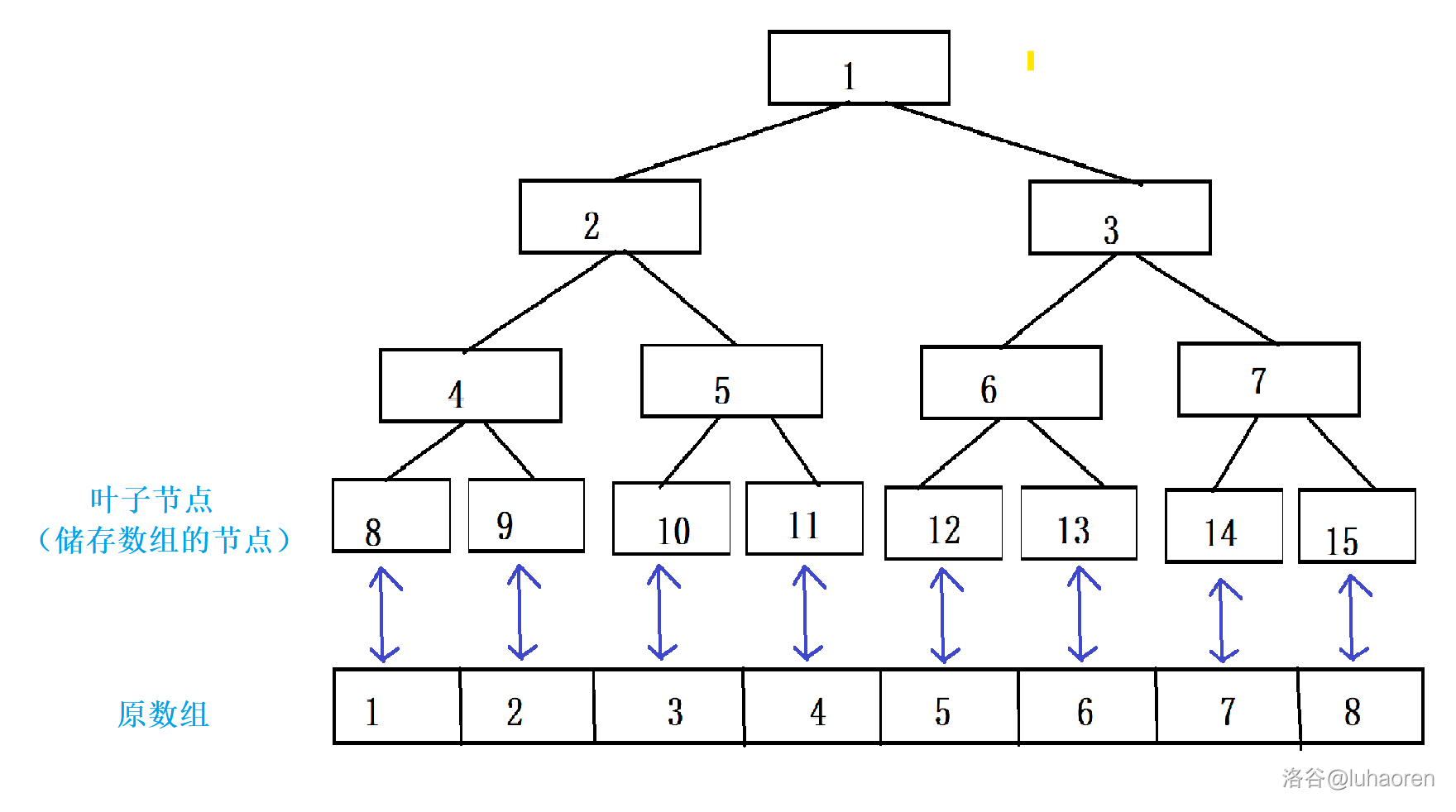
而原陣列中的數位編號也恰恰是連續的，所以二者之間有一個對應關係。

仔細觀察，發現兩者序號之差竟然是一個定值。

所以，我們就可以快速地找到數位線上段樹中的位置，即x+N（N為差值）。

而這個\(N\)就應該是線段樹中拋去葉子節點之外的節點的數量。

為了方便，我們約定，無論樹有沒有那麼大，我們都把\(N\)看作\(n\)，無資料的葉節點空置即可。

這樣我們就可以通過迴圈的方式，完成線段樹的初始化。

建樹程式碼

int tr[N*4];//zkw線段樹不用維護子區間，直接開陣列就行
int n,m;
void build(){
	cin>>n>>m;
	for(int i=n+1;i<=2*n;i++) cin>>tr[i];//直接讀入到葉子節點裡
	for(int i=n-1;i>=1;i--) tr[i]=tr[i*2]+tr[i*2+1];//自底向上更新
}

建樹才三行程式碼，還包括了讀入，zkw線段樹是不是很神奇？

單點修改&區間查詢

單點修改

找到了數位線上段樹中的位置，怎麼更新它的父節點呢？

按照堆式儲存的特點，節點的父節點就應該是\(x/2\)（x是這個節點）

那麼從葉子節點開始，一步步地向上爬，更新，就完成了一次單點修改。

這也是zkw線段樹的一個特色——自底向上。

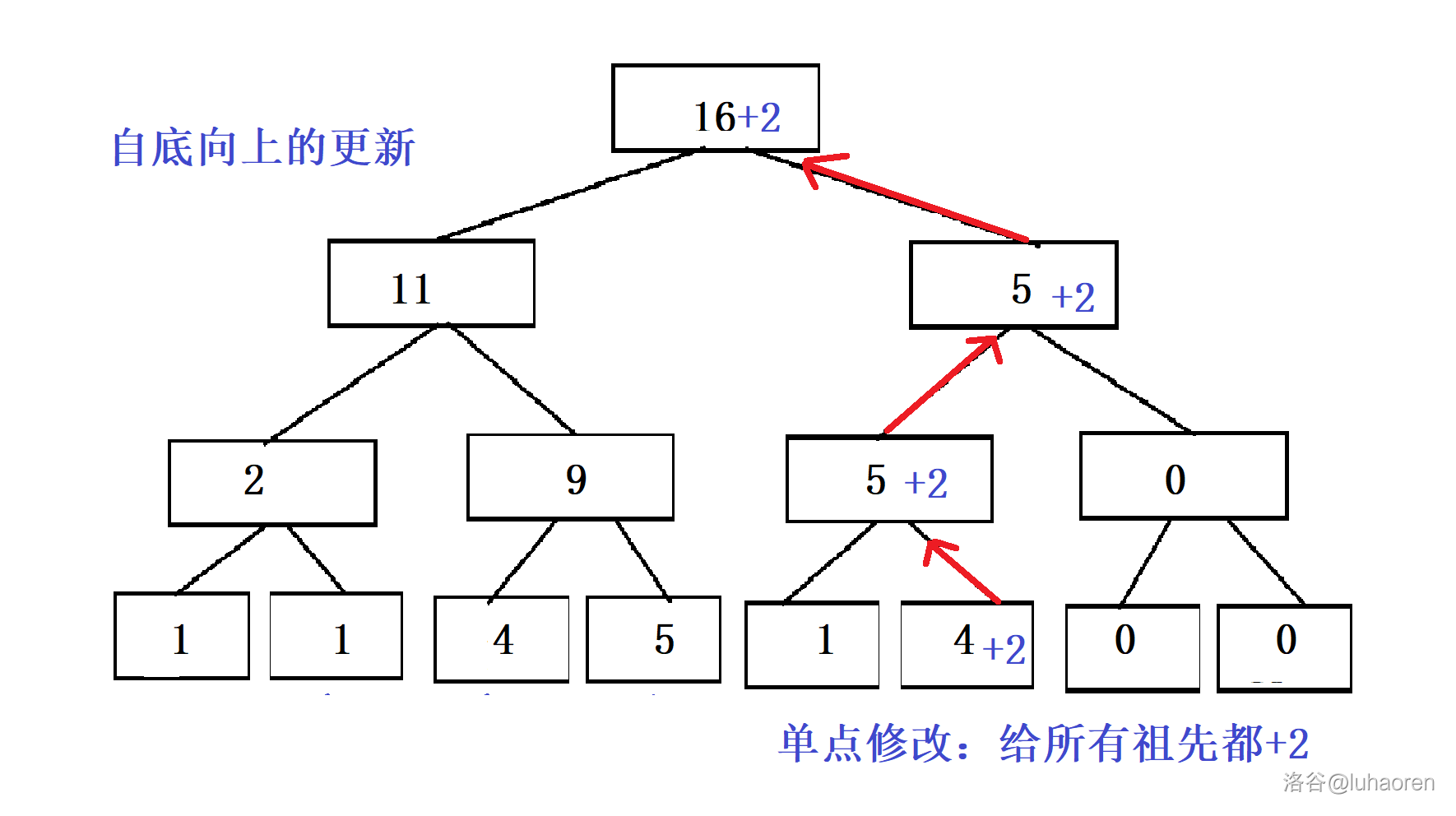
單點修改程式碼

inline void change(int x,int k){//給x加上k
	for(int i=x+=n;i;i/=2) tr[i]+=k;//自底向上更新
}

看完單點修改，相信大家已經會了單點查詢，那就是：

單點查詢程式碼

inline int query_one(int x){//查詢x值
	return tr[x+n];
}

區間查詢

接下來思考，如何做到區間查詢呢？

如圖，以查詢\([3,6]\)區間之和為例，我們先設兩個指標\(p,q\)，讓\(p=l-1,q=r+1\)。

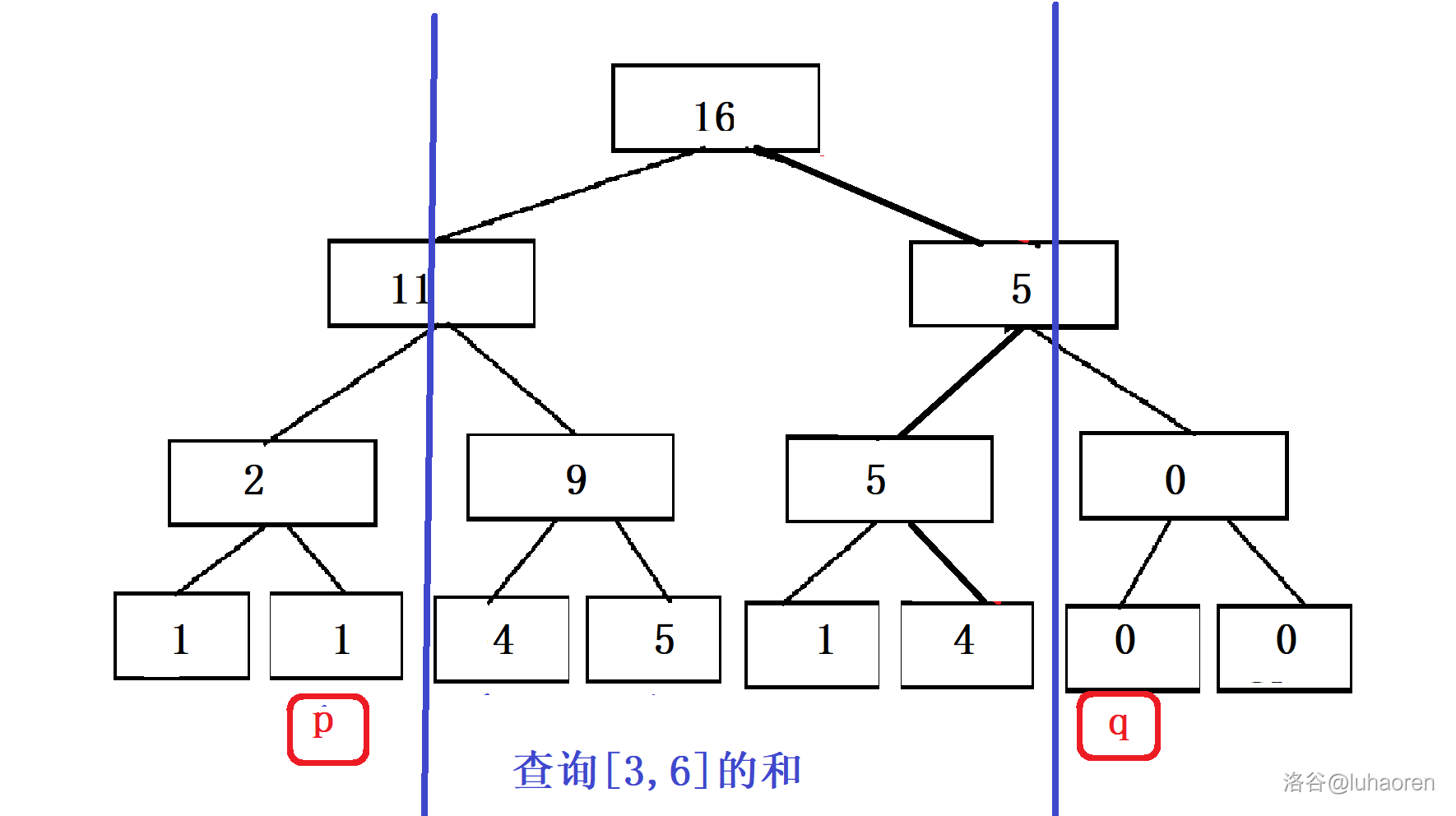
然後讓\(p\)和\(q\)一直往上跳，直到兩個指標的父節點相同。

有沒有發現，這兩個指標籠罩的地方，就是我們要查詢的區間。

多觀察一會，我們會發現一個規律：

1. \(p\)指向的節點是左兒子，那麼答案加上右兒子的值

2. \(q\)指向的節點是右兒子，那麼答案加上左兒子的值

區間查詢程式碼

inline int query(int l,int r){
	int ans=0;
	for(int p=l-1,q=r+1;p/2!=q/2;p/=2,q/=2){
		if(!(p%2)) ans+=tr[p+1];//第一種情況
		if(q%2) ans+=tr[q-1];//第二種情況
	}
	return ans;
}

習題

1. P3374 單點修改，區間查詢 用zkw線段樹再做一遍

區間修改&單點查詢

區間修改

zkw線段樹也支援區間修改，但是由於很難做到pushdown，所以zkw線段樹採用標記永久化的方式進行區間修改。

區間修改和區間查詢差不多，也是維護兩個指標，不同點是：從累加答案變成修改懶標記。

區間修改程式碼

void uplate(int l,int r,int k){//給l,r區間內的數加上k
	for(int p=l-1,q=r+1;p/2!=q/2;p/=2,q/=2){
		if(!(p%2)) add[p+1]+=k;
		if(q%2) add[q-1]+=k;
	}
}

單點查詢

在有懶標記的情況下，單點查詢也變得不同。

首先自底向上累加所有祖宗節點的懶標記，然後再加上本身的值。

單點查詢程式碼

inline int query_one(int x){//查詢x值
	int sum=0;
	for(int i=x+=n;i;i/=2) sum+=add[i];
	return tr[x+n]+add[i];
}

習題

1. P3372 線段樹1
   用zkw線段樹做一遍
2. P3368 樹狀陣列2
   區間修改，單點查詢

可持久化線段樹

可持久化線段樹 ，顧名思義，就是可以保留每一個歷史版本，並且支援在歷史版本上進行操作的線段樹。

為什麼要可持久化呢?有的時候離線維護掃描線之類的東西時，就需要在時間軸裡穿梭，這就需要歷史版本；權值線段樹如果能可持久化，就可以維護區間的資料，達到靜態樹套樹的效果。

那麼如何可持久化呢？

首先，最暴力的做法就是，開\(n\)個線段樹，但是這樣肯定會爆空間，所以，我們得想點別的招。

如圖，這是一個普通的線段樹。

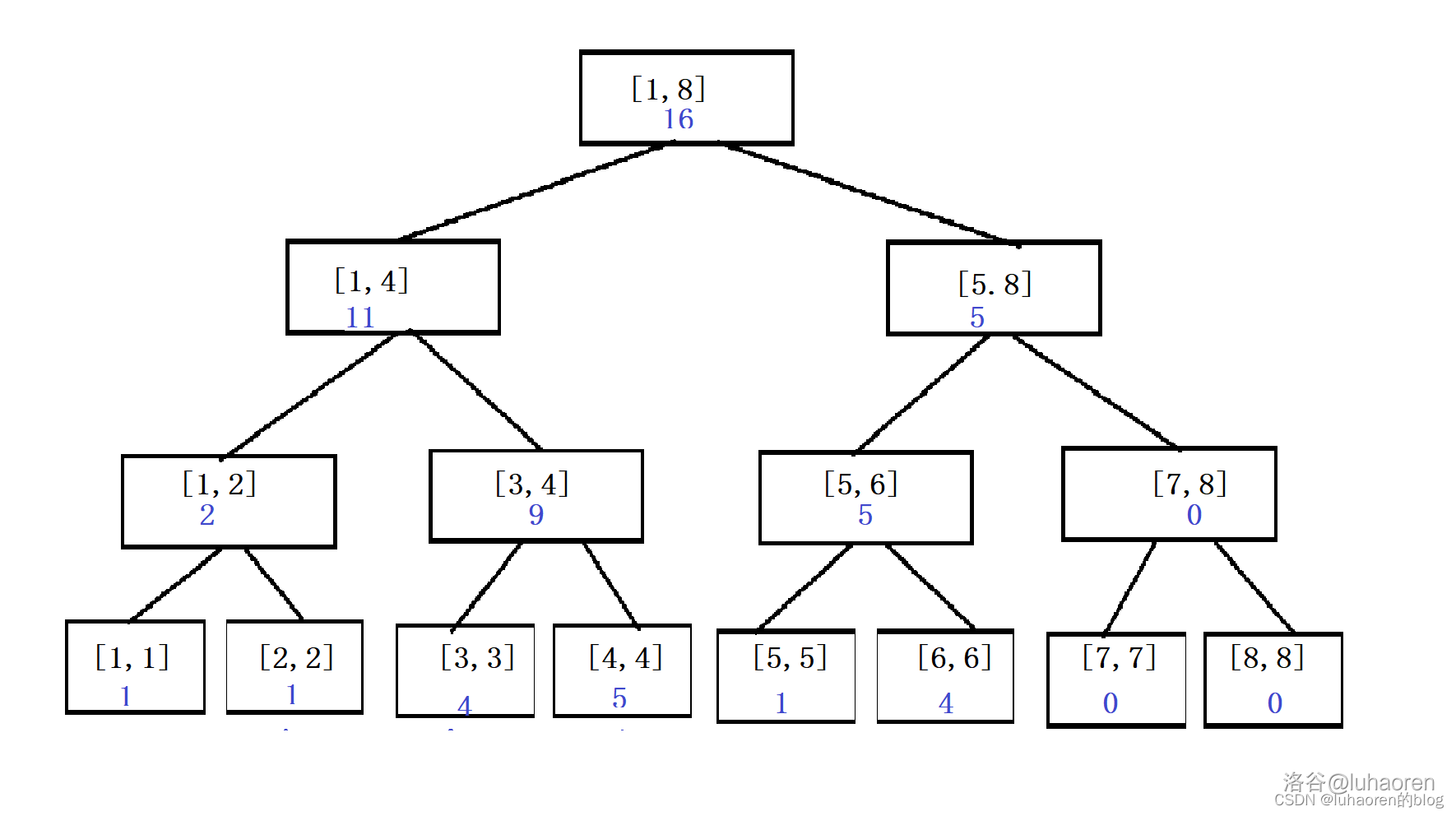
我們把第7個數加上3，如圖。

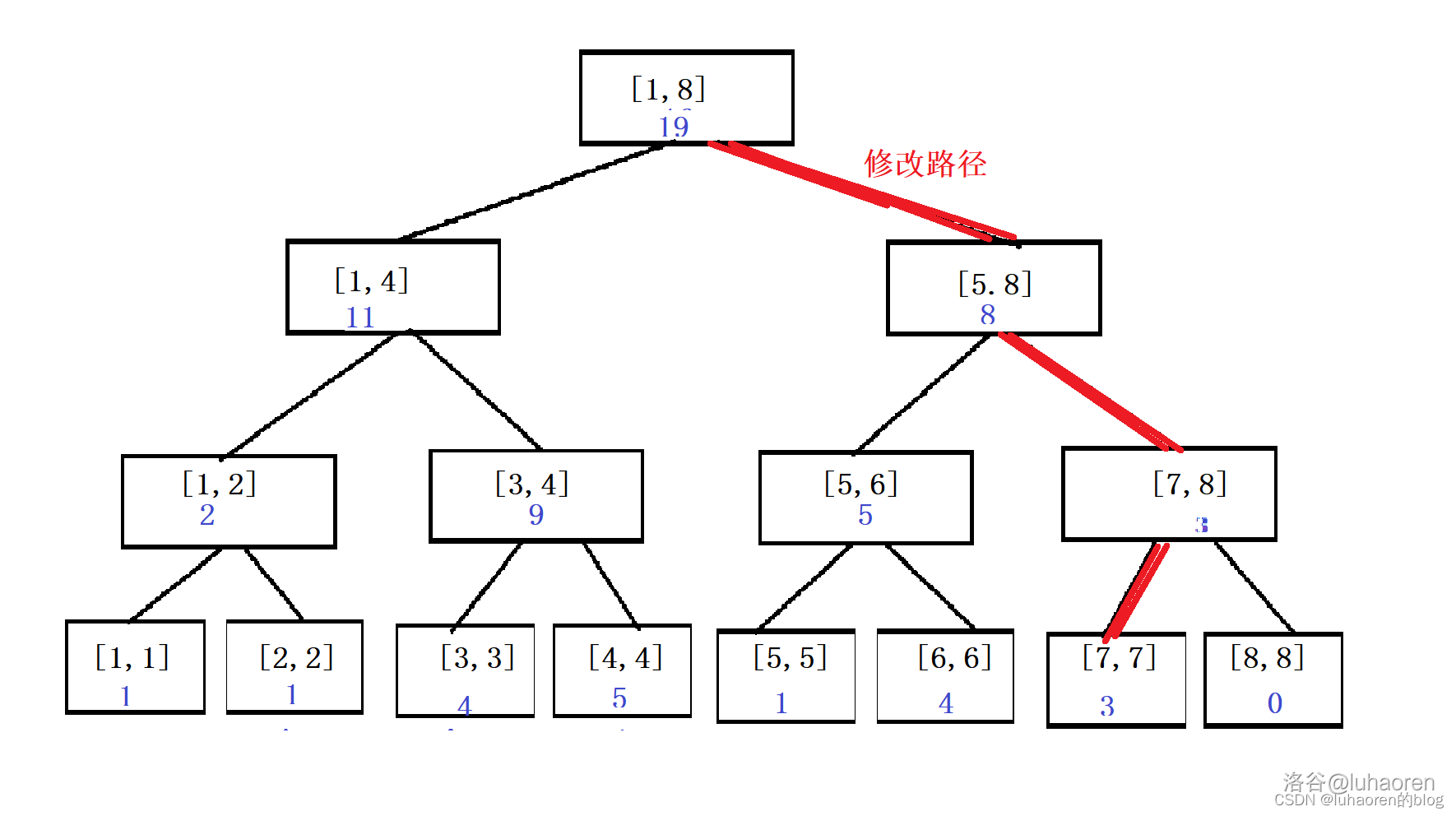
仔細觀察，就會發現，被修改的節點實際上只是一條鏈，長度為\(\log n\)。

於是，著名神犇hjt突發奇想，如果每次修改只維護一條鏈的話，空間複雜度就變成\(O(n+m\log n)\)了呀。

於是就有了可持久化線段樹，也叫主席樹（能猜到原因吧）

如圖，在可持久化線段樹裡給第7個數加上3。

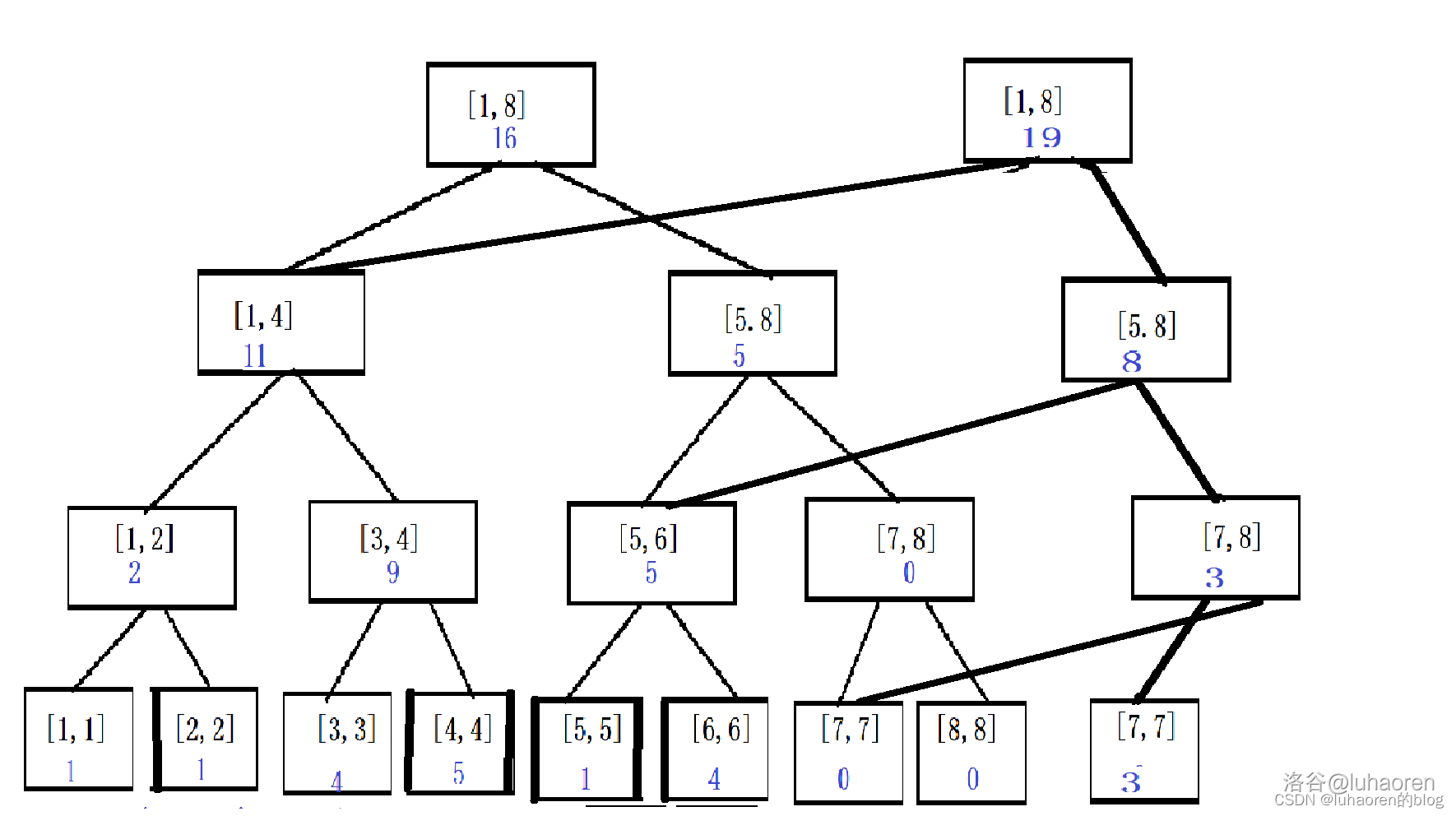
從這個圖中，我們可以看出可持久化線段樹的訣竅在於——複用歷史版本的節點。

可持久化線段樹只會增加需要修改的節點，而不需要修改的節點就可以使用以前的結構，這種思想被稱為「函數語言程式設計「，所以可持久化線段樹也叫」函數式線段樹「。

核心程式碼

void build(int &x,int l,int r){
	//建樹操作，即第0個版本，所有版本複用的基礎
	x=++tot;//可持久化線段樹使用動態開點的方式，因此需要有lsrs陣列儲存左右兒子節點
	if(l==r){
		tr[x]=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(ls[x],l,mid),build(rs[x],mid+1,r);
	//因為x是參照形式，所以會直接給lsrs陣列賦值
}
void change(int u,int &x,int l,int r,int k,int p){
	x=++tot;
	tr[x]=tr[u],ls[x]=ls[u],rs[x]=rs[u];
	//複製原節點
	if(l==r){
		tr[x]=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) change(ls[u],ls[x],l,mid,k,p);//修改左兒子，右兒子直接複用原節點的右兒子
	else change(rs[u],rs[x],mid+1,r,k,p);//同理
}

例題6：可持久化陣列

洛谷P3919

維護這樣的一個長度為 \(N\) 的陣列，支援如下幾種操作：

1. 在某個歷史版本上修改某一個位置上的值
2. 存取某個歷史版本上的某一位置的值

此外，每進行一次操作（對於操作\(2\)，即為生成一個完全一樣的版本，不作任何改動），就會生成一個新的版本。版本編號即為當前操作的編號（從\(1\)開始編號，版本\(0\)表示初始狀態陣列）

題目分析

很明顯，這一個可持久化線段樹模板題，需要單點修改，單點查詢，套用模板即可。

AC程式碼

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10,M=5e7+10;//可持久化線段樹大概需要O(4n+mlogn)的空間，一般直接開N<<5
int tr[M],root[N],ls[M],rs[M],tot=0,a[N];
void build(int &x,int l,int r){
	x=++tot;
	if(l==r){
		tr[x]=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(ls[x],l,mid),build(rs[x],mid+1,r);
}
void change(int u,int &x,int l,int r,int k,int p){
	x=++tot;//動態開點
	tr[x]=tr[u],ls[x]=ls[u],rs[x]=rs[u];//複製節點
	if(l==r){
		tr[x]=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) change(ls[u],ls[x],l,mid,k,p);
	else change(rs[u],rs[x],mid+1,r,k,p);
}
int query(int x,int l,int r,int k){
	if(l==r) return tr[x];
	int mid=(l+r)/2;
	if(k<=mid) return query(ls[x],l,mid,k);
	return query(rs[x],mid+1,r,k);
}
int n,m;
int main(){
	scanf("%d%d",&n,&m);//本題稍微有點卡常，需要用printf和scanf
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(root[0],1,n);
	for(int i=1;i<=m;i++){
		int v,opt,k,p;
		scanf("%d%d",&v,&opt);
		if(opt==1){
			scanf("%d%d",&k,&p);
			change(root[v],root[i],1,n,k,p);
		}
		else{
			scanf("%d",&k);
			printf("%d\n",query(root[v],1,n,k));
			root[i]=root[v];
		}
	}
}

例題7：靜態區間第k小

洛谷P3834

給定\(n\) 個整數構成的序列 \(a\)，將對於指定的閉區間 \([l,r]\) 查詢其區間內的第 \(k\) 小值。

題目分析

如果沒有區間操作，查詢第k小可以用權值線段樹實現，如果有要支援區間操作呢？

我們建一顆可持久化權值線段樹，如圖，把\(\{2,4,1,3\}\)這個數列的數依次插入。

仔細觀察，就會發現第\(i\)棵樹儲存著前\(i\)個數的資訊（設初始化的樹為第\(0\)棵）

也就是說，這個可持久化線段樹可以說是數列的「字首樹」。

你能想到什麼？

可持久化線段樹滿足區間可加減性，所以我們可以用字首和的方式找出維護\([l,r]\)個數的資訊的樹。

也就是拿出第\(l-1\)棵樹和第\(r\)棵樹，兩者相減，結果就是\([l,r]\)的資訊。

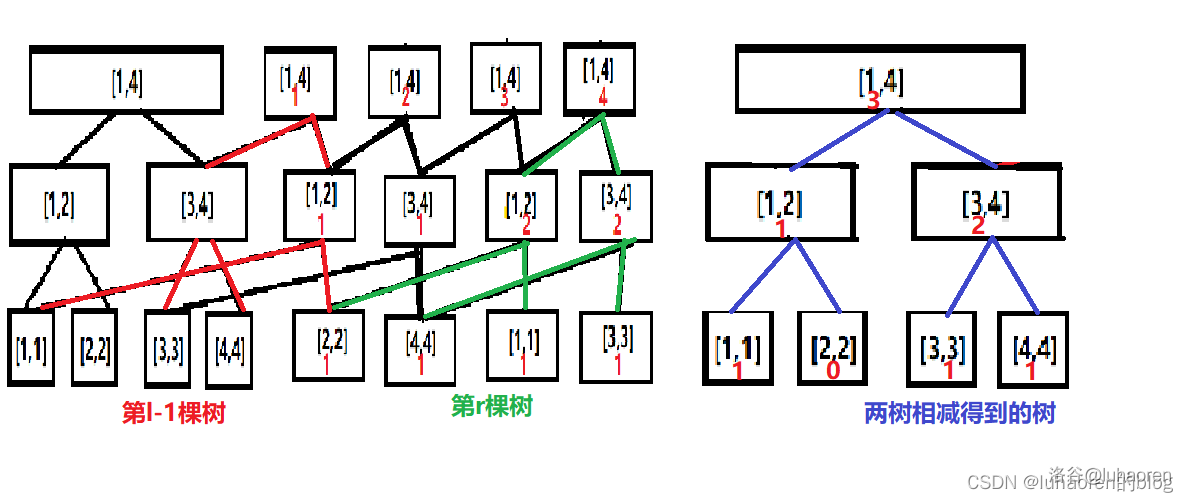
而在相減後的樹上找第k小相信大家都已經會了。

那麼就可以寫出程式碼了！

注：這題資料很水，題面給\(|a_i |\le 10^9\)，但實際上的資料範圍是\(0 \le a_i \le 10^6\)，甚至不需要離散化的優化，就可以過。

AC程式碼

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int tr[N<<5],ls[N<<5],rs[N<<5],root[N],tot=0;
void build(int &x,int l,int r){
    //建樹
	x=++tot;
	if(l==r) return;
	int mid=(l+r)/2;
	build(ls[x],l,mid),build(rs[x],mid+1,r);
}
void insert(int u,int &x,int l,int r,int k){
	x=++tot;//動態開點
	tr[x]=tr[u]+1,ls[x]=ls[u],rs[x]=rs[u];//複製該節點的所有資訊（可以直接在節點上+1，否則還得pushuo一遍）
	if(l==r)  return; 
	int mid=(l+r)/2;
	if(k<=mid) insert(ls[u],ls[x],l,mid,k);
	else insert(rs[u],rs[x],mid+1,r,k);
}
int query(int u,int v,int l,int r,int k){
	int mid=(l+r)/2,lx=tr[ls[v]]-tr[ls[u]];//兩顆樹資訊相減得到的左兒子資訊
	if(l==r) return l;//如果只有一個數，第幾大都是這個數了，直接返回
	if(k<=lx) return query(ls[u],ls[v],l,mid,k);
	return query(rs[u],rs[v],mid+1,r,k-lx);//二分查詢第k小
}
int n,m;
int main(){
	cin>>n>>m;
	build(root[0],0,1e6);//建樹
	for(int i=1;i<=n;i++){
		int t;
		cin>>t;
		insert(root[i-1],root[i],0,1e6,t);
	}
	while(m--){
		int l,r,k;
		cin>>l>>r>>k;
		cout<<query(root[l-1],root[r],0,1e6,k)<<endl;
	}
}

實際上，這份程式碼在除了洛谷以外的其它OJ上是AC不了的，因為題面上\(|a_i|\le 10^9\)的資料範圍使程式碼必須要有離散化的優化，這裡給出優化程式碼。

//其他部分和前面無異，這以後是離散化程式碼
int n,m,tt=0;
map<int,int>mp;//使用map離散化，使用sort離散化也可以
int val[N],a[N];
int main(){
    cin>>n>>m;
    build(root[0],1,n);
    for(int i=1;i<=n;i++){
        cin>>a[i];
        mp[a[i]]=0;
    }
    for(auto it:mp){
    //map會自己排序，在遍歷的過程中標上對映後的序號
        mp[it.first]=++tt;
        val[tt]=it.first;
    }
    for(int i=1;i<=n;i++) insert(root[i-1],root[i],1,n,mp[a[i]]);
    while(m--){
        int l,r,k;
        cin>>l>>r>>k;
        cout<<val[query(root[l-1],root[r],1,n,k)]<<endl;
    }
}

習題

1. 洛谷P3402 可持久化並查集
   注意並查集的合併操作
2. [POI2014] KUR-Couriers
   維護區間絕對眾數，有亂搞做法

U.P.D

2023年2月17日 初稿，大概兩千多字。

2023年6月？ cry拿去學，發現了一堆錯誤（比如程式碼寫了個tr[x]=tr[x*2]+tr[x*2]）。

2023年7月3日 開始重寫。

2023年7月6日 寫完基礎部分

2023年7月8日 增加了權值線段樹

2023年7月9日 挪到了洛谷上，把圖片傳到了洛谷圖床上。增加了權值線段樹的習題。

2023年7月9日 增加了zkw線段樹

2023年7月11日 增加了可持久化線段樹

參考資料

1. oiwiki關於線段樹儲存空間的證明

2. 洛穀日報·線段樹

3. 標記永久化

4. 標記永久化

5. 洛穀日報·權值線段樹到主席樹

6. P3369普通平衡樹題解

7. 統計的力量（zkw課件）

8. 同機房巨佬的部落格

9. 洛穀日報·zkw線段樹

10. zkw的課件