參考資料：
Expected Improvement formula for Bayesian Optimisation
通俗科普文：貝葉斯優化與SMBO、高斯過程迴歸、TPE
理解貝葉斯優化
 A Tutorial on Bayesian Optimization

貝葉斯優化是一種求解函數最優值的演演算法，它最普遍的使用場景是在機器學習過程中對超引數進行調優。貝葉斯優化演演算法的核心框架是SMBO (Sequential Model-Based Optimization)，而貝葉斯優化（Bayesian Optimization）狹義上特指代理模型為高斯過程迴歸模型的SMBO。

問題介紹

\[\max_{x\in A}f(x) \]

輸入：\(x\in R^d\)，一般\(d\le20\)，即引數在20個以內。
可行集（feasible set）\(A\)： 一般是超多邊形（\(x\in R^d: a_i\le x_i \le b_i\)）或d維的simplex（\(x\in R^d: \sum_ix_i=1\)）
在使用貝葉斯優化時，目標函數\(f\)：
- 需要是連續函數
- 評估成本昂貴，能允許執行的次數有限
- 是黑盒，公式/特徵未知，例如：不是凹函數、線性函數之類的。
- 因為不對函數做任何假設，所以只能存取f，不能存取其一階、二階導數。
- 可以有噪聲，但需要假設每個觀測值的噪聲是獨立同分布，均值為0，方差恆定。

SMBO (Sequential Model-Based Optimization)

SMBO是一套優化框架，也是貝葉斯優化所使用的核心框架。它有兩個重要組成部分：

一個代理模型（surrogate model），用於對目標函數進行建模。代理模型通常有確定的公式或者能計算梯度，又或者有已知的凹凸性、線性等特性，總之就是更容易用於優化。更泛化地講，其實它就是一個學習模型，輸入是所有觀測到的函數值點，訓練後可以在給定任意\(x\)的情況下給出對\(f(x)\)的估計。
一個優化策略（optimization strategy），決定下一個取樣點的位置，即下一步應在哪個輸入\(x\)處觀測函數值\(f(x)\)。通常它是通過採集函數（acquisition function） 來實現的：
採集函數通常是一個由代理模型推出的函數，它的輸入是可行集（feasible set）\(A\)上的任意值，輸出值衡量了每個輸入\(x\)有多值得被觀測。通常會從以下兩方面考慮：
- 有多大的可能性在x處取得最優值
- 評估x是否能減少貝葉斯統計模型的不確定性
  採集函數通常也是容易求最優值的函數（例如：有公式/能算梯度，等），下一個取樣點就是可行集上的最大值點，即使採集函數的取最大值的點。

該框架的主要流程是：

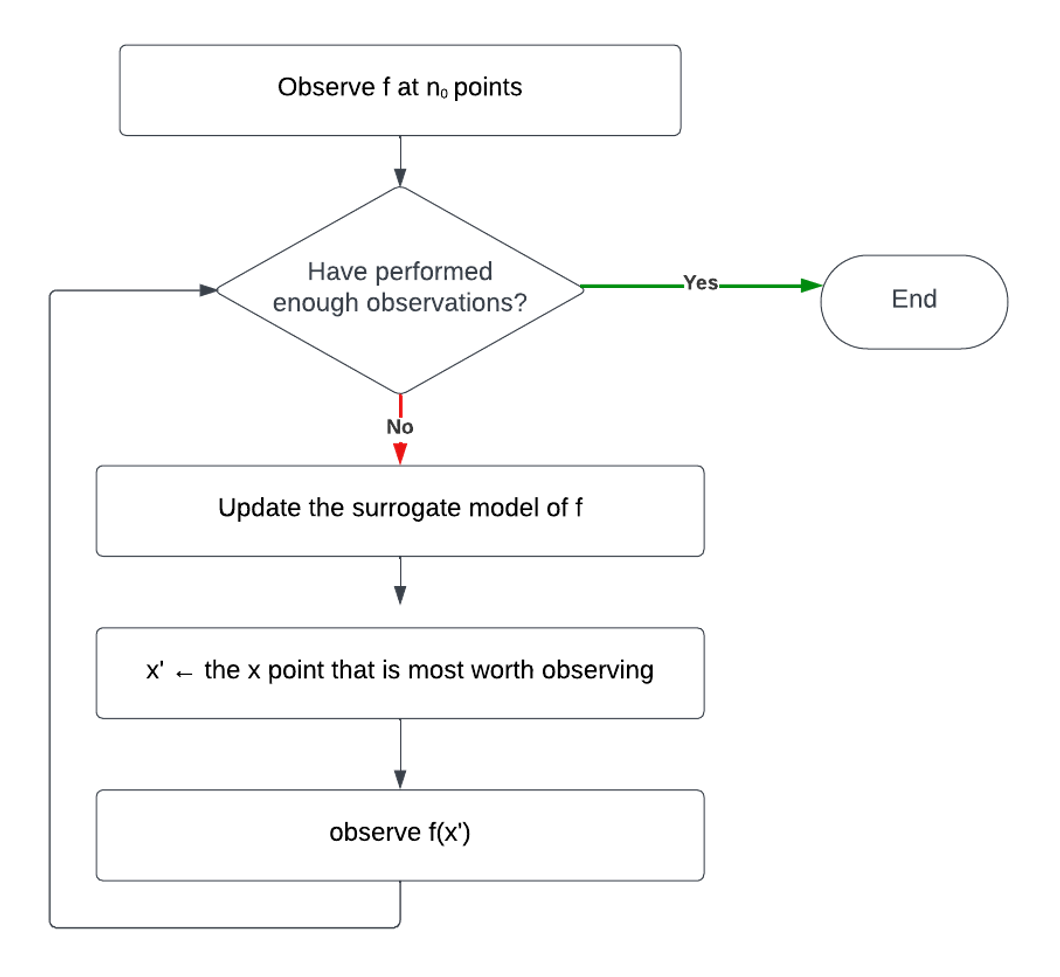
代理模型（Surrogate Model）

代理模型可以有很多，高斯過程、隨機森林……等等。其中，貝葉斯優化（Bayesian Optimization） 狹義上特指代理模型為高斯過程迴歸模型的SMBO。

隨機過程

隨機過程（Stochastic/Random Process）可以理解為一系列隨機變數的集合。更具體地說，它是概率空間上的一族隨機變數\(\{X(t),t\in T\}\)，其中是t引數，而T又被稱作索引集（index set），它決定了構成隨機過程的隨機變數的個數，大部分情況下，隨機變數都是無限個的。

當\(T=\{0,1,2,...\}\)時稱之為隨機序列或時間序列
引數t經常被解釋為時間。
引數空間T是向量集合時，隨機過程\(\{X(t),t\in T\}\)稱為隨機場。
隨機過程有時也被稱為隨機函數（Random Function），因為它也可以被理解為函數值是隨機變數的函數。

\(X(t)\)表示系統在時刻t所處的狀態。的所有可能狀態構成的集合為狀態空間，記為S。

隨機過程的直觀理解

隨機過程的直觀含義是我們在 t=0 時刻（此時此刻）來考慮未來每個時間點會發生的情況。

例如，當我們把\(t\)解釋為時間，而\(X(t)\)解釋為粒子位置時，隨機過程就可以被直觀地理解為粒子的一種隨機運動，它在每個時刻下的位置都是隨機的，並且不同時刻\(t_1\)和\(t_2\)對應的\(X(t_1)\)和\(X(t_2)\)是相關的，它們的相關性由協方差\(cov[X(t_1),X(t_2)]\)定義。

辨析隨機變數和隨機函數

假設：

\(x\)是一個變數
\(X\)是一個隨機變數，它服從一個概率分佈\(P(X<t)=p(t)\)
\(f\)是一個函數，例如：\(f(x)=x+1\)
\(g\)是一個隨機函數

那麼有：

\(f(x)\)代表一個因變數，當\(x\)確定時，也確定。例如：\(f(x)=x+1\)，\(f(1)=2\)
\(f(X)\)代表一個隨機變數，它的隨機性是隨機變數\(X\)帶來的，所以它的概率分佈也跟的概率分佈有關。例如：\(f(x)=x+1\)，\(P(f(X)<t)=P(X+1<t)=P(X<t-1)\)
\(g(x)\)也代表一個隨機變數，但它的隨機性是隨機過程\(g\)帶來的。

高斯過程

高斯過程（Gaussian Process）是一類隨機過程\(\{F(x),x\in A\}\)，它的任意n維分佈\(\{F(x_1),...,F(x_n)\}\)（n也是任意的）都服從多元正態分佈，即：對任意有限個\(x_1,...,x_n\in A\)，\(F(x_1),...,F(x_n)\)的任意線性組合\(a_1F(x_1)+...+a_nF(x_n)\)都是一個正態分佈。

正如一個正態分佈可以通過指定均值和方差來確定，一個高斯過程可以通過指定均值函數 \(m(x)\) 和協方差函數 \(K(x,x')\)唯一確定：

\[\begin{align*} m(x)&=E[F(x)] \\ K(x,x')&=E[(F(x)-m(x))(F(x')-m(x'))] \end{align*} \]

則高斯過程可以表示為：

\[F(x)\sim GP(m(x), K(x, x')) \]

均值函數定義了每個索引\(x\)對應的隨機變數（同時也是正態分佈變數）\(F(x)\)的均值；而協方差函數不僅定義了每個索引的方差\(K(x,x')\)，還定義了任意兩個索引\(x_1\)、\(x_2\)對應的隨機變數\(F(x_1 )\)\(F(x_1)\)\(F(x_2)\)之間的相關性\(K(x_1, x_2)\)。

在高斯過程模型裡，協方差函數也被稱作核函數（Kernel function）。

高斯過程迴歸

高斯過程迴歸（Gaussian Process Regression）就是使用高斯過程模型\(F(x)\)去擬合目標函數\(f(x)\)。

讓我們先回顧一下，使用正態分佈\(N(\mu,\sigma^2)\)去擬合一個隨機變數X的步驟：

建模前，我們知道正態分佈的均值和標準差都是常數，分別假設為\(\mu\) 和\(\sigma^2\)。

對隨機變數X進行t次取樣，得到觀測值\(x_1,...,x_t\)（簡記為\(x_{1:t}\)）

根據觀測值計算出最優的\(\mu\) 和\(\sigma\)值，由此確定最終正態分佈的樣子，從而完成對X的擬合

高斯過程迴歸也是類似的：

建模前，我們需要事先指定好均值函數 \(m(x)\) 和協方差函數 \(K(x,x')\)，它定義了高斯過程\(F(x)\)的先驗分佈。
- 有一些超引數會存在於均值函數和協方差函數中。前面提到的正態分佈擬合就像是一種簡化：\(m(x)=\mu\)，\(K(x,x')=\sigma^2\)，這裡\(\mu\) 和\(\sigma\)可以被理解為是兩個超引數。
選擇t個取樣索引\(x_1,...,x_t\)（簡記為\(x_{1:t}\)），得到目標函數的觀測值\(f(x_1),...,f(x_t)\)（簡記為\(f(x_{1:t})\)），它們同樣也是高斯過程裡對應的隨機變數\(F(x_1),...,F(x_t)\) \(F(x_1),...,F(x_t)\)\(F(x_{1:t})\)）的觀測值
根據觀測值調整均值函數和協方差函數裡的超引數，由此確定最終高斯過程的樣子，從而完成對函數\(f(x)\)的擬合。

常用均值函數

常數函數

\[m(x)=\mu \]
這裡\(\mu\)是一個超引數。即使將均值統一設定為常數，因為有方差的作用，依然能夠對資料進行有效建模。
parametric function

\[m(x)=\mu + \sum_{i=1}^P\beta_i\Psi_i(x) \]
這裡\(\mu\)，\(\beta_i\)都是超引數。

常用協方差函數

在迴歸任務裡，由於目標函數f是連續函數，因此對協方差函數最基礎的要求是有該性質：

x與x’距離越近時，f(x)與f(x’)相關性越大。即：

\[K(x,x_1)>K(x,x_2), \text{ if } ||x-x_1||<||x-x_2|| \]

常用協方差函數有：

Power exponential / Gaussian

\[K(x,x')=\alpha_0 e^{-||x-x'||^2} \]
這裡\(||x-x'||^2=\sum_{i=1}^d\alpha_i(x_i-x'_i)^2\)，不是標準的L2正規化的寫法，d是自變數x的維度數量，即引數的個數。\(\alpha_{0:d}\)是d+1個超引數。
Màtern

\[K(x,x')=\alpha_0 \frac{2^{1-\nu}}{\Gamma(\nu)}(\sqrt{2\nu}||x-x'||)^\nu K_\nu(\sqrt{2\nu}||x-x'||) \]
\(K_\nu\)是modified Bessel functions of the second kind。

如何計算超引數

採用最大後驗估計（MAP，Maximum A Posterior estimate），選擇在觀測值已知的情況下最可能的超引數值。

\[\hat{\eta}=\text{argmax}_{\eta}{P(\eta|F(x_{1:t})=f(x_{1:t}))} \]

\(\eta\)代表超引數集合，\(P(\eta|F(x_{1:t})=f(x_{1:t}))\)代表在得到所有觀測值的情況下，超引數的概率分佈。

使用貝葉斯公式進行轉換：

\[P(\eta|F(x_{1:t})=f(x_{1:t}))=\frac{P(F(x_{1:t})=f(x_{1:t})|\eta)P(\eta)}{P(F(x_{1:t})=f(x_{1:t}))} \]

這也是以高斯過程為代理模型的SMBO又被叫做貝葉斯優化的原因。

由於分母與超引數無關，因此只需要最大化分子：

\[\hat{\eta}=\text{argmax}_{\eta}{P(F(x_{1:t})=f(x_{1:t})|\eta)P(\eta)} \]

\(P(F(x_{1:t})=f(x_{1:t})|\eta)\)是給定引數的情況下，得到所有觀測值的概率。

\(P(\eta)\)是超引數取值的先驗概率，在某些問題，可以假設某些引數更可能被使用。但更常見的情況是假設其為等概率分佈，那麼MAP就是退化為最大似然估計（MLE, Maximum Likelihood Estimate），即選擇使觀測值最可能出現的超引數值：

\[\hat{\eta}=\text{argmax}_{\eta}{P(F(x_{1:t})=f(x_{1:t})|\eta)} \]

由於在高斯過程中，觀測點\(x_{1:t}\)對應的隨機變數構成的多維隨機變數[\(F(x_1),...,F(x_t)\)]（簡記作\(F(x_{1:t})\)）服從多元正態分佈。其中，

分佈的均值是一個t維向量：\(\mathbf{\mu_t}=[m(x_1),...,m(x_t)]\)。其中，\(m(x_i)\)代表第i個隨機變數\(F(x_i)\)的期望/均值\(E[F(x_i)]\)。
分佈的協方差矩陣是一個\(t\times t\)的矩陣，記作：

\[\mathbf{\Sigma_t} =\begin{bmatrix} K(x_1,x_1)&...&K(x_1,x_t) \\ ...&...&... \\ K(x_t,x_1)&...&K(x_t,x_t) \\ \end{bmatrix} \]

概率密度函數為

\[L(x_{1:t}|\eta)=\frac{1}{\sqrt{(2\pi)^t|\mathbf{\Sigma_t}|}}e^{-\frac{1}{2}(x_{1:t}-\mathbf{\mu_t})^T\mathbf{\Sigma_t}^{-1}(x_{1:t}-\mathbf{\mu_t})} \]

由於觀測點\(x_{1:t}\)是已知的，因此，它是一個以超引數為變數的函數，我們可以選擇使該概率（密度）最大化的超引數值。

轉化為對數似然函數：

\[\ln{L(x_{1:t}|\eta)}=-\frac{1}{2}[t\ln{2\pi}+\ln{|\mathbf{\Sigma_t}|}+(x_{1:t}-\mathbf{\mu_t})^T\mathbf{\Sigma_t}^{-1}(x_{1:t}-\mathbf{\mu_t})] \]

要最大化它，即是最小化：

\[M(x_{1:t}|\eta)=\ln{|\mathbf{\Sigma_t}|}+(x_{1:t}-\mathbf{\mu_t})^T\mathbf{\Sigma_t}^{-1}(x_{1:t}-\mathbf{\mu_t}) \]

它是一個已知公式可以求梯度的函數，因此在程式設計中可以通過梯度下降等方法去求解其最優值。

預測\(f(x)\)

在SMBO框架下，代理模型預測的不僅僅是函數值\(f(x)\)，而是它的後驗分佈\(F(x)|F(x_{1:t})=f(x_{1:t})\)，即，在已知t個觀測點的值的情況下，\(f(x)\)取不同值的概率。

由於在高斯過程裡，也符合多元正態分佈，因此就是多元正態分佈的條件分佈（或邊緣分佈）。這個分佈服從正態分佈，其均值和方差如下：

\[\begin{align*} F(x)|F(x_{1:t})=f(x_{1:t})&\sim N(\mu, \sigma^2) \\ \mu(x) &= K(x,x_{1:t})K(x_{1:t},x_{1:t})^{-1}(f(x_{1:t})-m(x_{1:t}))+m(x)\\ \sigma^2(x)&=K(x,x)-K(x,x_{1:t})K (x_{1:t}, x_{1:t})^{-1}K(x_{1:t},x)\end{align*} \]

其中，

\[m(x_{1:t})=[m(x_1),...,m(x_t)] \]

\[K(x_{1:t}, x_{1:t}) =\begin{bmatrix} K(x_1,x_{1:t}) \\ ... \\ K(x_t,x_{1:t}) \end{bmatrix} =\begin{bmatrix} K(x_1,x_1)&...&K(x_1,x_t) \\ ...&...&... \\ K(x_t,x_1)&...&K(x_t,x_t) \\ \end{bmatrix} \]

由於均值函數\(m(x)\)、協方差函數\(K(x,x')\)都是確定公式的函數，公式裡的超引數也確定下來了，因此\(\mu (x)\)和\(\sigma^2(x)\)都是確定的函數，對任意給定的\(x\)，都可以計算出值來。

通常，我們使用這個後驗分佈的期望/均值來作為函數值\(f(x)\)的預測值：

\[f(x)\leftarrow E[F(x)|F(x_{1:t})=f(x_{1:t})]=\mu(x) \]

【命題1】對任意\(A=[a_1,...,a_t]^T\)，\(i=1,...,t\)，都有\(K(x_i,x_{1:t})K(x_{1:t},x_{1:t})^{-1}A=a_i\)。證明見附錄。

因此，對於已經觀測到的點\(x_i,i=1,...,t\)，我們就有：

\[\begin{align*} \mu(x_i)&=f(x_i)-m(x_i)+m(x_i)=f(x_i)\\ \sigma^2(x_i)&=K(x_i,x_i)-K(x_i,x_i)=0 \\ \end{align*} \]

因此，擬合出來的模型就像這樣：

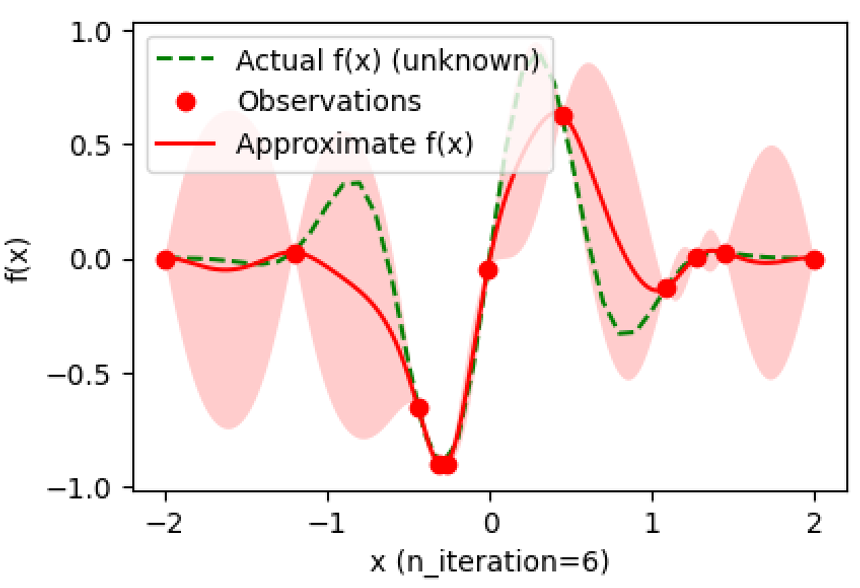
紅色陰影部分是預測的95%置信區間。

採集函數（Acquisition Function）

由於代理模型輸出了函數f的後驗分佈\(F(x)|F(x_{1:t})=f(x_{1:t})\)，我們可以利用這個後驗分佈去評估下一個取樣點應該在哪個位置。由於在採集函數階段我們討論的都是後驗分佈，因此後文中將省略條件部分，提到\(F(x)\)時指的都是\(F(x)|F(x_{1:t})=f(x_{1:t})\)。

通常做法是設計一個採集函數\(A(x, F(x)|F(x_{1:t})=f(x_{1:t}))\)，它的輸入相當於對每個取樣點x進行打分，分數越高的點越值得被取樣。

一般來說，採集函數需要滿足下面的要求：

在已有的取樣點處採集函數的值更小，因為這些點已經被探索過，再在這些點處計算函數值對解決問題沒有什麼用
在置信區間更寬（方差更大）的點處採集函數的值更大，因為這些點具有更大的不確定性，更值得探索
對最大（小）化問題，在函數均值更大（小）的點處採集函數的值更大，因為均值是對該點處函數值的估計值，這些點更可能在極值點附近。

有非常多種採集函數可供選擇，這裡簡單介紹一些作為例子。

Expected Improvement (EI)

當我們已經取樣過t個點之後，總會有一個最優點\(x_m\)，使得：

\[f^*_t=max_{i<t}f(x_i)=f(x_m) \]

假設我們還可以再觀測一輪，得到\(F(x)=f(x)\)，最優點將在\(f(x)\)和\(f^*_t\)之間產生。不妨令

\[[F(x)-f^*_t]^+=\max(0, F(x)-f^*_t) \]

由於現在\([F(x)-f^*_t]^+\)是一個隨機變數，因此我們可以計算它的期望：

\[\begin{align*} EI_t(x)&=E[[F(x)-f^*_t]^+] \\ &=\sigma(x)\phi(\frac{\mu(x)-f^*_t}{\sigma(x)})+(\mu(x)-f^*_t)\Phi(\frac{\mu(x)-f^*_t}{\sigma(x)}) \\ \end{align*} \]

其中，\(\mu(x)\)和\(\sigma(x)\)是正態分佈\(F(x)\)的均值和標準差，即後驗均值和標準差\(\sqrt{\sigma^2(x)}\)。

\(\varphi(x)\)為標準正態分佈的概率密度函數：

\[\varphi(x)=-\frac{1}{\sqrt{2\pi}}g(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \]

而\(\Phi(x)\)為標準正態分佈的分佈函數：

\[\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^xe^{-\frac{t^2}{2}}dt \]

\(EI_t(x)\)也是一個僅以x為自變數的函數，它的最大值點就是下一個取樣點。

\[\hat{x}=\text{argmax}_{x}{EI_t(x)} \]

由於\(EI_t(x)\)有公式，計算不費勁，也可以求梯度，找到它的最大值/極大值有很多種現成的方案可以做到，相比於求原目標函數\(f(x)\)的最值要簡單得多。

\(EI_t(x)\)推導過程

由於\(F(x)\)是正態分佈，因此可以通過其概率密度計算出期望：

\[\begin{align*} EI_t(x)&=E[[F(x)-f^*_t]^+] \\ &=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^{\infty}[z-f^*_t]^+e^{-\frac{(z-\mu)^2}{2\sigma^2}}dz \\ &=\frac{1}{\sigma\sqrt{2\pi}}\int_{f_t^*}^{\infty}(z-f^*_t)e^{-\frac{(z-\mu)^2}{2\sigma^2}}dz \end{align*} \]
令\(k=\frac{z-\mu}{\sigma}\)（也是把隨機變數\(F(x)\)標準化），通過換元法可以得到：

\[\begin{align*} EI_t(x)&=\frac{1}{\sigma\sqrt{2\pi}}\int_{f_t^*}^{\infty}(z-f^*_t)e^{-\frac{(z-\mu)^2}{2\sigma^2}}dz \\ &=\frac{1}{\sqrt{2\pi}}\int_{\frac{f_t^*-\mu}{\sigma}}^{\infty}(\sigma k+\mu-f^*_t)e^{-\frac{k^2}{2}}dk \\ &=\frac{\sigma}{\sqrt{2\pi}}\int_{\frac{f_t^*-\mu}{\sigma}}^{\infty}ke^{-\frac{k^2}{2}}dk+(\mu-f^*_t)(1-\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\frac{f_t^*-\mu}{\sigma}}e^{-\frac{k^2}{2}}dk) \end{align*} \]
由於對\(g(x)=-e^{-\frac{x^2}{2}}\)，有\(g'(x)=xe^{-\frac{x^2}{2}}\)。因此

\[\int_{\frac{f_t^*-\mu}{\sigma}}^{\infty}ke^{-\frac{k^2}{2}}dk=g(\infty)-g(\frac{f_t^*-\mu}{\sigma})=-g(\frac{f_t^*-\mu}{\sigma}) \]
繼續化簡：

\[\begin{align*} EI_t(x)&=E[[F(x)-f^*_t]^+] \\ &=-\frac{\sigma}{\sqrt{2\pi}}g(\frac{f_t^*-\mu}{\sigma})+(\mu-f^*_t)(1-\Phi(\frac{f^*_t-\mu}{\sigma})) \\ &=\sigma\phi(\frac{f^*_t-\mu}{\sigma})+(\mu-f^*_t)[1-\Phi(\frac{f^*_t-\mu}{\sigma})] \\ \end{align*} \]
由於\(\varphi(x)\)是偶函數，且\(\Phi(x)+\Phi(-x)=1\)，則有

\[\begin{align*} EI_t(x)&=E[[F(x)-f^*_t]^+] \\ &=\sigma\phi(\frac{\mu-f^*_t}{\sigma})+(\mu-f^*_t)\Phi(\frac{\mu-f^*_t}{\sigma}) \end{align*} \]

置信區間邊界（Confidence Bound）

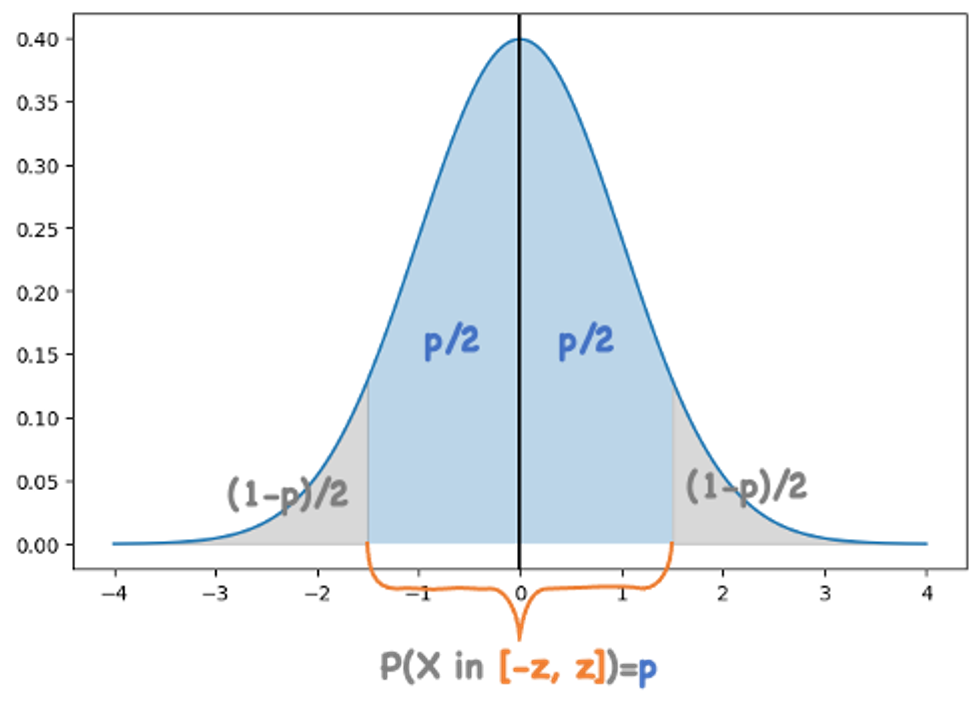
對於標準正態分佈\(X\sim N(0,1)\)，給定任意關於\(x=0\)對稱的區間\([-z,z]\)，可以通過對概率密度進行積分計算出一個概率p，表示符合標準正態分佈的隨機變數的值落在該區間的概率為p。

z和p是一一對應的，可以令\(z=\delta(p)\)，由正態分佈的性質可知，顯然

\[p=\delta^{-1}(z)=P(X<z)=\int_{-\infty}^z\varphi(t)dt=\frac{1+p}{2},\ z\ge 0 \]

\(\delta^{-1}(z)\)就是\(\delta(p)\)的反函數。

假設對於給定置信水平p，隨機變數\(X\)落在置信區間\([-z,z]\)的概率為p，\(z=\delta(p)\)。

由於\(F(x)\sim N(\mu,\sigma)\)，它可以由標準正態分佈轉化過來：

\[F(x)=\sigma X+\mu \]

那麼對於\(F(x)\sim N(\mu,\sigma)\)，當給定置信水平p時，其置信區間就為\([-\mu-z\sigma,\mu+z\sigma]\)。

可以採用該置信區間的邊界作為採集函數。例如，在本文中我們討論最大化f(x)的優化問題，通常就會使用區間的右邊界UCB（Upper Confidence Bound）：

\[UCB_t(x)=\mu(x)+z\sigma(x) \]

其中z是超引數，由想要的置信水平p決定：\(z=\delta(p)\)。

UCB越大，說明在該位置有更高的可能性找到更大的值。

同理，在最小化問題中，通常就會使用區間左邊界LCB（Low Confidence Bound）：

\[LCB_t(x)=-\mu(x)-z\sigma(x) \]

Appendix

命題1證明

【命題1】對任意\(A=[a_1,...,a_t]^T\)，\(i=1,...,t\)，都有\(K(x_i,x_{1:t})K(x_{1:t},x_{1:t})^{-1}A=a_i\)。

令\(K(x_i,x_{1:t})K(x_{1:t},x_{1:t})^{-1}=[z_1,...,z_t]\)，那麼有

\[\begin{align*} K(x_i,x_{1:t})K(x_{1:t},x_{1:t})^{-1}K(x_{1:t},x_{1:t})&=[z_1,...,z_t]K(x_{1:t},x_{1:t}) \\ K(x_i,x_{1:t})&=[\sum_{j=1}^t{z_jK(x_j,x_1)},...,\sum_{j=1}^t{z_jK(x_j,x_t)}] \\ \end{align*} \]

上述式子需對任意\(K(x,x’)\)都成立。列出方程組，得：

\[\left\{\begin{align*} \sum_{j=1}^t{z_jK(x_j,x_1)}&=K(x_i,x_1) \\ ... \\ \sum_{j=1}^t{z_jK(x_j,x_t)}&=K(x_i,x_t) \end{align*}\right. \]

由於\(K(x_{1:t},x_{1:t})\)可以求逆，因此它是滿秩的，這意味著上面的方程組一定有唯一解。

經過變換得出：

\[\left\{\begin{align*} \sum_{j\neq i}{z_jK(x_j,x_1)}&=(1-z_i)K(x_i,x_1) \\ ... \\ \sum_{j\neq i}{z_jK(x_j,x_t)}&=(1-z_i)K(x_i,x_t) \end{align*}\right. \]

由於右側的項都是一樣的，而左側\(K(x_i,x_j),j=1,...t\)各有不同，要想使他們相等，就必須等於0。因此解得：

\[\left\{\begin{align*} z_i&=1& \\ z_j&=0&, j\neq i,j=1,...t \end{align*}\right. \]

故有：對任意\(A=[a_1,...,a_t]^T\)，\(i=1,...,t\)，都有\(K(x_i,x_{1:t})K(x_{1:t},x_{1:t})^{-1}A=a_i\)。

一文詳解貝葉斯優化（Bayesian Optimization）原理