manacher演演算法
manacher演演算法
斯♥哈♥學長的部落格https://www.cnblogs.com/luckyblock/p/17044694.html#5140558
為什麼老師叫他馬拉車演演算法/yiw
簡介
我們都知道，求最長迴文子串可以列舉每一個開始的點，然後直接一個一個比較就完事，但這樣的複雜度是接近 \(O(n^{2})\) 的，不出意外你就會
，那麼我們這個時候就需要用到 manacher 演演算法了，他和 KMP 一樣都是基於暴力的思想改進的一種演演算法，利用了已求得的迴文半徑加速了比較的過程，使複雜度降到了 \(O(n)\) 級別。
過程
上面已經提到 manacher 演演算法是解決最長迴文子串的問題的。
迴文串可以分為兩種型別：一種是長度為奇數的迴文串，比如 \(12321\)，另一種是長度為偶數的迴文串，比如： \(123321\)，這個時候我們要是想分類討論的話也太麻煩了，所以我們就開始用一些奇♂技♂淫♂巧：我們在每一個串的首尾和每一個字元之間插♂入一個字串，就像下面這樣：\(!1!2!3!2!1!\)，\(!1!2!3!3!2!1!\)，這個時候能發現，這倆串都成了長度為奇數的迴文串了，那麼我們就可以不用分類討論了。
我們定義 \(p[i]\) 為以 \(i\) 為中心的迴文串的最長半徑，比如串 \(\%a\%b\%a\%\)，其中 \(b\) 為第四個字元，則 \(p[4]=4\)（因為以他為中心的最長迴文串是 \(\%a\%b\%a\%\)，而這個迴文串的半徑為 \(4\)）。所以我們在原字串中的這個迴文字串長度就是 \(p[i]-1\)，為什麼嘞？因為我們原字串中是這樣的 \(aba\)，設上面修改過的串的長度為 \(n\)，則原字串的長度為 \(\frac{n-1}{2}\)，而我們的半徑剛好是 \(\frac{n+1}{2}\)，半徑減去原字串長度則為 \(\frac{n+1-n+1}{2}\)，也就是 \(1\)，所以我們就可以知道半徑減去 \(1\)，就是原字串的長度啦。（你問我為什麼給你證這個？當然是後面的我不會證）接下來我們就要來快速求出 \(p[i]\) 陣列了，我們假設 \(pos\) 是一個已經記錄的值，R$ 為以 \(pos\) 為中心的迴文串的最長右邊界，然後現在要求 \(p[i]\)，\(j\) 是 \(i\) 關於 \(pos\) 的對稱點，也就是說 \(j=2\times pos-i\)。
這個時候就分兩種情況了，第一種情況就是 \(j\) 的迴文串沒有跳出 \(L\)，也就是這樣：
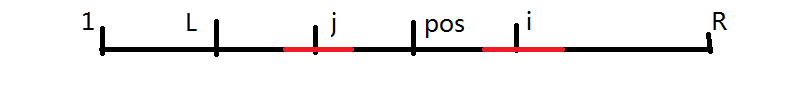
因為 \(L\) 到 \(R\) 是一個迴文串，所以 \(i\) 的迴文和 \(j\) 的迴文相同，即 \(p[i]=p[j]\).
第二種情況就是 \(j\) 的最長迴文越過了 \(L\)，也就是下面這樣：
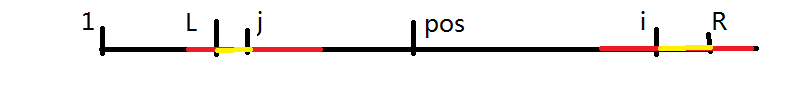
如果在這種情況下，\(j\) 的最長迴文就不一定是 \(i\) 的最長迴文了。然後黃色那塊肯定還是迴文。
所以綜上，\(p[i]=min(p[2\times pos-1],R-i)\)
如果可以的話，繼續暴力拓展即可。
複雜度不會證，看上面學長的部落格吧。
P3805 【模板】manacher 演演算法
#include<bits/stdc++.h>
#define int long long
#define N 20001000
using namespace std;
int p[N<<1],ans,cnt;
char s[N<<1];
signed main()
{
char c=getchar();
s[0]='~';s[++cnt]='%';
while(c<'a'||c>'z')c=getchar();
while(c>='a'&&c<='z')s[++cnt]=c,s[++cnt]='%',c=getchar();
int r=0,mid=0;
for(int t=1;t<=cnt;t++)
{
if(t<=r)p[t]=min(p[mid*2-t],r-t+1);//如果當前的中心是小於r的話，取兩頭的min
while(s[t-p[t]]==s[t+p[t]])++p[t];//向兩邊擴充套件
if(p[t]+t>r)r=p[t]+t-1,mid=t;//如果超界就要更新r和mid的值
ans=max(p[t],ans);//如果要是當前的半徑比答案大就替換
}
cout<<ans-1<<endl;
return 0;
}
P4555 [國家集訓隊]最長雙迴文串
開啟標籤發現有 manacher 演演算法所以開始考慮 manacher 演演算法
但是當我求出 \(p\) 陣列的時候，我沉默了，兩個的話不好找，所以考慮維護其他的東西。
既然我們是要求兩相鄰的迴文串的最大長度，那麼我們可以考慮維護一下以一個點為開始的迴文串最大長度和以一個點為結尾的迴文串最大長度，但是這就又有一個問題，就是當前點的字元是被算入了兩個串裡，考慮一下，我們在一開始插入了一些特殊字元，我們只要列舉這些特殊字元的不就好了嗎！因為後面刪去是不影響的。然後就是該如何維護，首先我們可以在求 \(p\) 的時候順手維護一部分，因為當 \(i\) 為中點時，左端點為 \(i-p[i]+1\)，右端點為 \(i+p[i]-1\)，那麼我們就可以先對這個求一個max，將其存放到 \(l\)，\(r\) 兩個陣列裡面去，但是由於求 \(p\) 的時候都是最大的，所以導致一些短的迴文串的開頭結尾的陣列沒有存入，所以我們需要再推一遍，首先 \(r\) 是要倒著列舉的，因為是逐漸向左移，然後，當前的 \(r\) 陣列有兩種選擇，一種是他的右一個字元的最大回文長度減一，因為中間插入了字元，在迴圈的時候是 \(i+=2\) 的，然後減去一也變成了減去二，下標也是 \(i+2\)，最後得出： \(r[i]=\max(r[i],r[i+2]-2)\)，\(l\) 陣列同理可推得：\(l[i]=\max(l[i],l[i-2]-2)\)。然後最後遍歷一遍所有的特殊字元對於 \(l[i]+r[i]\) 取一個 \(\max\) 就好啦！
#include<bits/stdc++.h>
#define int long long
#define N 1000100
using namespace std;
int n,p[N<<1],cnt,l[N<<1],r[N<<1],ans;
char s[N<<1];
signed main()
{
char c=getchar();
s[cnt]='~',s[++cnt]='%';
while(c<'a'||c>'z')c=getchar();
while(c>='a'&&c<='z')s[++cnt]=c,s[++cnt]='%',c=getchar();
s[cnt+1]=')';
int j=0,mid=0;
for(int i=1;i<=cnt;i++)
{
if(i<=j)p[i]=min(p[2*mid-i],j-i+1);
while(s[i-p[i]]==s[i+p[i]])p[i]++;
if(p[i]+i>j)j=p[i]+i-1,mid=i;
l[i-p[i]+1]=max(l[i-p[i]+1],p[i]-1);
r[i+p[i]-1]=max(r[i+p[i]-1],p[i]-1);
}
// cout<<"cao"<<endl;
for(int i=cnt;i>=1;i-=2)r[i]=max(r[i],r[i+2]-2);
for(int i=1;i<=cnt;i+=2)l[i]=max(l[i],l[i-2]-2);
for(int i=1;i<=cnt;i+=2)if(l[i]&&r[i])ans=max(l[i]+r[i],ans);
cout<<ans<<endl;
return 0;
}
P1659 [國家集訓隊]拉拉隊排練
既然是求解迴文串的問題，首先可以考慮一下 manacher 演演算法。
我發現題解中有的是直接在原串上跑 manacher，這樣可以直接過濾掉長度為偶數的迴文串，如果是要在修改後的串上跑 manacher 的話，我們在統計答案的時候可以直接特判一下，把是以原串裡的字元為中心的迴文串最大長度給算上，這樣在原串裡也是長度為奇數的迴文串了。
對於排序的問題，我們可以開一個桶 \(t\) 陣列來記錄一下當前長度的迴文串的數量，很容易發現，我們的 \(p[i]\) 裡面存放的是以 \(i\) 為中心最大的迴文半徑，所以我們知道，像 \(abcdedcba\) 這種迴文串，不僅只有這一個最長的，當去掉兩頭各一個字元時，就可以得到了另一個迴文串 \(bcdedcb\)。
現在考慮如果處理以上的情況。如果是在往桶裡面存放的時候用一個迴圈來一直減二修改的話，像一些以當前點為迴文中心的字串很長的情況就會 T 掉了，所以我們要用到類似於線段樹的懶標記的方法，我們在將當前的迴文串長度也就是 \(p[i]-1\) 放入桶中的時候，先不要急著給後面的也放入，等到了查詢的時候，當前的 \(t[p[i]-1]\) 計算完了以後，我們再給 \(t[p[i]-1-2]\) 加上 \(t[p[i]-1]\) 的值，就相當於長度為 \(p[i]-1\) 的迴文串全都去掉了兩頭各一個字元，變為了 長度為 \(p[i]-1-2\) 的迴文串，這樣可以使我們的複雜度大大降低，跑的也很快。
\(k\) 的範圍較大，要用快速冪，同時注意取模和判無解。
#include<bits/stdc++.h>
#define int long long
#define P 19930726
#define N 1000010
using namespace std;
int n,k,p[N<<1],t[N<<1],cnt,maxn;
char s[N<<1];
inline int ksm(int x,int y)
{
int sum=1;
while(y)
{
if(y%2==1)
sum=(sum*x)%P;
x=(x*x)%P;
y=y>>1;
}
return sum%P;
}
signed main()
{
cin>>n>>k;
char c=getchar();
s[cnt]='!';s[++cnt]='%';
while(c<'a'||c>'z')c=getchar();
while(c>='a'&&c<='z')s[++cnt]=c,s[++cnt]='%',c=getchar();
s[cnt+1]='~';
int j=0,mid=0;
for(int i=1;i<=cnt;i++)
{
if(i<=j)p[i]=min(p[2*mid-i],j-i+1);
while(s[i+p[i]]==s[i-p[i]])p[i]++;
if(p[i]+i>j)j=p[i]+i-1,mid=i;
if(s[i]!='%')
{
int xx=p[i]-1;
t[xx]++;
maxn=max(maxn,p[i]-1);
}
}
// for(int i=1;i<=maxn;i++)
// cout<<t[i]<<" ";
// cout<<endl;
int ans=1,sum=0;
for(int i=maxn;i>=1;i--)
{
if(sum+t[i]>k)
{
ans=(ans*ksm(i,k-sum)%P);
sum+=t[i];
break;
}
sum+=t[i];
t[i-2]+=t[i];
ans=(ans*ksm(i,t[i])%P);
}
if(sum<k)
{
cout<<"-1"<<endl;
return 0;
}
cout<<ans<<endl;
return 0;
}
P9606 [CERC2019] ABB
不難發現最壞情況就是把前 \(n-1\) 個字元反轉一下複製到後面。
發現字尾的迴文串長度會使得新增的字元個數減少，例如樣例三中 murderforajarof 實際上最後是在後面複製了 redrum，也就是說我們找到一個最右端為 \(n\) 的最長迴文串，\(n\) 減去這個串的長度即為最優方案。
考慮如何計算。
求最大回文想到 manacher 演演算法，發現求出 \(p\) 陣列後，若當前的右端點為最後一個字元的位置就可以計算，也就是當 \(p_i + i - 1 =m\) 時，答案為 \(n - p_i + 1\)。
/*
* @Author: Aisaka_Taiga
* @Date: 2023-10-23 15:12:00
* @LastEditTime: 2023-10-23 16:08:55
* @LastEditors: Aisaka_Taiga
* @FilePath: \Desktop\P9606.cpp
* The heart is higher than the sky, and life is thinner than paper.
*/
#include <bits/stdc++.h>
#define int long long
#define N 1000100
using namespace std;
int n, ans, p[N], m;
char s[N], ss[N];
signed main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> ss[i];
s[0] = '~', s[++ m] = '%';
for(int i = 1; i <= n; i ++)
{
s[++ m] = ss[i];
s[++ m] = '%';
}
int r = 0, mid = 0;
for(int i = 1; i <= m; i ++)
{
if(i <= r) p[i] = min(p[2 * mid - i], r - i + 1);
while(s[i + p[i]] == s[i - p[i]]) p[i] ++;
if(p[i] + i > r) r = p[i] + i - 1, mid = i;
}
ans = n - 1;
// for(int i = 1; i <= m; i ++) if(s[i] != '%') cout << (p[i] / 2) << " "; cout << endl;
for(int i = 1; i <= m; i ++)
if(p[i] + i - 1 == m)
ans = min(ans, n - p[i] + 1);
cout << ans << endl;
return 0;
}
本文來自部落格園，作者：Aisaka_Taiga，轉載請註明原文連結：https://www.cnblogs.com/Multitree/p/17069324.html
The heart is higher than the sky, and life is thinner than paper.