【演演算法】萬聖節前夕的迷宮挑戰(二)
在十月底一個陽光明媚的週末,小悅開始她的徒步旅行,一頭高高的馬尾輕輕搖曳,充滿了青春的活力。她的笑容如同春日的陽光,溫暖而明亮,總是讓人心情愉悅。那天的徒步旅行,她選擇了一條山區路線,期望能欣賞到秋天那五彩斑斕的樹葉和感受大自然的魅力。
旅途中,小悅遇到了一些意料之外的障礙。她發現自己的體力迅速流失,山路比她想象的要陡峭得多。每走一步,她都需要調整自己的步伐和呼吸,以更好地應對挑戰。面對這些困難,她知道,除了身體的鍛鍊,還有心態的調整。為了繼續前行,她需要保持積極樂觀的態度。
小悅繼續她的徒步旅行,欣賞著秋天的美景,同時也感受到了自己的成長和進步。回想起上週解決的迷宮障礙演演算法,她意識到這次的山區迷宮有一個重要的不同之處——體力的因素。山區迷宮不僅有曲折的小道和死衚衕,還有陡峭的山坡和崎嶇的山路。為了成功找到出路,小悅需要考慮自己的體力和耐力。她需要找到一條既能避開障礙物,又能最大限度地節省體力的路徑。
於是,小悅開始仔細觀察山區迷宮的地形和環境。她發現有些路徑雖然看似直接,但是卻需要爬過一個個陡峭的山坡,消耗大量體力。而有些路徑雖然繞遠了一些,但是卻相對平緩,更加節省體力。為了成功找到出路並節省體力,小悅權衡利弊,選擇了一條既能躲避障礙,又能最大限度地節省體力的路徑。
她開始運用在徒步旅行中學到的技巧和知識,結合上星期解決迷宮的演演算法,尋找最佳路徑。通過不斷嘗試和調整,她成功地避開了陡峭的山坡,選擇相對平緩的山路。雖然這樣的選擇可能會繞遠一些,但她相信這是最明智的決策。
在山區迷宮中艱難前行時,小悅感到體力不支,但她堅持下去。她知道只有克服體力的挑戰,才能找到正確的出路。隨著時間的推移,小悅的身體逐漸適應了徒步旅行的挑戰。她的肌肉變得更加結實,體力也得到了提升。她的健美身材和流暢的步伐吸引了路人的目光。
最終,小悅成功地走出了山區迷宮。她感到一種前所未有的成就感和滿足感。這次徒步旅行不僅是一次身體上的挑戰,更是一次心理上和體力上的雙重考驗。通過這次旅行,小悅學會了在困難和挑戰面前綜合考慮各種因素做出明智的決策。
小悅在徒步時面臨的問題是:她在二維陣列NxN山區的起始位置[0,0],只能在四個主要方向之一(即北、東、南、西)移動。需要移動到目標位置[N-1,N-1],計算出最小的爬山量(體力)。相鄰位置之間的爬山量(體力)定義為位置高度差(上升2或下降2)。
位置海拔高度定義為一個整數(0-9),代表上山和下山需要的體力。
圖解:
演演算法實現1:
1 public static int PathFinder(string maze) 2 { 3 var M = maze.Replace("\n", "").Select(c => (int)c).ToArray(); // 將迷宮字串轉換為整數陣列 4 var N = (int)Math.Sqrt(M.Length); // 迷宮的維度 5 var C = new int[M.Length]; // 每個節點的移動成本 6 7 Array.Fill(C, int.MaxValue, 1, M.Length - 1); 8 9 var Q = new List<int> { 0 }; // 定義佇列 10 11 while (Q[0] != M.Length - 1) // 當佇列Q的第一個節點不是終點時,繼續迴圈 12 { 13 var index = Q.First(); // 取出佇列Q的第一個節點 14 Q.RemoveAt(0); // 將佇列Q的第一個節點移除 15 16 foreach (var n in Neighbours(index, M, N)) // 遍歷當前節點的鄰居節點 17 { 18 int nc = C[index] + Math.Abs(M[n] - M[index]); // 計算從當前節點到鄰居節點的新的移動成本 19 if (C[n] > nc) // 如果鄰居節點的當前移動成本大於新的移動成本 20 { 21 C[n] = nc; // 更新鄰居節點的移動成本 22 Insert(Q, C, n); // 將鄰居節點插入到佇列Q中 23 } 24 } 25 } 26 27 return C[Q[0]]; 28 } 29 30 static void Insert(List<int> Q, int[] C, int index) 31 { 32 for (int i = 0; i < Q.Count; i++) // 遍歷佇列Q中的節點 33 { 34 if (C[Q[i]] > C[index]) // 如果當前節點的移動成本小於佇列Q中的某個節點的移動成本 35 { 36 Q.Insert(i, index); // 將當前節點插入到佇列Q中 37 return; 38 } 39 } 40 Q.Add(index); // 如果當前節點的移動成本大於佇列Q中的所有節點的移動成本,將當前節點新增到佇列Q的末尾 41 } 42 43 static List<int> Neighbours(int index, int[] M, int N) 44 { 45 var neighbours = new List<int>(); 46 47 if (index % N != 0) neighbours.Add(index - 1); // 左邊的鄰居 48 if (index % N != N - 1) neighbours.Add(index + 1); // 右邊的鄰居 49 if (index + N < M.Length) neighbours.Add(index + N); // 下面的鄰居 50 if (index - N >= 0) neighbours.Add(index - N); // 上面的鄰居 51 52 return neighbours; 53 }
這個演演算法是一個基於Dijkstra演演算法的尋路演演算法,Dijkstra演演算法是由荷蘭電腦科學家艾茲格·迪傑斯特拉在1956年提出的,因此又叫迪傑斯特拉演演算法。該演演算法是從一個頂點到其餘各頂點的最短路徑演演算法,解決的是有權圖中最短路徑問題。它的核心思想是利用優先佇列來實現最短路徑的搜尋,同時通過引入啟發式函數來加速搜尋過程。在這個演演算法中,每個節點的權重是從起點到該節點的移動成本,而啟發式函數則是從該節點到終點的估計成本。通過不斷更新每個節點的移動成本和啟發式函數,演演算法能夠找到從起點到終點的最短路徑。這個演演算法的優點是可以處理任意形狀的迷宮,並且具有較好的時間複雜度。
通過測試用例解釋這個基於Dijkstra演演算法的尋路演演算法:
var b = "010\n" +
"010\n" +
"010",
var c = "010\n" +
"101\n" +
"010",
Assert.AreEqual(2, Finder.PathFinder(b));
Assert.AreEqual(4, Finder.PathFinder(c));
基於Dijkstra演演算法的尋路演演算法是一種用於在加權圖中找到節點之間最短路徑的演演算法。它通過迭代計算每個節點的距離,從起點節點開始,直到到達終點節點。下面使用測試用例來解釋這個演演算法的工作原理。
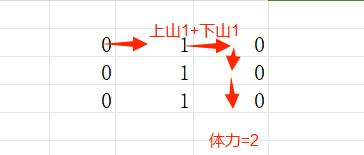
對於迷宮地圖b,它的結構如下:
010 010 010 我們要找到從起點到終點的最短路徑。根據Dijkstra演演算法的步驟,我們首先將起點節點標記為距離為0,然後計算與起點相鄰的節點的距離。在這個例子中,起點節點是(0,0),它相鄰的節點是(1,0)和(0,1)。我們計算這些節點的距離,並選擇距離最短的節點(1,0)作為下一個存取節點。然後,我們繼續計算與(1,0)相鄰的節點的距離,選擇距離最短的節點作為下一個存取節點。以此類推,直到到達終點節點(2,2)。在這個過程中,我們記錄下每個節點的距離,並選擇最短路徑。
對於迷宮地圖b,最短路徑為: (0,0) -> (1,0) -> (2,0) -> (2,1) -> (2,2)
這條路徑的爬坡體力為2。
對於迷宮地圖c,它的結構如下:
010 101 010 同樣地,我們要找到從起點到終點的最短路徑。根據Dijkstra演演算法的步驟,我們首先將起點節點標記為距離為0,然後計算與起點相鄰的節點的距離。在這個例子中,起點節點是(0,0),它相鄰的節點是(1,0)和(0,1)。我們計算這些節點的距離,並選擇距離最短的節點(1,0)作為下一個存取節點。然後,我們繼續計算與(1,0)相鄰的節點的距離,選擇距離最短的節點作為下一個存取節點。以此類推,直到到達終點節點(2,2)。在這個過程中,我們記錄下每個節點的距離,並選擇最短路徑。
對於迷宮地圖c,最短路徑為: (0,0) -> (1,0) -> (1,1) -> (2,1) -> (2,2)
這條路徑的爬坡體力為4。
因此,基於Dijkstra演演算法的尋路演演算法能夠找到從起點到終點的最短路徑,並返回路徑的爬坡體力。
注:演演算法1中並沒有直接計算體力花費,而是根據題目給定的規則,將體力花費轉化為了路徑的代價。在這個演演算法中,代價的計算方式是通過累加每個節點之間的高度差來計算的。
具體來說,這個演演算法中的代價(C陣列)表示從起點到每個節點的路徑代價,也就是到達該節點需要的體力花費。在每次更新路徑代價時,會根據當前節點和鄰居節點的高度差來計算新的代價。這裡使用了Math.Abs方法來計算高度差的絕對值,然後將其累加到路徑代價中。
在演演算法的主迴圈中,通過遍歷起點的鄰居節點,計算新的路徑代價,並將其與原來的路徑代價進行比較。如果新的路徑代價更小,則更新路徑代價並將鄰居節點插入到佇列中。這樣,演演算法會不斷更新路徑代價,直到找到終點或佇列為空。
演演算法實現2:
1 public static int PathFinder(string maze) 2 { 3 // 將迷宮字串按行分割,並將每個字元轉換為數位,儲存在一個二維陣列中 4 var m = maze.Split('\n').Select(s => s.Select(c => int.Parse("" + c)).ToArray()).ToArray(); 5 var n = m.Length; 6 var points = new Point[n, n]; // 建立一個二維陣列,儲存每個點的位置、啟發值和移動距離 7 int i, j; 8 var neighbors = new List<Point>(); // 建立一個列表,儲存當前點的相鄰點 9 10 // 初始化每個點的位置和啟發值 11 for (i = 0; i < n; ++i) 12 for (j = 0; j < n; ++j) 13 points[i, j] = new Point { I = i, J = j, Heuristic = (n - i) + (n - j) }; 14 15 var heap = new BinaryHeap<Point>(); // 建立一個二元堆積,用於儲存和管理點物件 16 points[0, 0].Moves = 0; // 設定起點的移動距離為0 17 heap.Add(points[0, 0]); // 將起點加入二元堆積中 18 19 while (heap.Count != 0) 20 { 21 var here = heap.Remove(); // 取出二元堆積中的最小值,即當前離起點最近的點 22 i = here.I; 23 j = here.J; 24 25 if (i == n - 1 && j == n - 1) // 如果當前點為終點,返回從起點到該點的移動距離 26 return here.Moves; 27 28 neighbors.Clear(); // 清空相鄰點列表 29 // 找出當前點的四個相鄰點,並加入相鄰點列表 30 if (i + 1 < n) neighbors.Add(points[i + 1, j]); 31 if (j + 1 < n) neighbors.Add(points[i, j + 1]); 32 if (i - 1 >= 0) neighbors.Add(points[i - 1, j]); 33 if (j - 1 >= 0) neighbors.Add(points[i, j - 1]); 34 35 // 遍歷相鄰點列表 36 foreach (var neighbor in neighbors) 37 { 38 // 計算從當前點到相鄰點的移動距離 39 var moves = here.Moves + Math.Abs(m[i][j] - m[neighbor.I][neighbor.J]); 40 41 if (moves < neighbor.Moves) // 如果新的移動距離小於相鄰點的移動距離 42 { 43 neighbor.Moves = moves; // 更新相鄰點的移動距離 44 neighbor.Score = moves + neighbor.Heuristic; // 更新相鄰點的得分 45 heap.AddOrUpdate(neighbor); // 將相鄰點加入或更新到二元堆積中 46 } 47 } 48 } 49 50 return -1; // 如果迴圈結束仍未找到終點,則返回-1 51 } 52 53 public class Point : IComparable<Point> 54 { 55 public int I { get; set; } 56 public int J { get; set; } 57 public int Score { get; set; } = int.MaxValue; 58 public int Moves { get; set; } = int.MaxValue; 59 public int Heuristic { get; set; } 60 61 public int CompareTo(Point other) 62 { 63 return Score.CompareTo(other.Score); 64 } 65 } 66 67 public class BinaryHeap<T> where T : IComparable<T> 68 { 69 private List<T> _heap = new List<T>(); // 儲存堆中的元素 70 private Dictionary<T, int> _items = new Dictionary<T, int>(); // 儲存元素在堆中的索引 71 72 public int Count => _heap.Count; // 堆中元素的個數 73 74 public bool Contains(T item) => _items.ContainsKey(item); // 判斷堆中是否包含指定元素 75 76 public void Add(T item) // 向堆中新增元素 77 { 78 if (Contains(item)) throw new Exception("Item already added."); // 如果堆中已經包含該元素,則丟擲異常 79 _heap.Add(item); // 將元素新增到堆中 80 UpdateIndices(Count - 1); // 更新元素在堆中的索引 81 BubbleUp(_heap.Count - 1); // 將新新增的元素進行上浮操作 82 } 83 84 public T Peek() => _heap.FirstOrDefault(); // 獲取堆頂元素 85 86 public T Remove() // 移除並返回堆頂元素 87 { 88 if (_heap.Count == 0) return default(T); // 如果堆為空,則返回預設值 89 var top = _heap.First(); // 獲取堆頂元素 90 var last = _heap.Last(); // 獲取堆中最後一個元素 91 _heap.RemoveAt(_heap.Count - 1); // 移除堆中最後一個元素 92 _items.Remove(top); // 移除堆頂元素在索引字典中的記錄 93 if (_heap.Count == 0) 94 return top; 95 _heap[0] = last; // 將最後一個元素放到堆頂 96 BubbleDown(0); // 將堆頂元素進行下沉操作 97 return top; 98 } 99 100 public void AddOrUpdate(T item) // 新增或更新元素 101 { 102 if (_items.ContainsKey(item)) // 如果元素已經存在於堆中 103 { 104 BubbleUp(_items[item]); // 進行上浮操作 105 BubbleDown(_items[item]); // 進行下沉操作 106 } 107 else Add(item); // 否則,將元素新增到堆中 108 } 109 110 private void BubbleUp(int index) // 上浮操作 111 { 112 var i = index; 113 var p = (i - 1) / 2; // 計算父節點索引 114 while (i > 0 && i < _heap.Count && _heap[i].CompareTo(_heap[p]) < 0) // 當前節點小於父節點時進行交換 115 { 116 Swap(i, p); // 交換當前節點和父節點 117 i = p; // 更新當前節點索引為父節點索引 118 p = (i - 1) / 2; // 更新父節點索引 119 } 120 } 121 122 private void BubbleDown(int index) // 下沉操作 123 { 124 int i = index; 125 int c = i * 2 + 1; // 計算左子節點索引 126 bool swapped = true; 127 while (c < _heap.Count && swapped) // 當左子節點存在且發生交換時繼續下沉 128 { 129 if (c + 1 < _heap.Count && _heap[c + 1].CompareTo(_heap[c]) < 0) // 如果右子節點存在且小於左子節點 130 ++c; // 更新子節點索引為右子節點索引 131 if (_heap[i].CompareTo(_heap[c]) > 0) // 當前節點大於子節點時進行交換 132 { 133 Swap(i, c); // 交換當前節點和子節點 134 i = c; // 更新當前節點索引為子節點索引 135 c = i * 2 + 1; // 更新子節點索引 136 } 137 else swapped = false; // 如果當前節點小於等於子節點,則停止下沉 138 } 139 } 140 141 private void Swap(int i, int j) // 交換元素位置 142 { 143 var t = _heap[i]; 144 _heap[i] = _heap[j]; 145 _heap[j] = t; 146 UpdateIndices(i, j); // 更新交換後元素的索引 147 } 148 149 private void UpdateIndices(params int[] indices) // 更新元素在索引字典中的記錄 150 { 151 foreach (var i in indices) 152 { 153 _items[_heap[i]] = i; 154 } 155 } 156 }
演演算法2中的PathFinder方法使用了A*演演算法來解決這個問題。
A*演演算法是一種經典的啟發式搜尋演演算法,用於解決圖搜尋問題。它由Peter Hart、Nils Nilsson和Bertram Raphael於1968年提出,並在1972年由Peter Hart、Nils Nilsson和Bertram Raphael發表了一篇論文。
A*演演算法的產生原因是為了解決傳統的圖搜尋演演算法在搜尋空間較大時效率低下的問題。傳統的圖搜尋演演算法,如深度優先搜尋和廣度優先搜尋,會遍歷所有可能的路徑,直到找到目標節點。這種方法在搜尋空間較大時,會浪費大量時間和計算資源。
A*演演算法通過引入啟發式函數來優化搜尋過程。啟發式函數是一種估計從當前節點到目標節點的代價的函數。A*演演算法使用啟發式函數來選擇下一步移動的方向,以儘可能快地接近目標節點。
A*演演算法的核心思想是維護一個優先佇列(通常使用二元堆積實現),按照啟發式函數的值對節點進行排序。在每一步中,選擇優先佇列中具有最小啟發式函數值的節點作為當前節點,然後將其周圍的節點加入優先佇列。通過不斷選擇具有最小啟發式函數值的節點,A演演算法可以在較短的時間內找到從起點到目標節點的最短路徑。
A**演演算法在解決各種圖搜尋問題中表現出色,並且已經被廣泛應用於路徑規劃、遊戲AI、人工智慧等領域。它的優勢在於能夠在較短的時間內找到最優解,並且可以通過調整啟發式函數來適應不同的問題和需求。
對比演演算法1和演演算法2,Dijkstra演演算法和A*演演算法都是用於解決圖搜尋問題的演演算法,但它們在搜尋策略和效率上有一些區別。
- 搜尋策略:
-
- Dijkstra演演算法是一種無資訊搜尋演演算法,它會遍歷所有可能的路徑,直到找到目標節點。它將圖中的節點按照距離起點的距離進行排序,並選擇距離最小的節點作為當前節點進行擴充套件。這種搜尋策略確保找到的路徑是最短路徑,但可能會遍歷大量的無關節點。
- A*演演算法是一種啟發式搜尋演演算法,它使用啟發式函數來估計從當前節點到目標節點的代價。它根據啟發式函數的值對節點進行排序,並選擇具有最小啟發式函數值的節點進行擴充套件。這種搜尋策略可以幫助演演算法更快地接近目標節點,避免遍歷大量無關節點。
- 效率:
-
- Dijkstra演演算法在最壞情況下的時間複雜度為O(|V|^2),其中|V|是圖中節點的數量。它需要遍歷所有節點,並在每一步中選擇距離起點最近的節點進行擴充套件。這使得Dijkstra演演算法在處理大規模圖時效率較低。
- A演演算法在最壞情況下的時間複雜度為O(|E|),其中|E|是圖中邊的數量。它通過使用啟發式函數來指導搜尋,可以更快地找到最短路徑。但是,A演演算法的效率高度依賴於啟發式函數的質量。如果啟發式函數不準確或不合理,A*演演算法可能會走彎路或陷入區域性最優解
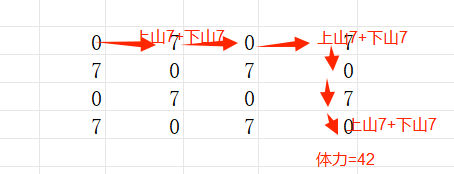
- 最短路徑:
-
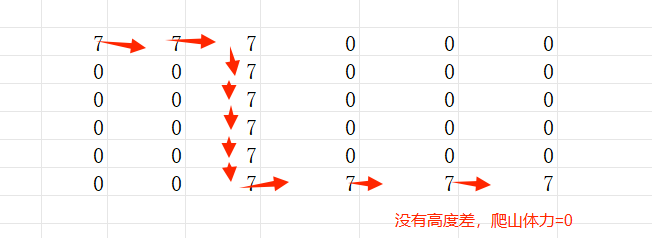
- Dijkstra演演算法保證找到的路徑是最短路徑,因為它遍歷所有可能的路徑並選擇距離起點最近的節點進行擴充套件。這使得Dijkstra演演算法在尋找最短路徑方面非常可靠。
- A演演算法在啟發式函數合理的情況下,也可以找到最短路徑。啟發式函數可以提供對目標節點的估計,幫助演演算法更快地接近目標節點。但是,如果啟發式函數不準確或不合理,A演演算法可能會找到次優解或不完全最短路徑。
- 走過路徑的體力花費:
-
- Dijkstra演演算法沒有考慮任何體力花費因素,它只關注路徑的距離,如果需要計算體力花費,需要額外寫路徑代價的轉化邏輯。因此,Dijkstra演演算法不能直接優化體力花費,而是隻找到最短路徑。
- A演演算法可以通過合理選擇啟發式函數來考慮體力花費因素。啟發式函數可以估計從當前節點到目標節點的體力花費,並在搜尋過程中優先選擇體力花費較低的節點。這使得A演演算法在考慮體力花費時更具優勢。
綜上所述,Dijkstra演演算法適用於需要找到最短路徑的問題,並且對搜尋空間的規模沒有太高的要求。A*演演算法適用於大規模圖搜尋問題,並且可以通過合理選擇啟發式函數來提高搜尋效率。在實際應用中,需要根據具體問題的特點和需求選擇適合的演演算法。如果只關注最短路徑,Dijkstra演演算法是一個可靠的選擇。如果需要考慮體力花費,並且可以設計合理的啟發式函數,A*演演算法可以更好地優化路徑選擇。然而,在實際應用中,需要根據具體問題的需求和約束來選擇適合的演演算法。
對比一週前的迷宮躲避障礙演演算法,在地圖導航應用場景中,這四個演演算法(BFS、Dijkstra、A*和洪水遞迴演演算法)有以下區別:
-
廣度優先搜尋(BFS):BFS適用於無權圖或迷宮中尋找最短路徑。它能夠找到最短路徑,但沒有考慮權重或啟發式函數。BFS的時間複雜度為O(V+E),其中V是頂點數,E是邊數。
-
Dijkstra演演算法:Dijkstra演演算法適用於帶有非負權重的圖中尋找最短路徑。它能夠找到最短路徑,並考慮了權重。Dijkstra演演算法的時間複雜度為O((V+E)logV)。Dijkstra演演算法適用於以下情況:
- 地圖中存在不同的道路或路徑有不同的權重,比如某些道路有交通擁堵或者有收費(高速公路)。
- 需要找到最短路徑而不僅僅是一條路徑。
-
A演演算法:A演演算法適用於帶有啟發式函數的圖中尋找近似最短路徑。它通過啟發式函數來估計節點到終點的距離,並根據估計距離選擇下一個要探索的節點。A演演算法的時間複雜度取決於啟發式函數的準確性。A演演算法適用於以下情況:
- 地圖中存在不同的道路或路徑有不同的權重,比如某些道路有交通擁堵或者有收費(高速公路)。
- 地圖中存在啟發式函數可以提供對節點到終點距離的良好估計。
- 需要找到近似最短路徑,並且啟發式函數能夠提供較好的效能。
-
洪水遞迴演演算法:洪水遞迴演演算法是一種簡單的遞迴演演算法,它通過遞迴填充來更新每個位置的最小步數。洪水遞迴演演算法沒有顯式的啟發式函數,只能找到從起點到終點的一條路徑,但不一定是最短路徑。洪水遞迴演演算法適用於以下情況:
- 只需要找到一條路徑,而不需要最短路徑。
- 地圖中沒有權重或者權重對結果影響不大。
除了地圖導航,這四個演演算法(BFS、Dijkstra、A*和洪水遞迴演演算法)還有其他應用場景,例如:
-
BFS演演算法可以用於社群網路中的好友關係查詢、迷宮遊戲中的路徑搜尋、廣告投放中的目標受眾搜尋等。
-
Dijkstra演演算法可以用於路由演演算法中的最短路徑查詢、電力系統中的電網最佳化設計、通訊網路中的資料傳輸優化等。
-
A*演演算法可以用於遊戲AI中的路徑規劃、機器人導航中的路徑規劃、自動駕駛中的路徑規劃等。
-
洪水遞迴演演算法可以用於影象處理中的區域填充、計算機視覺中的影象分割、自然語言處理中的詞性標註等。
綜上所述,這四個演演算法在許多領域都有廣泛的應用,可以用於解決許多最短路徑或路徑規劃問題。
測試用例:
1 using NUnit.Framework; 2 using System; 3 using System.Collections.Generic; 4 using System.Drawing; 5 using System.Linq; 6 public class SolutionTest 7 { 8 [Test] 9 public void SampleTests() 10 { 11 12 string a = "000\n" + 13 "000\n" + 14 "000", 15 16 b = "010\n" + 17 "010\n" + 18 "010", 19 20 c = "010\n" + 21 "101\n" + 22 "010", 23 24 d = "0707\n" + 25 "7070\n" + 26 "0707\n" + 27 "7070", 28 29 e = "700000\n" + 30 "077770\n" + 31 "077770\n" + 32 "077770\n" + 33 "077770\n" + 34 "000007", 35 36 f = "777000\n" + 37 "007000\n" + 38 "007000\n" + 39 "007000\n" + 40 "007000\n" + 41 "007777", 42 43 g = "000000\n" + 44 "000000\n" + 45 "000000\n" + 46 "000010\n" + 47 "000109\n" + 48 "001010"; 49 50 Assert.AreEqual(0, Finder.PathFinder(a)); 51 Assert.AreEqual(2, Finder.PathFinder(b)); 52 Assert.AreEqual(4, Finder.PathFinder(c)); 53 Assert.AreEqual(42, Finder.PathFinder(d)); 54 Assert.AreEqual(14, Finder.PathFinder(e)); 55 Assert.AreEqual(0, Finder.PathFinder(f)); 56 Assert.AreEqual(4, Finder.PathFinder(g)); 57 } 58 59 [Test] 60 public void RandomTests() 61 { 62 63 for (int nTimes = 0; nTimes < 6; nTimes++) 64 { 65 for (int n = 1; n < 101; n++) 66 { 67 var maze = GenerateMaze(n); 68 Assert.AreEqual(RefFinder.PathFinder(maze), Finder.PathFinder(maze)); 69 } 70 } 71 } 72 73 private Random rand = new Random(); 74 75 private string GenerateMaze(int n) 76 { 77 return string.Join("\n", Enumerable.Range(0, n).Select(x => string.Concat(Enumerable.Range(0, n).Select(v => $"{rand.Next(10)}")))); 78 } 79 80 private class RefFinder 81 { 82 private static List<Point> MOVES = new List<Point> { new Point(1, 0), new Point(0, 1), new Point(0, -1), new Point(-1, 0) }; 83 84 public static int PathFinder(string maze) 85 { 86 var aMazed = maze.Split("\n").Select(s => s.Select(i => i - 48).ToArray()).ToArray(); 87 int X = aMazed.Length - 1, Y = aMazed[0].Length - 1; 88 Point pos = new Point(0, 0), end = new Point(X, Y); 89 var q = new PriorityQueue<Tup>(); 90 q.Push(new Tup(0, pos.Equals(end), pos)); 91 var seen = new Dictionary<Point, int>() { [pos] = 0 }; 92 while (!end.Equals(q.Peek().Pos)) 93 { 94 var curr = q.Pop(); 95 foreach (var move in MOVES) 96 { 97 var x = curr.Pos.X + move.X; 98 var y = curr.Pos.Y + move.Y; 99 if (x >= 0 && x <= X && y >= 0 && y <= Y) 100 { 101 var p = new Point(x, y); 102 int nextCost = curr.Cost + Math.Abs(aMazed[curr.Pos.X][curr.Pos.Y] - aMazed[p.X][p.Y]); 103 var r = seen.TryGetValue(p, out var o); 104 if (!r) 105 { 106 seen.Add(p, nextCost); 107 q.Push(new Tup(nextCost, end.Equals(p), p)); 108 } 109 else if (o > nextCost) 110 { 111 seen[p] = nextCost; 112 q.Push(new Tup(nextCost, end.Equals(p), p)); 113 } 114 } 115 } 116 } 117 return q.Peek().Cost; 118 } 119 120 /* ****************** 121 HELPER CLASS 122 ******************/ 123 124 private class Tup : IComparable<Tup> 125 { 126 public int Cost { get; } 127 public bool IsEnd { get; } 128 public Point Pos { get; } 129 130 public Tup(int cost, bool isEnd, Point pos) 131 { 132 this.Pos = pos; 133 this.Cost = cost; 134 this.IsEnd = isEnd; 135 } 136 137 public override bool Equals(object obj) 138 { 139 if (obj == null || !(obj is Tup)) return false; 140 var that = obj as Tup; 141 return Cost == that.Cost && IsEnd == that.IsEnd && Pos == that.Pos; 142 } 143 144 public override string ToString() { return $"Tup({Cost}, {(IsEnd ? 1 : 0)}, ({Pos.X},{Pos.Y}))"; } 145 146 public int CompareTo(Tup other) 147 { 148 return -(Cost != other.Cost ? Cost - other.Cost 149 : IsEnd != other.IsEnd ? (IsEnd ? 1 : 0) - (other.IsEnd ? 1 : 0) 150 : Pos.X != other.Pos.X ? Pos.X - other.Pos.X 151 : Pos.Y - other.Pos.Y); 152 } 153 } 154 } 155 }