二元樹(Binary Tree)

二元樹（Binary Tree）是一種樹形資料結構，由節點構成，每個節點最多有兩個子節點：一個左子節點和一個右子節點。

	public class TreeNode {
      	 int val;
      	 TreeNode left;
      	 TreeNode right;
      	 TreeNode(int val) { this.val = val; }
    }

基本概念

"二元樹"（Binary Tree）這個名稱的由來是因為二元樹的每個節點最多有兩個子節點，一個左子節點和一個右子節點。其中，「二叉」指的是兩個，因此「二元樹」表示每個節點最多可以分支成兩個子節點。基本定義：

每個節點包含一個值（或資料），另外最多有兩個子節點。
左子節點和右子節點的順序是固定的，左邊的子節點是左子節點，右邊的子節點是右子節點。
一個節點可以沒有子節點（葉節點），也可以有一個子節點或兩個子節點（內部節點）。

相關基本概念：

根節點（Root）：二元樹的頂部節點稱為根節點，是樹的起始點。
節點（Node）：二元樹的基本構建單元。每個節點包含一個值（或資料）以及指向左子節點和右子節點的指標。
父節點（Parent Node）：一個節點的直接上級節點，如果存在的話。例如，一個節點的左子節點的父節點是該節點本身。
葉節點（Leaf Node）： 沒有子節點的節點稱為葉節點，即左子節點和右子節點都為空。
子樹（Subtree）：以某個節點為根的樹，它包括該節點及其所有後代節點。
高度（Height）：從某個節點到其最遠葉節點的最長路徑上的邊數，也稱為節點的層數。葉節點的高度為0。

在二元樹基本定義上，加上一些規則，可以衍生出更多種類的二元樹。比如：

二元搜尋樹（Binary Search Tree，BST）：一種特殊的二元樹，滿足以下性質：對於樹中的每個節點，其左子樹中的值都小於該節點的值，而其右子樹中的值都大於該節點的值。BST通常用於實現有序資料集合。

完全二元樹（Complete Binary Tree）：一個二元樹，其所有層次（深度）除了最後一層外，都是完全填充的，且最後一層的節點從左到右填充，沒有空隙。

平衡二元樹（Balanced Binary Tree）：一種高度平衡的二元樹，其中每個節點的兩棵子樹的高度差不超過1。平衡二元樹通常用於提高查詢、插入和刪除操作的效能。

預備基礎演演算法 —— 遞迴（Recursion）

下一部分要寫的是二元樹基本遍歷程式碼實現其實可以有多種，思量後用遞迴實現應該是初接觸者比較簡潔好理解的方式。為此，在寫二元樹下一部分內容之前簡單寫下基礎遞迴演演算法，以保證本系列文章承前啟後。

遞迴(Recursion),在數學與電腦科學中對其描述的說法有很多，比如：

指在函數的定義中使用函數自身的方法；
指一種通過重複將問題分解為同類的子問題而解決問題的方法；
（PS：這裡同類子問題對於於上一種說法就是函數自身）
指由一種（或多種）簡單的基本情況定義的一類物件或方法，並規定其他所有情況都能被還原為其基本情況。
（PS：這裡描述的基本情況對應於第一種說法中的函數自身了）

當然本文非學術著作"哪種描述比較合適"在此不多做分析，從編碼實踐的角度第一種說法更為地氣一點。

「將問題分解為同類的子問題」這一點是用遞迴的方式來解題的關鍵，這裡用個簡單的累加和的例子:

設計一個函數，輸入引數為 n ，返回 1+2+...n 的和。

public int sum(int n){
	int result = 0;
	for (int i = 1; i <= n ; i++) {
		result = result + i; 
	}
	return result;
}

想想初學 C 語言for迴圈的時候應該都有寫過上述程式碼，從 1開始遞增加到 n 這其實是典型的遞推。那如果用遞迴的思路來思考的話：

求 1+2+..n 的和（問題） -> 就是 n 加上 求 1+2+..（n-1）的和（同類的子問題）;
其中最基本的情況 1 的和為 1。

public int sum( int n ) {
	if( 1 == n) return 1;
	return n + sum(n-1);
}

可以看到遞迴的程式碼實現上是不是非常簡潔。大部分初學者思考上比較習慣於遞推，如果第一次接觸遞迴角度思考會有些不適應（或者無法獨立分析出來遞迴）也是正常。當慢慢熟悉後，會發現用遞迴的思路解決某些演演算法問題往往會非常簡單（在本篇接下來的內容中就能發現這點）。

在初學遞迴過度到熟悉遞迴這個階段，筆者建議可以考慮把一些用遞推已經解決了的問題用遞迴的思路嘗試解決，習慣遞迴思路後會開啟一片新世界。

基本遍歷（Traversal）

二元樹的遍歷是指按照一定的順序存取二元樹的所有節點。在二元樹中，有三種常見的遍歷方式，它們分別是前序遍歷、中序遍歷和後序遍歷。

先序遍歷（Preorder Traversal）

從根節點開始，首先存取根節點，然後按照前序遍歷的方式依次存取左子樹和右子樹。前序遍歷通常用於複製一棵樹或計算表示式的值。

存取順序：根節點 -> 左子樹 -> 右子樹

Leetcode 144. 二元樹的前序遍歷【簡單】

給你二元樹的根節點 root ，返回它節點值的前序遍歷。

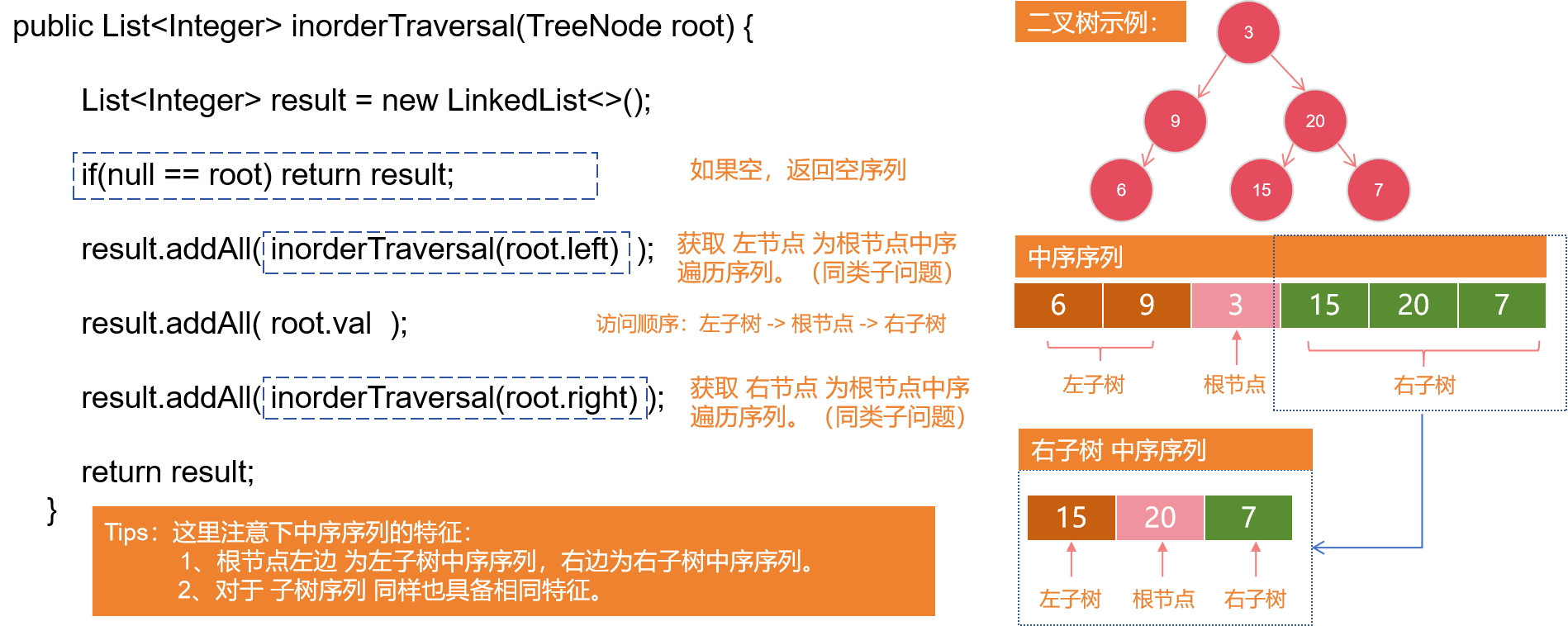
中序遍歷（Inorder Traversal）

從根節點開始，首先按照中序遍歷的方式存取左子樹，然後存取根節點，最後存取右子樹。中序遍歷通常用於存取二元搜尋樹中的節點，以升序或降序存取節點值。

存取順序：左子樹 -> 根節點 -> 右子樹

Leetcode 94. 二元樹的中遍歷【簡單】

給定一個二元樹的根節點 root ，返回它的中序遍歷。

針對後序遍歷（Postorder Traversal）從根節點開始，首先按照後序遍歷的方式存取左子樹，然後存取右子樹，最後存取根節點。後序遍歷通常用於釋放二元樹的記憶體，或計算表示式的值。存取順序：左子樹 -> 右子樹 -> 根節點，在此不過多描述相信一定能夠完成編碼。

反向構建

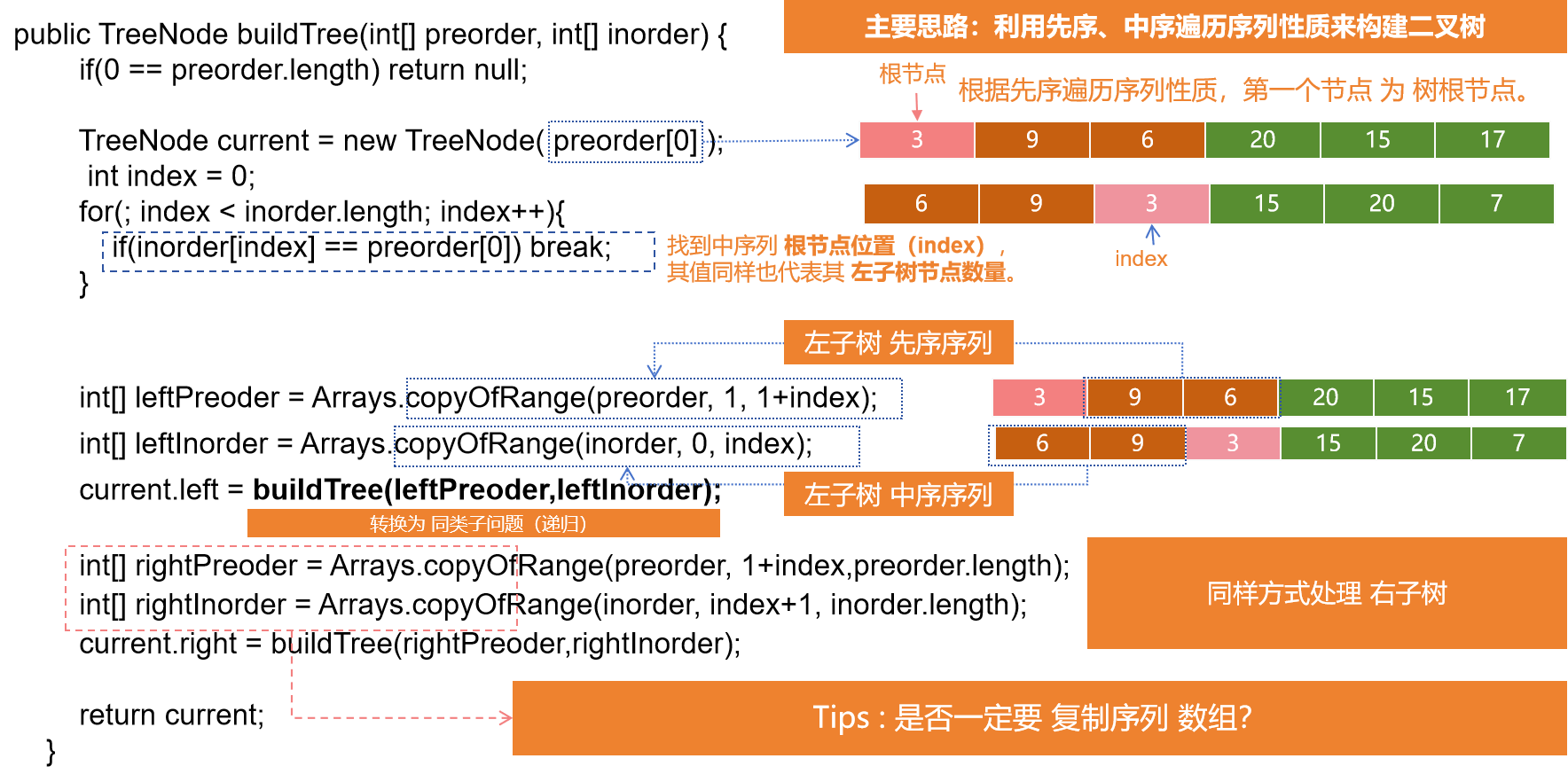
Leetcode 105. 從前序與中序遍歷序列構造二元樹【中等】

給定兩個整數陣列 preorder 和 inorder ，其中 preorder 是二元樹的先序遍歷， inorder 是同一棵樹的中序遍歷，請構造二元樹並返回其根節點。

綜合應用

本系列文章中已經介紹了連結串列、遞迴、二元樹，解決演演算法問題往往會需要綜合應用。不妨來看下下面這個問題：

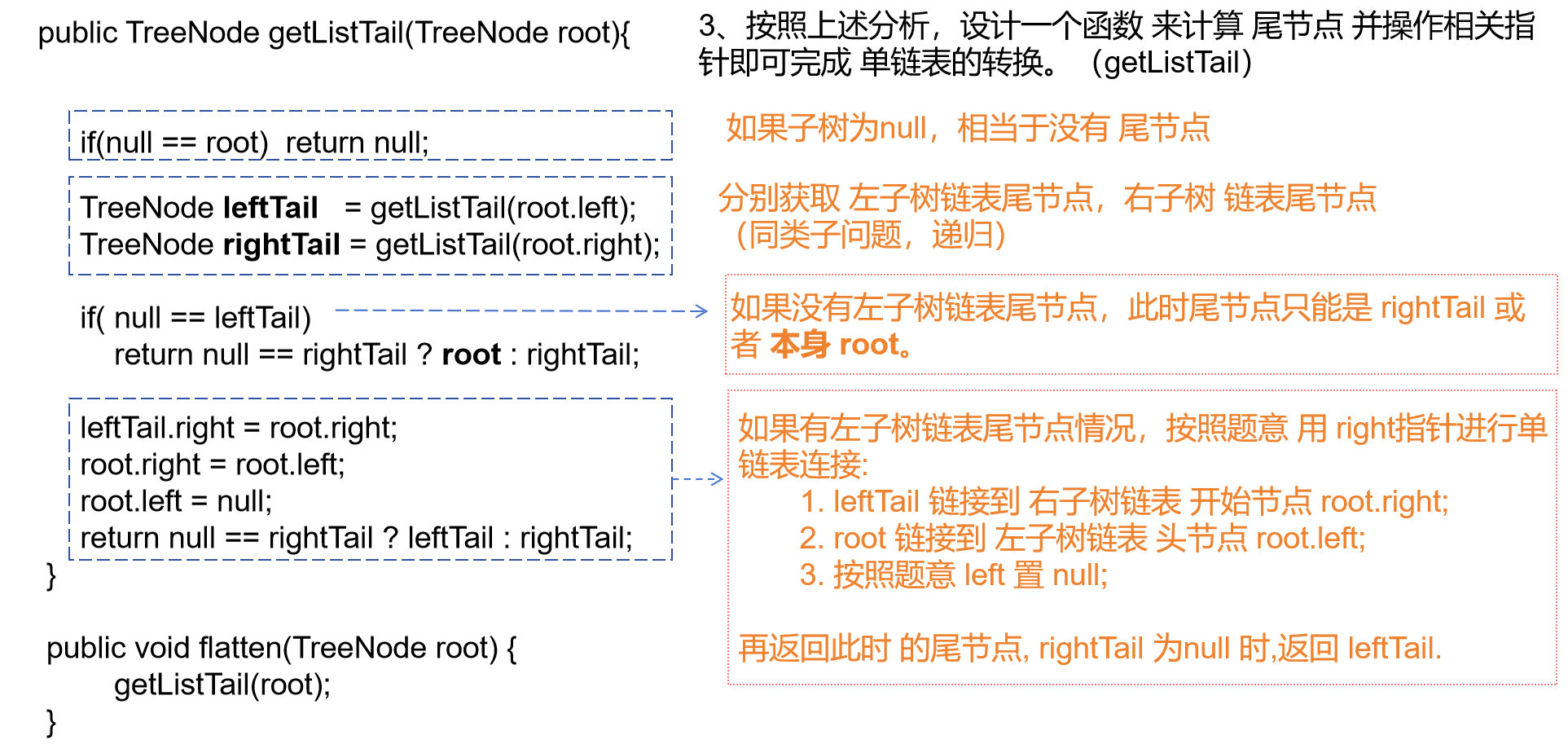
Leetcode 114. 二元樹展開為連結串列【中等】

給你二元樹的根結點 root ，請你將它展開為一個單連結串列：
展開後的單連結串列應該同樣使用 TreeNode ，其中 right 子指標指向連結串列中下一個結點，而左子指標始終為 null 。
展開後的單連結串列應該與二元樹先序遍歷順序相同。

總結下

介紹了二元樹的的一些基本概念包括：根節點、葉子節點、高度等等；
介紹了基礎演演算法遞迴的思想：「重複將問題分解為同類的子問題而解決問題的方法」；
介紹了基本的二元樹遍歷和反向構建的相關思路；
結合本系列先前文章內容，解決綜合連結串列、遞迴、二元樹的問題，靈活處理使用資料結構的特徵是關鍵。

資料結構與演演算法 | 二元樹(Binary Tree)