2023 版 Java和python開發線性代數探索
2023-10-22 12:00:16
前景提示
- 最近小夥伴問了一個題目,就是用Java開發線性代數,本身Java的能力並不是很擅長做這樣的工作,需要計算的話還是用python開發更好,方便快捷,簡單方便,但是,既然有這樣的需求還是需要進行開發的,畢竟沒有客戶會管你多麼費勁,只會說你開發不了水平不夠,這邊進行了九個小時的開發,開發了Java和python兩個版本,本文的優勢就在於系統全面,並且拿來可用,對於那些急於解決問題,完成作業的小夥伴,非常友好,因此,這篇文章對你幫助極大,希望你喜歡。
需求
- 題目如下如這樣。



分析
1、初始化不需要指定矩陣的尺寸,並且可以直接傳入資料。
- 題目一的要求翻譯一下,就是要(1)寫一個子類繼承父類別,(2)子類要有一個構造方法可以傳入double[]型別的資料,(3)列印的結果要像圖例那樣,所以要重寫showInfo方法(這是沒重寫實際執行發現的,初期沒覺得要重寫)
2、可以計算2x2矩陣的逆
- 題目翻譯:(1) 要開發一個get_inverse()在子類中(2)要增加一個判斷判斷在矩陣中全是0的時候要有判斷輸出。
3、可以做2x2的矩陣乘法
- 題目翻譯:(1) 要開發一個方法mul(m3),可以做矩陣的乘法 (2)方法之間可以互相呼叫mul().showInfo().
Java版本開發
一、 開發詳情
1、開發一個子類,如圖所示。

父類別
package com.grandfather.www.marixs;
/**
* @projectName: marixs
* @package: com.grandfathers.www.marixs
* @className: BaseMatrix
* @author: your-father
* @description: TODO
* @date: 2023-09-30 20:58
* @version: 1.0
*/
public class BaseMatrix {
// 矩陣的行列數
int m = 0, n = 0;
// 矩陣的資料
float data[];
public BaseMatrix() {
}
// 建構函式
public BaseMatrix(int m, int n) {
this.m = m;
this.n = n;
this.data = new float[m * n];
}
// 設定矩陣
public void setData(float[] data) {
this.data = data;
}
public float[] getData() {
return data;
}
// 顯示矩陣的資訊
void showInfo() {
System.out.println("-----------");
System.out.println("矩陣尺寸為: " + m + "x" + n);
System.out.println("矩陣的資料為 : ");
for (int i = 0; i < this.data.length; i++) {
System.out.println(this.data[i] + ",");
if ((i + 1) % n == 0) {
System.out.println("\n");
}
}
System.out.println("------------");
}
// 矩陣加法
BaseMatrix add(BaseMatrix m2) {
if ((this.m == m2.m) && (this.n == m2.n)) {
float[] d = new float[m * n];
for (int i = 0; i < m * n; i++) {
d[i] = this.data[i] + m2.data[i];
}
BaseMatrix baseMatrix = new BaseMatrix(m, n);
// 結果放到新的矩陣中
baseMatrix.setData(d);
return baseMatrix;
} else {
System.out.println("兩個矩陣尺寸不一致,無法做加法");
return null;
}
}
}
子類
public class Marix_2X2 extends BaseMatrix {
public static void main(String[] args) {
// 檢視矩陣
Marix_2X2 marix2X2 = new Marix_2X2();
marix2X2.setData(new float[]{1, 2, 2, 5});
marix2X2.n=2;
marix2X2.showInfo();
}
}
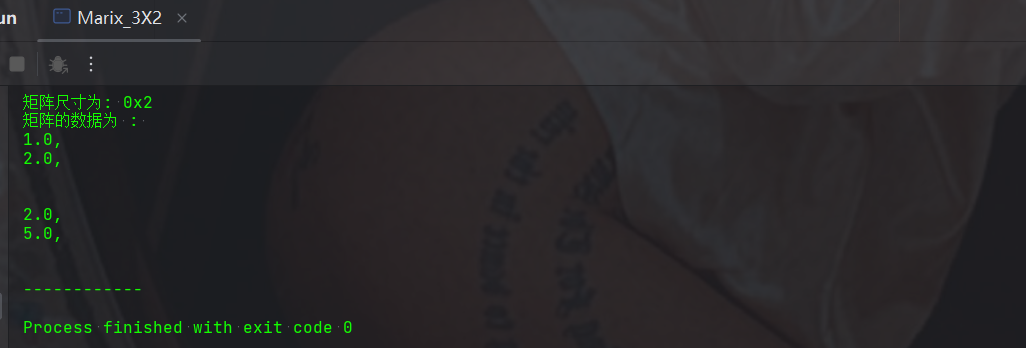
- 建個基礎的版本,可以做個繼承BaseMatrix,檢視其父類別的方法,什麼也不改就只能像上面這樣使用,可以看到,跟測試完全不一樣,列印的結果中間有個大空格,這樣不符合題目的要求,因此,需要改造。
2、根據問題修改子類,父類別,以便真實可用
解決1、初始化不需要指定矩陣的尺寸,並且可以直接傳入資料。
- 首先要在子類裡新增構造方法

public class Marix_2X2 extends BaseMatrix {
public Marix_2X2() {
}
public Marix_2X2(float[] data) {
super();
this.data = data;
createBase(data);
}
BaseMatrix createBase(float[] data) {
int m = 0, n = 0;
for (int i = 0; i < data.length; i++) {
if (i % 2 == 0) {
n = i;
} else {
m = i;
}
}
this.m = m;
this.n = n;
BaseMatrix baseMatrix = new BaseMatrix(m, n);
// 結果放到新的矩陣中
baseMatrix.setData(data);
return baseMatrix;
}
}
-
其次要重寫showInfo() 方法
// 顯示矩陣的資訊 @Override void showInfo() { System.out.println("-----------"); System.out.println("矩陣尺寸為: " + (m - 1) + "x" + n); System.out.println("矩陣的資料為 : "); for (int i = 0; i < this.data.length; i++) { System.out.print(this.data[i] + ","); if ((i + 1) % n == 0) { System.out.println(); } } System.out.println("------------"); System.out.println(); } -
最終第一個版本結果。(題目一的要求就滿足了)
package com.grandfather.www.marixs; /** * @projectName: marixs * @package: com.grandfathers.www.marixs * @className: Marix_2X2 * @author: your-father * @description: TODO * @date: 2023-09-30 21:14 * @version: 1.0 */ public class Marix_2X2 extends BaseMatrix { public Marix_2X2() { } public Marix_2X2(float[] data) { super(); this.data = data; createBase(data); } BaseMatrix createBase(float[] data) { int m = 0, n = 0; for (int i = 0; i < data.length; i++) { if (i % 2 == 0) { n = i; } else { m = i; } } this.m = m; this.n = n; BaseMatrix baseMatrix = new BaseMatrix(m, n); // 結果放到新的矩陣中 baseMatrix.setData(data); return baseMatrix; } // 顯示矩陣的資訊 @Override void showInfo() { System.out.println("-----------"); System.out.println("矩陣尺寸為: " + (m - 1) + "x" + n); System.out.println("矩陣的資料為 : "); for (int i = 0; i < this.data.length; i++) { System.out.print(this.data[i] + ","); if ((i + 1) % n == 0) { System.out.println(); } } System.out.println("------------"); System.out.println(); } public static void main(String[] args) { // 檢視矩陣 Marix_2X2 marix2X2 = new Marix_2X2(new float[]{1, 2, 2, 5}); marix2X2.showInfo(); } }
解決 2、可以計算2x2矩陣的逆
- 這裡就寫的比較複雜了,主要是一般都是按照二維陣列的處理方式處理的,而題目給的書傳入一個一維陣列,所以這裡總是要處理,一維陣列變二維,二維陣列變一維這樣的問題。
樣例一
// 判斷陣列的元素是否全為0
boolean flag = true;
private Marix_2X2 get_inverse() {
Marix_2X2 m1 = new Marix_2X2(this.data);
if (null != this.data) {
float[] newdata = this.data;
int temp = 0;
for (int i = 0; i < newdata.length; i++) {
if (newdata[i] == 0) {
temp++;
}
}
if (temp == newdata.length) {
m1.flag = false;
} else {
float[][] newdata2 = new float[this.m - 1][this.n];
newdata2 = one2Two(newdata, newdata2);
float[][] floats = gaussianElimination(newdata2);
float[] result = two2One(floats, newdata);
m1.setData(result);
return m1;
}
return m1;
} else {
System.out.println("為傳入合法的資料....");
return null;
}
}
float[][] gaussianElimination(float[][] arr) {
int i, j, k;
float tem_1, tem_2, tem_3;
int N = arr.length;
float[][] W = new float[N][2 * N];
float[][] result = new float[N][N];
// 對矩陣右半部分進行擴增
for (i = 0; i < arr.length; i++) {
for (j = 0; j < 2 * arr.length; j++) {
if (j < arr.length) {
W[i][j] = arr[i][j];
} else {
W[i][j] = (float) (j - N == i ? 1 : 0);
}
}
}
for (i = 0; i < N; i++) {
// 判斷矩陣第一行第一列的元素是否為0,若為0,繼續判斷第二行第一列元素,直到不為0,將其加到第一行
if (((int) W[i][i]) == 0) {
for (j = i + 1; j < N; j++) {
if (((int) W[j][i]) != 0) {
break;
}
}
if (j == N) {
System.out.print("這個矩陣不能求逆");
break;
}
//將前面為0的行加上後面某一行
for (k = 0; k < 2 * N; k++) {
W[i][k] += W[j][k];
}
}
//將前面行首位元素置1
tem_1 = W[i][i];
for (j = 0; j < 2 * N; j++) {
W[i][j] = W[i][j] / tem_1;
}
//將後面所有行首位元素置為0
for (j = i + 1; j < N; j++) {
tem_2 = W[j][i];
for (k = i; k < 2 * N; k++) {
W[j][k] = W[j][k] - tem_2 * W[i][k];
}
}
}
// 將矩陣前半部分標準化
for (i = N - 1; i >= 0; i--) {
for (j = i - 1; j >= 0; j--) {
tem_3 = W[j][i];
for (k = i; k < 2 * N; k++) {
W[j][k] = W[j][k] - tem_3 * W[i][k];
}
}
}
//得出逆矩陣
for (i = 0; i < N; i++) {
for (j = N; j < 2 * N; j++) {
result[i][j - N] = W[i][j];
}
}
return result;
}
/*!!!注意:
* 1.傳入的陣列裡兩個陣列的大小(一維陣列length為10,則二維陣列的行數乘列數也為10
* 2.陣列型別必須一樣
* */
public static float[][] one2Two(float[] data, float[][] da) {
int k = 0;
int hang = da.length;
int lie = 0;
if (!isAllZero(da)) {
lie = da[0].length;
} else {
lie = 1;
}
for (int i = 0; i < hang; i++) {
for (int j = 0; j < lie; j++) {
da[i][j] = data[k];
k++;
}
}
return da;
}
/*!!!注意:
* 1.傳入的陣列裡兩個陣列的大小(一維陣列length為10,則二維陣列的行數乘列數也為10
* 2.陣列型別必須一樣
* */
public static float[] two2One(float[][] da, float[] data) {
int k = 0;
int hang = da.length;
int lie = 0;
if (!isAllZero(da)) {
lie = da[0].length;
} else {
lie = 1;
}
for (int i = 0; i < hang; i++) {
for (int j = 0; j < lie; j++) {
data[k] = da[i][j];
k++;
}
}
return data;
}
private static boolean isAllZero(float[][] onwResult) {
int temp = 0;
for (float[] floats : onwResult) {
for (float aFloat : floats) {
if (aFloat == 0) {
temp++;
}
}
}
if (temp == onwResult.length) {
return true;
} else {
return false;
}
}
// 新增了全為0 的判斷
// 顯示矩陣的資訊
@Override
void showInfo() {
if (flag) {
System.out.println("-----------");
System.out.println("矩陣尺寸為: " + (m - 1) + "x" + n);
System.out.println("矩陣的資料為 : ");
for (int i = 0; i < this.data.length; i++) {
System.out.print(this.data[i] + ",");
if ((i + 1) % n == 0) {
System.out.println();
}
}
System.out.println("------------");
System.out.println();
} else {
System.out.println("行列式為0,不能求逆矩陣");
System.out.println();
}
}
測試
// 全為0的矩陣
Marix_2X2 m1 = new Marix_2X2(new float[]{0, 0, 0, 0});
Marix_2X2 tmp = m1.get_inverse();
assert tmp != null;
tmp.showInfo();
(1) 第二題第一問,全為零列印
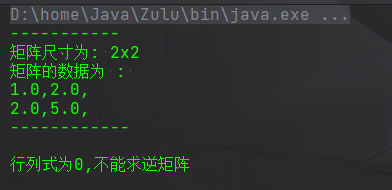
(2)第二題第二問,逆矩陣輸出

解決 3、可以做2x2的矩陣乘法
-
矩陣乘法也沒有什麼問題,但是這裡發現第一個結果跟題目的答案不一樣,因此,經過反覆debug發現是上個逆矩陣的演演算法有問題,因此這裡又修改了逆矩陣的演演算法,最終,結果一致了。
-
錯誤的輸出
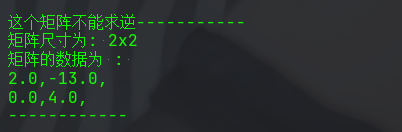
矩陣的乘法
private Marix_2X2 mul(Marix_2X2 m3) {
float[][] a = new float[this.m - 1][this.n];
one2Two(this.getData(), a);
float[][] b = new float[this.m - 1][this.n];
one2Two(m3.getData(), b);
float[][] c = new float[this.m - 1][this.n];
float[] newdata = this.data;
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a.length; j++) {
for (int k = 0; k < a.length; k++) {
c[i][j] += a[i][k] * b[k][j];
}
}
}
float[] result = two2One(c, newdata);
m3.setData(result);
return m3;
}
替換逆矩陣演演算法
//求解逆矩陣
public Marix_2X2 get_inverse_2() {
Marix_2X2 m1 = new Marix_2X2(this.data);
if (null != this.data) {
int temp = 0;
float[] onwResult = this.data;
temp = isAllZero(temp, onwResult);
if (temp == onwResult.length) {
m1.flag = false;
} else {
float[][] floats = new float[this.m - 1][this.n];
float[][] floats2 = one2Two(m1.getData(), floats);
int row = floats2.length;
float[][] floats1 = CopyArry(floats2);
float[][] floats6 = new float[row][row];
float[][] floats7 = AdjointMatrix(floats1);
for (int i = 0; i < row; i++) {
for (int i1 = 0; i1 < row; i1++) {
floats6[i][i1] = floats7[i][i1] / ArrayCount(floats1, row);
}
}
float[] result = two2One(floats6, onwResult);
m1.setData(result);
}
return m1;
} else {
System.out.println("為傳入合法的資料....");
return null;
}
}
//矩陣的複製
public static float[][] CopyArry(float[][] floats) {
int row = floats.length;
float[][] floats1 = new float[row][row];
for (int i = 0; i < row; i++) {
for (int i1 = 0; i1 < row; i1++) {
floats1[i][i1] = floats[i][i1];
}
}
return floats1;
}
//矩陣求伴隨矩陣
public static float[][] AdjointMatrix(float[][] floats) {
int row = floats.length;
float[][] floats1 = CopyArry(floats);
float[][] floats4 = new float[row][row];
for (int i = 0; i < row; i++) {
for (int i1 = 0; i1 < row; i1++) {
floats4[i1][i] = (-1) * (((i + i1) % 2) == 1 ? 1 : -1) * ArrayCount(RemoveRC(floats1, row, i, i1), row - 1);
}
}
return floats4;
}
// 計算陣列行列式方法
public static float ArrayCount(float a[][], int n) {
float p = 0;
for (int k = 0; k <= n - 2; k++) {
for (int r = k + 1; r <= n - 1; r++) {
if (a[k][k] == 0) {
try {
ArrayChange(a, k, n);
} catch (Exception e) {
System.out.println(e.getMessage());
return 0;
}
}
p = -(a[r][k] / a[k][k]);
for (int i = k; i <= n - 1; i++) {
a[r][i] = a[k][i] * p + a[r][i];
}
}
}
float result = 1;
for (int i = 0; i <= n - 1; i++) {
result *= a[i][i];
}
return result;
}
/**
* @param a 傳入的陣列
* @param k 出現問題的元素的行和列的座標數值
* @param n 陣列的長度 ,雖然是從0 標開始,但是這裡仍然使用n來計數
*/
public static void ArrayChange(float a[][], int k, int n) {
float b[] = new float[n - k];
int c = k;
for (int i = k + 1; i <= n - 1; i++) {
if (a[i][k] != 0) {
c = i;
}
}
if (c == k) {
throw new RuntimeException("高斯求解失敗");
}
int w = 0;
for (int i = k; i <= n - 1; i++) {
b[w] = a[k][i];
a[k][i] = a[c][i];
a[c][i] = b[w];
w++;
}
}
//去掉固定的行和列的行列式
public static float[][] RemoveRC(float[][] floats, int n, int p, int q) {
float[][] floats1 = new float[n][n];
float[][] floats2 = new float[n - 1][n - 1];
ArrayList<Float> arrayList = new ArrayList<>((n - 1) * (n - 1));
for (int i = 0; i <= n - 1; i++) {
for (int i1 = 0; i1 <= n - 1; i1++) {
floats1[i][i1] = floats[i][i1];
}
}
for (int i = 0; i <= n - 1; i++) {
for (int i1 = 0; i1 <= n - 1; i1++) {
if (i == p || i1 == q) {
} else {
arrayList.add(floats[i][i1]);
}
}
}
Object[] objects = arrayList.toArray();
int index = 0;
for (int i = 0; i < n - 1; i++) {
for (int i1 = 0; i1 < n - 1; i1++) {
floats2[i][i1] = (float) objects[index];
index++;
}
}
return floats2;
}
(1) 第三題第一問,逆矩陣乘法
-
測試程式碼
// 矩陣的乘法 Marix_2X2 m2 = new Marix_2X2(new float[]{2, 5, 1, 3}); Marix_2X2 m3 = new Marix_2X2(new float[]{4, -6, 2, 1}); m2.get_inverse_2().mul(m3).showInfo();
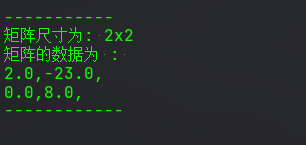
(2)第三題第二問,複合乘法
-
測試程式碼
// 矩陣的複合乘法 Marix_2X2 m4 = new Marix_2X2(new float[]{1, 4, -1, 2}); Marix_2X2 m5 = new Marix_2X2(new float[]{3, 1, 0, -1}); Marix_2X2 m6 = new Marix_2X2(new float[]{2, 0, -1, 1}); m4.get_inverse_2().mul(m5).mul(m6.get_inverse_2()).showInfo();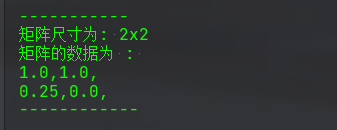
二、最終完整版
- 父類別
package com.grandfathers.www.exersice;/**
* @author: MrLiu
* @createTime: 2023/09/30 20:58
* @description: xxx
*/
/**
* @projectName: anlysistSentence
* @package: com.grandfathers.www.exersice
* @className: BaseMatrix
* @author: your-father
* @description: TODO
* @date: 2023-09-30 20:58
* @version: 1.0
*/
public class BaseMatrix {
// 矩陣的行列數
int m = 0, n = 0;
// 矩陣的資料
float data[];
public BaseMatrix() {
}
// 建構函式
public BaseMatrix(int m, int n) {
this.m = m;
this.n = n;
this.data = new float[m * n];
}
// public BaseMatrix(float[] data) {
// this.data = data;
// createBase(data);
// }
// 設定矩陣睡覺
public void setData(float[] data) {
this.data = data;
}
public float[] getData() {
return data;
}
// 顯示矩陣的資訊
void showInfo() {
System.out.println("-----------");
System.out.println("矩陣尺寸為: " + m + "x" + n);
System.out.println("矩陣的資料為 : ");
for (int i = 0; i < this.data.length; i++) {
System.out.println(this.data[i] + ",");
if ((i + 1) % n == 0) {
System.out.println("\n");
}
}
System.out.println("------------");
}
// 矩陣加法
BaseMatrix add(BaseMatrix m2) {
if ((this.m == m2.m) && (this.n == m2.n)) {
float[] d = new float[m * n];
for (int i = 0; i < m * n; i++) {
d[i] = this.data[i] + m2.data[i];
}
BaseMatrix baseMatrix = new BaseMatrix(m, n);
// 結果放到新的矩陣中
baseMatrix.setData(d);
return baseMatrix;
} else {
System.out.println("兩個矩陣尺寸不一致,無法做加法");
return null;
}
}
}
-
子類
package com.grandfathers.www.exersice;/** * @author: MrLiu * @createTime: 2023/09/30 21:14 * @description: xxx */ import java.util.ArrayList; import java.util.Objects; import static java.lang.Math.pow; /** * @projectName: anlysistSentence * @package: com.grandfathers.www.exersice * @className: Marix_2X2 * @author: your-father * @description: TODO * @date: 2023-09-30 21:14 * @version: 1.0 */ public class Marix_2X2 extends BaseMatrix { // 判斷陣列的元素是否全為0 boolean flag = true; public Marix_2X2(float[] data) { super(); this.data = data; createBase(data); } BaseMatrix createBase(float[] data) { int m = 0, n = 0; for (int i = 0; i < data.length; i++) { if (i % 2 == 0) { n = i; } else { m = i; } } this.m = m; this.n = n; BaseMatrix baseMatrix = new BaseMatrix(m, n); // 結果放到新的矩陣中 baseMatrix.setData(data); return baseMatrix; } // 顯示矩陣的資訊 @Override void showInfo() { if (flag) { System.out.println("-----------"); System.out.println("矩陣尺寸為: " + (m - 1) + "x" + n); System.out.println("矩陣的資料為 : "); for (int i = 0; i < this.data.length; i++) { System.out.print(this.data[i] + ","); if ((i + 1) % n == 0) { System.out.println(); } } System.out.println("------------"); System.out.println(); } else { System.out.println("行列式為0,不能求逆矩陣"); System.out.println(); } } /** * <p>使用高斯消元法對矩陣進行求逆<p/> * * @param arr 二維矩陣 * @return 矩陣的逆 */ float[][] gaussianElimination(float[][] arr) { int i, j, k; float tem_1, tem_2, tem_3; int N = arr.length; float[][] W = new float[N][2 * N]; float[][] result = new float[N][N]; // 對矩陣右半部分進行擴增 for (i = 0; i < arr.length; i++) { for (j = 0; j < 2 * arr.length; j++) { if (j < arr.length) { W[i][j] = arr[i][j]; } else { W[i][j] = (float) (j - N == i ? 1 : 0); } } } for (i = 0; i < N; i++) { // 判斷矩陣第一行第一列的元素是否為0,若為0,繼續判斷第二行第一列元素,直到不為0,將其加到第一行 if (((int) W[i][i]) == 0) { for (j = i + 1; j < N; j++) { if (((int) W[j][i]) != 0) break; } if (j == N) { System.out.print("這個矩陣不能求逆"); break; } //將前面為0的行加上後面某一行 for (k = 0; k < 2 * N; k++) { W[i][k] += W[j][k]; } } //將前面行首位元素置1 tem_1 = W[i][i]; for (j = 0; j < 2 * N; j++) { W[i][j] = W[i][j] / tem_1; } //將後面所有行首位元素置為0 for (j = i + 1; j < N; j++) { tem_2 = W[j][i]; for (k = i; k < 2 * N; k++) { W[j][k] = W[j][k] - tem_2 * W[i][k]; } } } // 將矩陣前半部分標準化 for (i = N - 1; i >= 0; i--) { for (j = i - 1; j >= 0; j--) { tem_3 = W[j][i]; for (k = i; k < 2 * N; k++) { W[j][k] = W[j][k] - tem_3 * W[i][k]; } } } //得出逆矩陣 for (i = 0; i < N; i++) { for (j = N; j < 2 * N; j++) { result[i][j - N] = W[i][j]; } } return result; } /*!!!注意: * 1.傳入的陣列裡兩個陣列的大小(一維陣列length為10,則二維陣列的行數乘列數也為10 * 2.陣列型別必須一樣 * */ public static float[][] one2Two(float[] data, float[][] da) { int k = 0; int hang = da.length; int lie = 0; if (!isAllZero(da)) { lie = da[0].length; } else { lie = 1; } for (int i = 0; i < hang; i++) { for (int j = 0; j < lie; j++) { da[i][j] = data[k]; k++; } } return da; } /*!!!注意: * 1.傳入的陣列裡兩個陣列的大小(一維陣列length為10,則二維陣列的行數乘列數也為10 * 2.陣列型別必須一樣 * */ public static float[] two2One(float[][] da, float[] data) { int k = 0; int hang = da.length; int lie = 0; if (!isAllZero(da)) { lie = da[0].length; } else { lie = 1; } for (int i = 0; i < hang; i++) { for (int j = 0; j < lie; j++) { data[k] = da[i][j]; k++; } } return data; } private Marix_2X2 mul(Marix_2X2 m3) { float[][] a = new float[this.m - 1][this.n]; one2Two(this.getData(), a); float[][] b = new float[this.m - 1][this.n]; one2Two(m3.getData(), b); float[][] c = new float[this.m - 1][this.n]; float[] newdata = this.data; for (int i = 0; i < a.length; i++) { for (int j = 0; j < a.length; j++) { for (int k = 0; k < a.length; k++) { c[i][j] += a[i][k] * b[k][j]; } } } float[] result = two2One(c, newdata); m3.setData(result); return m3; } //正交化 public static float[][] Orthogonalization(float[][] floats) { float[][] floats1 = CopyArry(floats); int row = floats1.length; ArrayList<float[]> arrayList = new ArrayList<>(); for (int i = 0; i < row; i++) { arrayList.add(i, new float[row]); for (int i1 = 0; i1 < row; i1++) { arrayList.get(i)[i1] = floats1[i1][i]; } } for (int i = 0; i < row; i++) { float[] floats2 = new float[row]; CopySingleArray(arrayList.get(i), floats2); floats2 = XiuGindexN(floats1, i); CopySingleArray(floats1[i], floats2); } float[][] result = new float[row][row]; for (int i = 0; i < row; i++) { for (int i1 = 0; i1 < row; i1++) { result[i1][i] = floats1[i][i1]; } } return result; } //定義單一陣列的複製 /** * @param floats1 即將要被修改的陣列 * @param floats2 參考陣列 * 修改了floats 1 陣列 */ public static void CopySingleArray(float[] floats1, float[] floats2) { for (int i = 0; i < floats2.length; i++) { floats1[i] = floats2[i]; } } //定義回溯積累的正交化中間方法 /** * @param floats 傳入的陣列 * @param index 陣列的行數 * @return 結果陣列 * 根據行數來求出第index個 正交化的行向量, */ public static float[] XiuGindexN(float[][] floats, int index) { int row = floats.length; float[] result = new float[row]; float[][] floats1 = CopyArry(floats); if (index == 0) { CopySingleArray(result, floats1[index]); } else { for (int i = index - 1; i >= 0; i--) { float p = DeterminantProduct(floats1[index], floats1[i]) / DeterminantProduct(floats1[i], floats1[i]); float[] floats2 = NumberTimesArray(-p, floats1[i]); result = DeterminAntddition(result, floats2); } result = DeterminAntddition(result, floats1[index]); } return result; } //定義一個數和陣列的乘法 public static float[] NumberTimesArray(float f, float[] floats) { int row = floats.length; float[] floats1 = new float[row]; for (int i = 0; i < row; i++) { floats1[i] = floats[i] * f; } return floats1; } //定義一個求兩個陣列積的方法 /** * @param floats1 傳入的第一個陣列 * @param floats2 傳入的第二個陣列 * @return 返回一個結果,不對原有的引數地址內容進行修改,是一個可靠的方法 */ public static float DeterminantProduct(float[] floats1, float[] floats2) { float result = 0; int row = floats1.length; for (int i = 0; i < row; i++) { result += floats1[i] * floats2[i]; } return result; } //定義正交基本矩陣計算 public float[][] OrthogonalBasic(float[][] floats) { int row = floats.length; float[][] floats1 = getData(new Marix_2X2(this.getData()).Transpose()); return Orthogonalization(floats1); } //定義正交基本單位化計算 public static float[][] OrthogonalasicUnit(float[][] floats) { int row = floats.length; float[][] floats1 = CopyArry(floats); return Unitization(new Marix_2X2(two2One(floats1, new float[row])).OrthogonalBasic(floats1)); } //矩陣的單位化 //修改原矩陣 public static float[][] Unitization(float[][] floats) { float[][] floats1 = CopyArry(floats); int row = floats1.length; for (int i = 0; i < row; i++) { float abVe = IntermediateAbsoluteValue(floats1, i); for (int i1 = 0; i1 < row; i1++) { floats1[i1][i] = floats1[i1][i] / abVe; } } return floats1; } //定義單位化中間方法 /** * @param floats 需要傳入的陣列 * @param index 陣列的列 * @return 返回該列的 單位化數值 * 不修改原矩陣 */ public static float IntermediateAbsoluteValue(float[][] floats, int index) { float[][] floats1 = CopyArry(floats); int row = floats1.length; int index1 = index; float abVe = 0; while (index == index1) { for (int i = 0; i < row; i++) { abVe += floats1[i][index] * floats1[i][index]; } index++; } return (float) Math.sqrt(abVe); } //定義陣列的加法 /** * @param floats1 傳入的第一個陣列 * @param floats2 傳入的第二個陣列 * @return 返回一個新的陣列,不對原有的引數地址內容進行修改,是一個可靠的方法 */ public static float[] DeterminAntddition(float[] floats1, float[] floats2) { int row = floats1.length; float[] floats = new float[row]; for (int i = 0; i < row; i++) { floats[i] = floats1[i] + floats2[i]; } return floats; } //求解逆矩陣 public Marix_2X2 get_inverse_2() { Marix_2X2 m1 = new Marix_2X2(this.data); if (null != this.data) { int temp = 0; float[] onwResult = this.data; temp = isAllZero(temp, onwResult); if (temp == onwResult.length) { m1.flag = false; } else { float[][] floats = new float[this.m - 1][this.n]; float[][] floats2 = one2Two(m1.getData(), floats); int row = floats2.length; float[][] floats1 = CopyArry(floats2); float[][] floats6 = new float[row][row]; float[][] floats7 = AdjointMatrix(floats1); for (int i = 0; i < row; i++) { for (int i1 = 0; i1 < row; i1++) { floats6[i][i1] = floats7[i][i1] / ArrayCount(floats1, row); } } float[] result = two2One(floats6, onwResult); m1.setData(result); } return m1; } else { System.out.println("為傳入合法的資料...."); return null; } } private static int isAllZero(int temp, float[] onwResult) { for (int i = 0; i < onwResult.length; i++) { if (onwResult[i] == 0) { temp++; } } return temp; } private static boolean isAllZero(float[][] onwResult) { int temp = 0; for (float[] floats : onwResult) { for (float aFloat : floats) { if (aFloat == 0) { temp++; } } } if (temp == onwResult.length) { return true; } else { return false; } } //矩陣的複製 public static float[][] CopyArry(float[][] floats) { int row = floats.length; float[][] floats1 = new float[row][row]; for (int i = 0; i < row; i++) { for (int i1 = 0; i1 < row; i1++) { floats1[i][i1] = floats[i][i1]; } } return floats1; } //矩陣求伴隨矩陣 public static float[][] AdjointMatrix(float[][] floats) { int row = floats.length; float[][] floats1 = CopyArry(floats); float[][] floats4 = new float[row][row]; for (int i = 0; i < row; i++) { for (int i1 = 0; i1 < row; i1++) { floats4[i1][i] = (-1) * (((i + i1) % 2) == 1 ? 1 : -1) * ArrayCount(RemoveRC(floats1, row, i, i1), row - 1); } } return floats4; } //去掉固定的行和列的行列式 public static float[][] RemoveRC(float[][] floats, int n, int p, int q) { float[][] floats1 = new float[n][n]; float[][] floats2 = new float[n - 1][n - 1]; ArrayList<Float> arrayList = new ArrayList<>((n - 1) * (n - 1)); for (int i = 0; i <= n - 1; i++) { for (int i1 = 0; i1 <= n - 1; i1++) { floats1[i][i1] = floats[i][i1]; } } for (int i = 0; i <= n - 1; i++) { for (int i1 = 0; i1 <= n - 1; i1++) { if (i == p || i1 == q) { } else { arrayList.add(floats[i][i1]); } } } Object[] objects = arrayList.toArray(); int index = 0; for (int i = 0; i < n - 1; i++) { for (int i1 = 0; i1 < n - 1; i1++) { floats2[i][i1] = (float) objects[index]; index++; } } return floats2; } // 計算陣列行列式方法 public static float ArrayCount(float a[][], int n) { float p = 0; for (int k = 0; k <= n - 2; k++) { for (int r = k + 1; r <= n - 1; r++) { if (a[k][k] == 0) { try { ArrayChange(a, k, n); } catch (Exception e) { System.out.println(e.getMessage()); return 0; } } p = -(a[r][k] / a[k][k]); for (int i = k; i <= n - 1; i++) { a[r][i] = a[k][i] * p + a[r][i]; } } } float result = 1; for (int i = 0; i <= n - 1; i++) { result *= a[i][i]; } return result; } //行列式行互換方法 /** * @param a 傳入的陣列 * @param k 出現問題的元素的行和列的座標數值 * @param n 陣列的長度 ,雖然是從0 標開始,但是這裡仍然使用n來計數 */ public static void ArrayChange(float a[][], int k, int n) { float b[] = new float[n - k]; int c = k; for (int i = k + 1; i <= n - 1; i++) { if (a[i][k] != 0) { c = i; } } if (c == k) { throw new RuntimeException("高斯求解失敗"); } int w = 0; for (int i = k; i <= n - 1; i++) { b[w] = a[k][i]; a[k][i] = a[c][i]; a[c][i] = b[w]; w++; } } //矩陣轉置的方法 public Marix_2X2 Transpose() { Marix_2X2 marix2X2 = new Marix_2X2(this.data); float[][] floats1 = new float[this.m - 1][this.n]; float[][] floats2 = one2Two(marix2X2.getData(), floats1); for (int i = 0; i < floats2.length - 1; i++) { for (int j = 0; j < floats2[i].length; j++) { float temp = floats2[i][j]; floats2[i][j] = floats2[j][i]; floats2[j][i] = temp; } } float[] floats3 = this.data; float[] floats = two2One(floats2, floats3); marix2X2.setData(floats); return marix2X2; } /** * 求(h,v)位置的餘子式 * * @param matrix * @param h * @param v * @return */ public float[][] confactor(float[][] matrix, int h, int v) { float[][] result = new float[matrix.length - 1][matrix[0].length - 1]; for (int i = 0; i < result.length; i++) { if (i < h - 1) { for (int j = 0; j < result[i].length; j++) { if (j < v - 1) { result[i][j] = matrix[i][j]; } else { result[i][j] = matrix[i][j + 1]; } } } else { for (int j = 0; j < result[i].length; j++) { if (j < v - 1) { result[i][j] = matrix[i + 1][j]; } else { result[i][j] = matrix[i + 1][j + 1]; } } } } return result; } private static float[][] getData(Marix_2X2 m8) { float[][] floats1 = new float[m8.m - 1][m8.n]; float[][] floats2 = one2Two(m8.getData(), floats1); return floats2; } public static void main(String[] args) { // 檢視矩陣 Marix_2X2 marix2X2 = new Marix_2X2(new float[]{1, 2, 2, 5}); marix2X2.showInfo(); // 全為0的矩陣 Marix_2X2 m1 = new Marix_2X2(new float[]{0, 0, 0, 0}); Marix_2X2 tmp = m1.get_inverse_2(); assert tmp != null; tmp.showInfo(); // 求矩陣的逆矩陣 Marix_2X2 m0 = new Marix_2X2(new float[]{1, 2, 2, 5}); Marix_2X2 tmp0 = m0.get_inverse_2(); assert tmp0 != null; tmp0.showInfo(); // 矩陣的乘法 Marix_2X2 m2 = new Marix_2X2(new float[]{2, 5, 1, 3}); Marix_2X2 m3 = new Marix_2X2(new float[]{4, -6, 2, 1}); m2.get_inverse_2().mul(m3).showInfo(); // 矩陣的複合乘法 Marix_2X2 m4 = new Marix_2X2(new float[]{1, 4, -1, 2}); Marix_2X2 m5 = new Marix_2X2(new float[]{3, 1, 0, -1}); Marix_2X2 m6 = new Marix_2X2(new float[]{2, 0, -1, 1}); m4.get_inverse_2().mul(m5).mul(m6.get_inverse_2()).showInfo(); } }
三、其他相關方法的測試
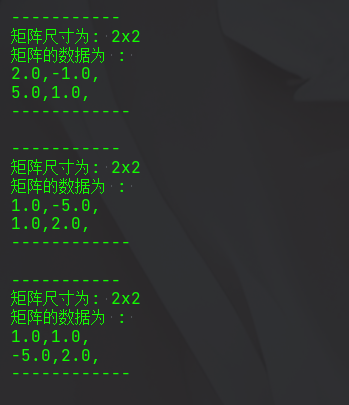
// 轉置
Marix_2X2 m7 = new Marix_2X2(new float[]{2, 5, -1, 1});
Marix_2X2 transpose = m7.Transpose();
transpose.showInfo();
// 伴隨矩陣
Marix_2X2 m8 = new Marix_2X2(new float[]{2, 5, -1, 1});
float[][] floats = m8.AdjointMatrix(getData(m8));
m8.setData(two2One(floats, m8.getData()));
m8.showInfo();
// 餘子式
m8.setData(two2One(m8.confactor(getData(m8), 2, 2), m8.getData()));
m8.Transpose();
m8.showInfo();
Python版本開發
- 都是物件導向的語言,因此操作步驟也是大同小異。
一、python程式碼
1、匯入 包
# 這個一定要匯入,不然的話,是用不了的
import numpy as np
2、建立陣列
A = np.array([[1,2],[2,5]])
3、列印陣列
# 矩陣資訊列印
def showInfo(x):
print("------------")
print("矩陣的尺寸為:",np.shape(x)[0],"x",np.shape(x)[1])
print(x)
print("------------")
4、求矩陣的逆
# 求逆矩陣
def getInverse(x):
if(np.all(x==0)):
print("行列為0,不能求逆矩陣")
else:
B = np.linalg.inv(x)
print("逆矩陣")
return B
5、矩陣的乘法
# 矩陣乘法
def mul(x,y):
c = np.matmul(x,y)
return c
6、完整版
import numpy as np
from numpy import *
# 矩陣資訊列印
def showInfo(x):
print("------------")
print("矩陣的尺寸為:",np.shape(x)[0],"x",np.shape(x)[1])
print(x)
print("------------")
# 求逆矩陣
def getInverse(x):
if(np.all(x==0)):
print("行列為0,不能求逆矩陣")
else:
B = np.linalg.inv(x)
print("逆矩陣")
return B
# 矩陣乘法
def mul(x,y):
c = np.matmul(x,y)
return c
def main():
pass
if __name__ == '__main__':
main()
A = np.array([[1,2],[2,5]])
showInfo(A)
B = np.array([[0,0],[0,0]])
getInverse(B)
H = getInverse(A)
showInfo(H)
print("-----矩陣乘法-------")
C = np.array([[2,5],[1,3]])
D = np.array([[4,-6],[2,1]])
m2 = getInverse(C)
result1 = mul(m2,D)
showInfo(result1)
print("-----混合乘法-------")
E = np.array([[1,4],[-1,2]])
F = np.array([[3,1],[0,-1]])
G = np.array([[2,0],[-1,1]])
m3 = getInverse(E)
result2 = mul(m3,F)
m4 = getInverse(G)
result3 = mul(result2,m4)
showInfo(result3)
7、測試結果


- 明顯可以看到python的寫法比Java的更加簡潔,容易理解,因此,這種題目如果可以自己選擇,最好使用python開發。
8、拓展其他功能
# 求單位矩陣
def singleArray(x):
F = np.eye(x)
return F
# 矩陣轉置
def transArray(x):
H = x.T
return H
# 計算行列式的值
def getValue(x):
H = np.linalg.det(x)
return H
# A的伴隨矩陣
def adjointMatrix(A):
n,_=A.shape #獲取階數n
Am=np.zeros((n,n)) #Am初始化為零陣
for i in range(n): #每一行
for j in range(n): #每一列
Am[i,j]=Aij(A,i,j) #伴隨陣元素
return Am.T
#代數餘子式
def Aij(A,i,j):
up=np.hstack((A[:i,:j],A[:i,j+1:])) #橫向連線上方片段
lo=np.hstack((A[i+1:,:j],A[i+1:,j+1:])) #橫向連線下方片段
M=np.vstack((up,lo)) #縱向連線
return ((-1)**(i+j))*np.linalg.det(M) #代數餘子式
# 求代數餘子式
def cofactor(matrix, i, j):
m = np.delete(matrix, i, axis=0)
m = np.delete(m, j, axis=1)
return np.linalg.det(m)
def cofactor_matrix(matrix):
n = matrix.shape[0]
cofactors = np.zeros((n, n))
for i in range(n):
for j in range(n):
cofactors[i, j] = (-1) ** (i + j) * cofactor(matrix, i, j)
return cofactors
-
測試程式碼
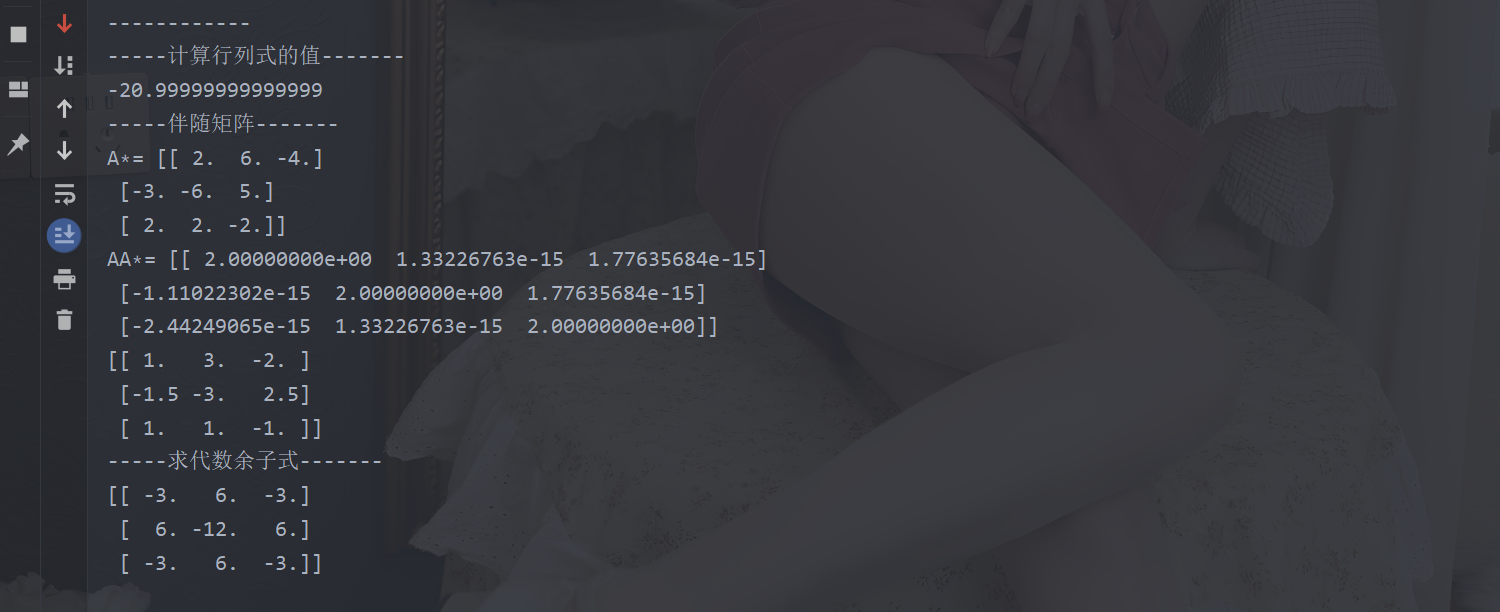
if __name__ == '__main__': print("-----單位矩陣-------") H =np.array([[1,2,3],[4,5,6],[6,1,3]]) lie = np.shape(H)[1] result4=singleArray(lie) showInfo(result4) print("-----轉置-------") result5=transArray(H) showInfo(result5) print("-----計算行列式的值-------") I =np.array([[1,1,1],[1,1,0],[1,1,3]]) result6=getValue(H) print(result6) print("-----伴隨矩陣-------") #設定矩陣A A1=np.array([[1,2,3],[2,2,1],[3,4,3]]) Am=adjointMatrix(A1) #A的伴隨陣 print("A∗=",Am) print("AA∗=",np.matmul(A1,Am)) # 也是求伴隨,結果跟上邊不一樣 B1=np.linalg.inv(A1) A_bs = B1*np.linalg.det(A) print(A_bs) print("-----求代數餘子式-------") A3 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 求解餘子式矩陣 C3 = cofactor_matrix(A3) print(C3) -
測試結果

總結
-
明顯的可以看出Java開發線性代數的程式碼量多於python好多,同時,複雜度和便於理解方面也是相形見拙,因為Java是一門開發網站的程式語言,因此處理科學計算類問題功能弱於python,因此,如果沒有特殊要求,建議使用python開發這類題目,或者用更加偏向數學的matlab開發,本文的很多程式碼也是參照了別人的程式碼,屬於利用拼接的方式,最終完成了題目的所有要求。
-
因為開發這個人和借鑑資料實在混雜,最後找找測測,使用了大量的時間,希望大家多多點贊,關注,支援,特此感謝,你的支援就是每位用心寫作的博主最大的動力,只有每位博主共同努力,你才能更好的完成作業,更便捷的找到答案,生態區才能活躍,技術才能發展,才有更璀璨的未來,因此不要林西你的支援點贊,關注。
十年磨一劍,一劍破萬法