umich cv-4-1 折積網路基本組成部分介紹
這節課中介紹了折積網路的基本組成部分(全連線層,啟用函數,折積層,池化層,標準化等),下節課討論了折積神經網路的發展歷史以及幾種經典結構是如何構建的
前言
在之前提到的全連線神經網路中,我們直接把一個比如說32 * 32 * 3的影象展開成一個3072*1的向量,然後使用向量與權重矩陣點積得到結果,這實際上是不太合理的,從某種意義上說,我們破壞了原本影象的空間資訊,把它簡單的看成一個一維向量,而在折積神經網路中,我們引入了折積層,能夠幫助我們在儲存原本影象的空間資訊的情況下,對影象特徵進行提取
折積層
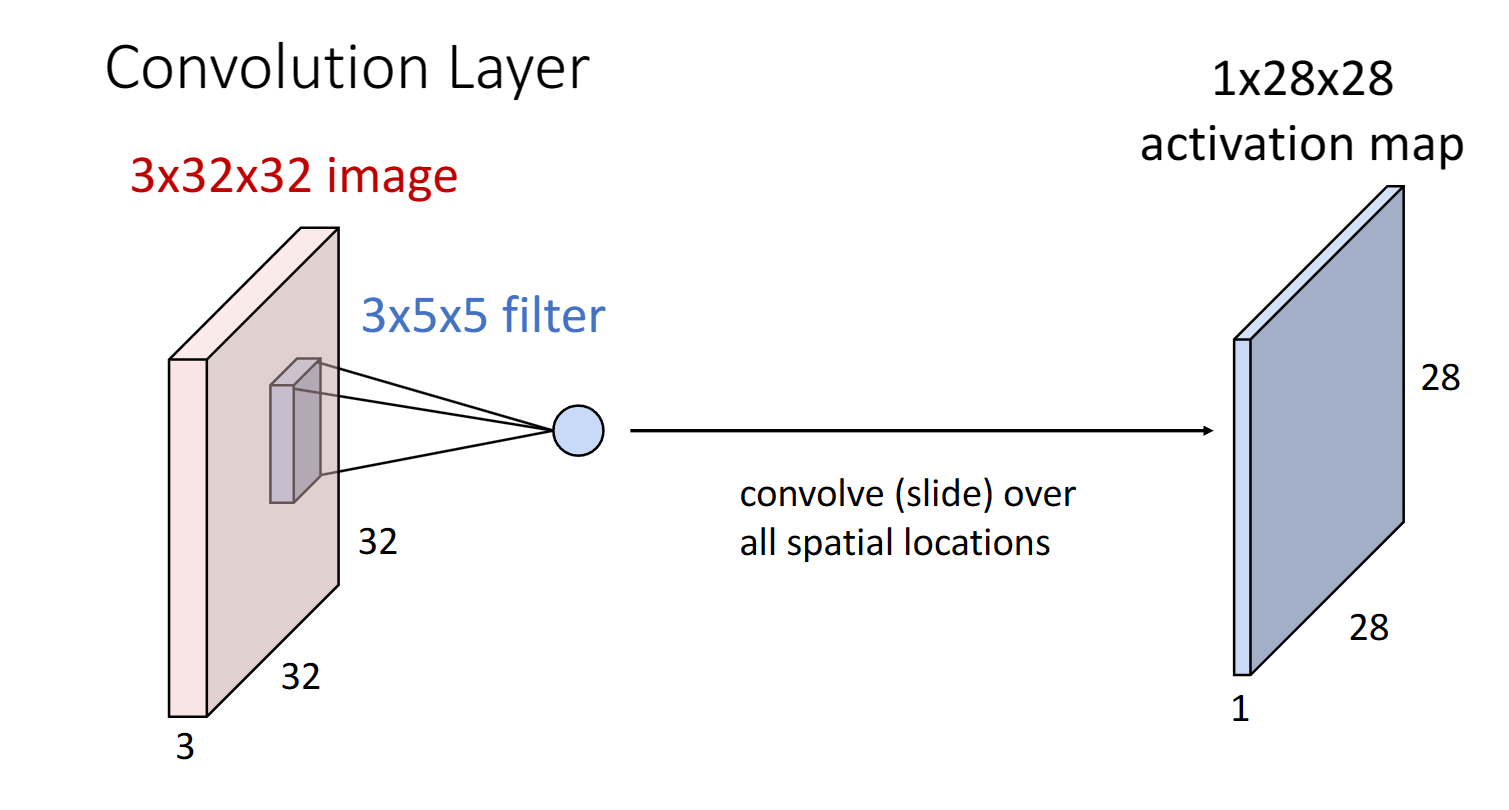
如上圖所示我們引入了一個折積核或者說filter,與原始影象進行折積運算,就是我們把折積核在原始影象上從起始位置開始滑動,依次對每個5 * 5的區域與filter點積,再加上偏置項,其實就是進行$W^{T}x + b$的運算,這樣一個區域得到一個輸出,最終一行我們可以得到$32 - 5 + 1 = 28$個輸出結果,也就意味著最終我們可以得到一張$1 \times 28 \times 28$的啟用圖
更進一步地,我們可以使用不同的filter,來獲得不同的啟用圖,組成我們的折積層:

更一般地形式:
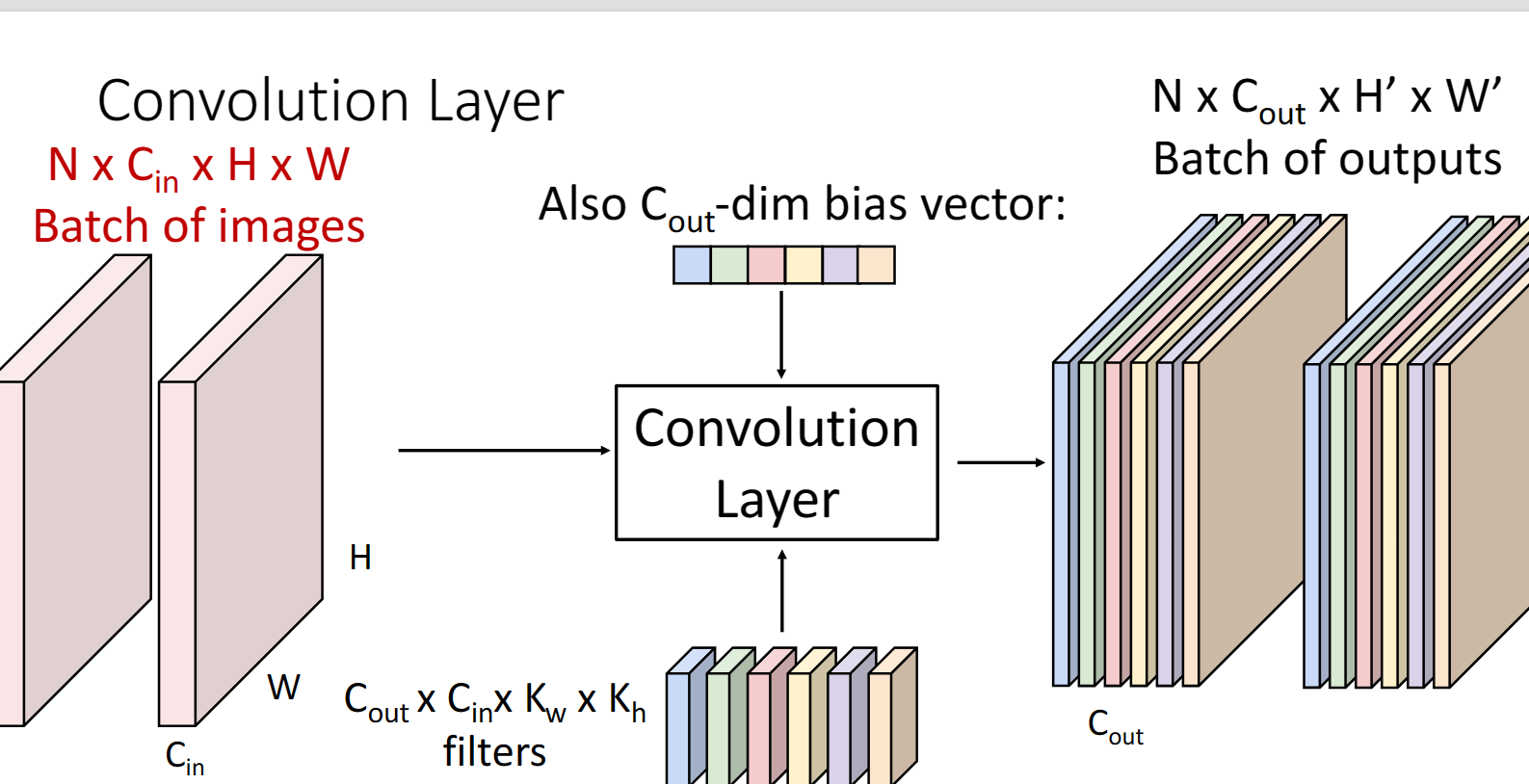
我們可以看到$C_{out}$代表著一個折積層中filter的數目,同樣也與輸出層的維度保持一致,而$C_{in}$一般都是與上一層的輸入保持一致
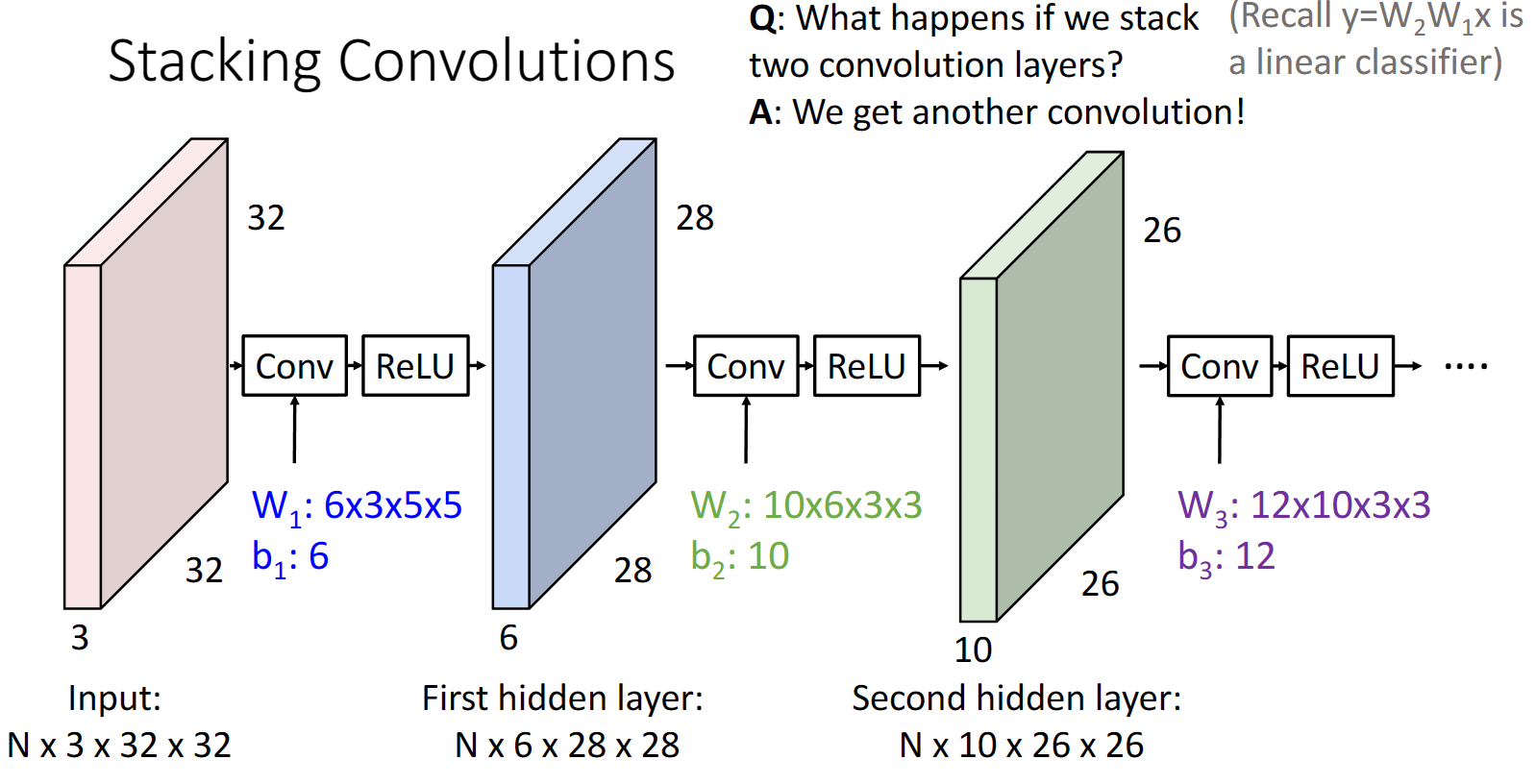
我們可以將不同的折積層進行疊加,記得注意要在折積層之後還要加入一個relu層,否則兩個折積層的連線和一個折積層毫無區別:
我們可以採用和之前一樣的視覺化方法,看看折積層實際上做了什麼:
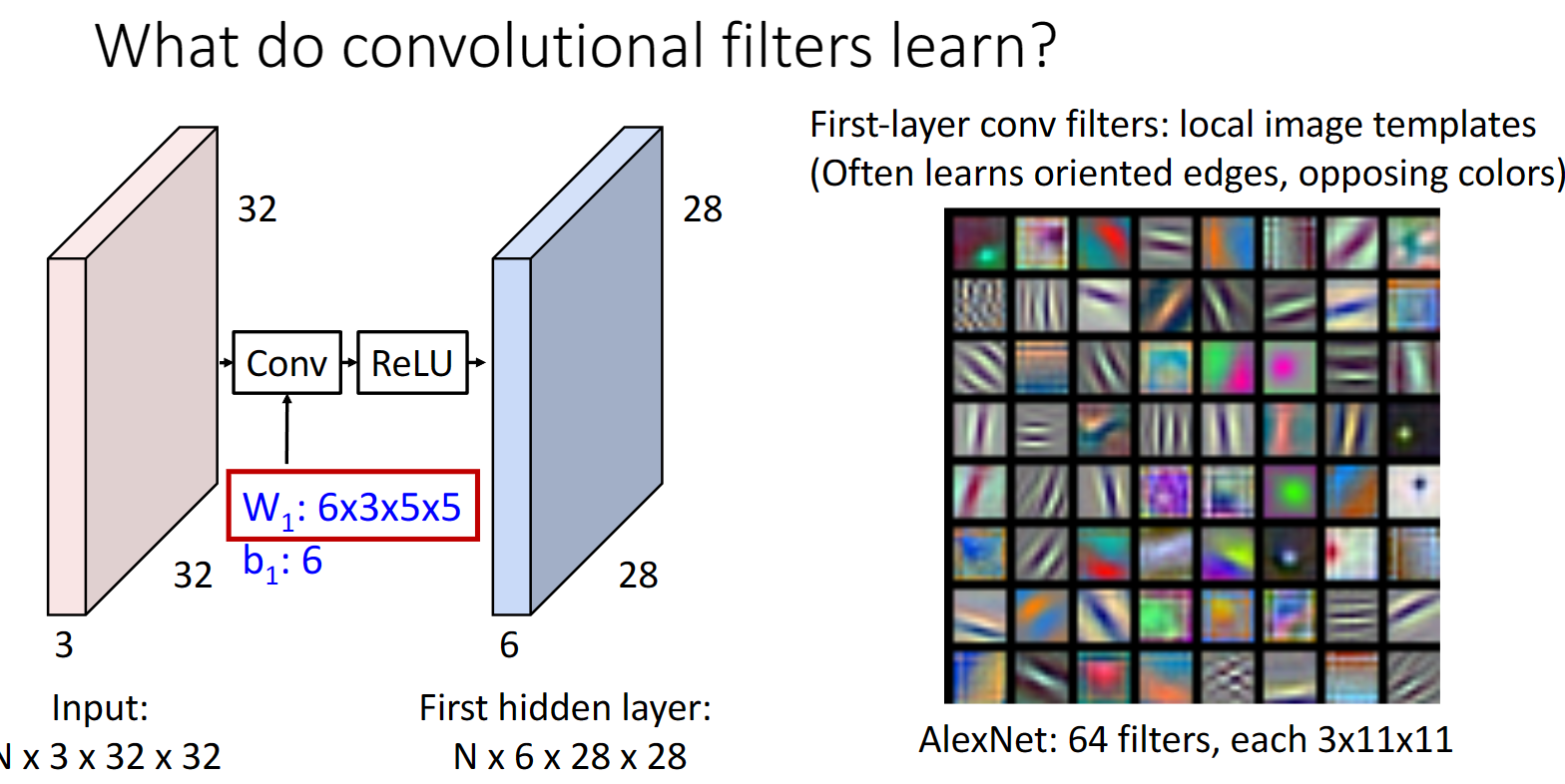
我們可以看出折積層提供的影象模板,和我們之前用線性分類器或者全連線網路得到的很不一樣,這裡的模板大多是一些邊緣或者顏色資訊,從另一個角度說,折積層其實起到了提取影象特徵的作用,我們可以把這些模板都看作影象的某種特徵
在之前我們也提到過,輸入層影象在經過折積層之後,它的大小會縮減,實際上也損失了某種影象資訊,我們不想這樣,於是引入了padding,在原本的影象周圍加上0,保證影象的維度不變:
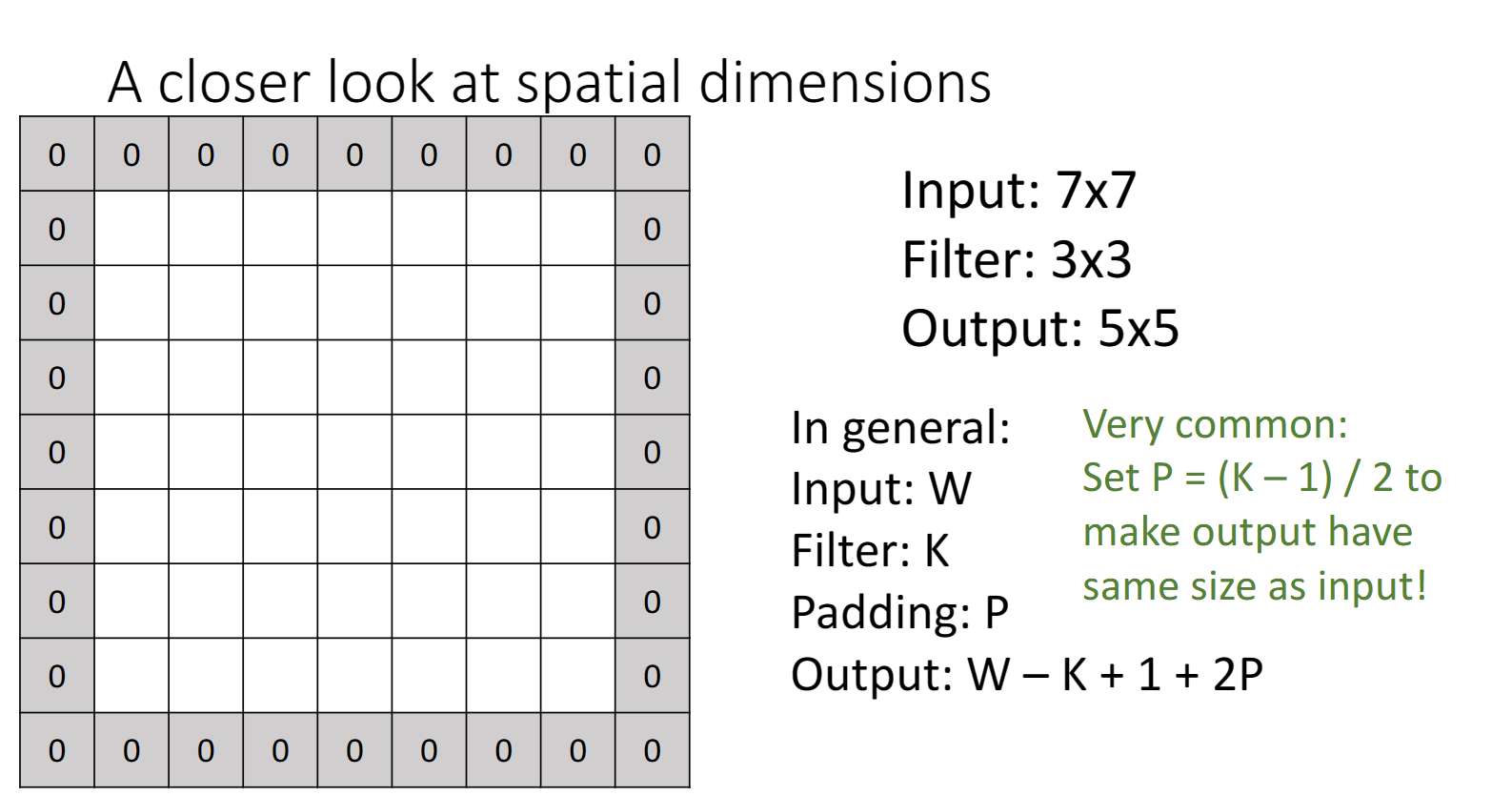
現在我們來看另一個問題:

在經過不同折積層之後,對於輸出層來說,想要去學習全域性的影象,看到全域性的影象非常困難,所以我們需要下取樣來縮小影象,便於特徵的提取,這樣我們引入了步長stride的概念,就是我們的折積核在影象上滑動時,是一次滑動stride步長:
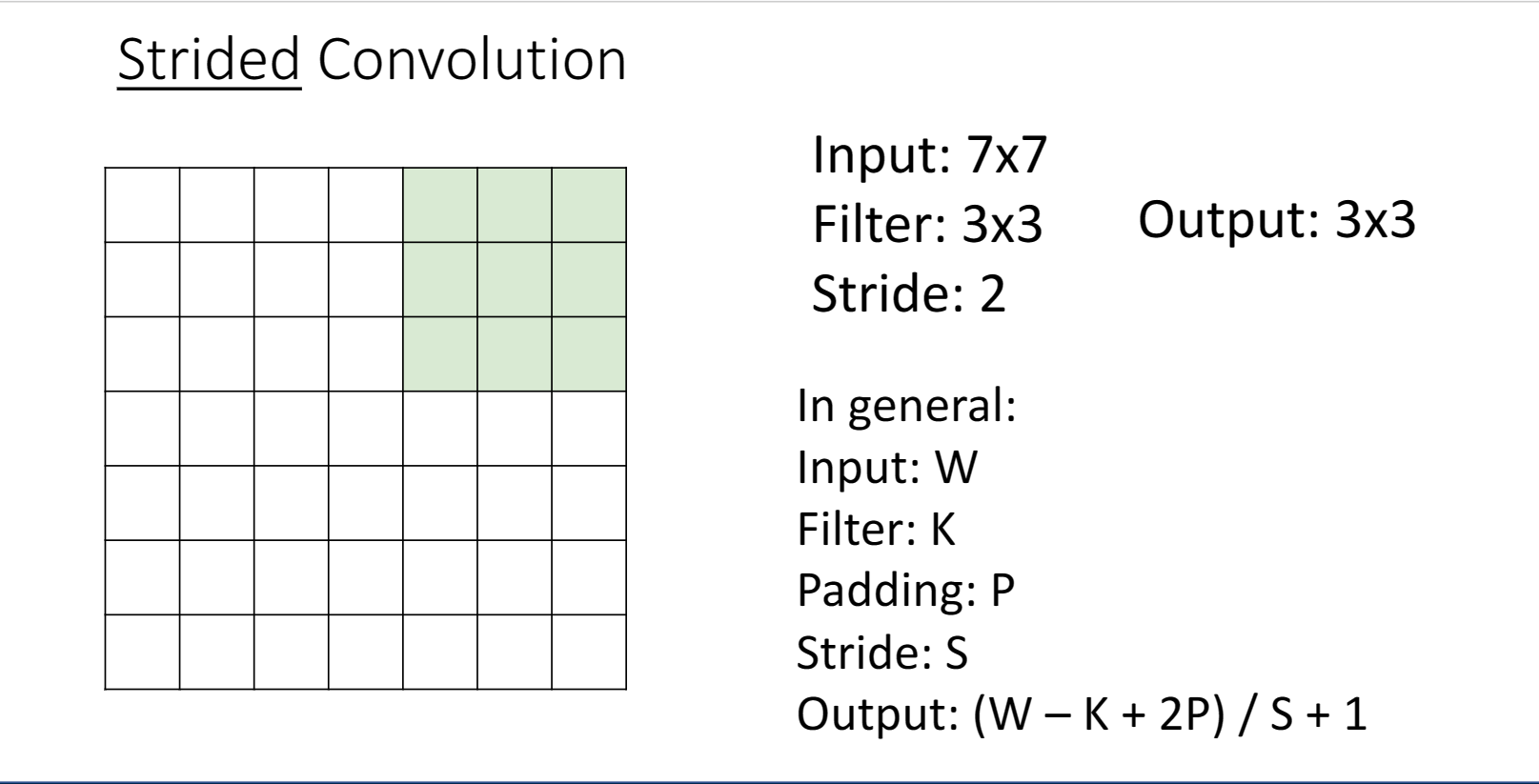
然後我們來看看關於折積層的其它資訊,比如說可學習的引數:

顯然每個filter矩陣的每個引數都是可學習的,同時也不要忘了偏置項
比如說運算次數:
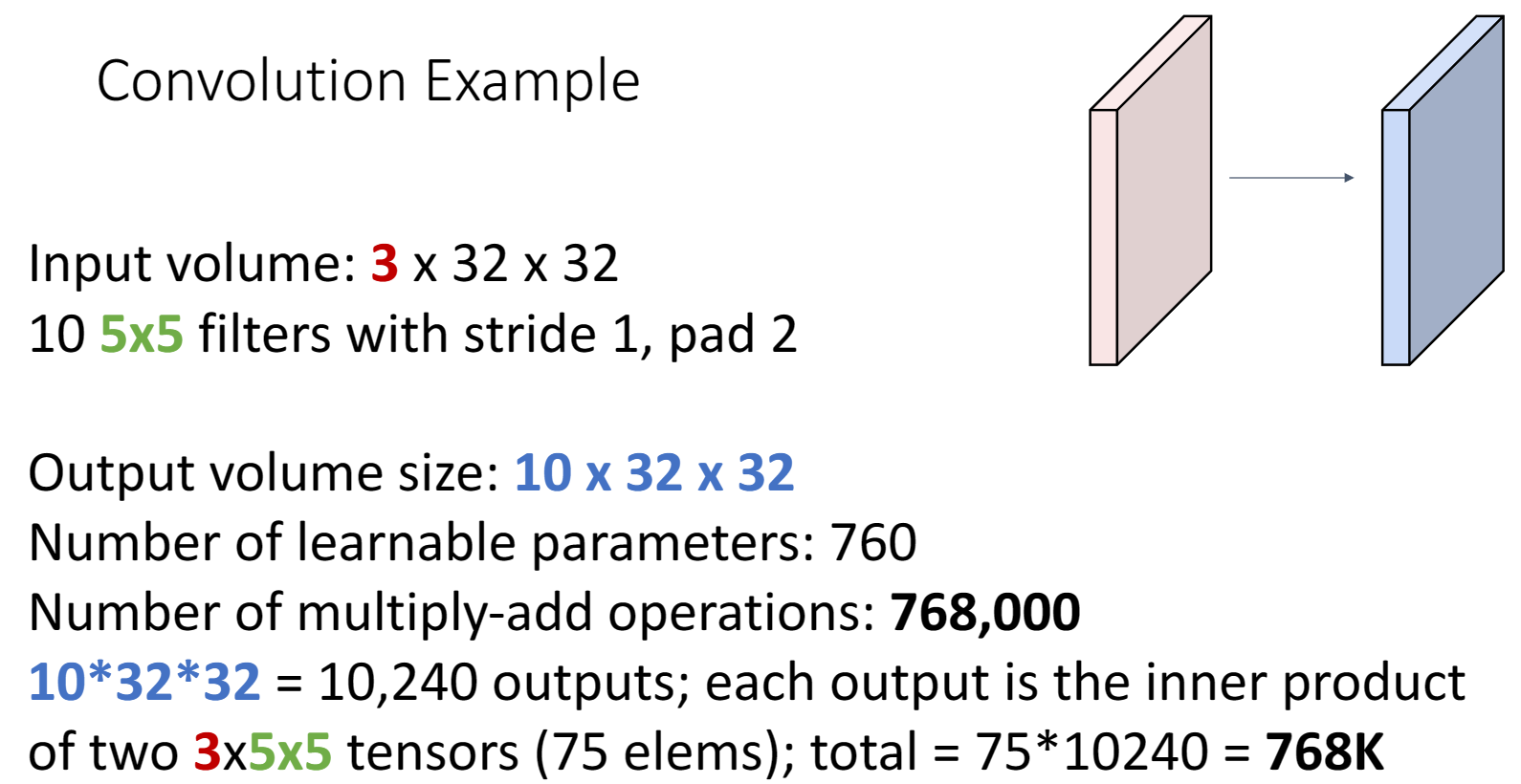
總共有10240個輸出,每個輸出都是通過點積(75次運算)得到
最後總結一些常見引數設定:

池化層
池化層也是一種下取樣的方法,可以實現影象縮小與特徵降維,常用的有平均池化與最大池化:
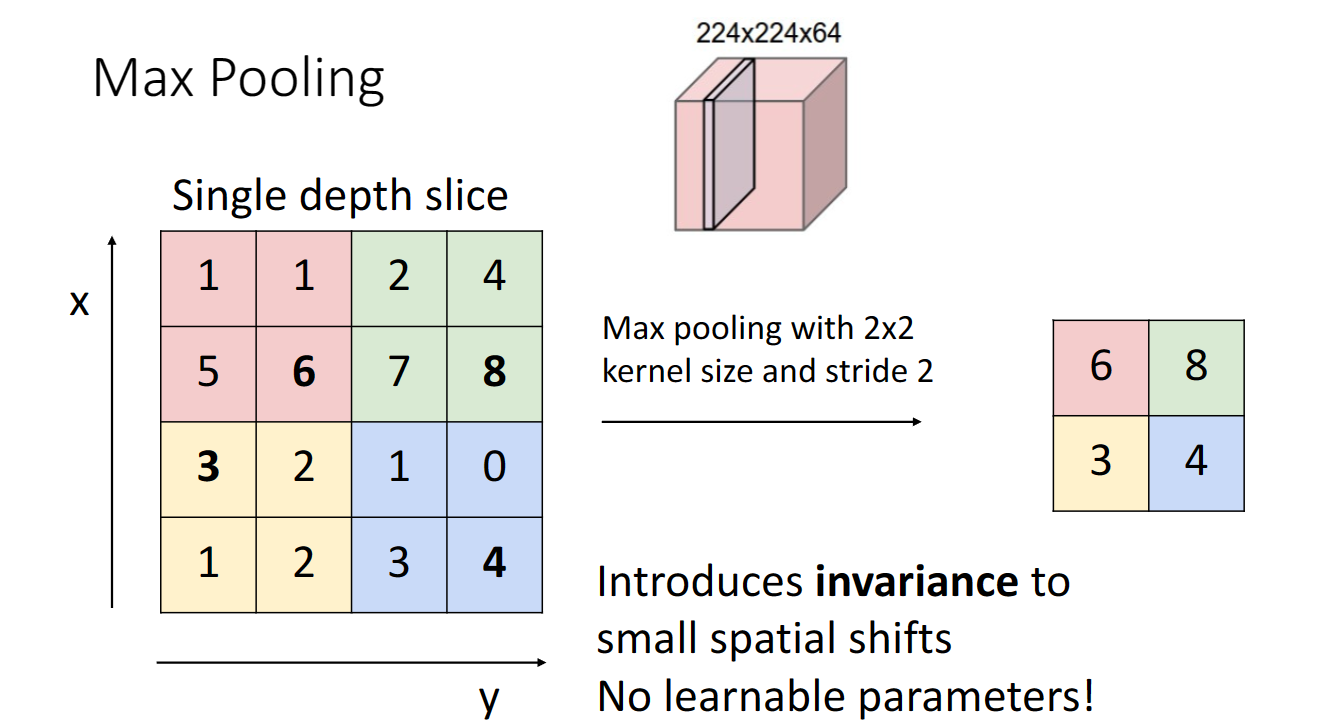
max pooling就是取對應kernel size區域裡面的最大值,同樣這裡也可以設定步長值
常用的設定如下,我們可以發現池化層是隻有超引數設定的,沒有任何可學習的引數

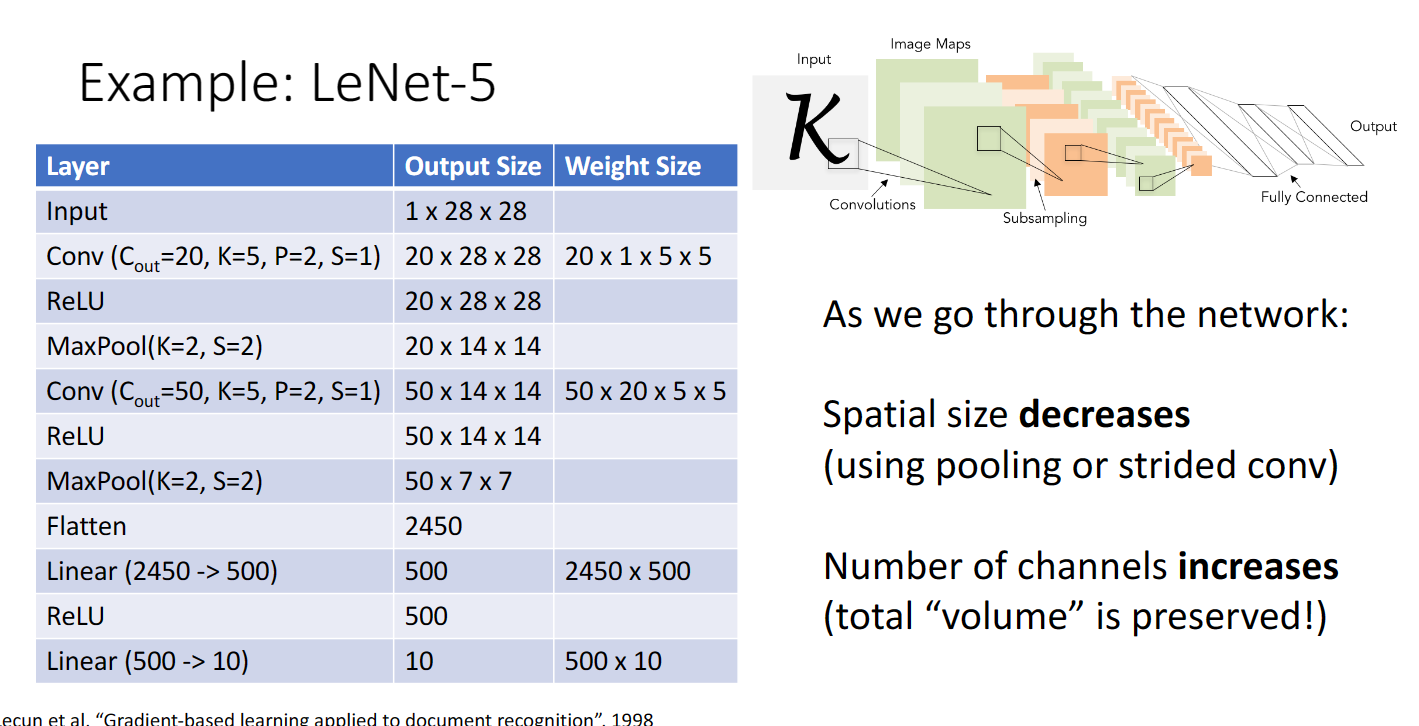
下圖是一個折積神經網路的架構,我們可以看到使用折積層與池化層,可以實現空間的降維但是通道數提升,我認為這意味著我們得到了更多更簡單但是更有用的影象特徵:
normalization
batch normalization是在2015年發現的一種可以極大地提升訓練神經網路速度的方法,可以使其快速收斂,但是小哥哥老師在課上指出,他覺得原論文的數學原理的闡述並不是很有道理