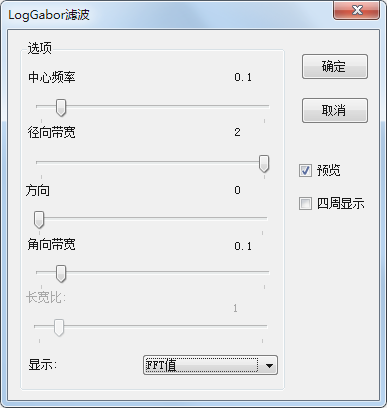
【短道速滑十一】標準的Gabor濾波器及Log_Gabor濾波器的實現、解析、速度優化及其和Halcon中gen_gabor的比較。

　　最近有朋友在研究Halcon中gen_gabor的函數，和我探討，因為我之前也沒有怎麼去關注這個函數，因此，前前後後大概也折騰了有一個星期去模擬實現這個東西，雖然最終沒有實現這個函數，但是也是有所收穫，這裡做一點總結，也算是最這個函數有個完美的收尾吧。

　　1、Gabor濾波器

　　首先總是度娘出場，關鍵詞Gabor濾波器，一大堆東西出來了，裡面最多的肯定是關於OpenCv的getGaborKernel函數，這個函數的具體程式碼如下：

/*
 Gabor filters and such. To be greatly extended to have full texture analysis.
 For the formulas and the explanation of the parameters see:
 http://en.wikipedia.org/wiki/Gabor_filter
*/
cv::Mat cv::getGaborKernel( Size ksize, double sigma, double theta,
                            double lambd, double gamma, double psi, int ktype )
{
    double sigma_x = sigma;
    double sigma_y = sigma/gamma;
    int nstds = 3;
    int xmin, xmax, ymin, ymax;
    double c = cos(theta), s = sin(theta);
    if( ksize.width > 0 )
        xmax = ksize.width/2;
    else
        xmax = cvRound(std::max(fabs(nstds*sigma_x*c), fabs(nstds*sigma_y*s)));

    if( ksize.height > 0 )
        ymax = ksize.height/2;
    else
        ymax = cvRound(std::max(fabs(nstds*sigma_x*s), fabs(nstds*sigma_y*c)));

    xmin = -xmax;
    ymin = -ymax;
    CV_Assert( ktype == CV_32F || ktype == CV_64F );
    Mat kernel(ymax - ymin + 1, xmax - xmin + 1, ktype);
    double scale = 1;
    double ex = -0.5/(sigma_x*sigma_x);
    double ey = -0.5/(sigma_y*sigma_y);
    double cscale = CV_PI*2/lambd;
    for( int y = ymin; y <= ymax; y++ )
        for( int x = xmin; x <= xmax; x++ )
        {
            double xr = x*c + y*s;
            double yr = -x*s + y*c;

            double v = scale*std::exp(ex*xr*xr + ey*yr*yr)*cos(cscale*xr + psi);
            if( ktype == CV_32F )
                kernel.at<float>(ymax - y, xmax - x) = (float)v;
            else
                kernel.at<double>(ymax - y, xmax - x) = v;
        }
    return kernel;
}

　　可以快速看出，這段程式碼僅僅是根據一些引數計算出一個折積核，具體的公式我也沒怎麼關注，裡面有個nstds 這個常數為3，這個只在使用者輸入的ksize尺寸為0的時候需要用到，感覺是和高斯核函數在半徑大於3*Sigma後其對結果的貢獻就可以忽略不計有關。 

　　這個函數生成的折積核的形狀和引數之間的關係，很多文章都有探討，這個不是本文的重點，比如下面這個連結：https://blog.csdn.net/Wslsdx/article/details/110728050

　　基本上，在空域他的形狀就是一些有間隔的白色過度條，在頻域，則基本為兩處白色亮點，如下圖所示：

       、

　　這裡用了16個濾波器組合求最大值，得到了一種特徵線條凸出的效果。 

　　當然，OpenCv的這個濾波器在一些特徵識別方面也有著很大的作用，比如斑馬線識別等等。

　　但是，測試發現這個濾波器對引數的設定極其敏感，同一個引數，一般兩個值如果只相差一點點，一般出來的效果不會有太大的區別，但是這個函數，確可能會出現極大的差異。比如波長這個引數，當為0.4和0.5的結果大相徑庭。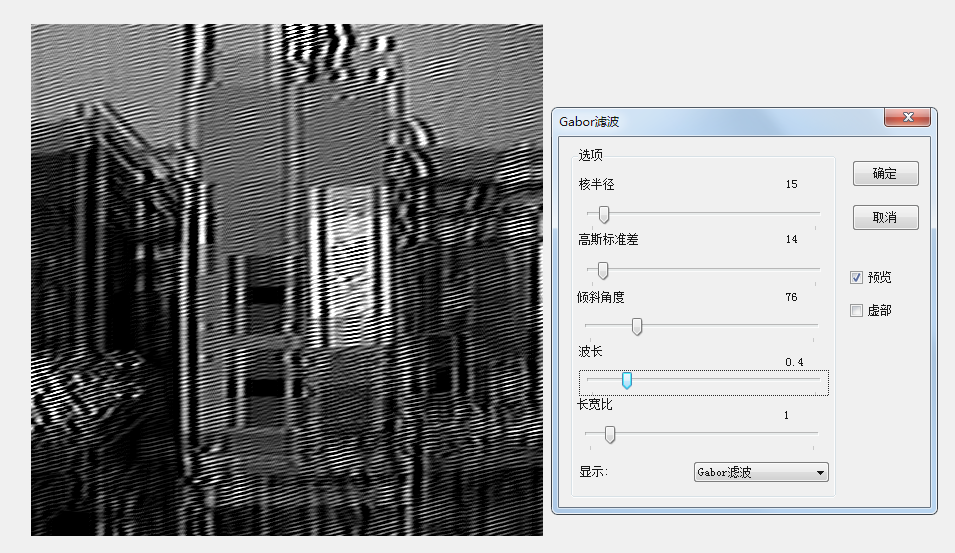  　    

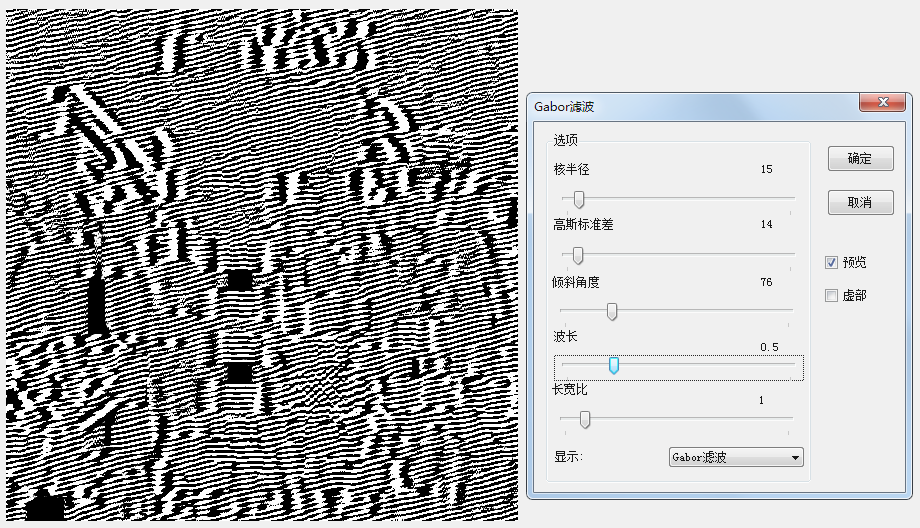
　　　　　　　　　　　　　　　　波長為0.4時的結果　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　波長為0.5時的結果

　　仔細的分析這個問題，我們會發現，這個還是由於當引數改變時，這個濾波器的權重會出現波動，一般這些折積核都需要歸一化或做相關處理，當波長為0.5時，我們會發現歸一化時，所有濾波器的和可能為負數或者很小的數，而為0.4時則較為正常。因此，出現了引數改變一點點，結果改變一大串的問題。

　　再稍微撤遠一點，當我自己實現這個函數時，我們會發現他的主要耗時還是Filter2D函數，關於這個函數，OpenCV內部是做了優化的，他會根據硬體的支援情況使用opencl/ipp等加速資源實現，速度是相當的快，而且也會對核的大小做判斷，很小的核不會使用FFT。  我這裡直接使用FFT做的實現，雖然我在進行FFT折積時做了很多優化，比如拆解為多個256*256的FFT， 比如充分利用虛部的資料等等，結果還是幹不過Opencv的速度。

　　二、LogGabor濾波器

　　拿OpenCv的Gabor濾波器和Halcon的gen_gabor相比，發現他們根本不是一回事，gen_gabor直接生成了頻域的資料，而不是生成了折積核。關於這個運算元，我們發現halcon裡的描述也不是特別的清晰，這有點不太像他的風格。

　　百度搜尋gen_gabor我們能發現的99%的資料都是halcon幫助檔案的英文原版或者是相關翻譯，基本沒有對其進行原理進行描述。可能也是因為這個運算元不是很常用的原因吧。

　　在搜尋Gabor濾波器時，也看到了一些文章講LogGabor濾波器，其中有一篇文章有提到 Log-Gabor函數並不能在空間域中得到表示式，濾波器的構造須在頻域中進行，這個和gen_gabor的描述非常相似。後面我們對其引數進行了一些分析，基本可以確定halcon的gabor應該是類似於LogGabor濾波器之類的。

　　通過搜尋LogGabor，我們得到了一下幾個比較有用的參考連結和程式碼：

　　　Python OpenCV實現Log Gabor濾波器（由LGHD描述符擴充套件） 以及 Github中一篇 PhaseCongruency/gaborconvolve.m的matlab程式碼

　　還有一個非常有用的圖片：

　　通過閱讀這幾篇文章及其配套的程式碼，我們發現這個頻域的濾波器可由Log-Radial Gaussian和Angular Gaussian組合而成，在Python那篇文章中，則有這更為明確的公式：

　　原文描述如下：

　　　　　　一個二維的L-Gaborj波器可以分解為徑向濾波器和角度濾波器兩部分，對應極座標公式為:

　　　　　　完整的Log-Gabor濾波器由這兩部分相乘得到:

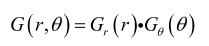
　　這個公式也和上面的圖片能完全對應。

　　在程式碼實現上，我發現無失真是Python的程式碼還是matlab的程式碼其實都是一個版本的，他們在計算有關的過程中都有一個lowpass的過程，我不清楚那個是目的是啥，也不知道哪裡的引數來源依據是什麼，但是我感覺他們不應該是我所需要的，我需要的就是上面兩個公式，結合那些參考程式碼，我們對第一個公式（徑向濾波器）的M程式碼實現如下：

WaveLength = 10;
SigmaR = 0.4;
cols = 500, rows=500;
[x,y] = meshgrid( [-cols/2:(cols/2-1)]/cols,[-rows/2:(rows/2-1)]/rows);
radius = sqrt(x.^2 + y.^2);       
Frequency = 1.0 / WaveLength;                  % 頻率等於波長的導數
logGabor = exp((-(log(radius / Frequency)).^2) / (2 * SigmaR * SigmaR));  % log gabor函數的傳遞函數表示式
imshow(logGabor,[])

　　對第二個公式的實現程式碼如下：

Angle = 45 / 180 *3.1415926;
SigmaA = 0.4;
cols = 500, rows=500;
[x,y] = meshgrid( [-cols/2:(cols/2-1)]/cols,[-rows/2:(rows/2-1)]/rows);
theta = atan2(-y,x);              
sintheta = sin(theta);
costheta = cos(theta);
ds = sintheta * cos(Angle) - costheta * sin(Angle);    
dc = costheta * cos(Angle) + sintheta * sin(Angle);     
dtheta = atan2(abs(ds),abs(dc));                           
spread = exp((-dtheta.^2) / (2 * SigmaA * SigmaA));      
imshow(spread,[])

　　當將兩者組合起來後，即產生如下的程式碼：

WaveLength = 10;
SigmaR = 0.4;
Angle = 45 / 180 *3.1415926;
SigmaA = 0.4;
cols = 500, rows=500;
[x,y] = meshgrid( [-cols/2:(cols/2-1)]/cols,[-rows/2:(rows/2-1)]/rows);
radius = sqrt(x.^2 + y.^2);  
Frequency = 1.0 / WaveLength;                  % 頻率等於波長的導數
logGabor = exp((-(log(radius / Frequency)).^2) / (2 * SigmaR * SigmaR));  % log gabor函數的傳遞函數表示式
theta = atan2(-y,x);              
sintheta = sin(theta);
costheta = cos(theta);
ds = sintheta * cos(Angle) - costheta * sin(Angle);    
dc = costheta * cos(Angle) + sintheta * sin(Angle);     
dtheta = atan2(abs(ds),abs(dc));                           
spread = exp((-dtheta.^2) / (2 * SigmaA * SigmaA));      
imshow(logGabor .* spread,[])

　　三段程式碼產生的影象依次如下所示：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　WaveLength = 10，SigmaR = 0.4，Angle = 45 / 180 *3.1415926， SigmaA = 0.4;

　　通過改變引數可以獲得不同的效果，比如，WaveLength = 5，SigmaR = 0.05，Angle = 30 / 180 *3.1415926， SigmaA = 0.3時的效果如下：

　　注意到，相比於原始的程式碼，我們在計算dtheta時，稍微做了修改，這是因為，頻域的資料一般是要求堆成的，而原始的角向濾波器是非對稱的，因此，我們改成了atan2(abs(ds),abs(dc));

　　這個生成的過程裡有很多浮點的計算，而且有幾個複雜度比較高的函數，因此，計算還是有所耗時的。 

　　我們來和halcon的gen_gabor的引數做下比較：

　　　　　　　　gen_gabor( : ImageFilter : Angle, Frequency, Bandwidth, Orientation, Norm, Mode, Width, Height : )

　　後面Norm, Mode, Width, Height 這四個引數不用管它，我們主要看看前面四個引數。 

　　注意到我們剛才的程式碼裡也提供了四個可選的引數，即WaveLength，SigmaR，Angle， SigmaA，那他們之間有麼有什麼對應的關係呢。 

　　通過多次比較和測試，我們可以定性的確定如下聯絡：

　　1、gen_gabor裡的Orientation和我的LogGabor裡的Angle基本是一個意思，這個可以從Orientation的範圍可以看到，就是個角度範圍：

　　　　　Orientation (input_control) real → (real)
　　　　　　　　Angle of the principal orientation，Suggested values: 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.14

　   2、gen_gabor的Bandwidth和LogGabor的SigmaR的趨勢基本是一致的。

       3、gen_gabor的Frequency和LogGabor的WaveLength的趨勢基本是相反的，但是WaveLength本身就是Frenquency的倒數，都是會隨著Frequency的變小，頻域的有效部分想中心收縮。

       4、gen_gabor的Angle和LogGabor的SigmaA的趨勢基本是相反的。

　　也就是說這4個引數基本上都存在一一對應的關係，只是說我們無法確認他們之間的絕對值之間的聯絡，畢竟halcon裡也沒有提供具體的計算式，只要稍微某個地方有些取值不同，就會造成不同的結果。 

　　由於loggabor提供的已經是頻域的資料了，因此，後續的計算就比較簡單了，因為頻域的乘法就相當於於時域的折積，因此，直接把某個影象的頻域資料乘以這個LogGabor資料就可以了。

       但是，這就要求LogGabor的資料維度必須和影象是一樣大小的，其實這個有個隱藏的問題，即邊緣問題，因為折積對於邊緣一般來說是需要擴充套件的，否則會遇到一些小小意料之外的問題。 

　　做了一個簡單的比較，當gen_gabor和LogGabor濾波器的視覺化圖基本類似時，大部分情況兩者之間的效果似乎方向是一致的。 

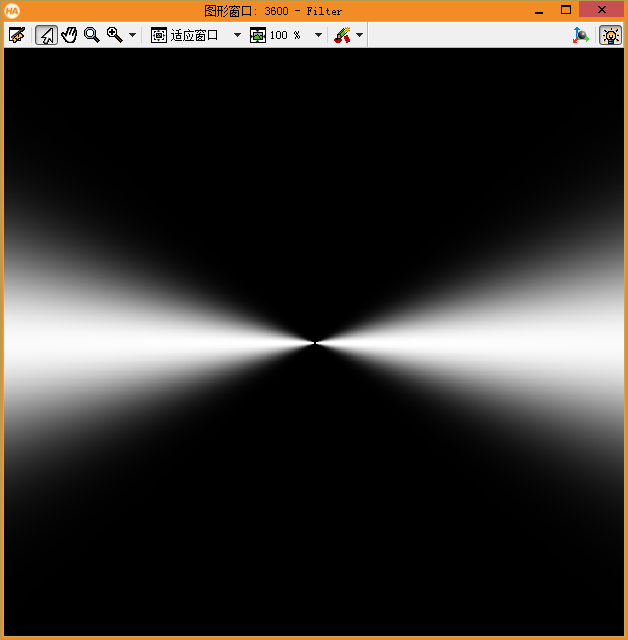
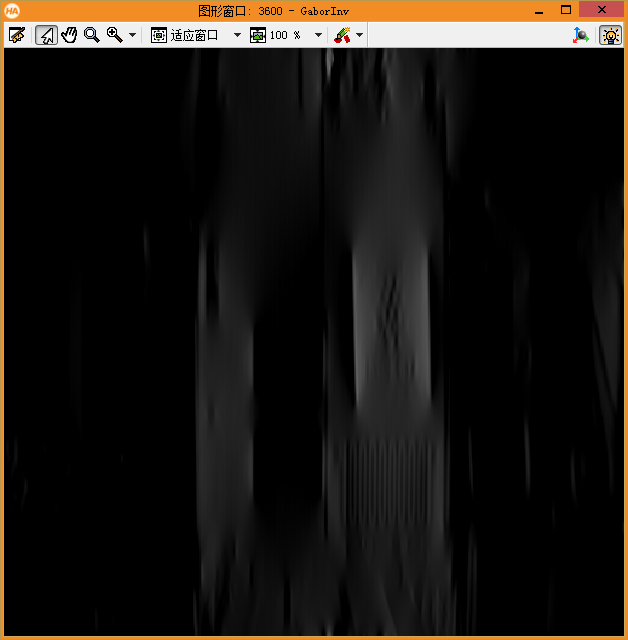
　　　　　　　　　　　　halcon的gen_gabor視覺化結果　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　對應的濾波器輸出