一、Caesar_base

題目資訊

s = "HIJKLMNOPQRSTUVWXYZABCDEFGhijklmnopqrstuvwxyzabcdefg0123456789+/"    #碼錶

def My_base64_encode(inputs):
	bin_str = []
	for i in inputs:
		x = str(bin(ord(i))).replace('0b', '')
		bin_str.append('{:0>8}'.format(x))
	#print(bin_str)
	outputs = ""
	nums = 0
	while bin_str:
		temp_list = bin_str[:3]
		if(len(temp_list) != 3):
			nums = 3 - len(temp_list)
			while len(temp_list) < 3:
				temp_list += ['0' * 8]
		temp_str = "".join(temp_list)
		#print(temp_str)
		temp_str_list = []
		for i in range(0,4):
			temp_str_list.append(int(temp_str[i*6:(i+1)*6],2))
		#print(temp_str_list)
		if nums:
			temp_str_list = temp_str_list[0:4 - nums]
			
		for i in temp_str_list:
			outputs += s[i]
		bin_str = bin_str[3:]
	outputs += nums * '='
	print("Encrypted String:\n%s "%outputs)

print("-------input 'ys' to encode-------")	

sr = input("Please input!\n")
if(sr == "ys"):
	input_str = input("Please enter a string that needs to be encrypted: \n") 
	My_base64_encode(input_str)            
  

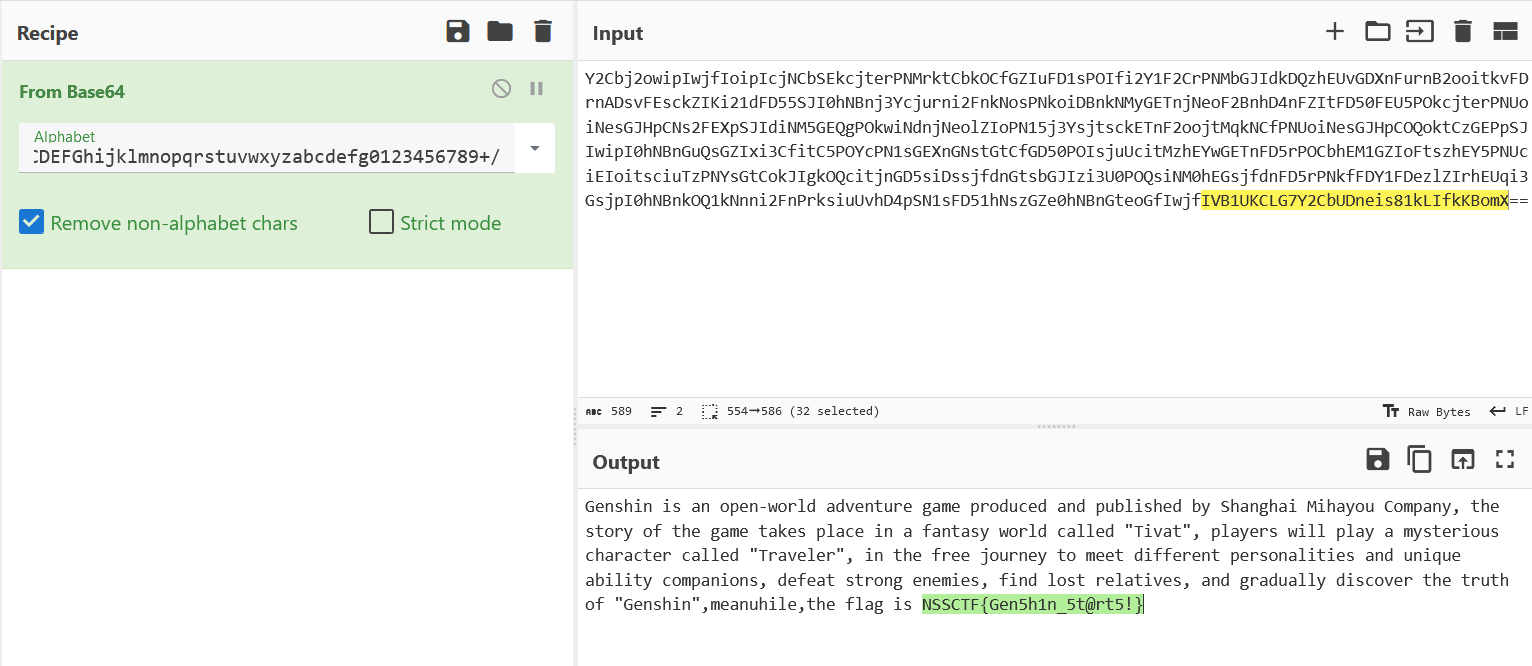
根據第一行新表base64解碼即可

二、EasyRSA

題目附件

import libnum  
  
p=libnum.generate_prime(1024)  
q=libnum.generate_prime(1024)  
e=65537  
m="NSSCTF{*******************}"  
m=libnum.s2n(m)  
n=p*q  
phi_n=(p-1)*(q-1)  
d=libnum.invmod(e,phi_n)  
c=pow(m,e,n)  
  
print("p=",p)  
print("q=",q)    
print ("e=",e)  
print ("c=",c)

#p= 122912801126049869009003839542545176400185213365268209105714006257803073428638629824801261702125287814910668428403367391355051987389837804474055637991864563803834741161217607848968821280710324766558457056004037592628178078680121173634128054936108782807954132605887275556228703383455969903056759874047110115433
#q= 120790113700754477830062212762518406876786376726996249661848284428829412089402183812692045970711341815805796005449714738748110749559462448861357011272792817313060401380148108517705435100103533857957024851181447994572972501120774586405811257420853542417275740953525627232008812587423053626515513859653865873671
#e= 65537
#c= 7094224488947659163318199615533819770556597977720767621640224798887506152292861133457571683713587909779712343346370719403811813233693263526316785431883833118583425528830238629831001255198236686372518770451273159769779374149881346761523688131115323441973953523582174059584087249568245044443295176738493785560215046375056269378223045128094953923926250055718405799885041115025529297362914403732661935017257507786348635366480744933193471899621592092711962814949533564454932121056035003021428158830645604347966849572981124877683317022116903132719663958775850982016292384237647664448371811915879714093710876989697939277005

基礎RSA

exp:

import gmpy2
from Crypto.Util.number import long_to_bytes
p = 122912801126049869009003839542545176400185213365268209105714006257803073428638629824801261702125287814910668428403367391355051987389837804474055637991864563803834741161217607848968821280710324766558457056004037592628178078680121173634128054936108782807954132605887275556228703383455969903056759874047110115433
q = 120790113700754477830062212762518406876786376726996249661848284428829412089402183812692045970711341815805796005449714738748110749559462448861357011272792817313060401380148108517705435100103533857957024851181447994572972501120774586405811257420853542417275740953525627232008812587423053626515513859653865873671
c = 7094224488947659163318199615533819770556597977720767621640224798887506152292861133457571683713587909779712343346370719403811813233693263526316785431883833118583425528830238629831001255198236686372518770451273159769779374149881346761523688131115323441973953523582174059584087249568245044443295176738493785560215046375056269378223045128094953923926250055718405799885041115025529297362914403732661935017257507786348635366480744933193471899621592092711962814949533564454932121056035003021428158830645604347966849572981124877683317022116903132719663958775850982016292384237647664448371811915879714093710876989697939277005

phi = (p-1) * (q-1)
e = 65537
n = p * q
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print('