1 Laplacian 運算元
給定無向圖\(G=(V, E)\),我們在上一篇部落格《譜圖論:Laplacian二次型和Markov轉移運算元》中介紹了其對應的Laplacian二次型:
\[\mathcal{E}[f]=\frac{1}{2} \cdot \mathbb{E}_{u \sim v}\left[(f(u)-f(v))^2\right]
\]
這裡\(f: V\rightarrow \mathbb{R}\)為圖的頂點標籤,\(u\sim v\)表示服從均勻分佈的隨機無向邊\((u, v)\in E\)。直觀地理解,Laplacian二次型刻畫了圖的「能量」(energy)。\(\mathcal{E}[f]\)的值越小,也就意味著\(f\)更加「光滑」(smooth),即其值不會沿著邊變化得太劇烈。
事實上,我們可以做進一步地等價變換:
\[\begin{aligned}
\mathcal{E}[f] &=\frac{1}{2} \cdot \mathbb{E}_{u \sim v}\left[(f(u)-f(v))^2\right]\\
&= \langle f, f \rangle - \mathbb{E}_{u\sim v}\left[f(u)f(v)\right]\\
&= \langle f, f \rangle - \langle f, Kf \rangle\\
&= \langle f, If - Kf \rangle \\
&= \langle f, (I - K) f \rangle
\end{aligned}
\]
這\(K\)為我們在上一篇部落格中提到的MarKov轉移運算元,它滿足:\((K f)(u)=\mathbb{E}_{v \sim u}[f(v)]\)。
對於最後一個等式而言,我們稱運算元
\[L = I - K
\]
為圖\(G\)的 (歸一化)Laplacian運算元。
注 對於\(d\)-正則圖\(G\)而言,我們有
\[L = I - \frac{1}{d} A = \frac{1}{d}(dI - A)
\]
這裡\(A\)為\(G\)的鄰接矩陣,\(dI - A\)被稱為非歸一化Laplacian運算元,或直接被簡稱為Laplacian運算元。
和\(K\)一樣,\(L\)也是定義在函數空間\(\mathcal{F}=\{f: V \rightarrow \mathbb{R}\}\)上的線性運算元,按照以下規則將\(f\in \mathcal{F}\)對映到\(Lf\in \mathcal{F}\),滿足
\[Lf(u) = f(u) - \mathbb{E}_{v\sim u}[f(v)],
\]
通過研究\(L\),我們就能把握Laplacian二次型\(\mathcal{E}[f] = \langle f, Lf \rangle\)的特性,從而把握圖\(G\)的特性,這是譜圖理論中至關重要的一點。
接下來再來看我們熟悉的那個示性函數例子。
例 設圖頂點的子集\(S\subseteq V\), 0-1示性函數\(f=\mathbb{I}_S\)用於指示頂點是否在集合\(S\)中,即:
\[f(u)=\left\{\begin{array}{lll}
1 & \text { if } & u \in S \\
0 & \text { if } & u \notin S
\end{array}\right.
\]
則我們有:
\[\begin{aligned}
& \langle f, Lf \rangle = \mathbb{E}[f] = \text{Pr}_{u\sim v}[u\in S, v\notin S]\\
& \langle f, f\rangle = \mathbb{E}_{u\sim \pi}[f(u)^2] = \text{Pr}_{u\sim \pi}[u\in S] = \text{vol}(S)
\end{aligned}
\]
直觀地理解,這裡\(\text{Pr}_{u\sim v}[u\in S, v\notin S]\)表示「伸出」\(S\)的邊佔總邊數的比例;\(\text{vol}(S)\)表示\(S\)的「體積」。則上述兩式的比值
\[\begin{aligned}
\frac{\langle f, Lf\rangle}{\langle f, f \rangle} &= \text{Pr}_{u\sim v}\left[v\notin S\mid u \in S \right]\\
&= \text{Pr}\left[ \underbrace{\text{pick a random } u\in S}_{\text{proportional to the degree}}\text{, do }\ 1 \text{ step, that you get out of } S \right] \\
& \in \left[0, 1\right]
\end{aligned}
\]
表示從集合\(S\)中的「逃出」概率。我們將這個比值稱為\(S\)的電導(conductance)(我們在部落格《圖資料探勘:重疊和非重疊社群檢測演演算法》中介紹過,當時是用來衡量社群劃分的質量,這個值越小說明劃分得越好),用\(\Phi[S]\)表示。
2 再論Laplacian二次型的極值
有了\(L\),那麼最小化/最大化\(\mathcal{E}[f]\)的問題就可以進行進一步的研究了。考慮下列優化問題:
\[\begin{aligned}
& \max \quad \mathcal{E}[f] = \langle f, Lf\rangle = \underbrace{\frac{1}{2}\mathbb{E}_{u\sim v}\left[\left(f(u) - f(v)\right)^2\right]}_{\text{continous func. } f: \space\mathbb{R}^n\rightarrow \mathbb{R}}\\
& \text{s.t.} \underbrace{\quad \lVert f \rVert^2_2 = \langle f, f\rangle = \mathbb{E}_{u\sim\pi}[f(u)^2] = 1}_{\text{compat set}, \text{ ellipsoid in } \mathbb{R}^n} \quad (\Leftrightarrow\text{Var}[f] = 1)
\end{aligned}
\]
存在一個極大值點\(\varphi: V\rightarrow \mathbb{R}\),它滿足:
\[L \varphi=\lambda \varphi \quad \text { for some } \lambda \in \mathbb{R},
\]
也即\(L\varphi \parallel \varphi\)。此外,該極大點也可以被有效地找到。
推論
\[\mathcal{E}[\varphi] = \langle \varphi, L\varphi\rangle = \langle \varphi, \lambda \varphi \rangle = \lambda \langle \varphi, \varphi \rangle = \lambda \in \left[0, 2\right]
\]
事實
\[\begin{aligned}
& \mathbb{E}[\varphi] = \mathbb{E}_{u\sim \pi}\left[\varphi(u)\right] = \mathbb{E}_{u\sim \pi}\left[\varphi(u) \cdot 1\right] = 0 \Leftrightarrow \langle \varphi, \mathbb{1} \rangle = 0 \Leftrightarrow \varphi \perp \mathbf{1}\\
& \text{Var}[\varphi] = 1
\end{aligned}
\]
下面我們來證明為什麼\(\mathcal{E}[f]\)的極大值點\(\varphi\)滿足\(L\varphi \parallel \varphi\)。
證明 我們採用反證法,即假設極大值點\(\varphi\)滿足\(L\varphi \nparallel \varphi\),如下圖所示:
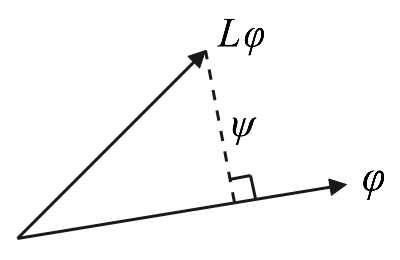
由於\(L\varphi \nparallel \varphi\),那麼我們可以現在\(L\varphi\)與\(\varphi\)之間的垂線方向上取\(f = \varphi + \varepsilon \psi\)(\(\varepsilon\neq 0\)是一個很小的數,\(\psi\)為單位向量),根據勾股定理有\(\lVert f \rVert^2_2 = 1 + \epsilon^2\)。則:
\[\begin{aligned}
\mathcal{E}[f] = \langle f, Lf \rangle &\overset{(1)}{=} \langle \varphi + \varepsilon \psi, L\varphi + L\varepsilon \psi \rangle \\
& \overset{(2)}{=} \langle \varphi, L \varphi \rangle + \underbrace{\varepsilon \langle \phi, L \psi \rangle + \varepsilon \langle \psi, L \varphi \rangle}_{L \text{ is self-adjoint}} + \varepsilon^2 \langle \psi, L \psi \rangle\\
& \overset{(3)}{=} \langle \varphi, L \varphi \rangle + \underbrace{2\varepsilon \langle \psi, L \varphi \rangle}_{>0} + \mathcal{O}(\epsilon^2) \\
& > \langle \varphi, L \varphi \rangle
\end{aligned}
\]
(其中等式\((3)\)用到了自伴運算元的定義)而這與\(\varphi\)為極大值點相矛盾。因此,\(\mathcal{E}[f]\)的極大值點\(\varphi\)滿足\(L\varphi \parallel \varphi\)。
3 Laplacian運算元的譜性質
在上一小節,我們已經證明了\(\varphi\)是一個極大值點。現在我們不採用\(\varphi\)及所有與\(\varphi\)平行的解,而將解限制在與\(\varphi\)相正交的子空間中。這樣,優化問題就變為了:
\[\text{Max } \underbrace{\langle f, Lf \rangle}_{\text{continous func. }} \quad \text{s.t.} \underbrace{\lVert f \rVert^2_2 = \langle f, f \rangle = 1}_{\text{compat set}},\quad f\perp \varphi
\]
求解該優化問題可以採用與之前相同的思路,也即存在極大值點\(\varphi^{\prime}\)滿足:
\[L \varphi^{\prime}=\lambda^{\prime} \varphi^{\prime} \quad \text { for some } \lambda^{\prime} \leqslant \lambda,\text{and } \mathbb{E}[\varphi^{\prime}] = 0 (\Leftrightarrow \langle \varphi^{\prime}, \mathbf{1} \rangle = 0)
\]
這裡\(\lambda^{\prime} < \lambda\)的原因是\(\lambda\)已經對應了極大值點,而我們新增了新的約束使\(f\nparallel \varphi\),故這裡\(\lambda^{\prime}\)對應的是第二大的極值點。
重複這個步驟,不斷尋找第3大,第\(4\)大……的極大值點,並使其與之前找到的所有極大值點正交,直到找到最後一個(第\(n\)大的)極大值點。在這個過程中得到的極大值點都會\(\perp\)於\(\mathbf{1}\)(\(\mathbf{1}\)為全1向量),而最後一個極大值點即為所剩的\(\mathbf{1}\)向量本身,此時有
\[L\mathbf{1}=0
\]
由此可見最後一個特徵值(最小的特徵值)為0。
通過上面所述的步驟,我們可以找到Laplacian運算元的\(n\)個相互正交的規範化特徵向量(範數為1)及其對應的特徵值。而這事實上和我們線上性代數課程中所學過的譜定理密切相關。
譜定理 若\(T\)為一個實向量空間\(V\)上的自伴運算元,則\(V\)有一個由\(T\)的特徵向量組成的規範正交基(orthonormal basis)\(\varphi_1, \varphi_2, \cdots, \varphi_{n}\),每個特徵向量分別對應於實特徵值\(\lambda_1, \lambda_2, \cdots, \lambda_{n}\)。
我們前面證明過Markov轉移運算元\(K\)是自伴的,則\(L = I - K\)也是自伴的(事實上,又由於\(\langle f, Lf \rangle \geqslant 0\),\(L\)還是半正定的)。於是,關於圖\(G\)的Laplacian運算元就有以下定理:
定理 給定\(G\)及其Laplacian運算元\(L\),則存在規範正交基(函數)\(\mathbf{1} \equiv \varphi_1, \varphi_2, \cdots, \varphi_{n}\)及實數$0=\lambda_1 \leqslant \lambda_2\leqslant \cdots \leqslant \lambda_{n} \leqslant 2 $滿足:
\[L\varphi_i = \lambda_i \varphi_i
\]
我們將\(\lambda_2\)和更廣泛的\(\lambda_k\)(\(k\)為一個較小的值)稱為低頻(low-frequency) 特徵值,而將\(\lambda_n\)稱為高頻(high-frequency) 特徵值。
事實上,除了討論Laplacian運算元\(L\)之外,我們也可以討論Markov轉移運算元\(K\)的特徵向量及特徵值。由\(L = I - K\),我們有
\[K \varphi_i = (I - L) \varphi_i = I \varphi_i - L\varphi_i = \varphi_i - \lambda_i \varphi_i = (1 - \lambda_i) \varphi_i,
\]
則\(K\)擁有特徵向量\(\varphi_i\)及其相伴的特徵值 \(\kappa_i = 1 - \lambda_i\),且\(-1\leqslant \kappa_{n}\leqslant\cdots\leqslant \kappa_2 \leqslant \kappa_1 = 1\)。
定義 給定\(f: V\rightarrow \mathbb{R}\)和正交基\(\varphi_1, \varphi_2, \cdots \varphi_{n}\),那麼\(f\)能夠唯一地表示為\(\varphi_i\)的一個線性組合:
\[f = \hat{f}(1) \varphi_1 + \hat{f}(2) \varphi_2 + \cdots \hat{f}(n) \varphi_{n},\quad \hat{f}(i)\in \mathbb{R}
\]
這個性質會為我們帶來許多新的結論。
命題 將\(L\)應用於\(f\),就得到了:
\[Lf = \underbrace{\lambda_1 \hat{f}(1) \varphi_1}_{0} + \lambda_2 \hat{f}(2) \varphi_2 + \cdots + \lambda_{n} \hat{f}(n) \varphi_{n},
\]
可以看到,\(L\)應用於\(f\)可以轉換為分別去應用於正交基。為了方便,我們常常會使用如下所示的記號:
\[\widehat{Lf}(i) = \lambda_i \hat{f}(i)
\]
此外,我們也可以使用規範正交基來簡化我們內積和範數的表示。
命題 給定另一個函數
\[g = \hat{g}(1)\varphi_1 + \cdots + \hat{g}(n)\varphi_{n},
\]
則\(f\)和\(g\)的內積
\[\langle f, g\rangle = \sum_{i, j}\hat{f}(i)\hat{g}(j)\langle \varphi_i, \varphi_j \rangle = \sum_{1\leqslant i \leqslant n}\hat{f}(i)\cdot \hat{g}(i)
\]
推論
根據內積我們可以誘匯出範數
\[\lVert f \rVert^2_2 = \langle f, f\rangle = \sum_{1\leqslant i \leqslant n}\hat{f}(i)^2,
\]
\(f\)的均值可表示為:
\[\mathbb{E[f]}=\mathbb{E}_{u\sim \pi}[f(u)] = \langle f, \mathbf{1}\rangle=\langle f, \varphi_1 \rangle = \widehat{f}(1)
\]
可以看到,\(f\)沿規範正交基的展開式中的第一項就是均值乘單位向量:
\[f = \underbrace{\hat{f}(1)}_{\mathbb{E}[f]} \underbrace{\varphi_1}_{\mathbf{1}} + \hat{f}(2) \varphi_2 + \cdots \hat{f}(n) \varphi_{n}, \quad \hat{f}(i) \in \mathbb{R},
\]
\(f\)的方差可表示為:
\[\begin{aligned}
\text{Var}[f] & = \mathbb{E}[f^2] - \mathbb{E}[f]^2 \\
& = \sum_{1\leqslant i \leqslant n} \left[\hat{f}(i)^2\right] - \hat{f}(1)^2 \\
&= \sum_{1< i \leqslant n} \hat{f}(i)^2
\end{aligned}
\]
(注意第\(1\)項\(\hat{f}(1)^2 - \hat{f}(1)^2\)抵消掉了)
Laplacian二次型\(\mathcal{E}[f]\)可表示為:
\[\begin{aligned}
\mathcal{E}[f] &= \langle f, Lf \rangle \\
&= \sum_{i, j}\lambda_i \hat{f}(i)\hat{f}(j)\langle \varphi_i, \varphi_j \rangle\\
&= \sum_{1 < i\leqslant n}\lambda_i \hat{f}(i)^2
\end{aligned}
\]
(注意第\(1\)項由於\(\lambda_1=0\)就消失了)
參考
[1] CMU 15-751: TCS Toolkit
[2] Bilibili: CMU電腦科學理論(完結)—你值得擁有的數學和計算機課)
[3] Spielman D. Spectral graph theory[J]. Combinatorial scientific computing, 2012, 18: 18.
[4] Axler S. Linear algebra done right[M]. springer publication, 2015.
