【演演算法】萬聖節前夕的迷宮挑戰

這一天陽光和煦，小悅將搗蛋的侄子小明送回家後，緊繃的神經終於得以放鬆。在過去的一週裡，小悅以無比的耐心和細心照顧著小明，同時也不忘在程式設計的道路上引領他邁出第一步。

萬聖節前夕的一天，書房中的陳設在陽光下顯得莊重而溫暖，小悅正專心致志地處理著手頭的工作。突然，一封郵件如不速之客般打破了這份寧靜。郵件標題簡短，僅以「隨機迷宮-最短路徑」幾個字概括，而內容更像是一個簡單的影象附件，幾個由字元「W」和「.」組成的3x3或6x6網格。這個迷宮的難題在於，迷宮的面積是不固定的，並且一旦走到邊緣，就會被迫停滯不前。

小悅看到這封郵件後，臉上充滿了驚奇。這封郵件的來源不明，而顯然作者也沒想到郵件會輾轉發到她的郵箱。但小悅是一個喜歡接受挑戰的人，她決心找到這個迷宮的最短路徑。

雖然小悅經常面對各種解謎挑戰，但這個迷宮的難度對她來說確實不小。迷宮的起點是二維陣列的(0,0)，而終點是(5,5)。她可以按上下左右四個方向移動，但每一步只能移動一格。此外，一旦她走到了迷宮的邊緣，她就不能再繼續前進。這也就意味著她需要找到一條從起點到終點的不重複路徑，而且不能通過迷宮的邊緣。

小悅輕皺眉頭，眼神裡充滿了困惑和挑戰。她知道，這並不是一項簡單的任務。但她沒有表現出一絲的畏難情緒，反而躍躍欲試。她深吸了一口氣，放鬆了自己的肩膀，然後開始嘗試著找出可能的路徑。

小悅首先使用了一個廣度優先搜尋（BFS）的策略。她從起點開始，每一步都嘗試所有可能的路徑，直到找到終點或者所有可能的路徑都被排除。在這個過程中，她需要儲存所有路徑的資訊，並且在探索過程中進行有效的回溯。

時間在不知不覺中流逝，小悅的臉上依然保持著淡定的神情。她的眼睛緊緊盯著迷宮圖，目光中閃爍著思考的光芒。雖然解題的過程充滿了挑戰，但是她依然保持著冷靜和專注。

當小悅遇到困難時，她並沒有表現出一絲的焦慮或者急躁。相反，她更加專注於自己的思考和分析。她反覆地觀察著迷宮的特點，嘗試著找到突破口。她的手指在鍵盤上輕輕地敲擊著，她在不斷地嘗試和修正自己的路徑演演算法。她的表情從認真到困惑，再到若有所思，最後到胸有成竹，這些微妙的變化都展示出她的解題過程是如此迷人。

經過一段時間的思考和探索，小悅終於找到了一個可行的路徑演演算法。她的臉上露出了欣喜的笑容，這是她在解題過程中最美的表情。她的眼睛閃爍著興奮的光芒，這是她在成功的喜悅中最為動人的地方。她輕輕地鬆開了握緊的拳頭，似乎在跟自己的勝利慶祝。最終，小悅成功地解出了這個迷宮，她的臉上露出了一絲得意的笑容。

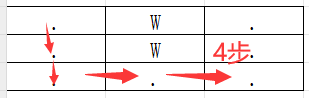
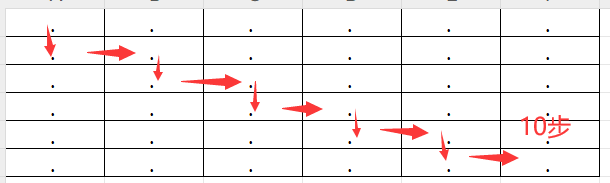
小悅面臨的迷宮最短路徑圖例如下，她需要繞開W表示的牆，然後通過計算得到從(0,0)到終點(2,2)或(5,5)或(n,n)的最短路徑步數：

3X3圖例：

6X6圖例：

演演算法實現1:

 1     public static int PathFinder(string maze)
 2     {
 3         // 將迷宮字串轉換為二維陣列
 4         string[] rows = maze.Split('\n');
 5         int n = rows.Length; char[,] grid = new char[n, n];
 6         for (int i = 0; i < n; i++)
 7         { for (int j = 0; j < n; j++) { grid[i, j] = rows[i][j]; } }
 8 
 9         // 建立一個佇列來執行廣度優先搜尋
10         Queue<(int, int)> queue = new Queue<(int, int)>();
11         queue.Enqueue((0, 0));
12 
13         // 建立一個二維陣列來儲存到達每個位置的最小步數
14         int[,] steps = new int[n, n];
15         for (int i = 0; i < n; i++)
16         {
17             for (int j = 0; j < n; j++)
18             {
19                 steps[i, j] = int.MaxValue;
20             }
21         }
22         steps[0, 0] = 0;
23 
24         // 定義四個基本方向
25         int[] dx = { 0, 0, 1, -1 };
26         int[] dy = { 1, -1, 0, 0 };
27 
28         // 執行廣度優先搜尋
29         while (queue.Count > 0)
30         {
31             var (x, y) = queue.Dequeue();
32 
33             // 檢查是否到達出口
34             if (x == n - 1 && y == n - 1)
35             {
36                 return steps[x, y];
37             }
38 
39             // 探索四個基本方向
40             for (int i = 0; i < 4; i++)
41             {
42                 int nx = x + dx[i];
43                 int ny = y + dy[i];
44 
45                 // 檢查新位置是否在迷宮邊界內
46                 if (nx >= 0 && nx < n && ny >= 0 && ny < n)
47                 {
48                     // 檢查新位置是否為空並且可以移動到該位置
49                     if (grid[nx, ny] == '.' && steps[x, y] + 1 < steps[nx, ny])
50                     {
51                         steps[nx, ny] = steps[x, y] + 1;
52                         queue.Enqueue((nx, ny));
53                     }
54                 }
55             }
56         }
57 
58         // 如果執行到這裡，表示沒有路徑到達出口
59         return -1;
60     }

這段程式碼實現了一個迷宮路徑搜尋的演演算法。它使用了c#的Queue物件和二維陣列來完成搜尋過程。

Queue物件：在這段程式碼中，Queue<(int, int)> queue = new Queue<(int, int)>(); 建立了一個佇列，用於執行廣度優先搜尋。佇列是一種先進先出（FIFO）的資料結構，它可以用來儲存一系列元素，並按照它們被新增的順序進行處理。在這個演演算法中，佇列用於儲存待探索的位置座標，以便按照廣度優先的順序進行搜尋。
二維陣列：int[,] steps = new int[n, n]; 建立了一個二維陣列，用於儲存到達每個位置的最小步數。二維陣列是一個由行和列組成的表格結構，可以用來表示和操作二維資料。在這個演演算法中，二維陣列用於記錄從起點到達每個位置的最小步數，以便在搜尋過程中更新和比較步數。

區別：

Queue物件是一個動態大小的資料結構，可以在執行時新增和刪除元素。它適用於需要按照先進先出的順序處理元素的場景，比如廣度優先搜尋、任務排程等。而IList物件是一個介面，它定義了一組用於存取和操作元素的方法和屬性。IList介面的實現類（如List）可以用來建立一個可變大小的集合，可以通過索引存取和修改元素。
二維陣列是一個固定大小的表格結構，它的行數和列數在建立時就確定，無法在執行時改變。二維陣列適用於需要表示和操作二維資料的場景，比如矩陣運算、影象處理等。而IList物件可以通過List、ArrayList等實現類來建立一個可變大小的集合，可以動態新增和刪除元素。

在這個演演算法中，使用Queue<(int,int)>物件是合適的，因為廣度優先搜尋需要按照先進先出的順序處理元素。Queue<(int,int)>物件提供了Enqueue()和Dequeue()方法，可以方便地實現先進先出的邏輯。

雖然IList<(int,int)>物件也可以用來實現廣度優先搜尋，但是需要手動實現佇列的先進先出的邏輯，比如使用Add()方法新增元素到末尾，使用RemoveAt(0)方法移除隊首元素。這樣會增加程式碼的複雜性，並且效能可能不如直接使用Queue<(int,int)>物件。

通過測試用例解釋演演算法：

 1     public void TestBasic()
 2     {
 3 
 4         string a = ".W.\n" +
 5                    ".W.\n" +
 6                    "...",
 7 
 8                b = ".W.\n" +
 9                    ".W.\n" +
10                    "W..",
11 
12         Assert.AreEqual(4, Finder.PathFinder(a));
13         Assert.AreEqual(-1, Finder.PathFinder(b));
14     }

首先，我們定義了兩個測試用例a和b。a和b都是由三行三列的字元矩陣表示的迷宮。其中，字元'.'表示可以通過的路徑，字元'W'表示牆。

對於測試用例a，迷宮矩陣如下：

.W.
.W.
...

我們希望找到從起點(0, 0)到終點(2, 2)的最短路徑。在迷宮中，我們可以向右移動兩步，然後向下移動兩步，即可到達終點。因此，最短路徑的步數為4。

對於測試用例b，迷宮矩陣如下：

.W.
.W.
W..

我們希望找到從起點(0, 0)到終點(2, 2)的最短路徑。在迷宮中，無論如何移動，都無法到達終點。因為迷宮中的第三行全部是牆，無法通過。因此，不存在從起點到終點的路徑，返回-1。

在PathFinder演演算法中，我們首先將迷宮字串轉換為二維陣列，並建立一個佇列來執行廣度優先搜尋。然後，我們建立一個二維陣列來儲存到達每個位置的最小步數。初始時，所有位置的最小步數都設定為最大值，除了起點位置的最小步數為0。

var (x, y) = queue.Dequeue();用於從佇列中取出隊首元素，並將其賦值給變數(x, y)。在這個演演算法中，(x, y)表示當前位置的座標。

queue.Enqueue((nx, ny));用於將新位置的座標(nx, ny)加入佇列中。在這個演演算法中，我們在探索四個基本方向時，如果新位置滿足條件，就將其加入佇列中，以便在下一輪迴圈中繼續探索該位置。通過使用佇列，我們可以確保廣度優先搜尋按照層級順序進行，從而找到最短路徑的步數。

接下來，我們使用一個while迴圈來執行廣度優先搜尋。在每一輪迴圈中，我們從佇列中取出隊首元素，並檢查是否到達出口。如果到達出口，則返回該位置的最小步數。否則，我們探索四個基本方向，並檢查新位置是否在迷宮邊界內，是否為空並且可以移動到該位置。如果滿足條件，我們更新新位置的最小步數，並將新位置加入佇列中。

最後，如果執行到迴圈結束仍然沒有找到路徑到達出口，則返回-1。

演演算法實現2(遞迴洪水填充)：

洪水遞迴填充演演算法，也稱為洪水填充演演算法或種子填充演演算法，是一種用於計算機圖學中的影象處理技術。它的目標是根據給定的種子點和閾值，將影象中的某個區域進行填充。

這個演演算法的由來可以追溯到計算機圖學的早期。在早期的計算機圖學中，人們希望能夠通過計算機來實現影象的自動填充，以便進行影象編輯和處理。而洪水遞迴填充演演算法就是為了滿足這個需求而提出的。

洪水遞迴填充演演算法的基本思想是從種子點開始，將其顏色值擴散到相鄰的畫素點，然後再遞迴地將這些畫素點的顏色值擴散到它們的相鄰畫素點，直到達到某個結束條件。這個結束條件通常是畫素點的顏色值與種子點的顏色值不同或者達到了設定的閾值。

洪水遞迴填充演演算法的優勢在於它的簡單性和效率。它只需要對每個畫素點進行一次顏色值的比較和填充操作，而不需要對整個影象進行復雜的計算。因此，它在處理簡單的影象填充任務時非常高效。

洪水遞迴填充演演算法在許多影象編輯和處理軟體中得到了廣泛應用。例如，它可以用於影象的背景去除、影象的顏色替換、影象的區域分割等任務。它也可以用於計算機遊戲中的地圖填充、連連看遊戲中的消除演演算法等場景。

 1 using System.Linq;
 2 using static System.Math;
 3 
 4 public class Finder
 5 {
 6     public static int PathFinder(string maze)
 7     {
 8         // 將迷宮字串轉換為二維陣列
 9         var m = maze.Split('\n').Select(a => a.Select(b => (b == '.') ? 999 : 0).ToArray()).ToArray(); 
10         // 從起點開始執行遞迴洪水填充
11         Flood(0, 0, m, 0);
12         // 返回終點的最小步數，如果沒有路徑到達終點，則返回-1
13         return m.Last().Last() < 999 ? m.Last().Last() : -1;
14     }
15 
16     
17     private static void Flood(int x, int y, int[][] m, int step)
18     { 
19         // 檢查當前位置是否可以到達
20         if (Min(x, y) > -1 && Max(x, y) < m.GetLength(0) && m[x][y] > step)
21         { // 更新當前位置的最小步數
22             m[x][y] = step; // 探索四個基本方向
23             var d = new[] { 0, 0, 1, -1 };
24             for (int i = 0; i < 4; i++) Flood(x + d[i], y + d[3 - i], m, step + 1);
25         }
26     }
27 }

對比演演算法1和演演算法2，可以得出以下結論：

效率和效能：演演算法1使用佇列來執行廣度優先搜尋，而演演算法2使用遞迴洪水填充演演算法來執行搜尋。在某些情況下，遞迴函數可能比佇列更高效。遞迴函數可以避免佇列入隊出隊的操作，節省了一些時間和空間開銷。因此，演演算法2可能比演演算法1更高效。
如果迷宮規模較小且不太複雜，可以選擇演演算法1。演演算法1使用佇列和二維陣列來進行搜尋，程式碼更直觀易懂。如果迷宮規模較大或者複雜度較高，建議選擇演演算法2。演演算法2使用遞迴函數和一維陣列來進行搜尋，可能更高效。另外，演演算法2還可以節省一些記憶體空間。

這兩個演演算法可以應用於汽車導航躲避擁堵和路線計算等場景。

演演算法1（廣度優先搜尋）：廣度優先搜尋演演算法可以用於計算最短路徑。在汽車導航中，可以使用廣度優先搜尋來計算最短路徑以避免擁堵。通過將道路網格化，每個網格表示一個道路交叉口或路段，可以使用廣度優先搜尋演演算法來找到從起點到終點的最短路徑。通過計算每個網格的最小步數，可以確定最短路徑，並根據步數來規劃導航路線。
演演算法2（遞迴洪水填充）：遞迴洪水填充演演算法可以用於計算到達目標位置的最小步數。在汽車導航中，可以使用遞迴洪水填充演演算法來計算到達目標位置的最小時間或最小距離。通過將道路網格化，每個網格表示一個道路交叉口或路段，可以使用遞迴洪水填充演演算法來計算從起點到每個網格的最小步數。通過計算每個網格的最小步數，可以確定最短路徑，並根據步數來規劃導航路線。

除了汽車導航，這兩個演演算法還可以應用於以下場景：

遊戲開發：廣度優先搜尋演演算法可以用於遊戲中的路徑規劃，例如尋找最短路徑或避免障礙物。遞迴洪水填充演演算法可以用於遊戲中的區域填充，例如地圖生成或區域探索。
影象處理：廣度優先搜尋演演算法可以用於影象分割，例如將影象分割為不同的區域或物件。遞迴洪水填充演演算法可以用於影象填充，例如顏色填充或影象修復。
社群網路分析：廣度優先搜尋演演算法可以用於社群網路中的關係分析，例如尋找兩個人之間的最短路徑或查詢具有特定關係的人。遞迴洪水填充演演算法可以用於社群網路中的資訊傳播分析，例如查詢資訊傳播的路徑或影響力傳播的範圍。
網路路由：廣度優先搜尋演演算法可以用於網路路由中的路由選擇，例如尋找最短路徑或避免擁堵。遞迴洪水填充演演算法可以用於網路路由中的路由優化，例如根據網路拓撲和流量情況來優化路由選擇。

雖然這兩個演演算法的實現方式和應用場景不同，但它們都可以用於解決路徑規劃和區域填充等問題。在實際應用中，可以根據具體的需求和場景選擇合適的演演算法。

可以將演演算法1修改為同時返回最小步數和路徑的形式：

修改之後的PathFinder演演算法已具有一定的實用價值，可以實現找到避免擁堵的最短路徑，並實時顯示在地圖上。

 1 public static (int, List<(int, int)>) PathFinder(string maze)
 2 {
 3     // 將迷宮字串轉換為二維陣列
 4     string[] rows = maze.Split('\n');
 5     int n = rows.Length;
 6     char[,] grid = new char[n, n];
 7     for (int i = 0; i < n; i++)
 8     {
 9         for (int j = 0; j < n; j++)
10         {
11             grid[i, j] = rows[i][j];
12         }
13     }
14     
15     // 建立一個佇列用於執行廣度優先搜尋
16     Queue<(int, int)> queue = new Queue<(int, int)>();
17     queue.Enqueue((0, 0));
18     
19     // 建立一個二維陣列來儲存到達每個位置的最小步數
20     int[,] steps = new int[n, n];
21     for (int i = 0; i < n; i++)
22     {
23         for (int j = 0; j < n; j++)
24         {
25             steps[i, j] = int.MaxValue;
26         }
27     }
28     steps[0, 0] = 0;
29     
30     // 建立一個二維陣列來儲存每個位置的前一個位置
31     (int, int)[,] prev = new (int, int)[n, n];
32     
33     // 定義四個方向：上、下、左、右
34     int[] dx = { 0, 0, 1, -1 };
35     int[] dy = { 1, -1, 0, 0 };
36     
37     // 執行廣度優先搜尋
38     while (queue.Count > 0)
39     {
40         var (x, y) = queue.Dequeue();
41         
42         // 檢查是否抵達出口
43         if (x == n - 1 && y == n - 1)
44         {
45             // 使用前一個位置的資訊構建路徑
46             List<(int, int)> path = new List<(int, int)>();
47             path.Add((x, y));
48             while (x != 0 || y != 0)
49             {
50                 var (px, py) = prev[x, y];
51                 path.Add((px, py));
52                 x = px;
53                 y = py;
54             }
55             path.Reverse();
56             
57             return (steps[x, y], path);
58         }
59         
60         // 探索四個方向
61         for (int i = 0; i < 4; i++)
62         {
63             int nx = x + dx[i];
64             int ny = y + dy[i];
65             
66             // 檢查新位置是否在迷宮邊界內
67             if (nx >= 0 && nx < n && ny >= 0 && ny < n)
68             {
69                 // 檢查新位置是否為空並且可以移動到它
70                 if (grid[nx, ny] == '.' && steps[x, y] + 1 < steps[nx, ny])
71                 {
72                     steps[nx, ny] = steps[x, y] + 1;
73                     prev[nx, ny] = (x, y);
74                     queue.Enqueue((nx, ny));
75                 }
76             }
77         }
78     }
79     
80     // 如果到達這裡，表示沒有路徑到達出口
81     return (-1, null);
82 }

測試用例：

  1 using NUnit.Framework;
  2 using System;
  3 using System.Collections.Generic;
  4 using System.Linq;
  5 using System.Text;
  6 
  7 public class SolutionTest
  8 {
  9 
 10     [Test]
 11     public void TestBasic()
 12     {
 13 
 14         string a = ".W.\n" +
 15                    ".W.\n" +
 16                    "...",
 17 
 18                b = ".W.\n" +
 19                    ".W.\n" +
 20                    "W..",
 21 
 22                c = "......\n" +
 23                    "......\n" +
 24                    "......\n" +
 25                    "......\n" +
 26                    "......\n" +
 27                    "......",
 28 
 29                d = "......\n" +
 30                    "......\n" +
 31                    "......\n" +
 32                    "......\n" +
 33                    ".....W\n" +
 34                    "....W.";
 35 
 36         Assert.AreEqual(4, Finder.PathFinder(a));
 37         Assert.AreEqual(-1, Finder.PathFinder(b));
 38         Assert.AreEqual(10, Finder.PathFinder(c));
 39         Assert.AreEqual(-1, Finder.PathFinder(d));
 40     }
 41 
 42     [Test]
 43     public void TestRandom50()
 44     {
 45 
 46         for (int i = 0; i < 50; i++)
 47         {
 48             int len = 4 + rand.Next(7);
 49             string str = RandomMaze(len);
 50             Console.WriteLine(str+ '\n');
 51             Assert.AreEqual(TestFinder.PathFinder(str), Finder.PathFinder(str), str);
 52         }
 53     }
 54 
 55     [Test]
 56     public void TestRandomBigMaze10()
 57     {
 58         for (int i = 0; i < 10; i++)
 59         {
 60             String str = RandomMaze(100);
 61             Assert.AreEqual(TestFinder.PathFinder(str), Finder.PathFinder(str), str);
 62         }
 63     }
 64 
 65     [Test]
 66     public void TestSnakesLabirinth()
 67     {
 68 
 69         Assert.AreEqual(96, Finder.PathFinder(
 70         ".W...W...W...\n" +
 71         ".W.W.W.W.W.W.\n" +
 72         ".W.W.W.W.W.W.\n" +
 73         ".W.W.W.W.W.W.\n" +
 74         ".W.W.W.W.W.W.\n" +
 75         ".W.W.W.W.W.W.\n" +
 76         ".W.W.W.W.W.W.\n" +
 77         ".W.W.W.W.W.W.\n" +
 78         ".W.W.W.W.W.W.\n" +
 79         ".W.W.W.W.W.W.\n" +
 80         ".W.W.W.W.W.W.\n" +
 81         ".W.W.W.W.W.W.\n" +
 82         "...W...W...W."));
 83 
 84     }
 85 
 86     [Test]
 87     public void TestVerySmallLabirinth()
 88     {
 89 
 90         Assert.AreEqual(0, Finder.PathFinder("."));
 91     }
 92 
 93     private static readonly Random rand = new Random();
 94     private string RandomMaze(int len)
 95     {
 96 
 97         string template = new string('.', len);
 98         StringBuilder[] maze = Enumerable.Range(0, len).Select(i => new StringBuilder(template)).ToArray();
 99 
100         for (int j = 0; j < len * len / 3; j++)
101         {
102             maze[rand.Next(len)][rand.Next(len)] = 'W';
103         }
104         maze[0][0] = '.';
105         maze[len - 1][len - 1] = '.';
106         return string.Join("\n", maze.Select(b => b.ToString()));
107     }
108 
109     private class TestFinder
110     {
111         public static int PathFinder(string maze)
112         {
113             return new TestFinder().find(maze);
114         }
115 
116         private string[] m;
117         private int[,] steps;
118         private Queue<int[]> front;
119         private int goal;
120 
121         public int find(string maze)
122         {
123             m = maze.Split('\n');
124 
125             steps = new int[m.Length, m.Length];
126 
127             steps[0, 0] = 1;
128             front = new Queue<int[]>();
129             front.Enqueue(new[] { 0, 0 });
130 
131             goal = m.Length - 1;
132 
133             while (front.Any())
134             {
135 
136                 int[] c = front.Dequeue();
137 
138                 if (c[0] == goal && c[1] == goal)
139                     return steps[goal, goal] - 1;
140 
141                 int step = steps[c[0], c[1]] + 1;
142                 TryStep(c[0] - 1, c[1], step);
143                 TryStep(c[0] + 1, c[1], step);
144                 TryStep(c[0], c[1] - 1, step);
145                 TryStep(c[0], c[1] + 1, step);
146 
147             }
148             return -1;
149         }
150 
151         private void TryStep(int r, int c, int v)
152         {
153             if (r < 0 || r > goal || c < 0 || c > goal || steps[r, c] != 0)
154                 return;
155 
156             string row = m[r];
157             if (row[c] == '.')
158             {
159                 steps[r, c] = v;
160                 front.Enqueue(new int[] { r, c });
161             }
162         }
163     }
164 }