1.問題場景

有100億個url被加入了黑名單，現在提供一個url要去判斷是否屬於黑名單。也就是一個很簡單的一個東西是否屬於一個集合的問題。

一般來說用set就能解決這種問題，但是由於url數目太多，記憶體中無法開闢一個這麼大的空間去存放所有url，這個時候就需要我們去使用一種結構，去減少狀態資訊儲存所需要的記憶體，而布隆過濾器就可以很好地實現這個功能。

2.基本知識

在瞭解布隆過濾器演演算法前，需要先了解一些前置知識，例如雜湊函數和點陣圖

雜湊函數

雜湊函數就是一個對映函數，可以把任意長的輸入位（或位元組）變化成固定長的輸出字串的一種函數。理想的雜湊函數是從所有可能的輸入值得到所可能的有限輸出值的一個隨機對映。

性質

雜湊函數保證有離散性，即當m1和m2 這兩個輸入有一點差別的時候，最終經過雜湊函數計算的輸出結果可能完全不同，離散開來。
對於相同的輸入，雜湊函數計算的輸出一定會相同，反過來只要輸出不相同，那麼輸入一定就不會相同。對於不同的輸入，極小概率下，雜湊函數的計算輸出會相同（即雜湊碰撞），一般都不同。
同時雜湊函數也保證有均勻性，即在輸出的大範圍裡，每一小片區域中存在的值的個數是相近的（舉例：一共有1000個值被輸出，在整個輸出範圍裡，每一小片區域裡包含的值的個數基本相同）。
hash函數為單向函數，給定訊息m可以很容易計算h(m)，但對於給定的x，不能求出滿足x=h(m)的m

總而言之，雜湊函數就是一個對映函數，計算的結果H（m）會在值域上離散均勻分佈

點陣圖

點陣圖，bitmap或者bitarray，就是用bit位去儲存資訊的一種結構。正常的陣列要麼是int陣列或者是long陣列，每個元素是4位元組或者8位元組，也就是32bit或者64bit的資訊表示一個元素或者一種狀態。而bitarray就是1個bit表示陣列裡的一個元素或者一種狀態，這樣的優點就是非常省空間，本來用幾十個bit表達的資訊被它用1個bit就表達了（前提是資訊能用點陣圖表達的情況下）。

下面一串數位0和1即是點陣圖的表示，一共有32個數位，分別表示陣列裡的32個元素，這些元素的值要麼是0要麼是1。

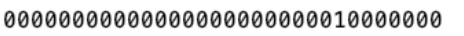
因為點陣圖的每一個元素只有2個值，一般可以用來判斷一個數是否出現過這種簡單的布林值是或否的問題。

如何實現一個點陣圖？因為我們的數位都是32或64bit的，所以需要藉助真實的數位來實現bitmap。現在設一個數位是32個bit，現在有一個長度位10的陣列，這個陣列可以用來表示長度為320的bit型別的陣列，然後通過位運算去實現從bit陣列裡面取值

    const arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    let i = 199 //想要獲取bit陣列裡第199個元素的值
    let numIndex = Math.floor(i / 32) //找到arr裡的對應的元素
    let bitIndex = i % 32 //找到對應元素裡的位數
    let value = (arr[numIndex] >> bitIndex) & 1 //獲取第199位的值

對bitarray進行賦值操作

    arr[numIndex] = arr[numIndex] | (1 << bitIndex) //將第199位變成1
    arr[numIndex] = arr[numIndex] & (~(1 << bitIndex)) //將199位變成0

實現BitMap類

程式碼、案例如下

    class BitMap {
        constructor(size) {
            this.size = Math.ceil(size / 32)
            this.bitArray = new Array(this.size).fill(0)
        }
        getNumber(num) {
            //獲取位數
            let numIndex = Math.floor(num / 32)
            let bitIndex = num % 32
            return (this.bitArray[numIndex] >> bitIndex) & 1
        }
        isExist(num) {
            //判斷一個數是否存在
            let value = this.getNumber(num)
            return value == 1
        }
        addNumber(num) {
            //新增一個數
            let numIndex = Math.floor(num / 32)
            let bitIndex = num % 32
            this.bitArray[numIndex] = this.bitArray[numIndex] | (1 << bitIndex)
        }
    }

舉例，現在有一個arr陣列，arr陣列裡每個元素都是0-100的數，給定一個值x判斷x是否出現過。

建立一個BitMap陣列，這個bit陣列只要4個元素（4個元素就可表示128位元的資訊）。
遍歷arr陣列，呼叫addNumber方法，出現過一個數就把bit陣列的對應索引位置設定為1
呼叫isExist方法判斷bit陣列的索引x是否為1是1就說明出現過，否則就沒出現過

對於這種值範圍是給定的情況下，相比起普通的建立map或set統計是否出現過，這個做法只需要4個元素的額外陣列空間，大大節省了空間

3.布隆過濾器

回到前面的問題，對於100億個url的黑名單，現在希望也可以通過點陣圖的方式來完成判斷一個url是否出現在黑名單內，這樣可以極大地壓縮空間，但是url這種字串是無法直接使用點陣圖的，所以需要藉助雜湊函數的對映。

雜湊函數的值域可以是一個數位，所以把url作為雜湊函數的輸入，就可以得到一個數位，即H(url) = number
點陣圖需要把範圍規定在0-m的一個範圍，所以可以對雜湊函數的計算結果number模上一個m，就可以把所有url經過雜湊函數後的計算結果限制在0-m內了

此時已經把url變成0-m的數位了，已經可以直接用點陣圖去判斷是否存在了，但是仍然有一個問題，就是雜湊碰撞。不同的輸入也有可能會有相同的輸出，如果m不夠大，很可能存在一個不在黑名單的url在經過雜湊函數的計算和取模之後，結果與黑名單中url的計算結果相同，那麼不在黑名單的url就會被誤判誤封。

解決這個問題的辦法可以是

取足夠大的m，但是m仍然會受到記憶體大小的限制
選k個雜湊函數，對每一個url都用這k個雜湊函數計算，然後分別模上m，然後把這些結果全部新增到點陣圖裡（把對應索引處的元素值改成1）。當然對於想要判斷的那個url，也要用這個k個雜湊函數分別計算取模，然後拿這k個結果作為索引去點陣圖裡取值，只有當發現點陣圖裡這k個索引裡的值全是1的時候，才判定url是黑名單url，只要存在一個位置是0，就說明不是黑名單url，因為如果是黑名單url，所有k個索引處的值一定都已經做過新增，都是1。通過k個雜湊函數的計算，相比起僅用1個雜湊函數計算失誤率就降低了不少。

而m和k的取值則要取決於樣本量n和允許的失誤率p

m自然是樣本越多，允許的失誤率越低，取得值越大，當然記憶體足夠的情況下也可以取得比公式裡更多，這樣可以降低失誤率

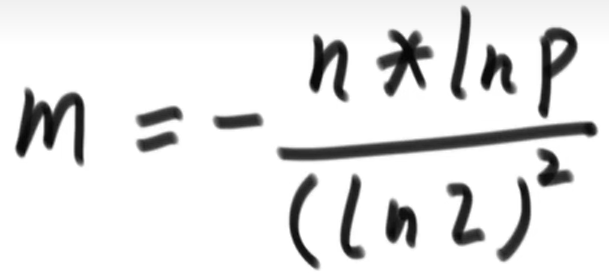
k的取值取決於m和n的比例，如果k取得太少，那麼和之前的1個雜湊函數計算差別不大，如果k取得太大，一次計算下來很多位置都設定成了1，再想判斷的時候就很可能失誤

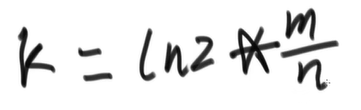
設定好了m和k，就可以按照之前的點陣圖演演算法來進行判斷一個url是否是黑名單內的url了

大集合裡查詢資料-布隆過濾器

1.問題場景

2.基本知識

雜湊函數

點陣圖

3.布隆過濾器