Java演演算法之動態規劃詳解-買賣股票最佳時機

①動態規劃

動態規劃（Dynamic Programming，DP）是運籌學的一個分支，是求解決策過程最佳化的過程。20世紀50年代初，美國數學家貝爾曼（R.Bellman）等人在研究多階段決策過程的優化問題時，提出了著名的最優化原理，從而創立了動態規劃。動態規劃的應用極其廣泛，包括工程技術、經濟、工業生產、軍事以及自動化控制等領域，並在揹包問題、生產經營問題、資金管理問題、資源分配問題、最短路徑問題和複雜系統可靠性問題等中取得了顯著的效果

⓿動規五部曲

1. 確定dp陣列以及下標的含義
2. 確定遞推公式
3. dp陣列如何初始化
4. 確定遍歷順序
5. 舉例推導dp陣列

❶基礎規劃題

509. 斐波那契數

斐波那契數 （通常用 F(n) 表示）形成的序列稱為 斐波那契數列 。該數列由 0 和 1 開始，後面的每一項數位都是前面兩項數位的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

給定 n ，請計算 F(n) 。

範例 1：

輸入：n = 2
輸出：1
解釋：F(2) = F(1) + F(0) = 1 + 0 = 1

範例 2：

輸入：n = 3
輸出：2
解釋：F(3) = F(2) + F(1) = 1 + 1 = 2

範例 3：

輸入：n = 4
輸出：3
解釋：F(4) = F(3) + F(2) = 2 + 1 = 3

//動態規劃
class Solution {
    public int fib(int n) {
        if (n < 2) return n;
        int dp[] = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}
//優化
class Solution {
    public int fib(int n) {
        if (n < 2) return n;
        int a = 0, b = 1, c = 0;
        for (int i = 2; i <= n; i++) {
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }
}

//遞迴
class Solution {
    public int fib(int n) {
        if (n < 2) return n;
        return fib(n - 1) + fib(n - 2);
    }
}

70. 爬樓梯

假設你正在爬樓梯。需要 n 階你才能到達樓頂。

每次你可以爬 1 或 2 個臺階。你有多少種不同的方法可以爬到樓頂呢？

範例 1：

輸入：n = 2
輸出：2
解釋：有兩種方法可以爬到樓頂。
1. 1 階 + 1 階
2. 2 階

範例 2：

輸入：n = 3
輸出：3
解釋：有三種方法可以爬到樓頂。
1. 1 階 + 1 階 + 1 階
2. 1 階 + 2 階
3. 2 階 + 1 階

---

本問題其實常規解法可以分成多個子問題，爬第n階樓梯的方法數量，等於 2 部分之和

1. 爬上 n−1 階樓梯的方法數量。因為再爬1階就能到第n階
2. 爬上 n−2 階樓梯的方法數量，因為再爬2階就能到第n階

所以我們得到公式 dp[n] = dp[n−1] + dp[n−2]，同時需要初始化 dp[0]=1 和 dp[1]=1

時間複雜度：O(n)

class Solution {
    public int climbStairs(int n) {
        int dp[] = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

746. 使用最小花費爬樓梯

給你一個整數陣列 cost ，其中 cost[i] 是從樓梯第 i 個臺階向上爬需要支付的費用。一旦你支付此費用，即可選擇向上爬一個或者兩個臺階。

你可以選擇從下標為 0 或下標為 1 的臺階開始爬樓梯。

請你計算並返回達到樓梯頂部的最低花費。

範例 1：

輸入：cost = [10,15,20]
輸出：15
解釋：你將從下標為 1 的臺階開始。
- 支付 15 ，向上爬兩個臺階，到達樓梯頂部。
總花費為 15 。

範例 2：

輸入：cost = [1,100,1,1,1,100,1,1,100,1]
輸出：6
解釋：你將從下標為 0 的臺階開始。
- 支付 1 ，向上爬兩個臺階，到達下標為 2 的臺階。
- 支付 1 ，向上爬兩個臺階，到達下標為 4 的臺階。
- 支付 1 ，向上爬兩個臺階，到達下標為 6 的臺階。
- 支付 1 ，向上爬一個臺階，到達下標為 7 的臺階。
- 支付 1 ，向上爬兩個臺階，到達下標為 9 的臺階。
- 支付 1 ，向上爬一個臺階，到達樓梯頂部。
總花費為 6 。

---

1. 確定dp陣列以及下標的含義

• dp[i]的定義：到達第i臺階所花費的最少體力為dp[i]

1. 確定遞推公式

• 有兩個途徑得到dp[i]，一個是dp[i-1] 一個是dp[i-2]
  • dp[i - 1] 跳到 dp[i] 需要花費 dp[i - 1] + cost[i - 1]。
  • dp[i - 2] 跳到 dp[i] 需要花費 dp[i - 2] + cost[i - 2]。
• 那麼究竟是選從dp[i - 1]跳還是從dp[i - 2]跳呢？
• 一定是選最小的，所以 dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

1. dp陣列如何初始化

題目描述中明確說了 「你可以選擇從下標為 0 或下標為 1 的臺階開始爬樓梯。」 也就是說到達第 0 、1個臺階是不花費的，但從 第0 個臺階往上跳的話，需要花費 cost[0]。所以初始化 dp[0] = 0，dp[1] = 0;

1. 確定遍歷順序

因為是模擬臺階，而且dp[i]由dp[i-1]dp[i-2]推出，所以是從前到後遍歷cost陣列就可以了。

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int dp[] = new int[n + 1];
        dp[0] = 0;
        dp[1] = 0;
        for(int i = 2; i <= n; i++){
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
       return dp[n];
    }
}

118. 楊輝三角

給定一個非負整數 numRows，生成「楊輝三角」的前 numRows 行。

在「楊輝三角」中，每個數是它左上方和右上方的數的和。

範例 1:

輸入: numRows = 5
輸出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

範例 2:

輸入: numRows = 1
輸出: [[1]]

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> res = new ArrayList<>();
        for(int i = 0; i < numRows; i++){
            List<Integer> row = new ArrayList<Integer>();
            for (int j = 0; j <= i; j++) {
                if(j == 0 || j == i) row.add(1);
                else row.add(res.get(i - 1).get(j - 1) + res.get(i - 1).get(j));
            }
            res.add(row);
        }
        return res;
    }
}

62. 不同路徑

一個機器人位於一個 m x n 網格的左上角 （起始點在下圖中標記為 「Start」 ）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為 「Finish」 ）。

問總共有多少條不同的路徑？

範例 1：

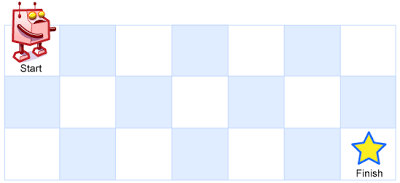
輸入：m = 3, n = 7
輸出：28

範例 2：

輸入：m = 3, n = 2
輸出：3
解釋：
從左上角開始，總共有 3 條路徑可以到達右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

範例 3：

輸入：m = 7, n = 3
輸出：28

範例 4：

輸入：m = 3, n = 3
輸出：6

---

我們令 dp[i][j] 是到達 i, j 最多路徑

動態方程：dp[i][j] = dp[i-1][j] + dp[i][j-1]

注意，對於第一行 dp[0][j]，或者第一列 dp[i][0]，由於都是在邊界，所以只能為 1

class Solution {
    public int uniquePaths(int m, int n) {
        int dp[][] = new int[m][n];
        //初始化
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                //到達i行j列的路徑條數
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

63. 不同路徑 II

一個機器人位於一個 m x n 網格的左上角 （起始點在下圖中標記為 「Start」 ）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為 「Finish」）。

現在考慮網格中有障礙物。那麼從左上角到右下角將會有多少條不同的路徑？

網格中的障礙物和空位置分別用 1 和 0 來表示。

範例 1：

輸入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
輸出：2
解釋：3x3 網格的正中間有一個障礙物。
從左上角到右下角一共有 2 條不同的路徑：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

範例 2：

輸入：obstacleGrid = [[0,1],[0,0]]
輸出：1

---

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int dp[][] = new int[m][n];
        for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++){
            dp[i][0] = 1;
        }
        for(int j = 0; j < n && obstacleGrid[0][j] == 0; j++){
            dp[0][j] = 1;
        }
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                if(obstacleGrid[i][j] == 0){
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[m - 1][n - 1];
    }
}

343. 整數拆分

劍指 Offer 14- I. 剪繩子 - 力扣（Leetcode）

給定一個正整數 n ，將其拆分為 k 個 正整數 的和（ k >= 2 ），並使這些整數的乘積最大化。

返回 你可以獲得的最大乘積 。

範例 1:

輸入: n = 2
輸出: 1
解釋: 2 = 1 + 1, 1 × 1 = 1。

範例 2:

輸入: n = 10
輸出: 36
解釋: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

---

動規五部曲，分析如下：

1. 確定dp陣列以及下標的含義

dp[i]：分拆數位 i，可以得到的最大乘積為dp[i]。

1. 確定遞推公式

當 i ≥ 2 時，假設對正整數 i 拆分出的第一個正整數是 j（1 ≤ j < i），則有以下兩種方案：

• 將 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多個正整數，此時的乘積是 j×(i−j)；
• 將 i 拆分成 j 和 i−j 的和，且 i−j 繼續拆分成多個正整數，此時的乘積是 j×dp[i−j]。

遞推公式：dp[i]=max{dp[i], j×(i−j), j×dp[i−j]}

1. dp的初始化

初始化 dp[2] = 1

1. 確定遍歷順序

• 2 < i <= n
• 1 < j < i

for (int i = 3; i <= n ; i++) {
    for (int j = 1; j < i - 1; j++) {
        dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
    }
}

1. 舉例推導dp陣列

。。。

class Solution {
    public int integerBreak(int n) {
        int dp[] = new int[n + 1];
        dp[2] = 1;
        for(int i = 3; i <= n; i++){
            for(int j = 1; j < i; j++){
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        } 
        return dp[n];
    }
}

劍指 Offer 14- II. 剪繩子 II

給你一根長度為 n 的繩子，請把繩子剪成整數長度的 m 段（m、n都是整數，n>1並且m>1），每段繩子的長度記為 k[0],k[1]...k[m - 1] 。請問 k[0]*k[1]*...*k[m - 1] 可能的最大乘積是多少？例如，當繩子的長度是8時，我們把它剪成長度分別為2、3、3的三段，此時得到的最大乘積是18。

答案需要取模 1e9+7（1000000007），如計算初始結果為：1000000008，請返回 1。

範例 1：

輸入: 2
輸出: 1
解釋: 2 = 1 + 1, 1 × 1 = 1

範例 2:

輸入: 10
輸出: 36
解釋: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

每段長度取3最好

class Solution {
    public int cuttingRope(int n) {
        if(n == 2)
            return 1;
        if(n == 3)
            return 2;
        long res = 1;
        while(n > 4){
            //每一段取3進行累積
            res *= 3;
            res = res % 1000000007;
            n -= 3;
        }
        return (int)(res * n % 1000000007);//最後一段不能被3整除，累積上再取mod
    }
}

96. 不同的二元搜尋樹

給你一個整數 n ，求恰由 n 個節點組成且節點值從 1 到 n 互不相同的 二元搜尋樹 有多少種？返回滿足題意的二元搜尋樹的種數。

範例 1：

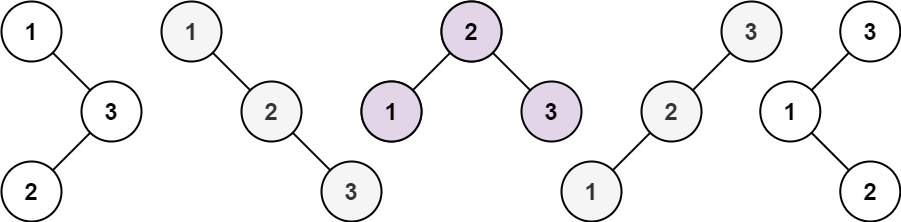
輸入：n = 3
輸出：5

範例 2：

輸入：n = 1
輸出：1

---

1. 確定dp陣列（dp table）以及下標的含義

dp[i] ： 1到i為節點組成的二元搜尋樹的個數為dp[i]。

1. 確定遞推公式

假設一共i個節點，對於根節點為j時，左子樹的節點個數為j-1，右子樹的節點個數為i-j

對於根節點為j時，其遞推關係， dp[i] = ∑(1<=j<=i) dp[左子樹節點數量] * dp[右子樹節點數量]，j是頭結點的元素，從1遍歷到i為止。

所以遞推公式：dp[i] += dp[j - 1] * dp[i - j];

1. dp陣列如何初始化

• dp[0] = 1;
• dp[1] = 1;

1. 確定遍歷順序

for (int i = 2; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
        
    }
}

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            for(int j = 1; j <= i; j++){
                dp[i] += dp[j - 1] * dp[i - j];   
            }
        }
        return dp[n];
    }
}

338. 位元位計數

給你一個整數 n ，對於 0 <= i <= n 中的每個 i ，計算其二進位制表示中 1 的個數 ，返回一個長度為 n + 1 的陣列 ans 作為答案。

範例 1：

輸入：n = 2
輸出：[0,1,1]
解釋：
0 --> 0
1 --> 1
2 --> 10

範例 2：

輸入：n = 5
輸出：[0,1,1,2,1,2]
解釋：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

進階：

• 很容易就能實現時間複雜度為 O(nlogn) 的解決方案，你可以線上性時間複雜度 O(n) 內用一趟掃描解決此問題嗎？
• 你能不使用任何內建函數解決此問題嗎？（如，C++ 中的 __builtin_popcount ）

---

動態規劃法

1. 如果這個數是偶數，那麼其二進位制中1的個數一定和其1/2的數二進位制中1的個數一樣，因為1/2就相當於右移1位，即把偶數的最後一個0去掉，不會影響1的個數。
   • res[i] = res[i / 2]
2. 如果這個數是奇數：那麼其二進位制中1的個數一定是其上一個偶數二進位制1的個數+1，因為就相當於將上一個偶數二進位制的最後1位的0變成1。
   • res[i] = res[i - 1] + 1—>res[i] = res[i / 2] + 1
3. 上述兩種情況可以合併成：res[i]的值等於 res[i/2]的值加上 i % 2 。
   • res[i / 2] + (i % 2)—>res[i >> 1] + (i & 1)

class Solution {
    public int[] countBits(int n) {
        int[] res = new int[n+1];
        res[0] = 0;
        for (int i = 1; i <= n; i++) {
            if (i % 2 == 1) {
                // 奇數：當前奇數的1的個數一定比上一個偶數+1
                res[i] = res[i - 1] + 1;
            } else {
                // 偶數：偶數1的個數一定和其1/2的偶數1的個數一樣
                res[i] = res[i / 2];
            }
        }
        return res;
    }
}

//優化
class Solution {
    public int[] countBits(int n) {
        int[] res = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            res[i] = res[i >> 1] + (i & 1);
        }
        return res;
    }
}

1137. 第 N 個泰波那契數

泰波那契序列 Tn 定義如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的條件下 Tn+3 = Tn + Tn+1 + Tn+2

給你整數 n，請返回第 n 個泰波那契數 Tn 的值。

範例 1：

輸入：n = 4
輸出：4
解釋：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

範例 2：

輸入：n = 25
輸出：1389537 

---

class Solution {
    int[] dp = new int[38]; //用於防止重複計算
    public int tribonacci(int n) {
        if(n == 0) return 0;
        if(n <= 2) return 1;
        int a = 0, b = 1, c = 1;
        for(int i = 3; i <= n; i++){
            int d = a + b + c;
            a = b;
            b = c;
            c = d;
        }
        return c;
    }
}

❷01揹包問題