演演算法解析:LeetCode——機器人碰撞和最低票價
摘要:本文由葡萄城技術團隊原創。轉載請註明出處:葡萄城官網,葡萄城為開發者提供專業的開發工具、解決方案和服務,賦能開發者。
機器人碰撞
問題:
現有 n 個機器人,編號從 1 開始,每個機器人包含在路線上的位置、健康度和移動方向。 給你下標從 0 開始的兩個整數陣列 positions、healths 和一個字串 directions(directions[i] 為 'L' 表示 向左 或 'R' 表示 向右)。positions 中的所有整數 互不相同 。 所有機器人以相同速度同時沿給定方向在路線上移動。如果兩個機器人移動到相同位置,則會發生 碰撞 。 如果兩個機器人發生碰撞,則將 健康度較低 的機器人從路線中 移除 ,並且另一個機器人的健康度 減少 1 。 倖存下來的機器人將會繼續沿著與之前 相同 的方向前進。如果兩個機器人的健康度相同,則將二者都從路線中移除。 請你確定全部碰撞後倖存下的所有機器人的 健康度 ,並按照原來機器人編號的順序排列。 即機器人 1 (如果倖存)的最終健康度,機器人 2 (如果倖存)的最終健康度等。 如果不存在倖存的機器人,則返回空陣列。 在不再發生任何碰撞後,請你以陣列形式,返回所有剩餘機器人的健康度(按機器人輸入中的編號順序)。
範例 :
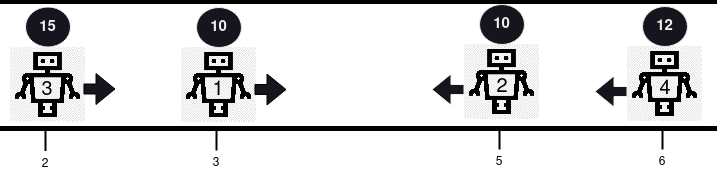
輸入:positions = [3,5,2,6], healths = [10,10,15,12], directions = "RLRL" 輸出:[14] 解釋:本例中發生 2 次碰撞。首先,機器人 1 和機器人 2 將會碰撞,因為二者健康度相同,二者都將被從路線中移除。接下來,機器人 3 和機器人 4 將會發生碰撞,由於機器人 4 的健康度更小,則它會被移除,而機器人 3 的健康度變為 15 - 1 = 14 。僅剩機器人 3 ,所以返回 [14] 。
提示: 1 <= positions.length == healths.length == directions.length == n <= 105 1 <= positions[i], healths[i] <= 109 directions[i] == 'L' 或 directions[i] == 'R' positions 中的所有值互不相同。
解決思路
用一個棧存放當前存活的機器人,按位元置從左至右(排序後的下標)遍歷機器人並判斷當前機器人的方向:
1. 如果當前機器人方向是 R,當前機器人推入棧,繼續處理下一個機器人;
2.如果方向是 L:
(1)如果棧為空,當前機器人推入棧,繼續處理下一個機器人;
(2) 如果棧頂元素方向也是 L,當前機器人推入棧,繼續處理下一個機器人;
(3) 比較與棧頂元素的健康度,判斷存活哪個:
- 如果棧頂存活,棧頂機器人健康度減 1,繼續處理下一個機器人;
- 如果當前存活,棧頂彈出,當前機器人健康度減 1,回到 2.3 ;
- 如果兩個都消失,棧頂彈出,繼續處理下一個機器人。
3.最後,按position順序返回stack 中的健康度即可。
程式碼(JavaScript)
function survivedRobotsHealths(positions: number[], healths: number[], directions: string) : number[] {
//用一個棧存放當前存活的機器人
let stack: robot[] = [];
interface robot {
i: number;
p: number;
h: number;
d: string;
}
let robots: robot[] = [];
//從左至右(排序後的下標)遍歷機器人並判斷當前機器人的方向
positions.forEach((v, i) = >robots.push({
i: i,
p: v,
h: healths[i],
d: directions[i]
}));
robots.sort((a, b) = >a.p - b.p);
for (let i = 0; i < robots.length;) {
/**比較與棧頂元素的健康度,判斷存活哪個:
1.如果棧頂存活,棧頂機器人健康度減 1,繼續處理下一個機器人;
2.如果當前存活,棧頂彈出,當前機器人健康度減 1,回到 2.3 ;
3.如果兩個都消失,棧頂彈出,繼續處理下一個機器人。**/
if (stack.length === 0 || robots[i].d === 'R' || (robots[i].d === 'L' && stack[stack.length - 1].d === 'L')) {
stack.push(robots[i++]);
} else if (stack[stack.length - 1].h === robots[i].h) {
stack.pop();
i++;
} else if (stack[stack.length - 1].h > robots[i].h) {
stack[stack.length - 1].h--;
i++;
} else if (stack[stack.length - 1].h < robots[i].h) {
stack.pop();
robots[i].h--;
}
}
// console.log(stack);
stack.sort((a, b) => a.i - b.i); let ans = []; stack.forEach(v=> ans.push(v.h)); return ans;
};
最低票價
問題:
在一個火車旅行很受歡迎的國度,你提前一年計劃了一些火車旅行。在接下來的一年裡,你要旅行的日子將以一個名為 days 的陣列給出。 每一項是一個從 1 到 365 的整數。
火車票有 三種不同的銷售方式 :
- 一張 為期一天 的通行證售價為 costs[0] 美元;
- 一張 為期七天 的通行證售價為 costs[1] 美元;
- 一張 為期三十天 的通行證售價為 costs[2] 美元。
通行證允許數天無限制的旅行。 例如,如果我們在第 2 天獲得一張 為期 7 天 的通行證,那麼我們可以連著旅行 7 天:第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。 返回 你想要完成在給定的列表 days 中列出的每一天的旅行所需要的最低消費 。
範例 1:
輸入:days = [1,4,6,7,8,20], costs = [2,7,15]
輸出:11
解釋: 例如,這裡有一種購買通行證的方法,可以讓你完成你的旅行計劃: 在第 1 天,你花了 costs[0] = $2 買了一張為期 1 天的通行證,它將在第 1 天生效。 在第 3 天,你花了 costs[1] = $7 買了一張為期 7 天的通行證,它將在第 3, 4, ..., 9 天生效。 在第 20 天,你花了 costs[0] = $2 買了一張為期 1 天的通行證,它將在第 20 天生效。 你總共花了 $11,並完成了你計劃的每一天旅行。
範例 2:
輸入:days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
輸出:17
解釋: 例如,這裡有一種購買通行證的方法,可以讓你完成你的旅行計劃: 在第 1 天,你花了 costs[2] = $15 買了一張為期 30 天的通行證,它將在第 1, 2, ..., 30 天生效。 在第 31 天,你花了 costs[0] = $2 買了一張為期 1 天的通行證,它將在第 31 天生效。 你總共花了 $17,並完成了你計劃的每一天旅行。
提示:
- 1 <= days.length <= 365
- 1 <= days[i] <= 365
- days 按順序嚴格遞增
- costs.length == 3
- 1 <= costs[i] <= 1000
解決思路

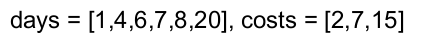
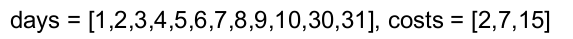
程式碼(JavaScript)
1.暴力遞迴解法:
//暴力遞迴解法
function mincostTickets(days: number[], costs: number[]) : number {
return costday(days, costs, 1);
};
function costday(days: number[], costs: number[], day: number) : number {
if (day > days[days.length - 1]) {
return 0;
}
if (day == days[days.length - 1]) {
return Math.min(...costs);
}
if (!days.includes(day)) {
return costday(days, costs, day + 1);
} else {
return Math.min( costday(days, costs, day + 1) + costs[0], costday(days, costs, day + 7) + costs[1], costday(days, costs, day + 30) + costs[2], )
}
};
問題:
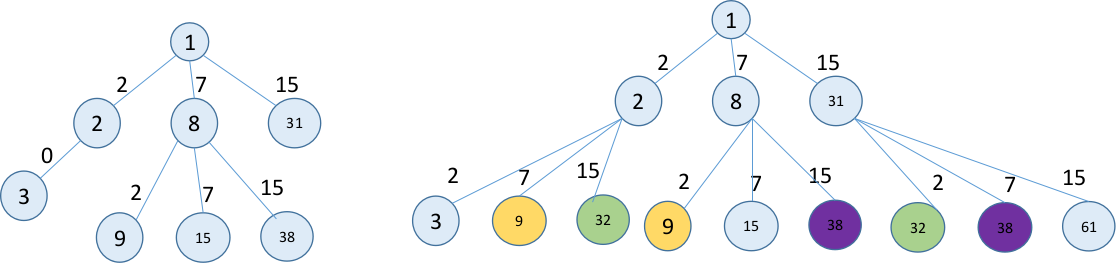
此解法存在重疊子問題和最優子結構
重疊子問題就是F(n)會重複計算,上圖中同色的結點
最優子結構就是F(n)的解,可以由子問題F(n+1),F(n+7),F(n+30)的解得到
解決方案:
記錄每個子問題f(n)的解,如果後面的計算又要用f(n),則直接取計算結果,避免重複計算:
function mincostTickets(days: number[], costs: number[]) : number {
let fn = [];
return costday(days, costs, 1, fn);
};
function costday(days: number[], costs: number[], day: number, fn: number[]) : number {
if (day > days[days.length - 1]) {
return 0;
}
if (day == days[days.length - 1]) {
if (!fn[day]) { fn[day] = Math.min(...costs);
}
return fn[day];
}
if (!days.includes(day)) {
if (!fn[day]) { fn[day] = costday(days, costs, day + 1, fn);
}
return fn[day];
} else {
if (!fn[day]) { fn[day] = Math.min( costday(days, costs, day + 1, fn) + costs[0], costday(days, costs, day + 7, fn) + costs[1], costday(days, costs, day + 30, fn) + costs[2], )
}
return fn[day];
}
};
2.動態規劃,自底向上解法
將前面的F(n)換為dp[n],表示從第n天開始後,總共的花費,dp[1]即是問題的解,F(n)是從前往後算,dp是從後往前算,消除遞迴。
function mincostTickets(days: number[], costs: number[]) : number {
const lastDay = days[days.length - 1];
let dp = new Array(lastDay + 30 + 1).fill(0);
for (let i = lastDay; i >= 1; i--) {
if (days.includes(i)) {
//此處還可以優化,將所有days放到set中判斷day是否存在
dp[i] = Math.min(dp[i + 1] + costs[0], dp[i + 7] + costs[1], dp[i + 30] + costs[2]);
} else {
dp[i] = dp[i + 1];
}
}
return dp[1];
};
總結
以上就是機器人碰撞和最低票價兩個問題的解法,除此之外,如果您想了解更多關於JavaScript的資料,歡迎存取這篇學習指南,無論是初學者還是有經驗的專業人士,該幫助手冊都將為您提供有價值的指導和幫助。
擴充套件連結: