貝塞爾曲線文字路徑

譯者注

這篇文章原本是之前翻譯 《曲線藝術程式設計》系列第八章--貝塞爾曲線一章中參照的內容

作者提到過知識點可參考這篇文章以及優化和線性插值所以我也時分想仔細看一篇

在當時其實開啟看過一眼，其中有看到導數部分，當時就怕翻譯錯了，所以我回頭抽空複習了一下數學的導數部分。說實話，畢業後的工作與生活中從未用到過導數

畢竟我只是個小前端，而非搞圖學的。寫寫 UI 之類的真用不到導數相關的知識

不過仔細想想

其實以前看過一些開發遊戲相關的書籍中其實一直都有高等數學相關的知識，只是自己選擇性的忽略了，畢竟只是泛泛的看。

高中的導數我複習過了，反正應該能理解翻譯這篇文章了。

對了，提醒一下，原文是 2009 年 5 月 29 號 要實的現文字效果確實需要這項技術

現在是 2023 年 ... 實現的效果其實現在我們在 web 用 svg 的 textPath 很容易實現

但原理還是很值得學習的

以下是譯文開始

背景

不久前，我對文字特效比較好奇，探索的其中之一便是將文字延曲線排列實現類似擦除的特效。

為此我弄了個原型，嘗試不同的解決方案。這篇文章記錄了一此通用解決方案，作為我的工作回顧。

這些記錄的解決方案可作為實現類似效果的工作手冊。

我最開始用的是 C# 和 GDI+ 實現，當然這一實現方法也適用於其它框架。

彎曲的文字

給定一些任意的樣條曲線，如何延曲線將文字繪製在上面且吸引人

期望實現的效果

在網上找了一圈，發現實現例子比較少，大部分實現的很糙，比如將字母單獨延曲線進行線性旋轉變幻，這樣實現的結果非常生硬，不流暢。

更好的實現方法被收集在了一篇 1995 年的老文章內，作者是 ~Don Lancaster, 比較特殊的一點是非線性圖形變幻（Nonlinear Graphic Transforms）。

牢記在這一領域我們是站在巨人的肩膀上。非常感謝 Don 這些年產出的非常優質且易理解的知識。

向量文字

一般來講要用 GDI+ 繪製文字，大部分人首先想到的就是 Graphics.DrawString() 類似這樣的 API, 它可以用於提供字一個符串傳進圖形上下文(Graphics context)。結果是一堆畫素資訊，對於非線性變形沒啥用處。

更好的方式是獲取渲染文字包含可用於形變點的外邊形向量，可用於形變成我們期望的效果。幸運的是 GraphicsPath 提供了此功能方法，即便 API 比較彆扭。

幫助我們理解 GraphicsPath 的一點是：GraphicsPath 是一個標準化的顯示列表，持有非常少的向量元資訊。

就 GraphicsPath 而言它不關注畫素資訊, 直到它用 Pens 或 Brushes 渲染。

事實上，以下就是我們會用到的 GraphicsPath 後設資料的完整列表：

• Start: 定義路徑起始點

• Line: 線條。包含結束點，最後一條指令起始點作為最後一個點。

• Bezier: 三階貝塞爾曲線

• Bezier3： 二階貝塞爾曲線

• CloseSubpath: 用於子路徑的閉合

• PathMarker: 定義一條路徑的標記，只是標記了資訊並不用於渲染

• DashMode: 是否虛線模式渲染

當使用 GraphicsPath 進行繪製時，跟顯示相關的方法僅有兩個：線條和貝塞爾曲線。注意 MSDN 檔案混淆了二階與三階樣條曲線（想象一下! 官方檔案居然進行錯誤引導）。

在實際使用中，在 GraphicsPath 上從未用到過二階樣條曲線（Bezier3）

其它形狀怎麼辦？在最後橢圓可以被新增進 GraphicsPath， 它應該有橢圓後設資料對吧？錯！，如果一個橢圓被新增進了 GraphicsPath, 在內部它會用數條貝塞爾樣條曲線模擬實現。

那麼使用 GraphicsPath 新增文字呢？再次的，它會被簡化為一堆點，線條，和貝塞爾曲線。這些都直接來源於字型描述，它也是基於向量的。

比較好的一件事是在 GraphicsPath 內一堆繪製，可通過迭代獲取內部用於繪製的完整的描述資訊。

有了這些元資訊就可重建這條路徑。在處理過程中，這些點可用一些形變操作達到文字纏繞效果。

文字被新增進 一個 GraphicsPath 然後渲染出來且沒有填充
所有這條路徑的點被標記為紅色(包含用於樣條的控制點)

貝塞爾曲線

在此我第一次嘗試，我決定使用貝塞爾樣條定義文字的路徑。GDI+ 支援三階貝塞爾， 圖形物件上有一些用於繪製的方法， 為數不多中的一個可用於獲取後設資料。

貝塞爾公式計算比較簡單，它們可被用於摸擬其它曲線，通過控制點建立一條貝塞爾曲線練習獲取一堆延貝塞爾曲線的點資訊比較容易。更復雜的圖形/曲線稍後會有。

獲取貝塞爾曲線上的一個點 GDI+ 並未提供，所以搞懂三階貝塞爾公式在此是必須的。我並不打算講解背後的大量數學細節。此課題在Wikipedia 和其它地方有大量的資料可供查詢。

貝塞爾曲線公式

好了，數學時間到！大多數貝塞爾曲線的幾何形成圖形應該像以下圖

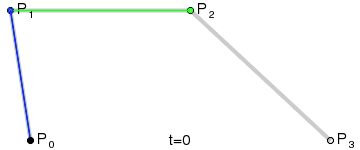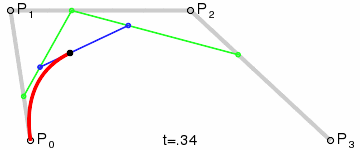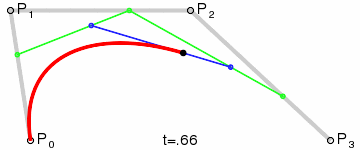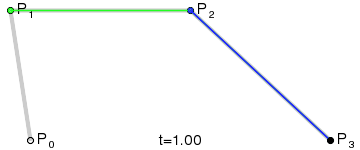
The geometric construction of a cubic Bézier (image from Wikipedia)

曲線由 P0-P3 共 4 個點控制。第一個和最後一個是曲線的起始與結束點， 另兩個是點通常被稱為 「手柄」 用於控制曲線形狀。

四個點被連線成三條線斷(圖中灰色線)。

在控制點連線形成的線段上的三個點由引數 t 插值形成，在上面構成了兩條綠色線斷。

最後一條藍色線斷由前兩條綠色插值線與 t 同樣方式產生。

最後一個點是延最後這條線斷插值產生，且這個點就 曲線 t 值 對應曲線上的點

兩個標量之間的線性插值如下：

vlerp = v0 + ( v1 - v0 ) * t 

可用寫個 2 個 2D 點之間的線性插值方法：

lerp(P0, P1, t) :
    xlerp = x0 + ( x1 - x0 ) * t 
    ylerp = y0 + ( y1 - y0 ) * t 
    return point (xlerp, ylerp)

上面的幾何圖形就可被以下方式表達：

P4 = lerp(P0, P1, t);
P5 = lerp(P1, P2, t);
P6 = lerp(P2, P3, t);
P7 = lerp(P4, P5, t);
P8 = lerp(P5, P6, t);
P9 = lerp(P7, P8, t);

P9 就是曲線上 t 對應的點

貝塞爾曲線也可被表達為8個係數的三階多項式方程：（稍後我會解釋如何通過計算從4個控制點獲取8個係數）

x = At3 + Bt2 + Ct + D 
y = Et3 + Ft2 + Gt + H 

讓 t 範圍從 0 到 1， 多項式會產生曲線上的一個 x, y 座標點。當值超範圍此方法還會在某處繼續產生無限的座標點。x 與 y 的版本公式非常相似，只是係數不同。

那麼 係數（A..H）從哪裡來的？完整的數學解釋在最後一節，現在我只會給出控制點轉換到係數的公式。

給定樣條 4 個控制點 P0 .. 03， 點的值為 (x0,y0) .. (x3,y3)，係數則是：

A = x3 - 3 * x2 + 3 * x1 - x0
B = 3 * x2 - 6 * x1 + 3 * x0
C = 3 * x1 - 3 * x0
D = x0

E = y3 - 3 * y2 + 3 * y1 - y0
F = 3 * y2 - 6 * y1 + 3 * y0
G = 3 * y1 - 3 * y0
H = y0

如果有必要從係數轉為控制點的話，下面是反轉操作：

x0 = D;
x1 = D + C / 3
x2 = D + 2 * C / 3 + B / 3
x3 = D + C + B + A

y0 = H;
y1 = H + G / 3
y2 = H + 2 * G / 3 + F / 3
y3 = H + G + F + E

為了說明到目前為止所涵蓋的內容，以下是一些虛擬碼，使用控制點 P0..P3:

// draw the Bézier using GDI+ function (g is Graphics object)
g.DrawBezier(Pens.Black,P0, P1, P2, P3);

// draw lines connecting the control points

g.DrawLine(redPenWithEndCap, P0,P1);
g.DrawLine(redPenWithEndCap, P2,P3);

[[compute coefficients A thru H as described above]]
[[用以上提到的方法計算出 A 到 H 係數]]

// draw 20 points, with a fixed increment for the parameter t
for (float t = 0; t <= 1; t += 0.05f)  
{
    x = At3 + Bt2 + Ct + D 
    y = Et3 + Ft2 + Gt + H 
    
    // call function that draws a filled rect at x,y coord.
    DrawBoxAtPoint(g, Color.Blue, x, y);  
}

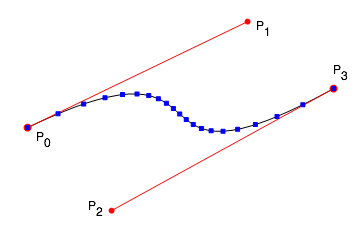
虛擬碼輸出黑色曲線，控制點由紅線連線，20個計算出的點標為了藍色

隨著 t 從 0 - 1， 這些點延曲線從起始點至結束點「散佈」 。如果用的點足夠多，它可以很好的模擬繪製出貝塞爾曲線。

事實上，在內部，很多圖形系統繪製貝塞爾曲線使用遞迴細分法，分割曲線至畫素級別或足夠小的短線繪製。

另一件值得關注的有趣的點是，儘管 t 的增長是定值的，根據它們處在曲線的位置,一些點卻比另一些靠的更近。

任意兩個連續的點與其它任意兩個點之間可能擁有不同的弧長 「arc-lengths」 (延曲線測量長度，而不是直線距離)。

可以把它想像成延曲線 「提速」 和 「減速」 時 rate 速率不同，這有助於幫助理解，儘管 t 值的增長是固定的。稍後還會再討論這點

切線和垂線

為了讓貝塞爾曲線公式應用於文字點， 這個 x 值必須首先格式化成 0..1 範圍，這樣才能被貝塞爾公式的 t 引數使用。

如果文字開始或接近 X 原點，且文字長度已知，則格式化非常簡單：

xnorm =  x / textwidth

文字的 Y 座標點需要從曲線上的點垂直投影(譯者注：相當於法線唄)。為了實現，需要通過 t 計算出一個曲線點對應的一個垂直向量。可以通過曲線上點的切線獲取，並將其旋轉 90 度。

計算貝塞爾的切線向量比較簡單，只要對貝塞爾多項式求導：

Vx = 3At2 + 2Bt + C 
Vy = 3Et2 + 2Ft + G 

我們可以通過線性代數對這個向量進行旋轉 90 度， 或更簡單的只需要互動這兩項並將其中一項取負值。

如果 V = (x, y) 那麼 Vrotate90 = (y, -x) 或 (-y, x), 具體用哪一種方式取決於你。

計算出一個向量垂直於貝塞爾曲線上一個點，這個點它由引數 t 求得。

在點的上面把垂直向量畫出來，像下圖這樣：

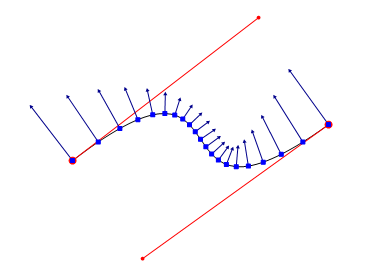
原始垂直向量. 為了繪製已經被縮短了. (末端還新增了小箭頭)

文字點的 Y 座標需要調整到垂直向量方向，但是這些向量的長度其實不重要，重要的是方向。為了方便垂直向量可以格式化為標準向量，讓它們都變為 1 單位的長度。一個向量擁有 x 和 y , 像下面這樣做即可：

magnitude = sqrt( x2 + y2 )  // 距離公式
x = x / magnitude
y = y / magnitude
// 注意：magnitude 為 0，則 x,y 也為 0 或 undefined

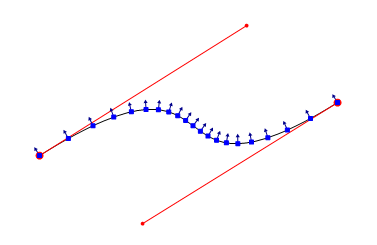
20 個格式化垂直向量，由引數 t 定義
為了繪圖，向量長度為 10 畫素

對於首次接觸使用貝塞爾曲線纏繞文字來說，這點數學知識足夠了

首試：伸縮文字

在纏繞文字上首次嘗試，給定貝塞爾控制點 P0..P3，還有圖形上下文 g 繪製：

string text = "Some text to wrap";

[[ Calculate coefficients A thru H from the control points ]]

GraphicsPath textPath = new GraphicsPath();

// the baseline should start at 0,0, so the next line is not quite correct
path.AddString(text, someFont, someStyle, someFontSize, new Point(0,0));

RectangleF textBounds = textPath.GetBounds();
 
for (int i =0; i < textPath.PathPoints.Length; i++)
{
    PointF pt = textPath.PathPoints[i];
    float textX = pt.X;
    float textY = pt.Y;
    
    // normalize the x coordinate into the parameterized value
    // with a domain between 0 and 1.
    float t =  textX / textBounds.Width;  
       
    // calculate spline point for parameter t
    float Sx = At3 + Bt2 + Ct + D 
    float Sy = Et3 + Ft2 + Gt + H 
        
    // calculate the tangent vector for the point        
    float Tx = 3At2 + 2Bt + C 
    float Ty = 3Et2 + 2Ft + G 
    // rotate 90 or 270 degrees to make it a perpendicular
    float Px =   Ty
    float Py = - Tx
    
    // normalize the perpendicular into a unit vector
    float magnitude = sqrt(Px2 + Py2)
    Px = Px / magnitude
    Py = Py / magnitude
    
    // assume that input text point y coord is the "height" or 
    // distance from the spline.  Multiply the perpendicular vector 
    // with y. it becomes the new magnitude of the vector.
    Px *= textY;
    Py *= textY;
    
    // translate the spline point using the resultant vector
    float finalX = Px + Sx
    float finalY = Py + Sy
    
    // I wish it were this easy, actually need 
    // to create a new path.
    textPath.PathPoints[i] = new PointF(finalX, finalY);
}

// draw the transformed text path		
g.DrawPath(Pens.Black, textPath);

// draw the Bézier for reference
g.DrawBezier(Pens.Black, P0,  P1,  P2,  P3);

用控制點虛擬碼生成的結果

看起來不錯，但還存在一些問題。文字中間擠在一起了，邊上又比較鬆散。牢記 arc-length 在點之間是變化的，即便 t 增加是定死的。

我將通過 定增的 t 新增一些點，並蓋在方向向量上用於顯示它們是如何用於纏繞文字的：

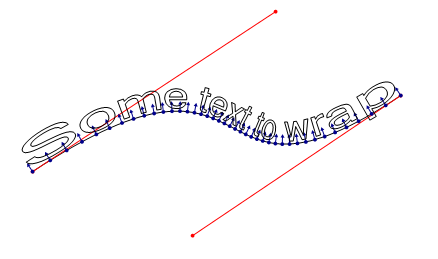
如圖貝塞爾的公式 arc-length 是非引數化的，問題就在於此。

當引數 t 定增時，計算得出的前後點之間 arc-lengths 是變化的。

貝塞爾的公式的這一特點，導致了文字在曲線上產生擠壓或拉伸的效果。

此外演演算法還有另一個問題：文字總是被擠壓或拉伸， 如下所示：

由於直接從0..1範圍對映文字被擠壓

由於直接從 0..1 範圍對映文字被拉伸

我們期望更好的效果是引數 t 對映至文字 x 軸座標不要試圖將文字填滿完整的貝塞爾曲線。為了實現這一目的， 曲線的 弧長 必須是已知的。問題又回到了起點。

解決文字長度問題（計算貝塞爾曲線長度）

解決提出的第二點問題（文字長度）比較簡單，如果曲線的 弧長已知。

相比於對映文字真實寬度 0..1 對應到 t ，文字可以先繪製進「邊界盒」（譯者注：通常圖形計算中的 AABB 中的 BB），邊界盒的寬度是樣條曲線的 弧長， 然後盒子的 x 座標通過除以所有 弧長 的 x 座標值後被縮放至 0..1。看圖更容易理解：

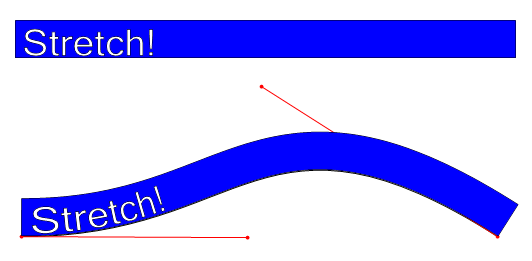
上圖的貝塞爾曲線 arc-length （弧長） 為 500 個單位，即邊界盒的寬度也要 500 個單位（上半部分藍色的）是為文字準備的，並縮放到 0..1 範圍。

邊界盒就像則以某種方式纏繞到了曲線上

在樣條曲線上超出邊界框部分的文字會被剪除掉。

然後，遺留的問題就剩如何計算貝塞爾曲線的 弧長了。在經過一翻研究後，我發現很明顯沒有一個標準的解決方案。

模擬 弧長的方法非常多，有一些解決方案涉及中等複雜度的微積分。而且最複雜和最精確的解決方案涉及迭代逼近法。

然而，有一種非常簡單的估算 弧長方法：基於定增的 t 將曲線分割成一堆線段，然後統計所有線段的長度。它產生的結果是分割的越小，得到的模擬估算越準，它運用了貝塞爾曲線的特徵輸出點靠的越近曲線越平滑。

一些經驗調查表明大約 100 份的分割僅會產生小於 0.001 的估算錯誤，這僅是 500 畫素長的曲線的一半。用於我們手頭的這點兒活來說精度足夠了。

處理過程可以被視覺化成在貝塞爾曲線上面畫多條線段：

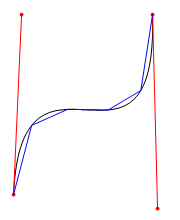
用藍色的 4 段線去估算弧長精度不夠

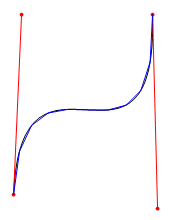
用 8 段的話精度就高多了

虛擬碼非常簡單。有許多可優化之處，但基礎的演演算法足夠高效了，只要分割數不要太大。

int numberOfDivisions = 100;
int maxPoint = numberOfDivisions + 1;

// _formula.GetPoint(t) 通過 t 獲取點座標
// 點通過貝塞爾公式計算

PointF previousPoint = _formula.GetPoint(0);  // 曲線起點

float sum = 0;

for (int i = 1; i <= maxPoint; i++)
{
    PointF p = _formula.GetPoint( i / (float) maxPoint );
    sum += distance(previousPoint, p);
    previousPoint = p;
}

// 計算兩點距離的方法:
float distance(PointF a, PointF b) { return sqrt( (bx - ax)2 + (by - ay)2 ); }

該程式碼可以很容易地被通用化到任何連續的單值引數化演演算法，它擁有固定的範圍，返回多個點，比如橢圓公式或其它不同型別的樣條曲線。

估算誤差並動態地選擇一個「理想的」除數是可能的。這可以通過細分來完成，直到線段長度低於某個閾值，或者通過比較線段的切線和曲線的切線，但我沒有探索這兩種想法。

我用固定數 100 似乎對當前的目的足夠有效。

弧長引數化

即使文字寬度問題解決後，由於在標準化 t 值之間弧長還沒有被標準化 文字被擠壓和拉伸的問題還是存在。

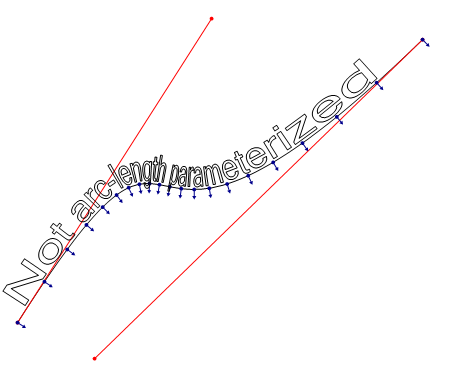
該圖說明了弧長引數化的缺乏。這個問題獨立於另一個問題，但有一個相關的解決方案。
(垂直向量旋轉了180°，因此不會被遮擋)

解決該問題的方法被稱為孤長引數化。其思想是將一個輸入值 u 對映到貝塞爾公式的引數 t 上，並且將產生對於 u 一樣標準化的等距弧長的點。

換句話說，若 u 的值是 0..1 ，它將對映到 t 的值，通過此方法產生的某個點值就是弧長距離起點的某個分數值。

舉個例子，u 值如果為 0.25 , 它將總是會返回整條曲線弧長距離的 1/4。在此例中中間值 t 還是未知，必須通過某種對映方法計算得到。

我使用的實現方法（基於數學比我更好的朋友的建議）是 用一張孤長表近似。它儲存了我們已討論過的孤長公式計算的所有弧長。如果某條曲線弧長為 500，分為 100 份，表格將會顯示如下：

  0.0
  5.2
 10.5
 15.7 
 ... (more points) ...
494.8
500.0

值索引對應引數 t 的某個值，如果列表包含了 101 個值，索引 0 包含了 t = 0.0 時的弧長， 索引 100 對應了 t=1.0 時孤長， 索引 50 對應了 t=0.5 時孤長。

如果表被存放在了名為 arcLength 的陣列中，索引對應的 t 值即：

t = index / (float) (arcLengths.Length - 1)

有了這樣一張表格，找到 t 對應的孤長就成為了可能。通過獲取輸入值 u ， 計算期望的弧長( u * totalArcLength)，然後在表中找到輸入值對應的最大值，值大小於等於希望的弧長。可以用簡單的遍歷或更好的二分搜尋。

如果恰好值等於弧長，輸入值 u 對應的 t 值可以按之前那樣算。通常情況下，找到的最大值會小於期望的弧長。在這種情況下，線性插值被用於輸入值與下一個值之間估算 t 值。

假設使用了足夠大的除數來建立表，那麼這些點之間的距離將足夠小，對映的誤差可以忽略不計

以下的虛擬碼將演示這項技術：

float u = // 引數值 u , 範圍 0 到 1 之間
float t; // 通過 u 要尋找的 t

float [] _arcLengths = // 預先計算好的貝塞爾曲線弧長列表

// u 對應的目標弧長
float targetArcLength = u * _arcLengths[ _arcLengths.Length - 1 ];

// 二分搜尋
int index = IndexOfLargestValueSmallerThan(_arcLengths, targetArcLength)

// 如果精確匹配，返回基於精確 index 的 t
if (_arcLengths[index] == targetArcLength)
{
    t = index / (float) (arcLengths.Length - 1);
}
else  // 否則需要在兩個點之間插值
{
    float lengthBefore = _arcLengths[index];
    float lengthAfter = _arcLengths[index+1];
    float segmentLength = lengthAfter - lengthBefore; // 兩個點之間的距離

    // 決定在「前」和「後」點之間的位置
    float segmentFraction = (targetLength - lengthBefore) / segmentLength;
                          
    // add that fractional amount to t 
    // 加上額外的這部分分數 segmentFraction 給 t
    t = (index + segmentFraction) / (float) (_arcLengths.Length -1);
}

這個基本演演算法可以封裝成通用的類用於處理弧長估算。以下就是使用此對映演演算法生成的圖，表現好多了:

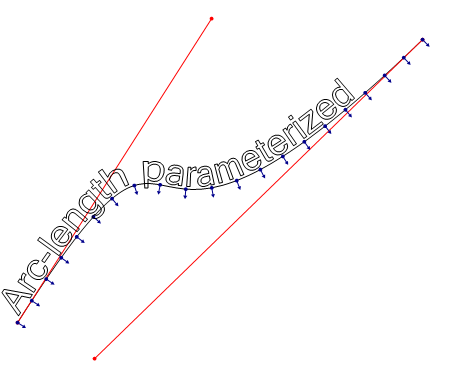
在弧長引數化後，注意標準化 u (標成藍色的)現已均分在曲線上。（垂直向量旋轉了 180 度以不被遮擋）

解決其它一些小問題

此演演算法仍然不完美。尤其是在長的水平線段在環繞在比較尖的曲線時字元會產生扭曲。除了最嚴重的情況外，這個問題可以通過迭代文字路徑時將長線段分成更短的線段來解決。

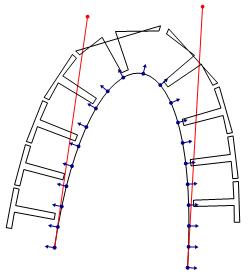
字母 'T' 頂部有一條單獨的橫線，由於它處在比較尖的曲線部分它未能彎曲，

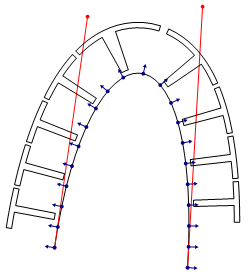
將線段分割成足夠的小犧牲一部分效能的情況下可以改善顯示效果

在一些例子中，這項技術可以從使用較短的貝塞爾曲線代替長的貝塞爾曲線中受益。然而，簡單的使用貝塞爾曲線替換所有的線段是不夠的，一些長線段上使用效果並不太好。

這就作為練習留給讀者去尋找答案了

擴充套件至更復雜的路徑

此項技術可以很簡單的擴充套件到更復雜的任意路徑。所要做的就是計算整條路徑的弧長(通過累計所有部分的弧長)，並全部引數化。

可將公式封裝成類，其包含了多種子路徑，並可以通過對總長度的反向插值來決定對特定引數使用哪個子路徑，或者可以整合到弧長估算公式內。

文字在任意路徑上的纏繞效果

這產生了一個潛在的新問題，特別是文字纏繞在另一個文字路徑上。斷點（路徑停止點並重新開始往另外一處），如果字元或其它物件跨越這些點可能引起嚴重的錯亂。

一個通用的演演算法需要考慮到這些，並且確保以合適方式處理這些問題，比如將字母推過這些斷點處。很多字元包含了銳角彎曲和看起來效果不怎麼好的過度包裹的邊角（如上圖所示）也得要處理

總結

此項扭曲文字（任意路徑）的技術能得到相對自然流暢的顯示效果。此演演算法允許曲線可以被實時計算表示，即使是在低端的現代硬體上。為了簡化講解，許多優化手段在此文中沒有討論。此技術可輕易的適用於任何擁有向量路徑物件的圖形框架(比如WPF，Cocoa,Postscript, 等)。巧妙的使用扭曲的向量路徑可以用於有趣的美學效果

---

原文 ~Warping Text to a Bézier curves

---

部落格園: http://cnblogs.com/willian/
github: https://github.com/willian12345/