紅黑樹(Red Black Tree)

紅黑樹（Red Black Tree）是一種自平衡二叉查詢樹，是一種高效的查詢樹，學習之前先了解一下平衡二元樹。於 1972 年由 Rudolf Bayer發明的對稱二叉B 樹演化而來，並以 2-3-4 樹、2-3 樹流行。最終在 1978 年由Leonidas J.Guibas 和 Robert Sedgewick 從對稱二叉 B 樹中推匯出紅黑樹。紅黑樹具有良好的效率，它可在 O(logN) 時間內完成查詢、增加、刪除等操作

建立在 BST 二元搜尋樹的基礎上，AVL、2-3 樹、紅黑樹都是自平衡二元樹，紅黑樹每個節點增加了一個儲存位，用來記錄節點的顏色，RED或者BLACK 。但相比於 AVL ，高度平衡所帶來的時間複雜度，紅黑樹對平衡的控制要寬鬆一些，紅黑樹只需要保證黑色節點平衡即可。也正因紅黑樹在插入和刪除時不需要太多的平衡操作，也讓它成為 Java 中 HashMap 底層的資料結構、Linux 的 CFS 進行排程演演算法、多路複用技術的 Epoll 等各類底層的資料結構實現。

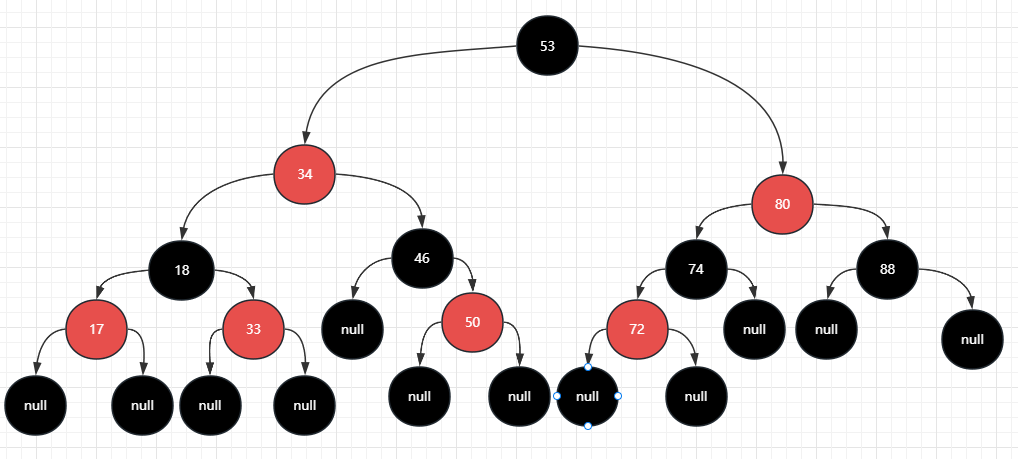
實際上，在紅黑樹中真正被定義為葉子結點的，是那些空節點，如上圖

五大性質

性質1：每個節點要麼是紅色，要麼是黑色。
性質2：根節點是黑色。
性質3：每個葉子節點（NIL節點或null）都是黑色。
性質4：如果一個節點是紅色的，則它的兩個子節點都是黑色。也就是說，不能有兩個連續的紅色節點。
性質5：對於每個節點，從該節點到其所有後代葉子節點的簡單路徑上，包含相同數量的黑色節點。

紅黑樹保證最長路徑不超過最短路徑的二倍，因而近似平衡（最短路徑就是全黑節點，最長路徑就是一個紅節點一個黑節點，當從根節點到葉子節點的路徑上黑色節點相同時，最長路徑剛好是最短路徑的兩倍）

2-3樹

理解紅黑樹之前要先了解一下2-3樹，因為它們都是依靠旋轉進行調衡樹高的，上面講的五條性質，就是根據2-3樹演變而來的，不然沒有原因，來的就有些突然。

2-3 樹是一種樹型資料結構，由約翰·霍普克洛夫特於 1970 年發明。它通過在個節點存放 1-2個元素來平衡樹高。從而也使 2-3 樹存在2 叉節點和3 叉節點

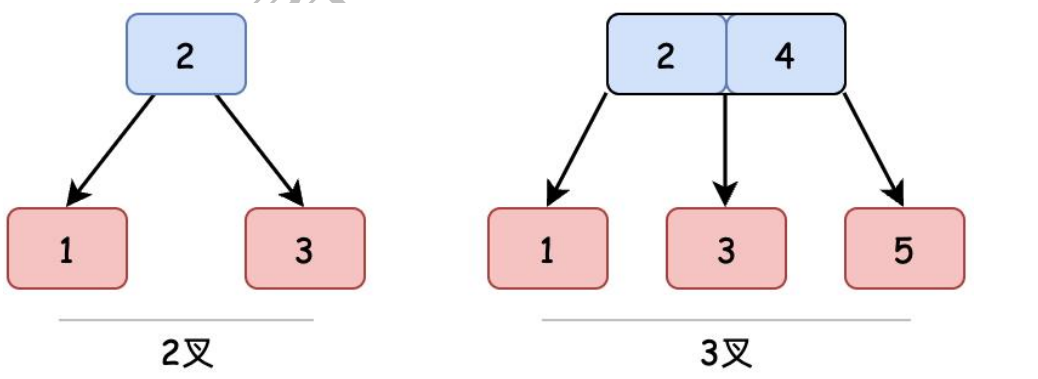
其中每個具有子節點（內部節點）的節點要麼有兩個子節點（2 節點）和一個資料元素，要麼有三個子節點（3 節點）和兩個資料元素。另外 2-3 樹是 3 階 B 樹，2-3-4 樹是 4 階 B 樹。

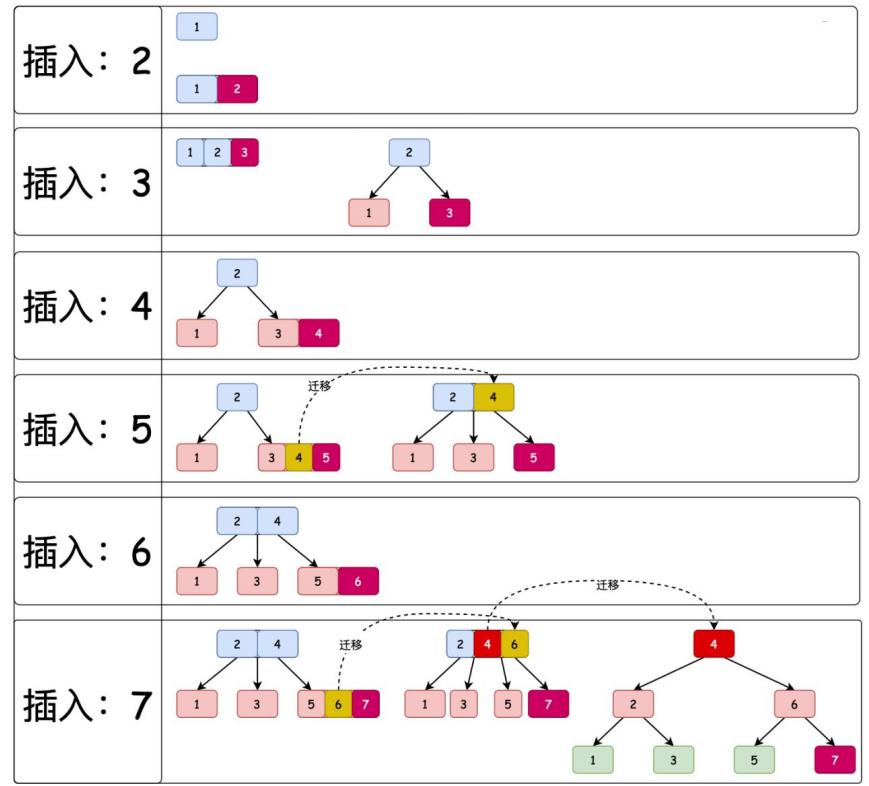
在 2-3 樹中順序插入 1、2、3、4、5、6、7，七個元素時，2-3 樹的調衡處理

2-3 樹的插入過程與 BST 樹類似，會通過樹的左右節點大小，找到自己的插入位置
一個節點可以有 1-3 個元素，但當元素個數為 3 時，則需要調衡。把三個節點的中間節點晉升上來，其餘兩個節點為子節點。
如果進行一次調衡後，上一層父節點達到 3 個元素，則需要 2 次調，來滿足 2-3樹的規則。

拆分節點

當一個節點內有 3 個元素的時候，就要發起拆分東西，拆分的過程分為;

對 3 個節點的中間節點，插入到父節點上
剩餘 2 個節點建立出新的節點。
建立父節點和新建立的 2 個節點間關係

2-3樹和紅黑樹的關係

上面這顆紅黑樹，我們來將所有的紅色節點上移到和他們的父節點同一高度上，就會形成如下結構

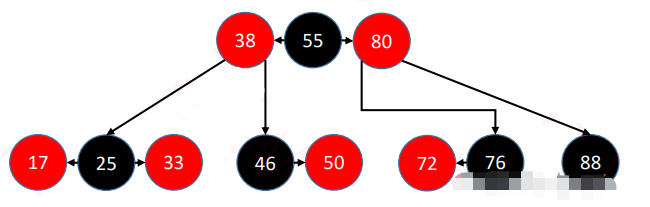
這個結構很明顯，就是一棵四階B樹

紅黑樹和 4階B樹（2-3-4樹）具有等價性
黑色節點與它的紅色子節點融合在一起，形成1個B樹節點
紅黑樹的黑色節點個數與 4階B樹的節點總個數相等
在所有的B樹節點中，永遠是黑色節點是父節點，紅色節點是子節點。黑色節點在中間，紅色節點在兩邊。

操作

這裡就不做過多講解插入和刪除的具體細節，感興趣的可以去看看CSDN上的一篇文章，是結合2-3樹進行介紹的；還有簡書上一篇窮舉了紅黑樹插入和刪除的各種細節。什麼情況下需要染色，什麼情況下需要旋轉還是很有必要知道的，這篇文章就從這裡講起

左傾染色

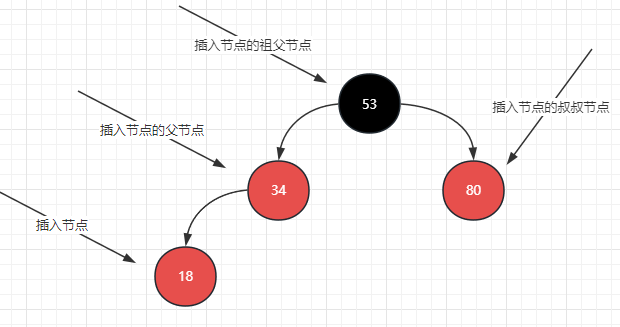
新增節點 1，相當於 2-3 樹中在節點 2 上新增了一個節點，這個時候並不影響樹高，只需要染色保持紅黑樹的規則即可。染色過程如圖所示。

新增節點1，父親節點和叔叔節點都是紅色
把父節點染黑、叔叔節點染黑，爺爺節點染紅
爺爺節點染紅是臨時的，這時候試想爺爺節點是根節點，不滿足性質2，又會把爺爺節點染黑

右傾染色

新增節點 4，相當於 2-3 樹中在節點 3 上新增了一個節點，這個時候並不影響樹高，只需要染色保持紅黑樹的規則即可。染色過程如圖所示。

1.和上面的左旋染色過程一樣，只是方向變了

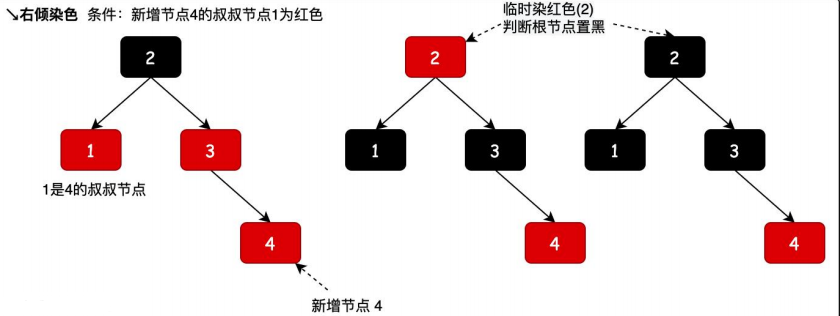
左旋調衡

對照 2-3 樹，只有當一個節點內有 3 個節點的時候，才需要調衡。那麼紅黑樹則是判斷當前節點的叔叔節點是否為紅色節點，如果不是則沒法通過染色調衡，也

就是需要選擇進行調衡

1 左旋一次

這種情況屬於插入節點的父節點是紅色，但叔叔節點是黑色或空（NIL）需要進行 染色 + 左旋 操作來修復平衡

當你把紅黑樹對照理解成 2-3 樹，如圖中第 1 步驟下的左側小圖，新增的節點 5 倒置 2-3 樹不平衡
那麼這個時候需要把 2-3 樹中節點 4 提起來，而對應紅黑樹則需要先進行染色，待操作的節點 4 為黑色，兩個孩子節點為紅色。
最後是把節點 3 進行一次左旋操作，完成樹的平衡。對應步驟 3 中的左側小圖是 2-3樹調衡後的結果

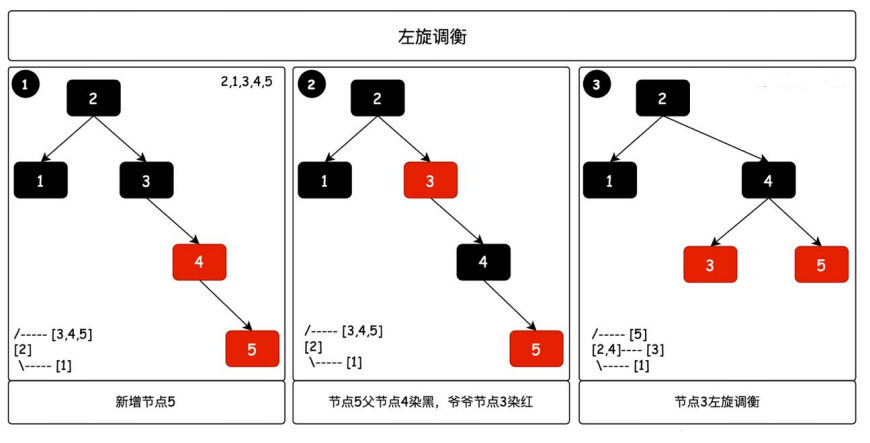
2 右旋 + 左旋

當一次左旋沒法調衡，需要右旋+左旋的情況，在 AVL 樹中有同樣的場景。本身樹需要左旋操作，但整體分支樹節點偏左，此時需要右旋調整樹結構再左旋。可以參考平衡二元樹中的旋轉

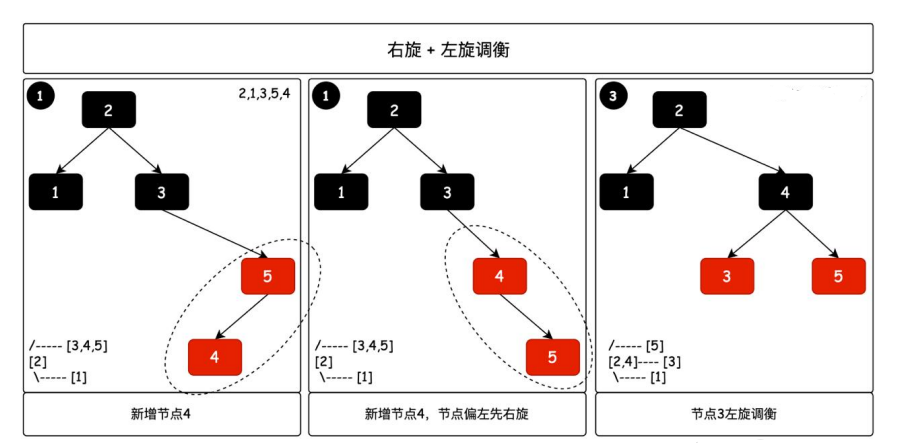
紅黑樹新增節點 4 以後，4→5 結構偏左，需要先進行右旋調衡樹結構，再進行左旋。

其實這個時候再進行的左旋就和上面一次左旋操作一致了

右旋調衡

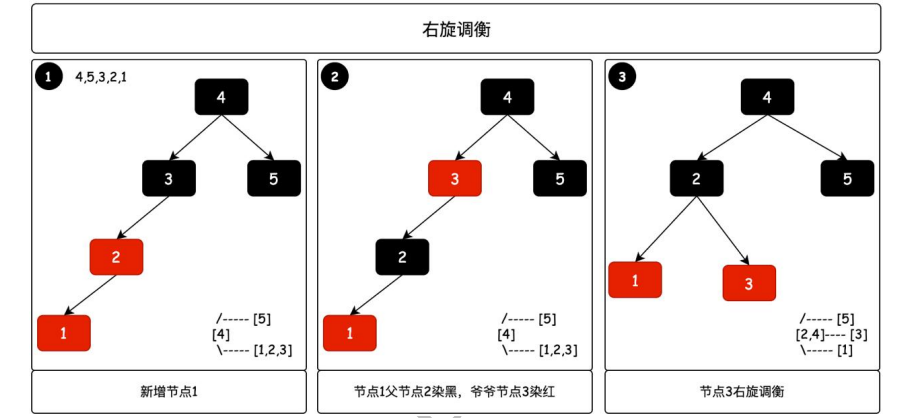
1 一次右旋

對照 2-3 樹，只有當一個節點內有 3 個節點的時候，才需要調衡。那麼紅黑樹則是判斷當前節點的叔叔節點是否為紅色節點，如果不是則沒法通過染色調衡，也就是需要選擇進行調衡。

當你把紅黑樹對照理解成 2-3 樹，如圖中第 1 步驟下的右側小圖，新增的節點 1 倒置 2-3 樹不平衡。
那麼這個時候需要把 2-3 樹中節點 2 提起來，而對應紅黑樹則需要先進行染色，待操作的節點 2 為黑色，兩個孩子節點為紅色。
最後是把節點 2 進行一次右旋操作，完成樹的平衡。對應步驟 3 中的右側小圖是 2-3樹調衡後的結果。

2 左旋 + 右旋

當一次左旋沒法調衡，需要左旋+右旋的情況，在 AVL 樹中有同樣的場景。本身樹需要右旋操作，但整體分支樹節點偏右，此時需要左旋調整樹結構再右旋。

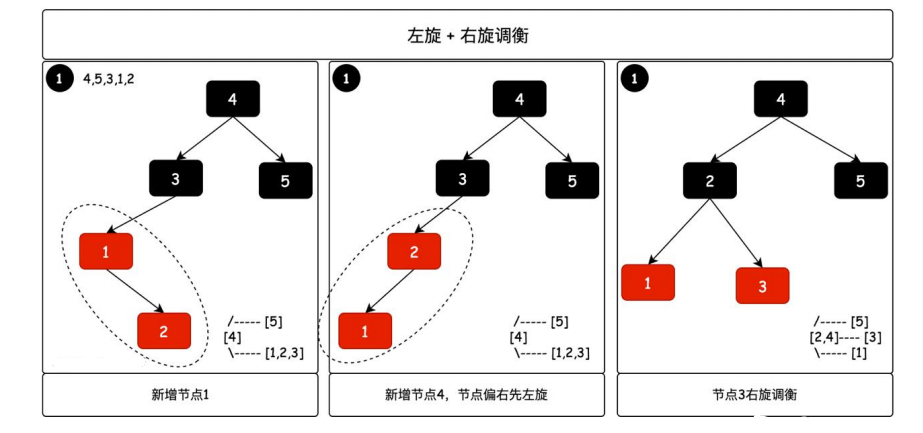
紅黑樹新增節點 2 以後，1↘2 結構偏右，需要先進行左旋調衡樹結構，再進行右旋。其實這個時候再進行的右旋就和上面一次右旋操作一致了。

總結

紅黑樹相對於普通的二元搜尋樹（BST）具有自平衡性，這意味著它在插入和刪除操作後會自動進行調整以保持平衡。這種自平衡性賦予了紅黑樹在特定應用中一些重要的優勢，使其更適合解決某些問題。以下是紅黑樹相對於普通BST的一些用途和優勢：

平衡性保證：紅黑樹的平衡性確保了樹的高度保持在較低水平，使得各種操作的平均時間複雜度為O(log n)，這包括插入、刪除和查詢操作。在高度平衡的情況下，紅黑樹能夠提供可靠的效能。
插入和刪除操作高效：由於紅黑樹能夠自動調整以保持平衡，插入和刪除節點的操作通常具有可接受的效能。這對於需要頻繁更新資料的應用非常有用，如資料庫系統。
範圍查詢：紅黑樹非常適合範圍查詢，因為它們具有排序性質，可以輕鬆找到在某一範圍內的所有節點。這在資料庫查詢和檔案系統中很有用。
多執行緒和並行：由於紅黑樹的自平衡性和性質保證，它們在多執行緒環境中表現出色。在並行資料結構中，紅黑樹通常用於實現各種同步機制，如鎖、佇列等。
記憶體分配：在某些作業系統和程式語言中，紅黑樹用於記憶體分配演演算法，例如Linux的slab allocator就使用了紅黑樹來管理記憶體塊。
檔案系統：許多檔案系統使用紅黑樹來維護檔案和目錄的結構，以提供高效的檔案查詢和管理。
資料庫系統：資料庫系統中的索引通常使用紅黑樹來加速資料查詢操作。例如，許多關係型資料庫管理系統（RDBMS）使用B+樹（一種變種的紅黑樹）來管理索引。
圖演演算法：紅黑樹的結構可以用於一些圖演演算法，如最短路徑演演算法，以提高效率。

平衡二元樹和紅黑樹的區別

平衡性維護：
- 紅黑樹：在紅黑樹中，平衡性是通過節點的顏色屬性來維護的，通過染色和旋轉操作來確保平衡性。這使得紅黑樹對於插入和刪除操作有一定的靈活性，可能會導致樹的高度相對較高。
- AVL樹：AVL樹是一種更為嚴格的平衡二元搜尋樹，它通過節點的平衡因子（左子樹高度減去右子樹高度）來維護平衡性。AVL樹的平衡要求更為嚴格，插入和刪除操作會更頻繁地導致樹的旋轉操作，以維持平衡，因此樹的高度相對較低，查詢操作更快。
效能差異：
- 紅黑樹：由於其相對較寬鬆的平衡性要求，紅黑樹在插入和刪除操作上比AVL樹更高效，但查詢操作可能會略微慢一些，因為紅黑樹的高度相對較高。
- AVL樹：AVL樹在查詢操作上非常高效，因為它的高度非常平衡，但在插入和刪除操作上更耗時，因為它需要頻繁地進行旋轉操作。
適用場景：
- 紅黑樹：適用於需要頻繁執行插入和刪除操作，而對查詢效能要求較低的場景。例如，檔案系統、資料庫索引、記憶體分配演演算法等。
- AVL樹：適用於需要快速查詢操作，並且能夠承受較慢的插入和刪除操作的場景。例如，編譯器中的符號表、排序演演算法、高頻查詢資料庫等。
記憶體消耗：
- 紅黑樹：通常比AVL樹具有較低的記憶體消耗，因為紅黑樹的平衡要求相對較寬鬆，節點不需要儲存額外的平衡因子。
- AVL樹：由於需要儲存平衡因子，AVL樹的節點可能會佔用更多的記憶體空間。

總之，紅黑樹在需要高效的插入、刪除和查詢操作，並且需要保持平衡性的場景下非常有用。它們在電腦科學和軟體工程中有廣泛的應用，尤其是在需要高效能和可靠性的領域。然而，需要注意的是，紅黑樹並不適用於所有情況，有時其他資料結構如雜湊表或AVL樹可能更適合特定的需求。選擇合適的資料結構應根據具體的應用場景和效能需求來決定。
本文並沒有使用程式碼實現紅黑樹，JDK中TreeMap的原始碼實現的更為優秀，兼顧各個方面，感興趣的可以看看