拉普拉斯金字塔在多圖HDR演演算法中的應用以及多曝光影象的融合演演算法簡介。

      在SSE影象演演算法優化系列二十九：基礎的拉普拉斯金字塔融合用於改善影象增強中易出現的過增強問題（一） 一文中我們曾經描述過基於幾種高頻融合法則的拉普拉斯金字塔融合演演算法，那裡是主要針對2副影象的。實際的應用中，我們可能會遇到多幀影象的融合過程（影象都是對齊後的），特別是多幀不同曝光度的影象的融合問題，在相機的應用中較為廣泛，我們同時也可以認為這是另外一種的HDR演演算法。 

      這方面最經典的文章是2007年Tom Mertens等人發表的《Exposure Fusion》一文，用簡單的篇幅和公式描述了一個非常優異的合成過程，雖然在2019年Charles Hessel發表了一篇《Extended Exposure Fusion》的文章中，提出了比Exposure Fusion更為優異的合成效果，但是代價是更高昂的計算成本，而Exposure Fusion也已經相當優秀了，本文主要簡單記錄下個人的Exposure Fusion優化過程。

　　Exposure Fusion的思路也非常之簡單，輸入是一系列影象對齊後的大小格式相同的影象，輸出是一張合成的多細節圖。那麼在進行計算之前，他需要做以下的準備。 

　　1、對每副影象按照某些原則計算每融合的權重。文章裡提出了3種權重。

　　   （1） 對比度：

               Contrast: we apply a Laplacian filter to the grayscale version of each image, and take the absolute value of the filter response [16]. This yields a simple indicator C for contrast. It tends to assign a high weight to important elements such as edges and texture. 

　　對應的matlab程式碼非常簡單：

% contrast measure
function C = contrast(I)
h = [0 1 0; 1 -4 1; 0 1 0]; % laplacian filter
N = size(I,4);
C = zeros(size(I,1),size(I,2),N);
for i = 1:N
    mono = rgb2gray(I(:,:,:,i));
    C(:,:,i) = abs(imfilter(mono,h,'replicate'));
end

　　我們可以認為就是個邊緣檢測。

　　（2）飽和度 

           Saturation: As a photograph undergoes a longer exposure, the resulting colors become desaturated and eventually clipped. Saturated colors are desirable and make the image look vivid. We include a saturation measure S, which is computed as the standard deviation within the R, G and B channel, at each pixel。

% saturation measure
function C = saturation(I)
N = size(I,4);
C = zeros(size(I,1),size(I,2),N);
for i = 1:N
    % saturation is computed as the standard deviation of the color channels
    R = I(:,:,1,i);
    G = I(:,:,2,i);
    B = I(:,:,3,i);
    mu = (R + G + B)/3;
    C(:,:,i) = sqrt(((R - mu).^2 + (G - mu).^2 + (B - mu).^2)/3);
end

　　也是非常簡單的過程。

　　（3）曝光度

　　　Well-exposedness: Looking at just the raw intensities within a channel, reveals how well a pixel is exposed. We want to keep intensities that are not near zero (underexposed) or one (overexposed). We weight each intensity i based on how close it is to 0.5 using a Gauss curve: exp - (i-0.5)*(i-0.5)/(2*σ *σ), where σ equals 0.2 in our implementation. To account for multiple color channels, we apply the Gauss curve to each channel separately, and multiply the results, yielding the measure E。

% well-exposedness measure
function C = well_exposedness(I)
sig = .2;
N = size(I,4);
C = zeros(size(I,1),size(I,2),N);
for i = 1:N
    R = exp(-.5*(I(:,:,1,i) - .5).^2/sig.^2);
    G = exp(-.5*(I(:,:,2,i) - .5).^2/sig.^2);
    B = exp(-.5*(I(:,:,3,i) - .5).^2/sig.^2);
    C(:,:,i) = R.*G.*B;
end

　　每副影象得到三個指標（對比度C、飽和度S以及曝光度E），將他們相乘得到這幅影象的綜合權重W。

     2、根據每副影象的權重，計算在序列中影象的每副影象的歸一化權重，原文表述如下：

          To obtain a consistent result, we normalizethe values of the N weight maps such that they sum to one at each pixel (i, j):      

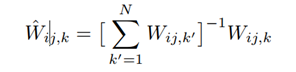
　　　注意，這是單個畫素進行的處理，也就是說對於一個序列的影象，每個對應畫素位置的權重先計算好後，再累加得到總權重，然後在每個對應畫素的權重除以總權重得到歸一化的值。

    3、理論上講，得到了這些權重，就可以對N個影象進行直接融合，即使用下述公式：

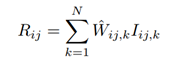
 　　但是如果真的這樣做，得到的結果慘不忍睹，即使我們對歸一化後的權重進行高斯模糊、保邊模糊等等也是解決不了問題的。所以這個文章的最核心的精華部分就在下面的過程中了。 

     4、我們並不是直接用這些權重進行合成，而是對原序列影象進行高斯拉普拉斯金字塔分解（利用其中的拉普拉斯資料），對各序列對應的歸一化權重做高斯金字塔分解。 然後重構拉普拉斯金字塔，重構的規則為：

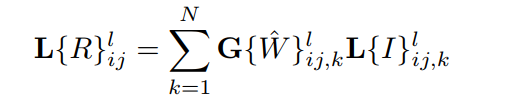
　　　　即對合成後各層拉普拉斯金字塔資料，用每個序列的權重的高斯金字塔資料乘以對應的拉普拉斯金字塔資料，然後累加。就如此簡單。

　　關於這個演演算法的原理性說明，CSDN這個作者講的也比較好： 【HDR】曝光融合（Exposure Fusion），有興趣可以參考。

　　這個演演算法的效果通過測試確實還是可以的，原始的作者提供了MATLAB版本的程式碼，但是實際測試速度是非常慢的，這個也不怪這些論文的作者，他們的重點是實現演演算法本身，而不是工程化。

　　為了能提高演演算法的實用性，我們使用C++結合SIMD指令對該過程進行優化。優化的方式主要有以下幾個方面：

       1、通過適當的改變資料型別來提高速度。

        M版本的程式碼是全程是使用的浮點型別的來計算各種資料的，為了效率，有些過程我們可以使用整形來代替。比如獲取各個特徵的權重的時，我們可以用byte來記錄就可以了。在比如金字塔的分解和重構時，高斯金字塔我們也用byte型別記錄，拉普拉斯金字塔考慮到有負數以及資料的範圍，可以用signed short型別來記錄。 

       2、通過改變資料型別後，使用對應的SIMD指令可以起到更大的步長，浮點數一般一次性只能處理4個數，如果是signed short則可以同時處理8個資料了。 

       3、對於金字塔分解和重構，要從原理上進行優化，詳見：SSE影象演演算法優化系列二十六:和時間賽跑之優化高斯金字塔建立的計算過程。

       我們以計算飽和的過程為例，看看SSE的優化步驟： 

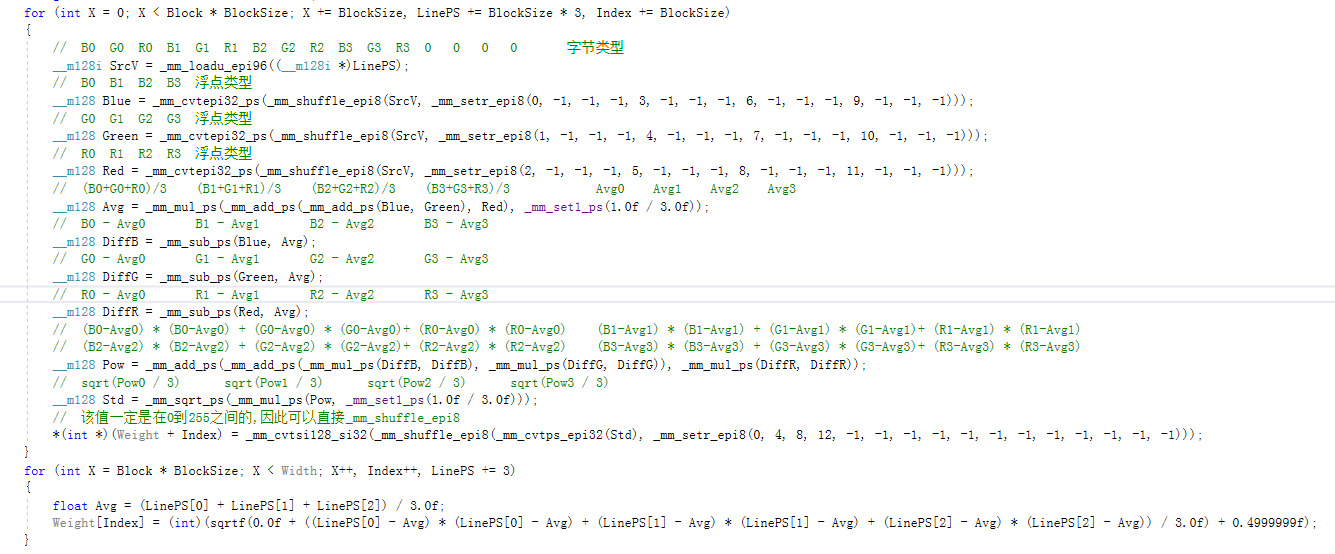
 　   簡簡單單的M程式碼，需要大概10倍以上行數的C程式碼和SIMD指令進行優化。 

　　實際上，我們在優化時，歸一化的那個權重矩陣我也用byte型別來儲存資料，原本以為這樣每個圖的權重有可能會比較小，存在精度損失，不過實際測試，和M程式碼的結果也沒啥特別大的視覺區別。 

　　另外，還有記憶體方面的優化問題，如果建立所有影象的金字塔序列，然後再計算特徵合成，這樣會佔用比較多的記憶體，特別是影象序列比較多時，實際上我們可以邊分解邊進行計算，這樣帶來的好處時速度有適當加速（應該還是cache miss較小的原因），當然如果每個序列都分配金字塔的記憶體，有一個好處就是，可以使用omp進行並行，適當的通過佔用資源提高速度。

　　原始論文的作者在獲取了各個特徵的權重後，是使用的乘法來統計特徵，我這裡也使用了加法進行測試，測試結果是加法的結果比乘法的要稍微暗一點。區別也不是很大，但是要注意如果是使用乘法，有的時候有些特徵的權重為0，為了不讓其他特徵的權重被淹沒掉，建議加一後再乘。 

　　效果：