聊聊神經網路的基礎知識
來自《深度學習入門:基於Python的理論與實現》
張量
Numpy、TensorFlow、Pytorch等框架主要是為了計算張量或是基於張量計算。
標量:0階張量;12,4,3,
向量:一階張量;[12,4,3]
矩陣:二階張量;[ [12,4,3], [11,2,3] ]
多階張量:多維陣列;
可以將張量的階度理解為多維陣列的維度。
神經網路
神經網路的圖表示:
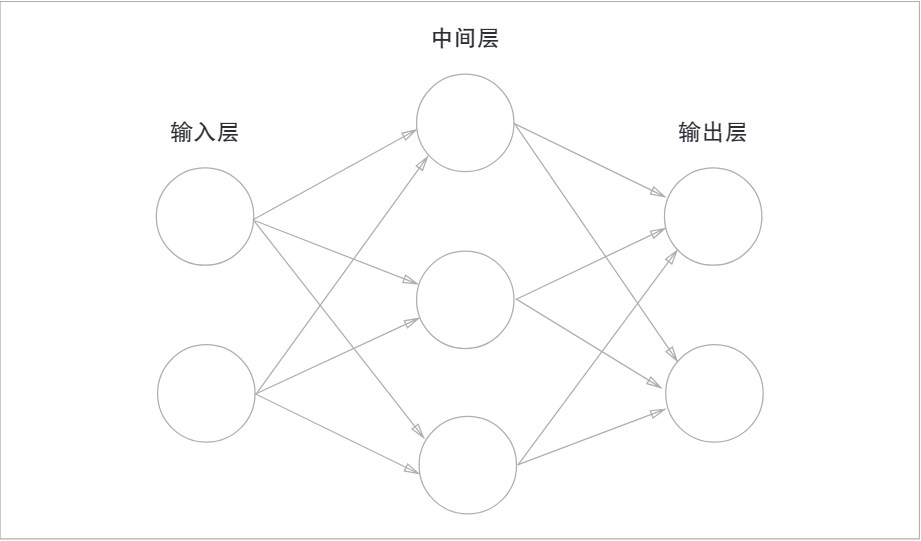
最左邊的一列稱為輸入層,最右邊的一列稱為輸出層,中間的稱為中間層,也叫做隱藏層。
啟用函數
概述
啟用函數的作用在於決定如何來啟用輸入訊號的總和。數學表示式如下:
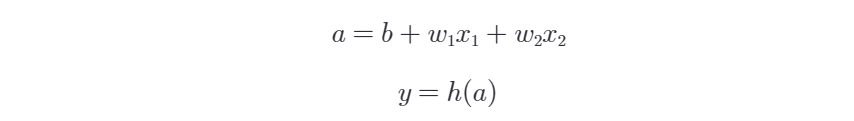
圖表示如下:
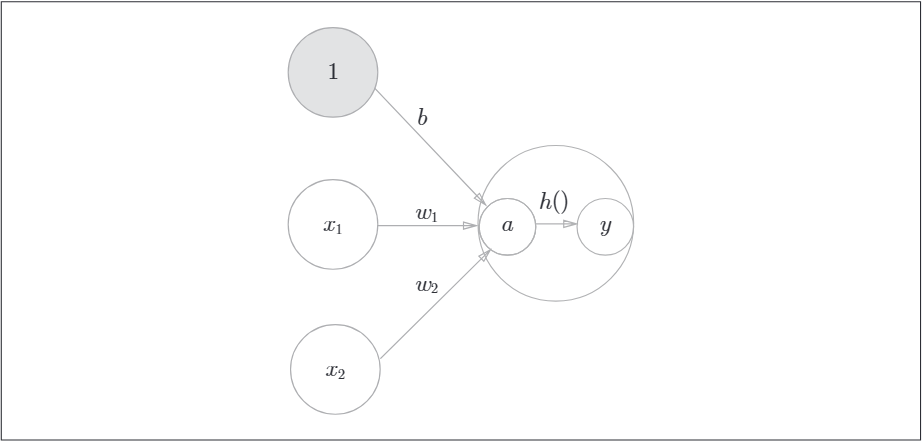
通常神經元用一個○表示,在明確神經網路的動作下,可以明確顯示啟用函數的計算過程。如下,這兩個圖是等效的。
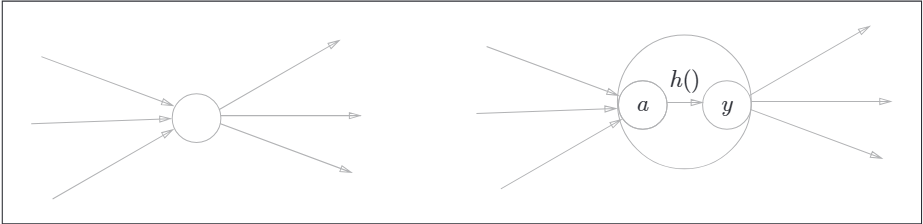
sigmoid函數
神經網路中用sigmoid函數作為啟用函數,進行訊號的轉換,轉換後的訊號被傳送到下一個神經元。
函數表示為:
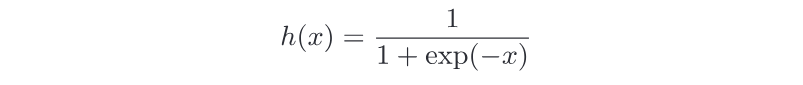
使用Numpy實現:
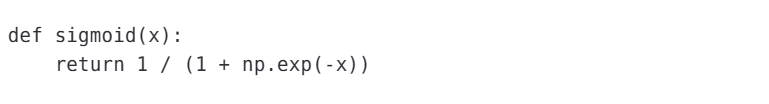
relu函數
relu函數在輸入大於0時,直接輸出該值;在輸入小於等於0時,輸出0。函數表示:
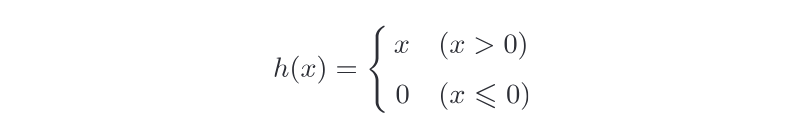
使用Numpy實現:

神經網路的實現
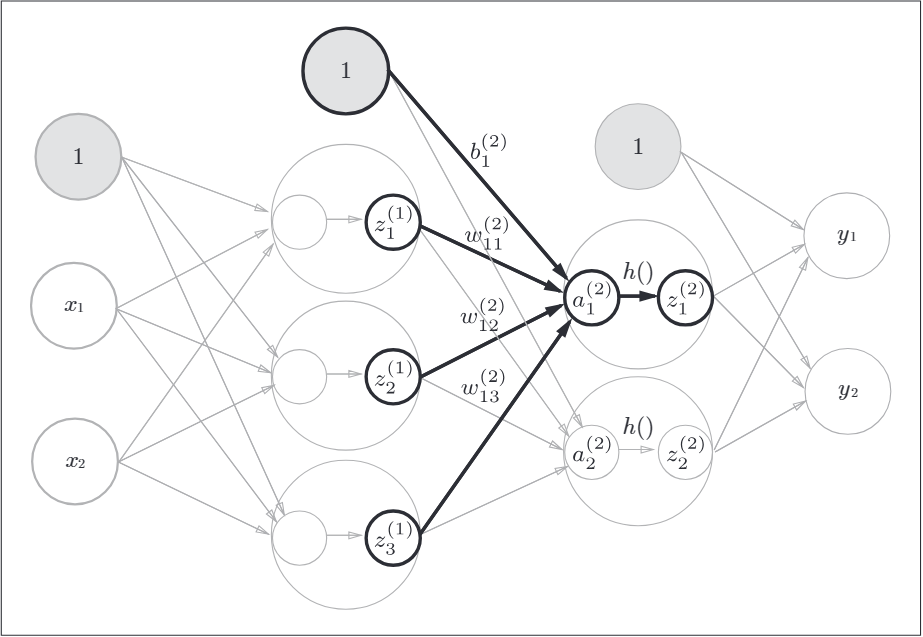
如下是三層神經網路的圖表示,第0層神經元到第一層神經元的訊號傳遞:
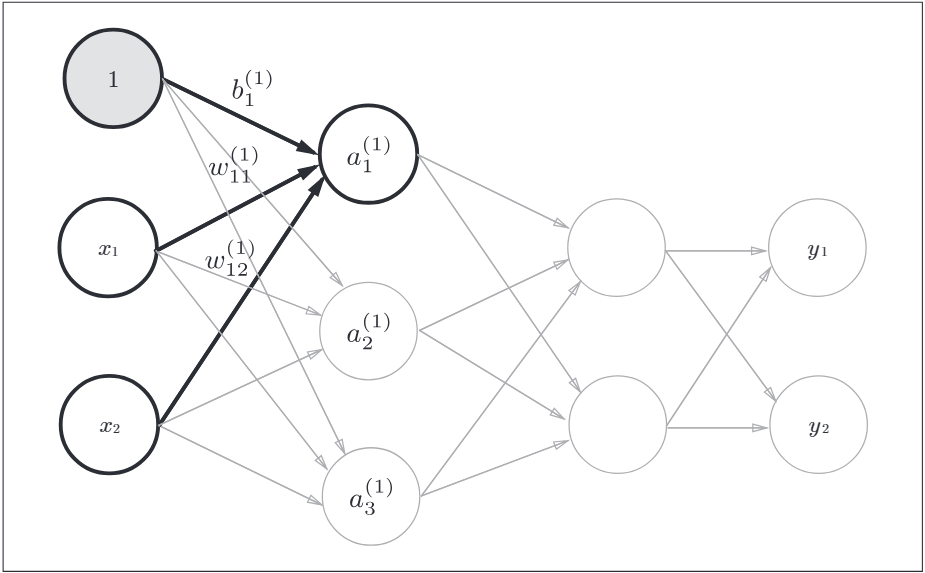
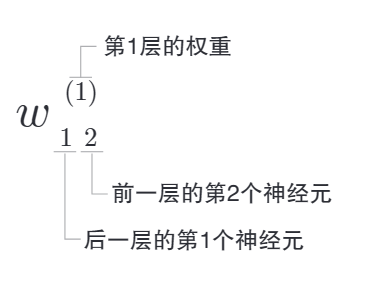
符號解釋:
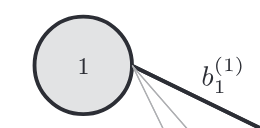
如下表示引入了偏置的神經元"1"。
神經元a1的數學表示式如下:
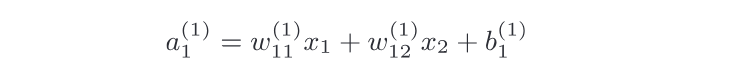
矩陣的乘法運算:
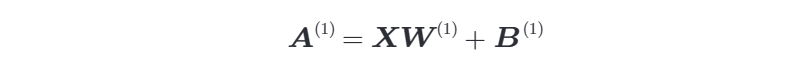
NumPy實現:


中間層(隱藏層)的啟用函數可能是不一樣的,如上可能是sigmoid函數或是rule函數計算。
第1層神經元到第二層神經元的訊號傳遞,從下圖也可以看出來,第二層到輸出層的訊號傳遞:
輸出層的設計
神經網路可以用在分類問題和迴歸問題上,不過需要根據情況改變輸出層的啟用函數。一般而言,迴歸問題用恆等函數,分類問題用softmax函數。
機器學習的問題大致分為分類問題和迴歸問題。分類問題是資料屬於哪一個類別的問題。而回歸問題是根據某個輸入預測一個數值的問題。
Affine層
Affine層(也稱為全連線層、線性層或密集層)是一種基本的神經網路層,其主要作用是將輸入資料與權重矩陣相乘並新增偏置,以進行線性變換。這個線性變換是神經網路中的重要組成部分,它將輸入資料對映到另一個空間,以便後續的非線性變換和學習。這可以用以下數學公式表示:
深度神經網路中,通常會有多個Affine層連線在一起,構成網路的一部分。每個Affine層將前一層的輸出作為輸入,並且可以具有不同的權重和偏置,以捕捉不同的特徵和複雜性。通常,在Affine層之後會新增非線性啟用函數(如ReLU、Sigmoid或Tanh),以使神經網路能夠捕捉更復雜的模式和特徵。這些非線性函數使神經網路能夠逼近任意複雜的函數。
恆等函數和softmax函數
恆等函數會將輸入按原樣輸出,對於輸入的資訊,不加以任何改動的直接輸出。神經網路圖表示:
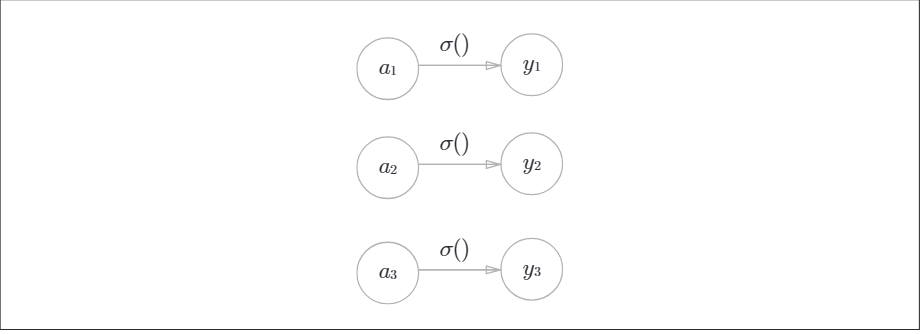
分類問題中的softmax函數,其數學表示式如下,計算第K個神經元的輸出:
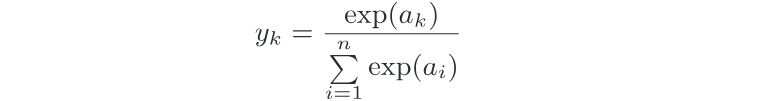
圖表示如下,輸出層的各個神經元都受到所有輸入訊號的影響:
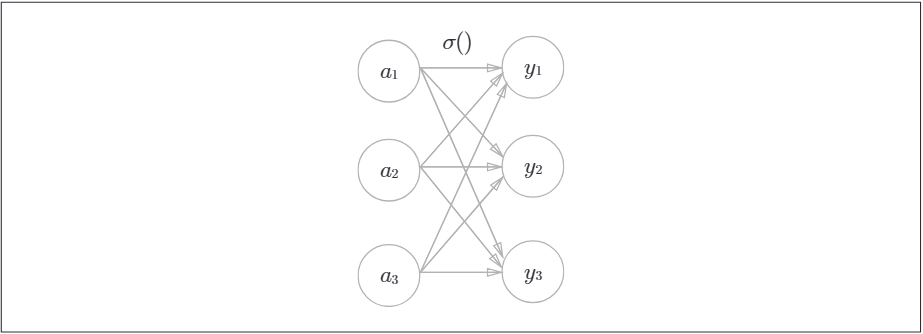
softmax函數的python實現:

softmax函數的輸出是0.0到1.0之間的實數。並且softmax函數的輸出值的總和是1。因此可以把softman函數的輸出解釋為"概率"。
比如在手寫數位識別時,Softmax層的輸出如下:
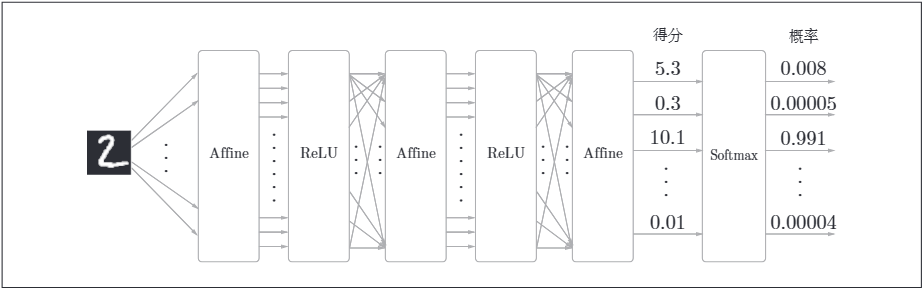
輸入影象經過Affine層與ReLU層進行轉換,10個輸入通過Softmax層進行正規化。在這個例子中,"0"的得分時5.3,這個值經過Softmax層轉換,輸出概率為0.008的值;"2"的得分時10.1,被轉換為0.991。
損失函數
損失函數標識神經網路效能的"惡劣程度"的指標,即當前的神經網路對監督資料在多大程度上不擬合,在多大程度上不一致。損失函數的計算可以使用均方誤差和交叉熵誤差。
折積神經網路
折積神經網路(CNN)增加了折積層(Convolution)和池化層(Pooling)。其神經網路結構範例如下:
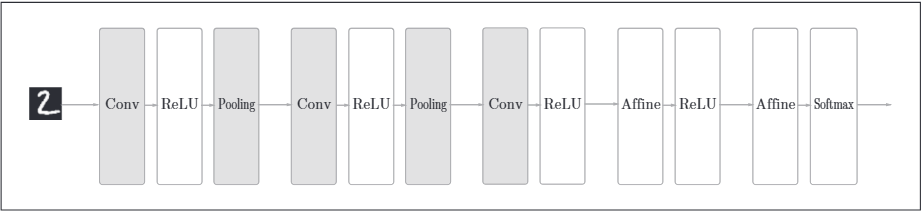
之前的全連線神經網路中忽略了資料的形狀,比如,輸入資料是影象時,影象通常是高、長、通道三個方向上的3維形狀。但是向全連線層輸入時,需要將3維資料拉平為1維資料。全連線層會忽視形狀,將全部的輸入資料作為相同的神經元(同一緯度的神經元)處理,所以無法利用與形狀相關的資訊。
而折積層可以保持形狀不變。當輸入資料是影象時,折積層會以3維資料的形式接受輸入資料,並以3維資料的形式輸出至下一層。因此,CNN架構的網路可以正確理解影象等具有形狀的資料。
折積層
折積層進行的處理就是折積運算。折積運算相當於影象處理中的"濾波器運算"。如下範例:
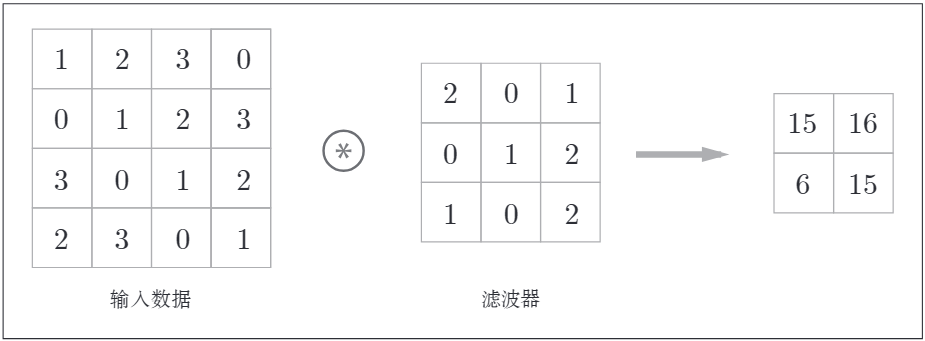
折積運算對輸入資料應用濾波器。計算順序如下,折積運算以一定間隔的步幅滑動濾波器的視窗並應用。如下所示:
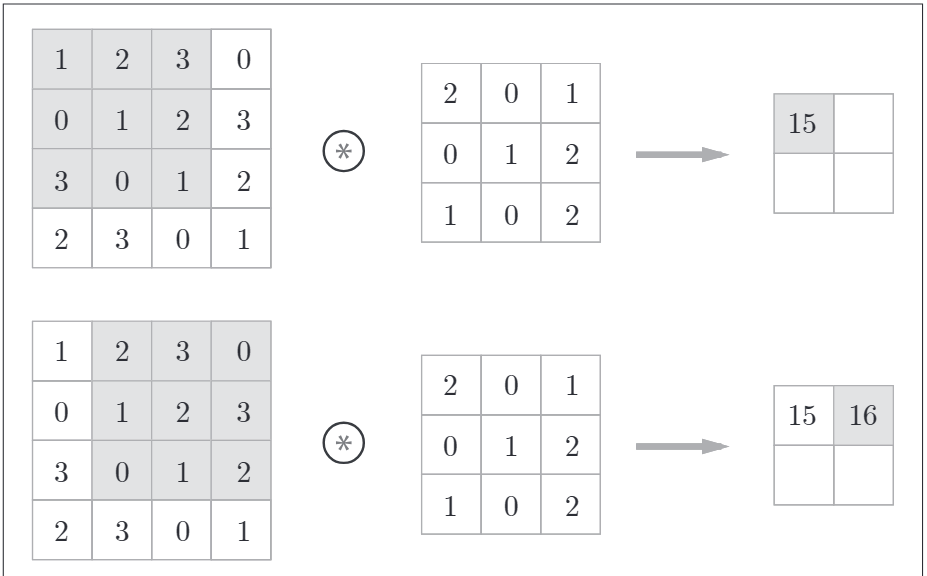
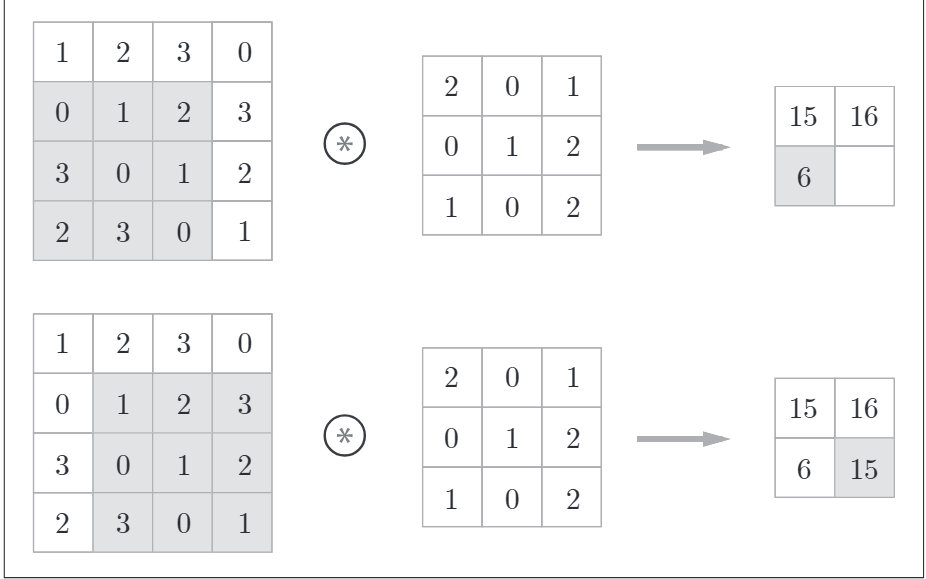
將各個位置上濾波器的元素與輸入的對應元素相乘,然後再求和。最後將結果儲存到輸出的對應位置。將這個過程在所有的位置運算一遍,就可以得到折積運算的輸出。
3維資料的折積運算
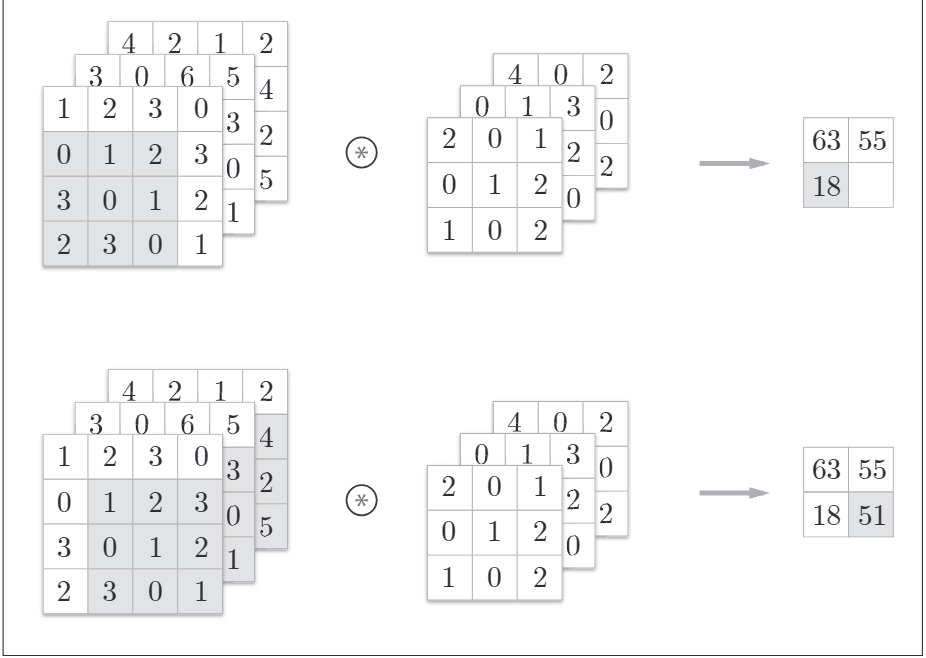
之前的折積運算都是以高、長方向的2維形狀為物件的。影象是3維資料,除了高、長方向還有通道方向。增加了通道,會按通道進行輸入資料與濾波器的折積運算。如下是增加了通道方向的3維資料進行折積運算的例子:
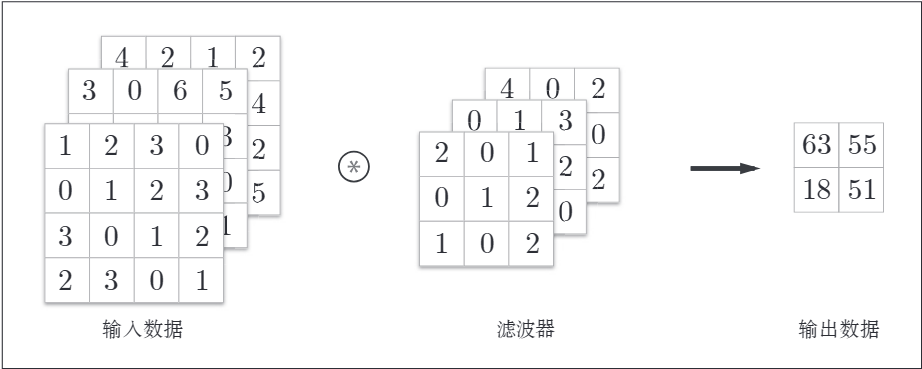
計算順序如下:
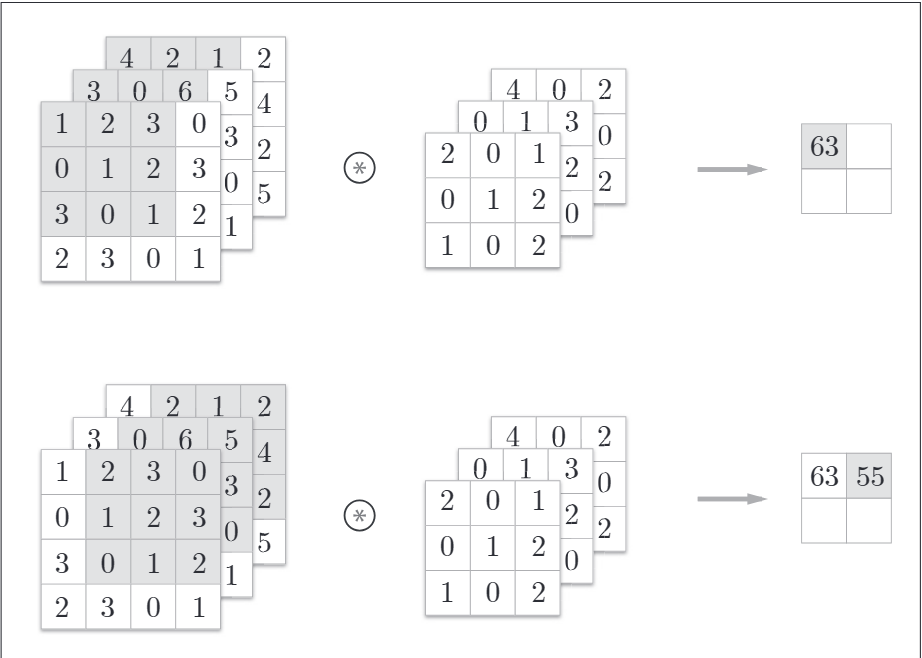
池化層
池化是縮小高、長方向上的空間的運算。如下,將2*2的區域集約成1個元素的處理,縮小空間大小。