Java實現常見查詢演演算法
Java實現常見查詢演演算法
查詢是在大量的資訊中尋找一個特定的資訊元素,在計算機應用中,查詢是常用的基本運算,例如編譯程式中符號表的查詢。
線性查詢
線性查詢(Linear Search)是一種簡單的查詢演演算法,用於在資料集中逐一比較每個元素,直到找到目標元素或搜尋完整個資料集。它適用於任何型別的資料集,無論是否有序,但在大型資料集上效率較低,因為它的時間複雜度是 O(n),其中 n 是資料集的大小。
以下是線性查詢的基本步驟:
- 從資料集的第一個元素開始,逐一遍歷每個元素。
- 比較當前元素與目標元素是否相等。
- 如果相等,表示找到了目標元素,返回當前元素的索引位置。
- 如果不相等,繼續遍歷下一個元素。
- 如果遍歷完整個資料集都沒有找到目標元素,則返回一個表示元素不存在的標識(如 -1)。
以下是使用Java實現線性查詢的範例程式碼:
public class LinearSearch {
public static int linearSearch(int[] arr, int target) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == target) {
return i; // 目標元素的索引位置
}
}
return -1; // 目標元素不存在於陣列中
}
public static void main(String[] args) {
int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = linearSearch(arr, target);
if (result == -1) {
System.out.println("目標元素不存在於陣列中");
} else {
System.out.println("目標元素的索引位置為: " + result);
}
}
}
二分查詢
二分查詢演演算法(Binary Search)是一種高效的查詢演演算法,用於在有序陣列或列表中查詢特定元素的位置。它的基本思想是通過將陣列分成兩半,然後確定目標元素在哪一半,然後繼續在那一半中搜尋,重複這個過程直到找到目標元素或確定不存在。
二分查詢演演算法的時間複雜度是 O(log n),其中 n 是資料集的大小。這使得它在大型有序資料集中的查詢操作非常高效,每次將資料集分成兩半,然後確定目標元素在哪一半,然後繼續在那一半中搜尋。每次操作都將資料集的規模減少一半,因此它的時間複雜度是對數級別的.
需要注意的是,二分查詢演演算法要求資料集必須是有序的。如果資料集無序,需要先進行排序操作。排序操作通常具有較高的時間複雜度(如快速排序的平均時間複雜度為 O(n log n)),因此總體上二分查詢演演算法加上排序操作的時間複雜度可能會更高。
總結起來,二分查詢演演算法是一種高效且常用的查詢演演算法,在大型有序資料集中具有較低的時間複雜度。
以下是二分查詢演演算法的詳細步驟:
- 初始化左指標
left為陣列的起始位置,右指標right為陣列的結束位置。 - 計算中間位置
mid,即mid = left + (right - left) / 2。 - 比較中間位置的元素與目標元素:
- 如果中間位置的元素等於目標元素,則返回中間位置。
- 如果中間位置的元素大於目標元素,則更新右指標
right = mid - 1,並回到步驟2。- 如果中間位置的元素小於目標元素,則更新左指標
left = mid + 1,並回到步驟2。
- 如果中間位置的元素小於目標元素,則更新左指標
- 如果左指標大於右指標,則表示目標元素不存在於陣列中。
以下是使用Java實現二分查詢演演算法的範例程式碼(迭代法):
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
int left = 0;// 左指標,初始為陣列起始位置
int right = arr.length - 1;// 右指標,初始為陣列結束位置
while (left <= right) {
int mid = left + (right - left) / 2; // 計算中間位置
if (arr[mid] == target) { // 如果中間位置的元素等於目標元素,則找到目標元素
return mid;
} else if (arr[mid] < target) { // 如果中間位置的元素小於目標元素,則在右半部分繼續查詢
left = mid + 1;
} else { // 如果中間位置的元素大於目標元素,則在左半部分繼續查詢
right = mid - 1;
}
}
return -1; // 目標元素不存在於陣列中
遞迴法
public class BinarySearchRecursive {
public static int binarySearch(int[] arr, int target, int left, int right) {
if (left <= right) {
int mid = left + (right - left) / 2;// 計算中間位置
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {// 如果中間位置的元素小於目標元素,則在右半部分繼續查詢
return binarySearch(arr, target, mid + 1, right);
} else {// 如果中間位置的元素大於目標元素,則在左半部分繼續查詢
return binarySearch(arr, target, left, mid - 1);
}
}
return -1; // 目標元素不存在於陣列中
}
public static void main(String[] args) {
int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = binarySearch(arr, target, 0, arr.length - 1);
if (result == -1) {
System.out.println("目標元素不存在於陣列中");
} else {
System.out.println("目標元素的索引位置為: " + result);
}
}
}
如果陣列中有多個相同的目標元素,上面的演演算法只會返回其中一個的索引位置,可以優化一下返回全部元素的下標
// 迭代
public static List<Integer> binarySearchAllIterative(int[] arr, int target) {
List<Integer> indices = new ArrayList<>();
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
indices.add(mid);
// 向左掃描找到所有相同元素的索引
int temp = mid - 1;
while (temp >= 0 && arr[temp] == target) {
indices.add(temp);
temp--;
}
// 向右掃描找到所有相同元素的索引
temp = mid + 1;
while (temp < arr.length && arr[temp] == target) {
indices.add(temp);
temp++;
}
break; // 結束迴圈,避免重複掃描
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return indices;
}
// 遞迴
public class BinarySearchMultiple {
public static List<Integer> binarySearchAll(int[] arr, int target) {
List<Integer> indices = new ArrayList<>();
binarySearchAllRecursive(arr, target, 0, arr.length - 1, indices);
return indices;
}
public static void binarySearchAllRecursive(int[] arr, int target, int left, int right, List<Integer> indices) {
if (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
indices.add(mid); // 將找到的索引加入列表
// 繼續在左半部分和右半部分繼續查詢相同目標元素的索引
binarySearchAllRecursive(arr, target, left, mid - 1, indices);
binarySearchAllRecursive(arr, target, mid + 1, right, indices);
} else if (arr[mid] < target) {
binarySearchAllRecursive(arr, target, mid + 1, right, indices);
} else {
binarySearchAllRecursive(arr, target, left, mid - 1, indices);
}
}
}
}
通常情況下,迭代法比遞迴法的效率要高。這是因為迭代法避免了函數呼叫的開銷,而函數呼叫涉及堆疊管理、引數傳遞等操作,會導致一定的效能損耗。此外,迭代法通常更容易優化,可以通過使用迴圈不斷更新變數的方式來進行計算,從而更有效地利用計算資源。
插值查詢
插值查詢演演算法是一種基於有序陣列的搜尋演演算法,類似於二分查詢,但它在選擇比較的元素時使用了一種更為精細的估計方法,從而更接近目標元素的位置。插值查詢的基本思想是根據目標元素的值與陣列中元素的分佈情況,估算目標元素在陣列中的大致位置,然後進行查詢。
在二分查詢中,mid的計算方式如下:
將low從分數中提取出來,mid的計算就變成了:
在插值查詢中,mid的計算方式轉換成了:
low 表示左邊索引left, high表示右邊索引right,key 就是target
插值查詢演演算法的步驟如下:
- 初始化左指標
left為陣列的起始位置,右指標right為陣列的結束位置。 - 使用插值公式來估算目標元素的位置:
pos = left + ((target - arr[left]) * (right - left)) / (arr[right] - arr[left])
其中,target是目標元素的值,arr[left]和arr[right]分別是當前搜尋範圍的左邊界和右邊界的元素值。 - 如果估算位置
pos對應的元素值等於目標元素target,則找到目標元素,返回位置pos。 - 如果估算位置
pos對應的元素值小於目標元素target,則說明目標元素在當前位置的右側,更新left = pos + 1。 - 如果估算位置
pos對應的元素值大於目標元素target,則說明目標元素在當前位置的左側,更新right = pos - 1。 - 重複步驟 2 到步驟 5,直到找到目標元素或搜尋範圍縮小到無法繼續搜尋為止。
插值查詢的優勢在於當陣列元素分佈均勻且有序度較高時,其效率可以比二分查詢更高。然而,當陣列元素分佈不均勻或有序度較低時,插值查詢可能會導致效能下降,甚至變得不如二分查詢。
需要注意的是,插值查詢演演算法的時間複雜度通常為 O(log log n),但在某些特殊情況下,可能會退化為 O(n)。因此,在選擇搜尋演演算法時,需要根據具體的資料分佈情況和效能需求進行考慮。
插值查詢演演算法的範例程式碼:
public class InterpolationSearch {
/**
* 插值查詢演演算法
*
* @param arr 有序陣列
* @param target 目標元素
* @return 目標元素在陣列中的索引位置,如果不存在則返回 -1
*/
public static int interpolationSearch(int[] arr, int target) {
int left = 0; // 左指標,初始為陣列起始位置
int right = arr.length - 1; // 右指標,初始為陣列結束位置
while (left <= right && target >= arr[left] && target <= arr[right]) {
// 使用插值公式估算目標元素的位置
int pos = left + ((target - arr[left]) * (right - left)) / (arr[right] - arr[left]);
if (arr[pos] == target) {
return pos; // 找到目標元素
}
if (arr[pos] < target) {
left = pos + 1; // 目標元素在右半部分
} else {
right = pos - 1; // 目標元素在左半部分
}
}
return -1; // 目標元素不存在於陣列中
}
public static void main(String[] args) {
int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = interpolationSearch(arr, target);
if (result == -1) {
System.out.println("目標元素不存在於陣列中");
} else {
System.out.println("目標元素的索引位置為: " + result);
}
}
}
斐波那契查詢
斐波那契查詢是一種基於黃金分割原理的查詢演演算法,它是對二分查詢的一種改進。斐波那契查詢利用了斐波那契數列的特性來確定查詢範圍的分割點,從而提高了查詢效率。
隨著斐波那契數列的遞增,前後兩個數的比值會越來越接近0.618,利用這個特性,我們就可以將黃金比例運用到查詢技術中,斐波那契查詢原理與前兩種相似,僅僅改變了中間結點(mid)的位置,mid不再是中間或插值得到,而是位於黃金分割點附近,即mid=low+F(k-1)-1(F代表斐波那契數列)
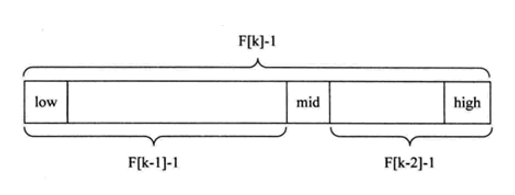
斐波那契查詢的基本思想如下:
-
首先,需要準備一個斐波那契數列,該數列滿足
每個元素等於前兩個元素之和。例如:0, 1, 1, 2, 3, 5, 8, 13, ... -
初始化左指標
left和右指標right分別指向陣列的起始位置和結束位置。 -
根據陣列長度確定一個合適的斐波那契數列元素作為分割點
mid,使得mid儘可能接近陣列長度。 -
比較目標元素與分割點mid
對應位置的元素值:
- 如果目標元素等於
arr[mid],則找到目標元素,返回位置mid。 - 如果目標元素小於
arr[mid],則說明目標元素在當前位置的左側,更新右指標為mid - 1。 - 如果目標元素大於
arr[mid],則說明目標元素在當前位置的右側,更新左指標為mid + 1。
- 如果目標元素等於
-
重複步驟 3 和步驟 4,直到找到目標元素或搜尋範圍縮小到無法繼續搜尋為止。、
斐波那契查詢的優勢在於它能夠更快地確定分割點,從而減少了比較次數。它的時間複雜度為 O(log n),與二分查詢相同。然而,斐波那契查詢需要預先計算斐波那契數列,並且在每次查詢時都需要重新確定分割點,因此在實際應用中可能會帶來一定的額外開銷。
需要注意的是,斐波那契查詢適用於有序陣列,並且陣列長度較大時效果更好。對於小規模的陣列或者無序陣列,二分查詢可能更適合。
程式碼範例:
public class FibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int [] arr = {1,4, 10, 69, 1345, 6785};
System.out.println("index=" + fibSearch(arr, 1345));// 0
}
// 生成 斐波那契數列
public static int[] fib() {
int[] f = new int[20];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
/**
*
* @param a 陣列
* @param key 我們需要查詢的關鍵碼(值)
* @return 返回對應的下標,如果沒有-1
*/
public static int fibSearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
int k = 0; //表示斐波那契分割數值的下標
int mid = 0; //存放mid值
int f[] = fib(); //獲取到斐波那契數列
//獲取到斐波那契分割數值的下標
while(high > f[k] - 1) {
k++;
}
//因為 f[k] 值 可能大於 a 的 長度,因此我們需要使用Arrays類,構造一個新的陣列,並指向temp[]
//不足的部分會使用0填充
int[] temp = Arrays.copyOf(a, f[k]);
//實際上需求使用a陣列最後的數填充 temp
for(int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
while (low <= high) { // 只要這個條件滿足,就可以找
mid = low + f[k - 1] - 1;
if(key < temp[mid]) { //我們應該繼續向陣列的前面查詢(左邊)
high = mid - 1;
//說明
//1. 全部元素 = 前面的元素 + 後邊元素
//2. f[k] = f[k-1] + f[k-2]
//因為 前面有 f[k-1]個元素,所以可以繼續拆分 f[k-1] = f[k-2] + f[k-3]
//即 在 f[k-1] 的前面繼續查詢 k--
//即下次迴圈 mid = f[k-1-1]-1
k--;
} else if ( key > temp[mid]) { // 我們應該繼續向陣列的後面查詢(右邊)
low = mid + 1;
//1. 全部元素 = 前面的元素 + 後邊元素
//2. f[k] = f[k-1] + f[k-2]
//3. 因為後面我們有f[k-2] 所以可以繼續拆分 f[k-1] = f[k-3] + f[k-4]
//4. 即在f[k-2] 的前面進行查詢 k -=2
//5. 即下次迴圈 mid = f[k - 1 - 2] - 1
k -= 2;
} else { //找到
//需要確定,返回的是哪個下標
if(mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
}
雜湊查詢
雜湊查詢演演算法(Hashing)是一種用於高效查詢資料的演演算法,它將資料儲存在雜湊表(Hash Table)中,並利用雜湊函數將資料的關鍵字對映到表中的位置。雜湊查詢的核心思想是通過雜湊函數將關鍵字轉換為表中的索引,從而實現快速的查詢操作。
在平均情況下,雜湊查詢的時間複雜度可以達到O(1)。但是,在最壞情況下,雜湊查詢的時間複雜度可能會退化到O(n),其中n是雜湊表中儲存的鍵值對數量
Java提供了用於實現雜湊表(雜湊表)的資料結構,這就是HashMap類。HashMap是Java標準庫中最常用的雜湊表實現之一,用於儲存鍵值對,並提供了快速的查詢、插入和刪除操作。
通過leetcode第一題兩數之和可以瞭解雜湊表的使用
程式碼範例
public static int[] twoSum(int[] nums, int target) {
int[] indexs = new int[2];
HashMap<Integer, Integer> hashMap = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
if (hashMap.containsKey(nums[i])){
indexs[0] = i;
indexs[1] = hashMap.get(nums[i]);
return indexs;
}
hashMap.put(target - nums[i],i);
}
return indexs;
}
二元樹查詢
二元搜尋樹是一種特殊的二元樹,它是一種有序的樹結構,可以用於實現二元樹查詢。在二元搜尋樹中,對於每個節點,其左子樹的值都小於該節點的值,而右子樹的值都大於該節點的值。這種結構使得在二元搜尋樹中可以快速地進行查詢操作。
詳細看這篇文章 二元搜尋樹