二元搜尋樹（Binary Search Tree，BST）

二元搜尋樹（Binary Search Tree），也稱二叉查詢樹或二叉排序樹，是一種特殊的二元樹，它滿足以下性質

對於二元搜尋樹的每個節點
- 左子樹中的所有節點的值都小於該節點的值
- 右子樹中的所有節點的值都大於（或等於）該節點的值
對於二元搜尋樹的任意節點，其左子樹和右子樹也是二元搜尋樹。

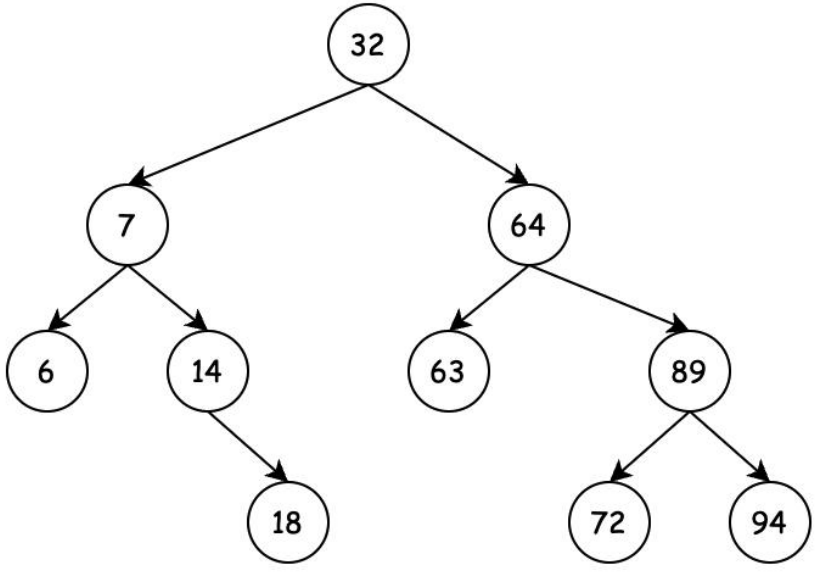
由於這種特性，二元搜尋樹可以支援高效地進行查詢、插入和刪除操作。對於查詢操作，可以通過比較目標值與當前節點的值來決定向左子樹還是右子樹進行搜尋。對於插入操作，可以按照比較結果找到合適的位置並插入新節點。對於刪除操作，則需要按照一定規則來處理不同情況下的節點刪除

插入節點

在二元搜尋樹中插入一個新節點的步驟如下：

如果樹為空，將新節點作為根節點。
如果樹不為空，從根節點開始遍歷樹。
比較要插入的值與當前節點的值。
- 如果要插入的值小於當前節點的值，向左子樹方向繼續遍歷。
- 如果要插入的值大於當前節點的值，向右子樹方向繼續遍歷。
- 如果要插入的值等於當前節點的值，根據具體需求決定是替換當前節點的值還是忽略該值。
當遇到空節點時，表示找到了合適的位置插入新節點。
建立一個新節點，並將其插入到空節點的位置。
完成插入操作。

範例程式碼：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}


class BinarySearchTree {
    private TreeNode root;

    public BinarySearchTree() {
        root = null;
    }

    // 插入節點
    public void insert(int val) {
        root = insertNode(root, val);
    }

    private TreeNode insertNode(TreeNode root, int val) {
        // 如果當前節點為空，說明找到了應該插入的位置，建立新節點並返回
        if (root == null) {
            return new TreeNode(val);
        }

        // 如果插入的值小於當前節點的值，向左子樹插入
        if (val < root.val) {
            root.left = insertNode(root.left, val);
        } else if (val > root.val) {
            // 如果插入的值大於當前節點的值，向右子樹插入
            root.right = insertNode(root.right, val);
        }

        return root;
    }
}

搜尋節點（查詢）

在二元搜尋樹中搜尋一個特定值的步驟如下：

從根節點開始，將要搜尋的值與當前節點的值進行比較。
如果要搜尋的值等於當前節點的值，返回true，表示找到了目標值。
如果要搜尋的值小於當前節點的值，則向左子樹方向繼續搜尋。
如果要搜尋的值大於當前節點的值，則向右子樹方向繼續搜尋。
如果遇到空節點，則表示未找到目標值，返回false。
重複步驟2至步驟5，直到找到目標值或搜尋完整個樹。
下面是使用上述步驟實現搜尋方法的範例程式碼：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

class BinarySearchTree {
    // 搜尋節點
    public boolean search(int val) {
        return searchNode(root, val);
    }

    private boolean searchNode(TreeNode root, int val) {
        // 當前節點為空，未找到目標值
        if (root == null) {
            return false;
        }

        // 目標值與當前節點的值相等，找到目標值
        if (val == root.val) {
            return true;
        } else if (val < root.val) {
            // 目標值小於當前節點的值，在左子樹中繼續搜尋
            return searchNode(root.left, val);
        } else {
            // 目標值大於當前節點的值，在右子樹中繼續搜尋
            return searchNode(root.right, val);
        }
    }
}

刪除節點

在二元搜尋樹中刪除一個節點的步驟如下：

從根節點開始，找到要刪除的節點。
如果要刪除的值等於當前節點的值，根據下面不同的情況進行處理：
a. 若該節點為葉節點（沒有子節點），直接刪除該節點。
b. 若該節點只有一個子節點，將其子節點替代該節點的位置。
c. 若該節點有兩個子節點，找到右子樹中最小的節點（或左子樹中最大的節點），將該節點的值替代要刪除的節點的值，然後遞迴刪除該最小節點（或最大節點）。
如果要刪除的值小於當前節點的值，則向左子樹方向繼續搜尋。
如果要刪除的值大於當前節點的值，則向右子樹方向繼續搜尋。
當遇到空節點時，表示未找到要刪除的節點。
完成刪除操作。
下面是使用上述步驟實現刪除方法的範例程式碼：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

class BinarySearchTree {
    private TreeNode deleteNode(TreeNode root, int val) {
        // 當前節點為空，未找到要刪除的節點
        if (root == null) {
            return null;
        }

        // 如果要刪除的值小於當前節點的值，在左子樹中繼續搜尋
        if (val < root.val) {
            root.left = deleteNode(root.left, val);
        } else if (val > root.val) {
            // 如果要刪除的值大於當前節點的值，在右子樹中繼續搜尋
            root.right = deleteNode(root.right, val);
        } else {
            // 找到要刪除的節點
            // 情況1: 當節點沒有子節點時，直接返回 null
            if (root.left == null && root.right == null) {
                return null;
            }
            // 情況2: 當節點只有一個子節點時，返回子節點作為當前節點的替代
            if (root.left == null) {
                return root.right;
            } else if (root.right == null) {
                return root.left;
            }
            // 情況3: 當節點有兩個子節點時，找到右子樹中最小的節點，
            //       用該節點的值替代當前節點的值，並刪除右子樹中最小的節點
            TreeNode successor = findMin(root.right);
            root.val = successor.val;
            root.right = deleteNode(root.right, successor.val);
        }

        return root;
    }

    private TreeNode findMin(TreeNode node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }
}