常見問題

閆式DP分析法

• 狀態表示
  • 集合
    • 滿足一定條件的所有方案
  • 屬性
    • 集合（所有方案）的某種屬性（Max、Min、Count等）
• 狀態計算（集合劃分）
  • 如何將當前集合劃分成多個子集合

狀態計算相當於集合的劃分：把當前集合劃分成若干個子集，使得每個子集的狀態可以先算出來，從而推導當前集合狀態（曲線救國）

集合劃分規則：不重，不漏

特殊情況：屬性是 MAX、MIN 的時候，劃分的集合是可以重複的

舉個例子 A、B、C，先求A、B的最大值，然後求B、C的最大值，最後求兩個最大值的最大值，依舊是A、B、C的最大值。例題 ⭐ 897 最長公共子序列

時間複雜度

狀態表示數量 * 狀態計算量（轉移計算量）

如完全揹包問題，假定 N 件物品，物品最低體積為 1，揹包最大體積容量 V

樸素二維情況：狀態表示數量就是 \(NV\)，狀態計算量就是物品體積為 1 的時候（最壞情況），最內層迴圈最多需計算 V 次，時間複雜度\(O(NV^2)\)

狀態轉移路徑

DP本質是在一個拓撲圖內找最短路

每個狀態\(f(i,j)\)看作一個點，狀態的轉移看作一條邊，把狀態的值理解為最短路徑長

更新最短路的規則是根據題目來的，如完全揹包規則 \(f(i,j)=Max(f(i-1,j-k*v[i])+k*w[i])\)

DP結束最終會把從 初始狀態（起點）到 目標狀態 （終點）的 最短路徑長 更新出來（生成了一顆最短路徑樹）

那麼 DP求狀態轉移路徑 就變成了在 拓撲圖 中找 最短路徑 的問題了，沿用 最短路 輸出路徑的方法就可以找出 狀態的轉移

方案總結：迴圈 與 dfs 均可實現

1. 逆推：獲取最終狀態，根據 最短路規則 逆序往前推，直到 起始狀態 ，逐一輸出每個狀態
2. 邊轉移邊記錄：狀態轉移過程中，記錄每一條邊，再利用遞推的棧機制，後序輸出

注意的點：

• 因為需要記錄路徑，狀態轉移方程可能不好被維度優化，具體問題具體分析
• 邊轉移邊記錄一般需要開一個與狀態表示一致維度的陣列，要儲存每個狀態是從上一層哪一狀態轉移過來的；而逆推不需要一致，具體可看下題（儲存每組從前組的哪個狀態轉移過來，一維）

來看一道分組揹包題1013 機器分配，要求輸出每組選擇了哪個物品，我給的題解是第一種方案的迴圈版本

從終點狀態逆推，必定有一條邊滿足最短路規則，記錄當前邊，並減去當前組物品的體積，接著開始推前一組狀態，直到起始狀態

int j = m;
for (int i = n; i; i--) {
    for (int k = 0; k <= j; k++) {
        if (f[i][j] == f[i - 1][j - k] + w[i][k]) {
            path[i] = k;
            j -= k;
            break;
        }
    }
}

可改寫成 dfs 的版本

void dfs(int i, int j) {
    if (!i) return;
    for (int k = 0; k <= j; k++) {
        if (f[i - 1][j - k] + w[i][k] == f[i][j]) {
            path[cnt++] = k;
            dfs(i - 1, j - k);
            return;
        }
    }
}

也可用第二種方案，邊轉移邊記錄（輔助下標 cnt 就不需要了）

for (int i = 1; i <= n; i++)
    for (int j = 0; j <= m; j++) {
        for (int k = 0; k <= j; k++) {
            int temp = max(f[i][j], f[i - 1][j - k] + w[i][k]);
            if (temp == f[i - 1][j - k] + w[i][k])
                path[i][j] = max(path[i][j], k);

            f[i][j] = temp;
        }
    }

cout << f[n][m] << endl;

輸出既可以迴圈輸出（倒著輸出），也可以 dfs 逆序輸出（正著輸出）

void dfs(int i, int j) {
    if (!i) return;
    int k = path[i][j];
    dfs(i - 1, j - k);
    cout << i << " " << k << endl;
}

int j = m;
for (int i = n; i >= 1; i--) {
    cout << i << " " << path[i][j] << endl;
    j -= path[i][j];
}

揹包問題初始化

變數宣告

一定要根據狀態表示的含義，來宣告所需變數

如分組揹包題 1013 機器分配，最多 10 組，每組 15 個物品，那麼定義的常數 N、M 分別表示狀態中每維的最大數量（多申請一點）

path 陣列用於邊轉移邊記錄路徑，理所應當和 f 陣列是一致維度的大小；寫成 path[N][N] 一直找不出問題的屑。

01揹包、完全揹包有相似之處

#include <algorithm>
#include <iostream>

using namespace std;

const int N = 1e3 + 10;

int n, m;
int v[N], w[N];
int f[N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = v[i]; j <= m; j++) { // 區別只在這
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }

    cout << f[m] << endl;
    return 0;
}

優化重點

01揹包和完全揹包一維優化的不同點在狀態轉移方程上

• 如果用上一層狀態就要從大到小列舉體積（01揹包二維轉一維）
• 如果用本層狀態就要從小到大列舉體積（完全揹包二維轉一維）

多重揹包

\(N\) 個物品，\(V_i\) 表示體積，\(W_i\) 表示價值，每件物品\(X_i\)個。求揹包裝得下的情況下的物品最大價值多少

• 狀態表示 \(f(i,j)\)
  • 集合
    • 只考慮前 \(i\) 個物品，且總體積不大於 \(j\) 的所有選法
  • 屬性
    • \(max\) （每個選法的總價值的最大值）
• 狀態計算
  • 轉移方程 \(f(i,j) = max(f(i-1,j-v[i] * k)+w[i]*k),k\in[0,X_i]\)，滿足 \(k*v[i]<=j\)

樸素、二維

4. 多重揹包問題 I - AcWing題庫

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e2 + 10;

int n, m;
int v[N], w[N], x[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> x[i];

    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k <= x[i] && k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    cout << f[n][m];
    return 0;
}

優化、一維⭐

二進位制法，將 \(X_i\) 拆分成 \(\lceil log_2X_i \rceil\) 個物品（\(1,2,4,8,16,...,2^k,C\)），將多重揹包轉變成01揹包問題

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1000 * 11 + 10;
int n, m;
int v[N], w[N];
int f[N];

int main() {
    cin >> n >> m;

    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        int a, b, x;
        cin >> a >> b >> x;
        int k = 1;
        while (k <= x) {
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            x -= k;
            k *= 2;
        }
        if (x > 0) {  // 若 x 還有剩餘
            cnt++;
            v[cnt] = a * x;
            w[cnt] = b * x;
        }
    }
    n = cnt;

    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--) f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

究極、單調佇列⭐

分析問題

6. 多重揹包問題 III - AcWing題庫

\(\begin{array}{l} 0<N \leq 1000 \\ 0<V \leq 20000 \\ 0<v_{i}, w_{i}, s_{i} \leq 20000 \end{array}\)

這種情況下，採用轉01揹包法，時間複雜度是 \(1000 * log_220000*20000\) = 1.4e4 + 2e4 = 3e8，肯定會TLE

單調佇列

先認識一下單調佇列是什麼 C++演演算法之旅、05 基礎篇 | 第二章 資料結構 - 小能日記

https://leetcode.cn/problems/sliding-window-maximum

#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>

using namespace std;

class Solution {
   public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> res;
        int q[nums.size()];
        memset(q, 0, sizeof q);
        int hh = 0, tt = -1;
        for (int i = 0; i < nums.size(); i++) {
            while (hh <= tt && q[hh] < i - k + 1) hh++;
            while (hh <= tt && nums[q[tt]] <= nums[i]) tt--;
            q[++tt] = i;  // 插入位置
            if (i + 1 >= k) res.push_back(nums[q[hh]]);
        }

        return res;
    }
};

解決問題

先來看多重揹包的樸素二維程式碼

for (int i = 1; i <= n; i++)
    for (int j = 0; j <= vt; j++)
        for (int k = 0; k <= s[i] && k * v[i] <= j; k++) {
            f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
        }

可以這樣優化，遍歷每個物品，然後總體積 \(j\) 分為 \(r\) 類 （\(r = v[i] - 1\)）。選擇其中一類，如第 \(r\) 類，那麼從 \(r\) 遍歷到 \(vt\) 的過程，即 int j = r; j <= vt; j += v[i] 這一過程，由於物品數量是有限的，相當於維護了一個固定寬度的滑動視窗，\(j\) 每移動一次，對滑動視窗做出滑動、刪除、插入、選擇四個操作，滑動視窗用單調佇列實現，每個物體只需遍歷一遍\([0,vt]\)，原先的 \(k\) 迴圈被優化掉了，時間複雜度變為 \(O(NV)\)

• 求 \(w[i]\) 個數，即隊內元素 \(j'\) 與當前 \(j\) 的差值 除以 \(v[i]\)；也意味著選擇了幾個 \(i\) 物品
• 滑動：隊頭元素是否出界；也就是 \(w[i]\) 的個數 > \(s[i]\) ，選擇了大於 \(s[i]\) 個物品
• 刪除：維持單調佇列特性；判斷隊尾每個 \(j'\) 對應的屬性值是否 <= \(j\) 當前對應的屬性值，True就刪除
  • 對應的值計算公式 f[i - 1][q[tt]] + (j - q[tt]) / v[i] * w[i]
• 插入：將當前 \(j\) 插入隊尾
• 選擇：從隊頭取出 \(j'\) ，對應的屬性值就是 \(f(i,j)\) 的最大值（滑動視窗 \(s[i]\) 項裡面選擇最大一項）

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

int const N = 1e3 + 10, M = 2e4 + 10;

int n, vt;
int v[N], w[N], s[N];
int f[N][M];
int q[M];

int main() {
    cin.tie(0);
    cin >> n >> vt;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i++) {
        for (int r = 0; r < v[i]; r++) {
            int hh = 0, tt = -1;
            for (int j = r; j <= vt; j += v[i]) {
                // 滑動
                if (hh <= tt && (j - q[hh]) / v[i] > s[i]) hh++;
                // 刪除
                while (hh <= tt &&
                       f[i - 1][q[tt]] + (j - q[tt]) / v[i] * w[i] <=
                           f[i - 1][j])
                    tt--;
                // 插入
                q[++tt] = j;
                // 選擇
                f[i][j] = f[i - 1][q[hh]] + (j - q[hh]) / v[i] * w[i];
            }
        }
    }

    cout << f[n][vt];
    return 0;
}

優化程式碼①

迴圈已經減少了一層，但空間依舊需要\(O(NV)\)，學著01揹包優化的思路，用捲動陣列優化一下程式碼，由於滑動的方向不可變，不能修改 for 迴圈裡的 j，可以將相鄰兩層狀態儲存到 f 陣列中 f[2][M]

• (i - 1) & 1 就是上一層
• i & 1 就是當前層

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

int const N = 1e3 + 10, M = 2e4 + 10;

int n, vt;
int v[N], w[N], s[N];
int f[2][M];
int q[M];

int main() {
    cin.tie(0);
    cin >> n >> vt;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i++) {
        for (int r = 0; r < v[i]; r++) {
            int hh = 0, tt = -1;
            for (int j = r; j <= vt; j += v[i]) {
                // 滑動
                if (hh <= tt && (j - q[hh]) / v[i] > s[i]) hh++;
                // 刪除
                while (hh <= tt &&
                       f[(i - 1) & 1][q[tt]] + (j - q[tt]) / v[i] * w[i] <=
                           f[(i - 1) & 1][j])
                    tt--;
                // 插入
                q[++tt] = j;
                // 選擇
                f[i & 1][j] = f[(i - 1) & 1][q[hh]] + (j - q[hh]) / v[i] * w[i];
            }
        }
    }

    cout << f[n & 1][vt];
    return 0;
}

優化程式碼②

不用捲動陣列也可以，宣告一個跟 f[M] 同等大小的陣列 backup[M]，用於儲存上一個物品 i 的所有狀態。新一層迴圈每次都把上一層迴圈的 f 陣列拷貝到 backup 陣列中，這樣新一層 i 就可以用到上一層 i 的狀態了

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

int const N = 1e3 + 10, M = 2e4 + 10;

int n, vt;
int v[N], w[N], s[N];
int f[M], backup[M];
int q[M];

int main() {
    cin.tie(0);
    cin >> n >> vt;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i++) {
        memcpy(backup, f, sizeof f);
        for (int r = 0; r < v[i]; r++) {
            int hh = 0, tt = -1;
            for (int j = r; j <= vt; j += v[i]) {
                // 滑動
                if (hh <= tt && (j - q[hh]) / v[i] > s[i]) hh++;
                // 刪除
                while (hh <= tt &&
                       backup[q[tt]] + (j - q[tt]) / v[i] * w[i] <= backup[j])
                    tt--;
                // 插入
                q[++tt] = j;
                // 選擇
                f[j] = backup[q[hh]] + (j - q[hh]) / v[i] * w[i];
            }
        }
    }

    cout << f[vt];
    return 0;

分組揹包

\(N\) 個分組，每個分組裡有\(X\)個物品，\(V_i\) 表示體積，\(W_i\) 表示價值，每組物品裡選一個。求揹包裝得下的情況下的物品最大價值多少

• 狀態表示 \(f(i,j)\)
  • 集合
    • 只考慮前 \(i\) 組物品，且總體積不大於 \(j\) 的所有選法
  • 屬性
    • \(max\) （每個選法的總價值的最大值）
• 狀態計算
  • 不選第 i 組物品、選第 i 組第 1 個物品、選第 i 組第 2 個物品、...選第 i 組最後一個物品
  • 不選第 i 組物品：\(f(i-1,j)\)
  • 選第 i 組物品第 k 個物品：\(f(i-1,j-v[i,k])+w[i,k]\)
    • 可能是空集 \(j < V_{ik}\) ，樸素程式碼中需要做判斷
  • 轉移方程 \(f(i,j) = max(f(i-1,j),f(i-1,j-v[i,k])+w[i,k]),k\in [1,X_i]\)，滿足 \(v[i,k]<=j\)

樸素、二維

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e2 + 10;

int n, m;
int v[N][N], w[N][N], x[N];
int f[N][N];

int main() {
    cin >> n >> m;

    for (int i = 1; i <= n; i++) {
        cin >> x[i];
        // 這裡與上面狀態轉移方程不同，下標從0開始，個人喜好
        for (int j = 0; j < x[i]; j++) { 
            cin >> v[i][j] >> w[i][j];
        }
    }

    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++) {
            f[i][j] = f[i - 1][j];
            for (int k = 0; k < x[i]; k++)
                if (v[i][k] <= j)
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
        }

    cout << f[n][m];
    return 0;
}

優化、一維

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e2 + 10;

int n, m;
int v[N][N], w[N][N], x[N];
int f[N];

int main() {
    cin >> n >> m;

    for (int i = 1; i <= n; i++) {
        cin >> x[i];
        for (int j = 0; j < x[i]; j++) {
            cin >> v[i][j] >> w[i][j];
        }
    }

    for (int i = 1; i <= n; i++)
        for (int j = m; j >= 0; j--)
            for (int k = 0; k < x[i]; k++)
                if (v[i][k] <= j) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    cout << f[m];
    return 0;
}

混合揹包

物品分類

7. 混合揹包問題 - AcWing題庫

判斷當前物品是哪個類的，然後轉移的時候按照各個類的邏輯去轉移。本題中的多重揹包還可以拆分成 01 揹包，所以只需要判斷兩個類

#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>

using namespace std;

int const N = 1e3 + 10;

int n, vt;
int f[N];

struct Thing {
    int kind;
    int v, w;
};
vector<Thing> things;

int main() {
    cin >> n >> vt;
    // 分類
    for (int i = 0; i < n; i++) {
        int v, w, s;
        cin >> v >> w >> s;
        if (s < 0)
            things.push_back({-1, v, w});
        else if (s == 0)
            things.push_back({0, v, w});
        else {
            for (int k = 1; k <= s; k *= 2) {
                s -= k;
                things.push_back({-1, v * k, w * k});
            }
            if (s > 0) things.push_back({-1, v * s, w * s});
        }
    }
    for (auto thing : things) {
        if (thing.kind < 0) {
            for (int j = vt; j >= thing.v; j--) {
                f[j] = max(f[j], f[j - thing.v] + thing.w);
            }
        } else if (thing.kind == 0) {
            for (int j = thing.v; j <= vt; j++) {
                f[j] = max(f[j], f[j - thing.v] + thing.w);
            }
        }
    }
    cout << f[vt] << endl;
    return 0;
}

二維費用

體積重量

8. 二維費用的揹包問題 - AcWing題庫

涉及到了體積與重量，將原先01揹包優化後的 \(f(i)\) 變成 \(f(i,j)\)

• \(f(i)\) 總體積不超過 \(i\) 的最大價值
• \(f(i,j)\) 總體積不超過 \(i\) 且總重量不超過 \(j\) 的最大價值

時間複雜度 \(O(NVM)\)；因為要用到上一層狀態，所以是 \(i,j\) 都是從大到小列舉；讀入物品資訊和更新一層狀態可以放在一起進行

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

int const N = 110;

int n, m, v;
int f[N][N];

int main() {
    cin >> n >> v >> m;
    for (int i = 0; i < n; i++) {
        int vx, mx, wx;
        cin >> vx >> mx >> wx;
        for (int j = v; j >= vx; j--) {
            for (int k = m; k >= mx; k--) {
                f[j][k] = max(f[j][k], f[j - vx][k - mx] + wx);
            }
        }
    }
    cout << f[v][m];
    return 0;
}

方案計數⭐

樸素、二維

11. 揹包問題求方案數 - AcWing題庫

• 狀態表示 \(g(i,j)\)
  • 集合
    • 考慮前 \(i\) 件物品，總體積恰好為 \(j\)，且總價值最大的所有選法
  • 屬性
    • \(count\)
• 狀態計算
  • 選 i 的價值的是最大的
    • \(g(i,j)=g(i-1,j-v)\)
  • 不選 i 的價值是最大的
    • \(g(i,j)=g(i-1,j)\)
  • 選 i 和不選 i 的價值都是最大的
    • \(g(i,j)=g(i-1,j-v)+g(i-1,j)\)

如何判斷狀態計算的三種情況：根據已更新完的 \(f(i,j)\) 來判斷，舉個例子，如果 \(f(i,j)\) 從 \(f(i-1,j)\) 轉移過來，那可能就是（不選 i ，選 i 和不選 i ）這兩種情況，接著判斷就行

g 陣列更新完後需要遍歷最後一層與最大總價值\(f(i,j)\)相同的各項：即考慮前 i 個物品，總體積恰好為 \([0,j]\) 的最大總價值的方案數的和

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 1e3 + 10;
int v[N], w[N];
int f[N][N];
int g[N][N];
int n, vt;
int mod = 1e9 + 7;

int main() {
    cin >> n >> vt;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= vt; j++) {
            f[i][j] = f[i - 1][j];
            if (v[i] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    }

    g[0][0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= vt; j++) {
            if (f[i][j] == f[i - 1][j]) g[i][j] = (g[i][j] + g[i - 1][j]) % mod;
            if (v[i] <= j && f[i][j] == f[i - 1][j - v[i]] + w[i])
                g[i][j] = (g[i][j] + g[i - 1][j - v[i]]) % mod;
        }
    }
    int res = 0;
    for (int j = 0; j <= vt; ++j) {
        if (f[n][j] == f[n][vt]) {
            res = (res + g[n][j]) % mod;
        }
    }
    cout << res << endl;
    return 0;
}

優化、一維

可以發現 g 陣列的更新都是根據 f 陣列狀態更新的路徑來的，兩個迴圈可以放在一塊。同時可以用一維陣列優化

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 1e3 + 10;
int v[N], w[N];
int f[N];
int g[N];
int n, vt;
int mod = 1e9 + 7;

int main() {
    cin >> n >> vt;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    g[0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = vt; j >= v[i]; j--) {
            int temp = max(f[j], f[j - v[i]] + w[i]), c = 0;
            if (temp == f[j]) c = (c + g[j]) % mod;
            if (temp == f[j - v[i]] + w[i]) c = (c + g[j - v[i]]) % mod;
            f[j] = temp, g[j] = c;
        }
    }

    int res = 0;
    for (int j = 0; j <= vt; ++j) {
        if (f[j] == f[vt]) {
            res = (res + g[j]) % mod;
        }
    }
    cout << res << endl;
    return 0;
}

方案記錄

12. 揹包問題求具體方案 - AcWing題庫

所有揹包問題都可以把方案數出來，相當於求狀態轉移路徑，本題的難點在於字典序輸出

針對第一個物品選擇有三種情況，後續物品也按這個思路考慮

• 只能選，必選
• 只能不選，必不選
• 可選可不選，必選（保證題目要求的字典序）

原來的揹包DP是從 1 推到 n，從 n 逆推的時候並不能保證字典序，況且可能有多個物品選擇方式（看看方案計數問題）

所以需要倒過來從 n 推到 1，此時 \(f(1,m)\) 就是最大總價值，就可以從 1 開始逆推了

#include <bits/stdc++.h>

using namespace std;

int const N = 1e3 + 10, V = 1e3 + 10;
int n, vt;
int v[N], w[N];
int f[N][V];
int path[N], cnt;

int main() {
    cin >> n >> vt;
    for (int i = 1; i <= n; i++) {
        cin >> v[i] >> w[i];
    }
    for (int i = n; i >= 1; i--) {
        for (int j = 0; j <= vt; j++) {
            f[i][j] = f[i + 1][j];
            if (v[i] <= j) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    }
    // f[1][m] 最大值

    int j = vt;
    for (int i = 1; i <= n; i++)
        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) {
            cout << i << ' ';
            j -= v[i];
        }

    return 0;
}

練習題

278 01揹包 計數

278. 數位組合 - AcWing題庫

• 狀態表示 \(f(i,j)\)
  • 集合
    • 考慮前 \(i\) 個物品，總體積恰好等於 \(j\) 的選法集合
  • 屬性
    • \(count\)
• 狀態計算
  • 不選第 i 物品的所有方案：\(f(i-1,j)\)
  • 選擇第 i 物品的所有方案：\(f(i-1,j-V_i)\)
  • 轉移方程：\(f(i,j) = f(i-1,j) + f(i-1,j-V_i)\)

f[0] = 1 含義

f[0] = 1; 表示從前 0 個物品選出總體積為 0 的方案數為 1；一個物品都不選，此時總體積為0，這也是一種合法的方案

二維寫法，即 \(f(i,0) = 0 , i \in [0,n]\)，表示從前 \(i\) 個物品選出總體積為 0 的方案數為 1

如計算轉移的狀態 \(f(i-1,j-s*V_i)\) 中，如果恰好 \(j-s*V_i =0\)，代表恰好 \(s\) 個 \(i\) 物品能夠滿足 \(j\) 的要求，此時是一種合法的方案

題解

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e2 + 10, M = 1e4 + 10;

int n, m;
int v[N];
int f[M];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i];

    f[0] = 1;
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--) {
            f[j] = f[j] + f[j - v[i]];
        }

    cout << f[m];
    return 0;
}

423 01揹包 Max

423. 採藥 - AcWing題庫

\(f(i,j)\)考慮前 \(i\) 個草藥，採集時間不超過 \(j\) 的所有方案的最大總價值

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e2 + 10, M = 1e3 + 10;

int n, m;
int v[N], w[N];
int f[M];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= m; i++)
        for (int j = n; j >= v[i]; j--) f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[n];
    return 0;
}

426 01揹包 Max

426. 開心的金明 - AcWing題庫

\(f(i,j)\) 考慮前 \(i\) 個物品，在不超過 \(j\) 元的情況下，所有方案的價格重要度乘積和的最大值

#include <algorithm>
#include <iostream>

using namespace std;
int const N = 1e2, M = 3e4 + 10;

int n, m;
int v[N], w[N];
int f[M];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= m; i++)
        for (int j = n; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + v[i] * w[i]);

    cout << f[n];
    return 0;
}

279 完全揹包 計數

279. 自然數拆分 - AcWing題庫

• 狀態表示 \(f(i,j)\)
  • 集合
    • 只考慮前 \(i\) 個物品（每個物品若干個），且總體積恰好等於 \(j\) 的所有選法
  • 屬性
    • \(count\)
• 狀態計算
  • 不選：\(f(i-1,j)\)
  • 選第 \(i\) 個 \(k\) 件物品：\(f(i-1,j-V_i*k)\)
  • 轉移方程 \(f(i,j) = \sum f(i-1,j-V_i*k)\) 滿足 \(k*v[i]<=j\)

以下是優化後的寫法

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 4e3 + 10;

int n;
unsigned f[N];

int main() {
    cin >> n;

    // 初始化
    f[0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = i; j <= n; j++) {
            f[j] += f[j - i];
        }
    }

    cout << (f[n] - 1) % 2147483648u << endl;

    return 0;
}

587 完全揹包 Min

587. 吃蛋糕 - AcWing題庫

• 狀態表示 \(f(i,j)\)
  • 集合
    • 考慮前 \(i\) 個物品，總體積恰好等於 \(j\) 的所有方案
  • 屬性
    • \(min\) （每個方案的元素個數）
• 狀態計算
  • 不選第 i 個：\(f(i-1,j)\)
  • 選第 i 個 k 件物品：\(f(i-1,j-V_i*k) + k\)
  • 轉移方程 \(f(i,j) = min(f(i-1,j-V_i*k) + k)\)
  • \(f(0,0)\) 為 0（什麼都不選元素個數為0）；其他 \(f(i,j)\) 全部 INF（Min）；物品數量 \(\lfloor sqrt(N) \rfloor\)

樸素寫法 （優化寫法在後面）

狀態數量 \(nlog_2n\) ，狀態轉移計算 \(n\) 次（實際比n小），時間複雜度 \(O(n^2log_2n)\)，會TLE

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

int const N = 1e2, M = 1e4 + 10;

int t, n;
int f[N][M];

int main() {
    cin >> t;
    for (int id = 1; id <= t; id++) {
        cin >> n;
        int m = 1;
        while (m * m <= n) m++;
        m--;
        // 初始化狀態
        memset(f, 0x3f, sizeof f);
        f[0][0] = 0;
        for (int i = 1; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                for (int k = 0; k * (i * i) <= j; k++) {
                    f[i][j] = min(f[i][j], f[i - 1][j - k * (i * i)] + k);
                }
            }
        }
        cout << "Case #" << id << ": " << f[m][n] << endl;
    }

    return 0;
}

優化寫法

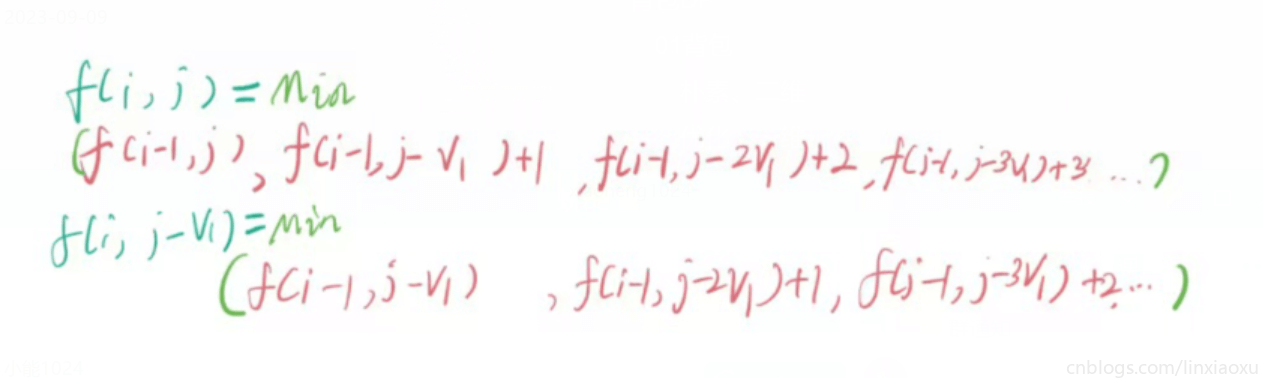
#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e3 + 10;
int n;
int a[N];
int f[N];
int g[N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) {
        f[i] = 1;  // 只有 i 一個數的情況，也就是 j = 0 情況
        g[N] = 0;
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) {
                if (f[i] < f[j] + 1) {
                    f[i] = f[j] + 1;
                    g[i] = j;
                }
            }
        }
    }
    int res = 0, last = 0;  // last 標記最長子序列末尾位置
    for (int i = 1; i <= n; i++) {
        if (f[i] > res) {
            res = f[i];
            last = i;
        }
    }
    cout << res << endl;
    cout << "路徑" << endl;
    for (int i = 1; i <= res; i++) {
        cout << a[last] << " ";
        last = g[last];
    }
    return 0;
}

896⭐最長上升子序列2

896. 最長上升子序列 II - AcWing題庫

貪心。定義一個陣列，儲存所有不同長度上升子序列結尾的最小值，隨長度增加，結尾最小值單調遞增。每次插入一個 \(a_i\) 整數二分查詢（小於某個數的最大的數），返回長度並更新陣列。時間複雜度 \(O(nlog_2n)\)。不是DP做法

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e5 + 10;
int n;
int a[N];
int q[N];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i];
    int len = 0;
    q[0] = -2e9;
    for (int i = 0; i < n; i++) {
        int l = 0, r = len;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i])
                l = mid;
            else
                r = mid - 1;
        }
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }
    cout << len;
    return 0;
}

897 最長公共子序列

897. 最長公共子序列 - AcWing題庫

• 狀態表示 \(f(i,j)\)

  • 集合
    • 在第一個序列的前 \(i\) 個字母中出現，且在第二個序列的前 \(j\) 個字母中出現的所有公共子序列
  • 屬性
    • max (每個公共子序列的長度 )

• 狀態計算

  • a[i]、b[j] 是否包含在公共子序列當中作為劃分依據（四種情況）(不出現和必須出現)

  • 00：\(f(i-1,j-1)\) （這一類情況被包含在01 | 10內）

  • 01：\(f(i-1,j)\)

    • \(f(i-1,j)\) 包含 01 的情況，求 max 是可以重複的（求數量不能重複）

  • 10：\(f(i,j-1)\)，同理

  • 11：\(f(i-1,j-1)+1\)

    • 前提是 a[i] == b[j]

一般只考慮 01、10、11 三種情況。狀態數量 \(n^2\) ，狀態轉移計算 3 次，時間複雜度 \(O(n^2)\)

因為需要從\(i-1\)層開始算，下標從1開始讀

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e3 + 10;
int n, m;
char a[N], b[N];
int f[N][N];

int main() {
    cin >> n >> m;
    scanf("%s%s", a + 1, b + 1);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

902⭐最短編輯距離

902. 最短編輯距離 - AcWing題庫

• 狀態表示 \(f(i,j)\)
  • 集合
    • 將a[1~i]變成b[1~j]的所有操作方案
  • 屬性
    • min （每個方案的操作次數）
• 狀態計算：按最後一次操作分類
  • 刪 \(f(i-1,j) + 1\)
  • 增 \(f(i,j-1) + 1\)
  • 改 \(f(i-1,j-1) + 1/0\) （看a[i]是否等於b[j]）

狀態數量 \(n^2\) ，狀態轉移計算 3 次，時間複雜度 \(O(n^2)\)

https://www.acwing.com/solution/content/5607/

相信很多人都是這麼考慮問題的：dp[i][j]為 a 的 [0..i] 轉換成 b 的 [0..j] 的最小運算元。

if (刪除的情況) dp[i][j] = dp[i-1][j] + 1;
else if (新增的情況) dp[i][j] = dp[i][j-1] + 1; 
else if (修改的情況) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i-1][j-1]; // 不需要任何操作, 和上一個狀態相同

注意，這種考慮方式不需要寫 min，因為你準確的描述了各種情況。

這樣想其實是沒有毛病的，但是難點在於你無法把 () 中的情況準確的用程式碼錶達出來。

能描述出來的只有 不需要操作 這種情況，若 a[i] == b[j] 則無需修改，其餘情況難以準確的描述。

但這題其實求的是 最短編輯距離，突出了一個最短，所以以上情況完全可以歸納為：

// 無需操作
if (a[i] == b[j]) dp[i][j] = dp[i-1][j-1];
// 新增, 刪除, 修改 都是可以到當前狀態的, 我只管取其中最小值就行
else dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1;

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

int const N = 1e3 + 10;

int n, m;
char a[N], b[N];
int f[N][N];

int main() {
    // scanf("%d%s", &n, a + 1);
    // scanf("%d%s", &m, b + 1);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    cin >> m;
    for (int i = 1; i <= m; i++) cin >> b[i];

    // 初始化 0
    // 只新增
    for (int i = 0; i <= m; i++) f[0][i] = i;
    // 只刪除
    for (int i = 0; i <= n; i++) f[i][0] = i;

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
            if (a[i] == b[j])
                f[i][j] = min(f[i][j], f[i - 1][j - 1]);
            else
                f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
        }
    }
    cout << f[n][m];
    return 0;
}

899 編輯距離

899. 編輯距離 - AcWing題庫

注意下標從 1 開始

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 15, M = 1e3 + 10;
int n, m;
int f[N][N];
char str[M][N];

int edit_distance(char a[], char b[]) {
    int la = strlen(a + 1), lb = strlen(b + 1);
    for (int i = 0; i <= lb; i++) f[0][i] = i;
    for (int i = 0; i <= la; i++) f[i][0] = i;
    for (int i = 1; i <= la; i++) {
        for (int j = 1; j <= lb; j++) {
            f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
            f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
        }
    }
    return f[la][lb];
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) cin >> (str[i] + 1);

    while (m--) {
        char s[N];
        int limit;
        cin >> (s + 1) >> limit;
        int res = 0;
        for (int i = 0; i < n; i++)
            if (edit_distance(str[i], s) <= limit) res++;

        cout << res;
    }
    return 0;
}

區間DP

282 石子合併

282. 石子合併 - AcWing題庫

• 狀態表示 \(f(i,j)\) 第 \(i\) 堆到第 \(j\) 堆的區間
  • 集合
    • 將第 i 堆石子到第 j 堆石子合併成一堆石子的所有合併方式
  • 屬性
    • \(min\) （每種合併方式的總代價 ）
• 狀態計算
  • 以最後一次合併的分界線來分類（兩堆合成一堆的分界線）
  • 左堆個數，右堆個數：1，k-1 | 2，k-2 | ... | k-1，1
  • 設分界線為k，先不考慮最後合併步驟，然後再加上最後合併的代價
  • 此時分為兩堆 \([i,k],[k+1,j]\)
  • \(f(i,j)=Min(f(i,k)+f(k+1,j)+s[j]-s[i-1])\) ，後部分是字首和求區間和
    • 左堆合併最小代價+右堆合併最小代價+最後合併的代價
    • \(k\in[i,j-1]\)

狀態數量 \(n^2\) ，狀態轉移計算 n 次，時間複雜度 \(O(n^3)\)。按區間長度從小到大列舉，從2到n

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 3e2 + 10;
int n;
int s[N];
int f[N][N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> s[i];
    for (int i = 1; i <= n; i++) s[i] += s[i - 1];

    for (int len = 2; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++) {
            int l = i, r = i + len - 1;
            f[l][r] = 1e9;  // 求min，初始化，不然每次都是 0
            for (int k = l; k < r; k++)
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
        }
    }
    cout << f[1][n];
    return 0;
}

計數DP

900⭐整數劃分

900. 整數劃分 - AcWing題庫

通用解法

• 狀態表示 \(f(i,j)\)
  • 集合
    • 考慮前 \(i\) 個物品，物品總體積恰好為 j 的所有方案。完全揹包
  • 屬性
    • \(count\)
• 狀態計算
  • 不選第 i 個：\(f(i-1,j)\)
  • 選 i 的 k 個：\(f(i-1,j-V_i*k)\)，優化為 \(f(i,j-V_i)\)
  • 轉移方程：\(f(i,j) = f(i-1,j) + f(i,j-V_i)\)

#include <algorithm>
#include <iostream>

using namespace std;

int const N = 1e3 + 10;

int n;
int v[N];
unsigned f[N];

int main() {
    cin >> n;
    f[0] = 1;
    unsigned mod = (1e9 + 7);
    for (int i = 1; i <= n; i++) {
        for (int j = i; j <= n; j++) {
            f[j] = (f[j] + f[j - i]) % mod;
        }
    }
    cout << f[n];
    return 0;
}

另類解法

• 狀態表示 \(f(i,j)\)
  • 集合
    • 總和是 \(i\) ，並且恰好表示成 \(j\) 個數的和的所有方案
  • 屬性
    • \(count\)
• 狀態計算
  • j 個數裡最小值是 1
    • \(f(i-1,j-1)\)
  • j 個數裡最小值大於 1
    • 把每一個數都減去一個1
    • \(f(i-j,j)\)
  • \(f(i,j) = f(i-1,j-1) +f(i-j,j)\)

#include <algorithm>
#include <iostream>

using namespace std;
unsigned mod = (1e9 + 7);
int const N = 1e3 + 10;
int n;
int f[N][N];

int main() {
    cin >> n;
    f[0][0] = 1;

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= i; j++) {
            f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
        }
    }
    int res = 0;
    for (int i = 1; i <= n; i++) {
        res = (res + f[n][i]) % mod;
    }
    cout << res;

    return 0;
}

狀態壓縮DP

用一個 \(n\) 位二進位制數，每一位表示一個物品，0/1 表示不同的狀態。因此可以用 \([0,2^n − 1]\) 中的所有數來列舉全部狀態

291 蒙德里安的夢想

291. 蒙德里安的夢想 - AcWing題庫、

擺放長方形的時候，先放橫著的，再放豎著的，確保能放滿。總方案數等於只放橫著小方塊的合法方案數

• 狀態表示 \(f(i,j)\)
  • 集合
    • 已將前 i -1 列擺好，且從第 i − 1 列伸出到第 i 列的狀態是 j 的所有方案
    • 狀態 j 是二進位制串，當前列每個格子的狀態如 101001（1代表前一列該行放了長方形）
  • 屬性
    • \(count\)
• 狀態計算
  • 第 i - 1 列狀態 k ，第 i 列狀態 j
  • 轉移方程 \(f(i,j) = \sum f(i-1,k)\)
  • j 與 k 需滿足
    • 沒有重行 (j & k) == 0
    • k 與 j 並集後的狀態連續 0 數量不是奇數 st[j | k]

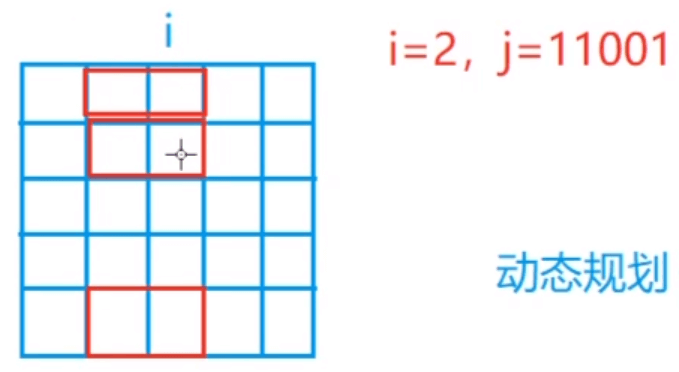
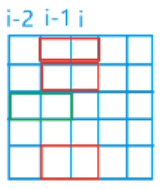
• 預處理j | k所有可能的狀態，也就是 \([1,2^n)\)，判斷每個狀態是否出現了奇數個連續0，若出現 st[i] 設定為false
• f[0][0] = 1 根據狀態表示，-1 層並不存在，橫著擺放長方形個數為 0，那麼只有豎著擺放一個方案
• f[m][0] 是最終結果，此時擺放好了 \([0,m-1]\) 層，總共 m 層，第 m 層不能橫著放長方形，因此 j 為 0

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 12, M = 1 << N;
int n, m;
long long f[N][M];
bool st[M];

int main() {
    int n, m;
    while (cin >> n >> m, n || m) {
        memset(f, 0, sizeof f);
        // 預處理，列舉所有狀態,連續0為奇數的狀態置為True
        for (int i = 0; i < (1 << n); i++) {
            st[i] = true;
            int cnt = 0;
            for (int j = 0; j < n; j++) {
                if (i >> j & 1) {
                    if (cnt & 1) {
                        st[i] = false;
                        break;
                    }
                    cnt = 0;
                } else
                    cnt++;
            }
            if (cnt & 1) st[i] = false;
        }
        // DP
        f[0][0] = 1;
        for (int i = 1; i <= m; i++) {
            for (int j = 0; j < 1 << n; j++) {
                for (int k = 0; k < 1 << n; k++) {
                    if ((j & k) == 0 && st[j | k]) f[i][j] += f[i - 1][k];
                }
            }
        }
        cout << f[m][0] << endl;
    }
    return 0;
}

91 最短Hamilton路徑

91. 最短Hamilton路徑 - AcWing題庫

樸素做法時間複雜度 \(O(n!*n)\)：最壞情況下全排列，然後每個排列算一遍長度，肯定TLE

• 狀態表示 \(f(i,j)\)
  • 集合
    • 所有從 \(0\) 點走到 \(j\) 點，走過的所有點是 \(i\) 的所有路徑
    • \(i\) 是二進位制數，每一位表示當前點是不是走過
  • 屬性
    • \(min\) （每個路徑的長度）
• 狀態計算
  • 列舉倒數第二個點是哪個點 \(k\in[0,n-1]\)
  • \(f(i-\{ j \},k)\) 所有從 0 走到 k 且不經過 j 的點的所有路徑的最短距離
  • 轉移方程 \(f(i,j) = min(f(i-\{ j \},k) + a(k,j))\)

• 從 0 開始走，0 點在二進位制1號位，所以 f[1][0] = 0

#include <bits/stdc++.h>

using namespace std;

const int N = 20, M = 1 << 20;

int n;
int w[N][N];
int f[M][N];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) cin >> w[i][j];
    }
	// 求min，初始化
    memset(f, 0x3f, sizeof f);
    f[1][0] = 0;
    for (int i = 0; i < 1 << n; i++) {
        for (int j = 0; j < n; j++) {
            // i 是否記錄已走過 j 點
            if (i >> j & 1)
                for (int k = 0; k < n; k++) {
                    // i 記錄了 k 點
                    if (i >> k & 1)
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
                }
        }
    }

    cout << f[(1 << n) - 1][n - 1] << endl;

    return 0;
}

樹形DP⭐

285 沒有上司的舞會

AcWing 285. 沒有上司的舞會 - AcWing

• 狀態表示 \(f(u,0)\) \(f(u,1)\)
  • 集合
    • \(f(u,0)\) 以 u 為根的子樹中選擇，並且不選 u 這個點的所有方案
    • \(f(u,1)\) 以 u 為根的子樹中選擇，並且選 u 這個點的所有方案
  • 屬性
    • \(max\) （每個方案的快樂指數）
• 狀態計算 （\(si\) 為 u 的所有兒子）
  • \(f(u,0) = \sum Max(f(si,0),f(si,1))\)
  • \(f(u,1) = \sum f(si,0)\)

所有節點總兒子數量等於邊數 n - 1 ，整個問題時間複雜度 \(O(n)\)

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

int const N = 6e3 + 10;

int n;
int happy[N];
int h[N], e[N], ne[N], idx;
int f[N][2];
bool has_father[N];

void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void dfs(int u) {
    f[u][1] = happy[u];

    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        dfs(j);
        f[u][0] += max(f[j][0], f[j][1]);
        f[u][1] += f[j][0];
    }
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> happy[i];
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b;
        has_father[a] = true;
        add(b, a);
    }
    int root = 1;
    while (has_father[root]) root++;

    dfs(root);

    cout << (max(f[root][0], f[root][1])) << endl;
    return 0;
}

記憶化搜尋

每一道動態規劃問題都可以用遞迴方式來寫（如上面的樹形DP）

901 滑雪

901. 滑雪 - AcWing題庫

• 狀態表示 \(f(i,j)\)
  • 集合
    • 從 \(i,j\) 開始滑的所有路徑
  • 屬性
    • \(max\) （每個路徑的長度）
• 狀態計算
  • 按第一步往哪個方向滑分為四類（即先不考慮第一步，再考慮第一步）
  • 往右劃： \(f(i,j+1) + 1\) ，其他同理（要考慮存在條件，滑到點高度小於當前點）

同時遞迴不應該存在環。題目能滿足要求（點與點的高度差關係）

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

int const N = 3e2 + 10;

int n, m;
int h[N][N];
int f[N][N];

int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};

int dp(int x, int y) {
    int &v = f[x][y];
    if (v != -1) return v;
    v = 1;  // 不能走，路徑為1
    for (int i = 0; i < 4; i++) {
        int nx = x + dx[i], ny = y + dy[i];
        if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && h[nx][ny] < h[x][y]) {
            v = max(v, dp(nx, ny) + 1);
        }
    }
    return v;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) cin >> h[i][j];

    memset(f, -1, sizeof f);
    int res = 0;
    // 遍歷每一個起點的最大值
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) res = max(res, dp(i, j));
    cout << res;
    return 0;
}

參考資料

感謝所有大佬的題解，所有部落格知識分享。ORZ

OI Wiki - OI Wiki (oi-wiki.org)

多重揹包問題 III【單調佇列優化+圖示】

AcWing 11. 揹包問題求方案數【揹包DP求最優方案總數】

揹包問題中 體積至多是 j ，恰好是 j ，至少是 j 的初始化問題的研究

AcWing 1013. 機器分配【分組揹包+揹包DP輸出方案—拓撲圖分析】 - AcWing

AcWing 291. 蒙德里安的夢想 - AcWing

AcWing 291. 蒙德里安的夢想（詳細註釋 ） - AcWing

AcWing 91. 最短Hamilton路徑(超詳解) - AcWing

AcWing 12. 揹包問題求具體方案【01揹包 + 揹包DP輸出方案】 - AcWing