本文介紹基於ArcMap軟體，實現普通克里格、迴歸克里格方法的空間插值的具體操作。

1 背景知識準備

  前期幾篇部落格分別基於地學計算的基本概念與相關操作，進行了詳細的講解：

  地統計學的基本概念及公式詳解：地學計算主要概念及公式推導全解；

  MATLAB計算變異函數並繪製經驗半方差圖：空間資料變異函數計算與經驗半方差圖繪製。

  全域性多項式（趨勢面）與IDW逆距離加權插值：MATLAB程式碼：空間資料全域性多項式插值法（趨勢面法）與逆距離加權（IDW）法插值與結果分析。

  本文所涉及相關操作的原理與對應程式碼等，都在上述三篇部落格中，本次就不再贅述。

  結合以上相關基礎知識與基本操作方法，本次我們就將通過迴歸克里格與普通克里格這兩種方法，基於ArcMap、MATLAB、SPSS等軟體，計算土壤空間屬性插值的數值。其中，由於本文所用的土壤取樣點空間資料集並不是我的，因此遺憾不能將這一資料一併提供給大家；但是依據本篇部落格的思想與對操作步驟的詳細解釋，大家用自己手頭的資料，可以將相關操作與分析過程加以完整重現。

  本文所用的軟體：AcrMap 10.2軟體、SPSS 25軟體、MATLAB R2018a軟體、Microsoft Office Excel 2019軟體。

  本文所用的資料：研究區域的向量地圖與空間資料集，其中空間資料集包括湖北省荊門市沙洋縣288個土壤取樣點位置資料與土壤有機質含量資料，以及對應區域90米解析度高程（DEM90）、長度坡度係數（Length-Slope Factor，LS）、水流強度指數（Stream Power Index，SPI）、徑流指數（the Wetness Index，WTI）等13個環境變數[1, 2]。其中，本文將上述13種環境變數分別簡寫作CH、CV、HillShade、LS、m、QFD、SOS、SPI、DEM90、WTI、α、β、Ω。

2 迴歸克里格實現

2.1 取樣點與環境變數提取

  本文中，我所使用的288個初始土壤取樣點資料為向量圖層檔案，後續對其分析時需要提取為具體列表的形式；另一方面，本文13個初始環境變數資料均為柵格圖層，呈面狀分佈；為進行後續迴歸方程求解、殘差計算等操作，我們同樣需要將各環境變數在取樣點上的數值加以提取。上述步驟均在AcrMap 10.2軟體中實現。

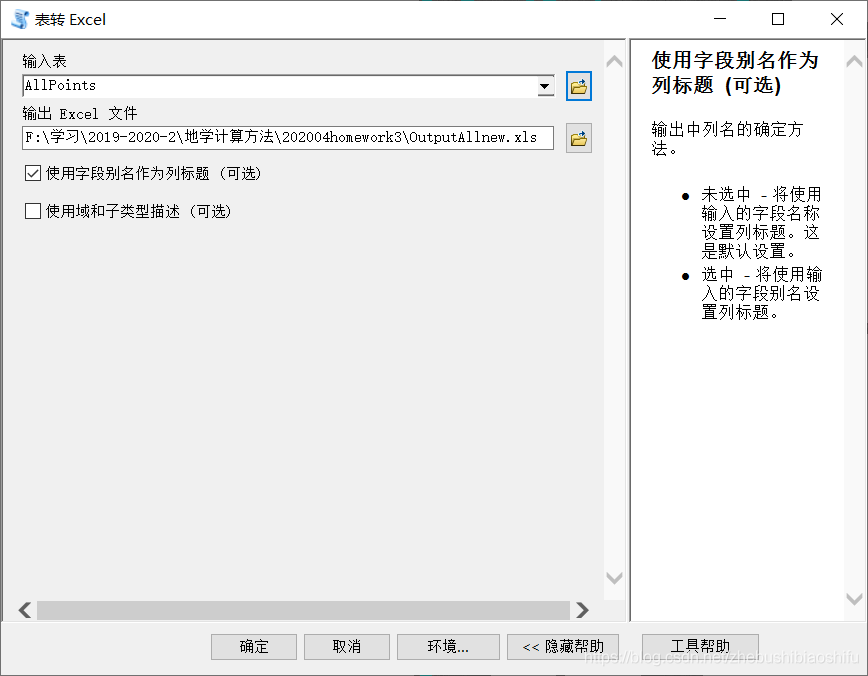
  在AcrMap軟體中，首先將取樣點向量圖層匯入，並選擇「系統工具箱」→「Conversion Tools」→「Excel」→「錶轉Excel」，設定輸入表、輸出路徑等資訊後點選「確定」。這一步驟亦可於環境變數提取後進行。

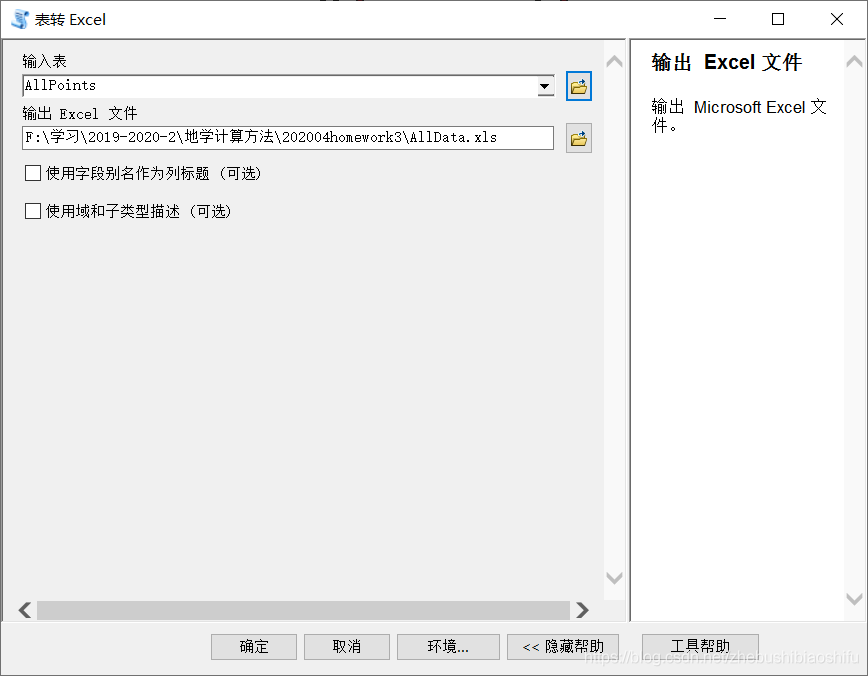
  隨後，利用「系統工具箱」→「Spatial Analyst Tools」→「提取分析」→「多值提取到點」模組，對13個環境變數分別進行取樣點對應位置的數值提取。提取時發現，若不由圖層列表選擇環境變數，而是由資源管理器直接選擇，可以進行較為方便的多選操作。

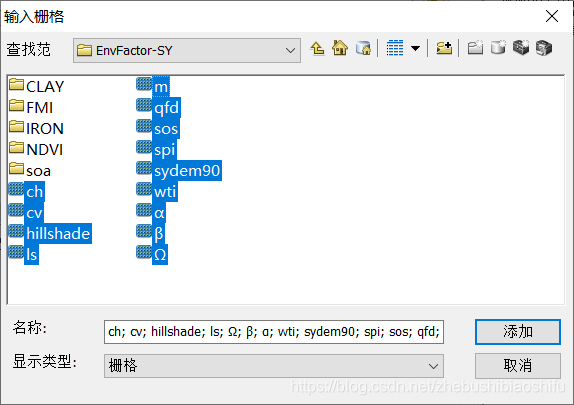
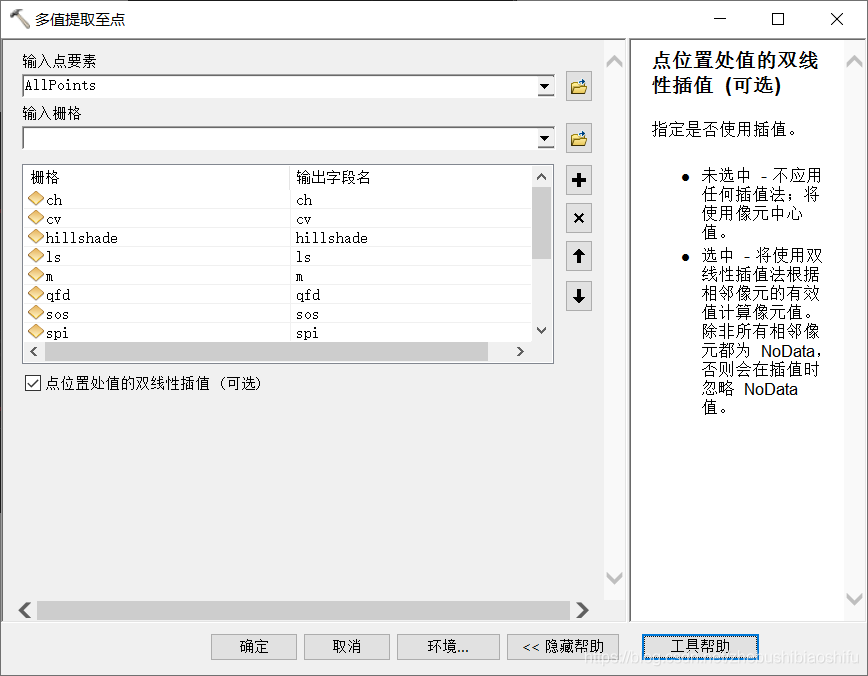
  提取完畢後，可以在取樣點圖層的屬性表中檢視288個點的位置資訊、土壤有機質含量及其各自分別對應的13個環境變數的數值。隨後發現，提取出的環境變數數值具有某個點多為0的情況。這一問題隨後通過調整操作得以解決，具體附於本文5.3部分。

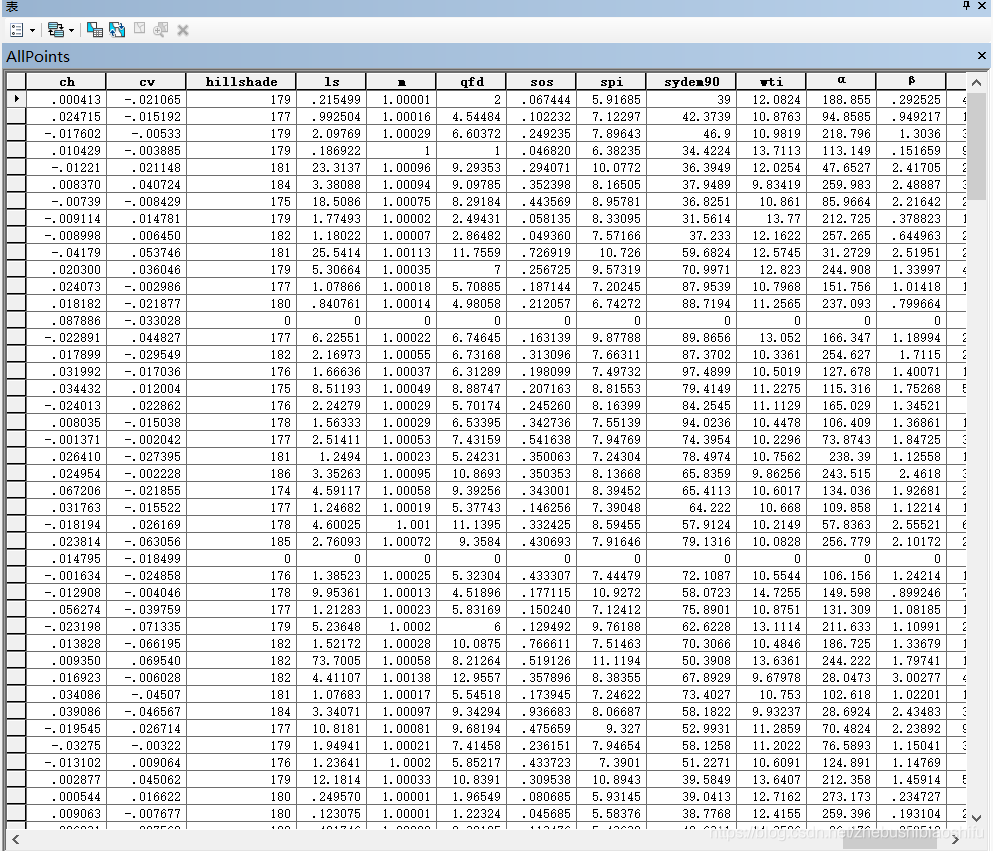
  選擇「系統工具箱」→「Conversion Tools」→「Excel」→「錶轉Excel」，設定輸入表、輸出路徑等資訊後點選「確定」，即可將包含有13個環境變數資訊的取樣點屬性表匯出。

2.2 子集要素劃分

  由於後期我們需要藉助驗證資料集對迴歸克里格與普通克里格方法進行對比，因此需要劃分子集要素。

  選擇「系統工具箱」→「Geostatistical Analyst Tools」→「工具」→「子集要素」，設定相關屬性後點選確認。

  其中，設定訓練要素為全部取樣點中隨機選取佔比80%的部分，設定測試要素為全部取樣點中隨機選取佔比20%的部分。

  可以分別用兩種不同顏色表示訓練要素對應的點與測試要素對應的點，如下所示。

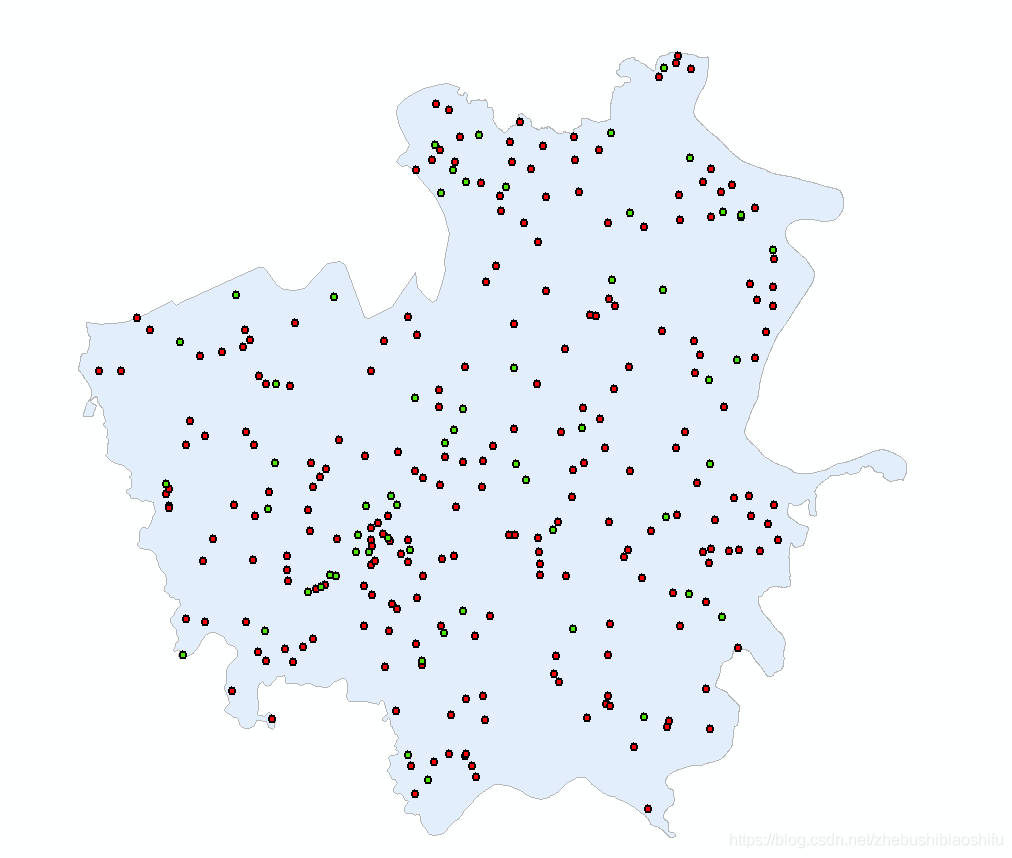
  後期將用上述訓練要素與測試要素資料對迴歸克里格與普通克里格插值結果加以對比。

2.3 異常值提取

  首先，將分佈於環境變數圖層外的一個取樣點剔除。這一部分的具體說明附於本文5.3部分。

  此外，由於288個土壤取樣點對應有機質含量資料為實測資料，其在取樣記錄、實驗室測試等過程中，可能具有一定誤差，從而出現個別異常值；而異常值的存在會對後期空間插值效果產生較大影響。因此，結合本文開頭所提及的部落格以及資料的實際情況，我們選用「平均值加標準差」方法的「3S」方式，藉助MATLAB軟體對本次作業異常資料加以篩選、剔除。

  下圖即為通過MATLAB篩選出的訓練要素中的異常值點號資訊。異常值需要在Excel與ArcMap中同時剔除。

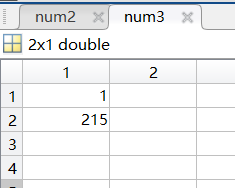
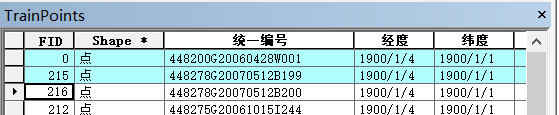
2.4 土壤有機質含量經典統計學分析

  運用SPSS軟體對剔除異常值之後的285個取樣點有機質含量資料加以統計分析。

  結果如表1所示。

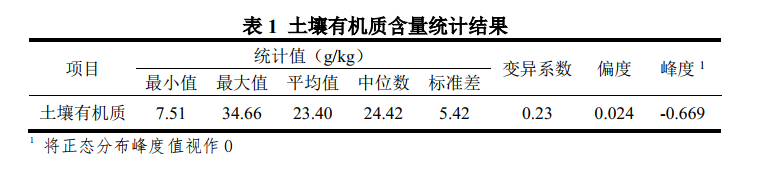
  由表1可得，上述取樣點土壤有機質含量最小值為7.51g/kg，最大值為34.66 g/kg；其平均值與中位數，相差不大，說明有機質分佈整體較為均勻；其變異係數為0.23，呈現出中等變異性。其偏度與峰度分別為0.024與-0.669，說明其分佈陡緩程度與正態分佈較為類似，但稍偏尖頂峰狀態；其斜偏度較之正態分佈具有一定差距，呈現左偏。

2.5 迴歸方程求取

  資料預處理結束後，即可開始利用訓練要素中各點有機質含量及其對應的13個環境變數數值，求取其間的迴歸方程。

  首先需要將上述資料匯入SPSS軟體。

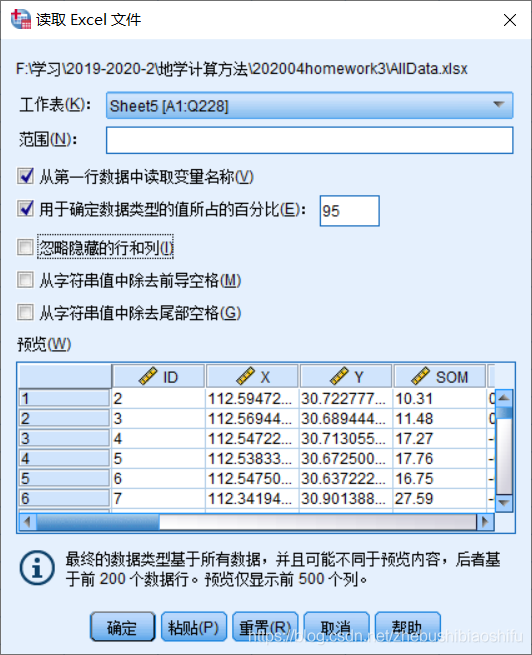
  在SPSS軟體中，選擇「分析」→「相關」→「雙變數」，利用皮爾遜相關係數在雙尾檢驗條件下，對土壤有機質含量與其它13個環境變數之間的相關性加以探究。

  相關性結果如表2所示。

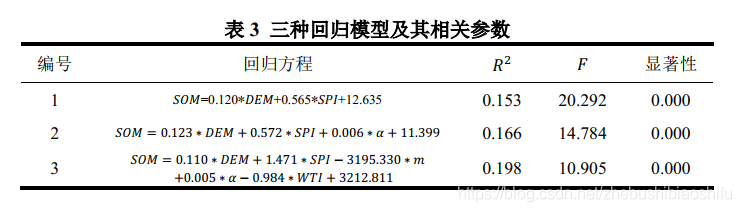
  隨後，選擇「分析」→「迴歸」→「線性」，將「方法」設定為「步進」，並分別設定進入和除去的概率為0.05、0.10，0.10、0.11與0.15、0.20。將上述三種概率對應的迴歸模型分別編號為1、2與3，並依次得到三種模型對應的迴歸方程、R^2、F與顯著性。

  對應迴歸模型及其引數如表3所示。

2.6 殘差提取

  得到上述三種迴歸模型後，分別利用已有環境變數柵格圖層對土壤有機質含量以及計算。

  在ArcMap軟體中，利用「系統工具箱」→「Spatial Analyst Tools」→「地圖代數」→「柵格計算器」模組，分別生成三種迴歸模型對應的土壤有機質含量圖層。

  求出上述三個土壤有機質含量圖層後，利用「系統工具箱」→「Spatial Analyst Tools」→「提取分析」→「多值提取到點」模組，提取出訓練要素中各點對應的有機質含量數值。

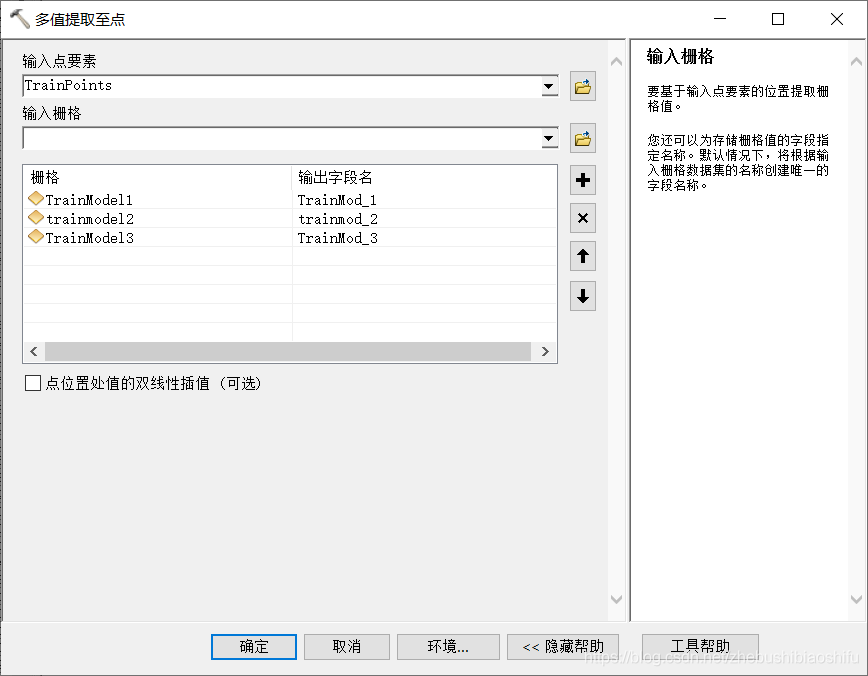
  提取後匯入到Excel軟體，並利用Excel分別求出上述三種迴歸模型對應訓練要素各點的殘差。

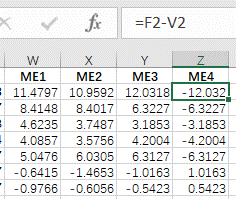
  利用MATLAB軟體對三種迴歸模型對應殘差進行正態分佈檢驗，發現模型三殘差原始資料符合正態分佈，因此此處暫選擇模型三進行後續計算。隨後發現其所得結果出現異常值，且考慮到模型三變數顯著性水平選取過高，因此最終藉助模型二對應殘差重新執行下述操作，求得最終有機質含量回歸克里格結果。

2.7 殘差普通克里格求解

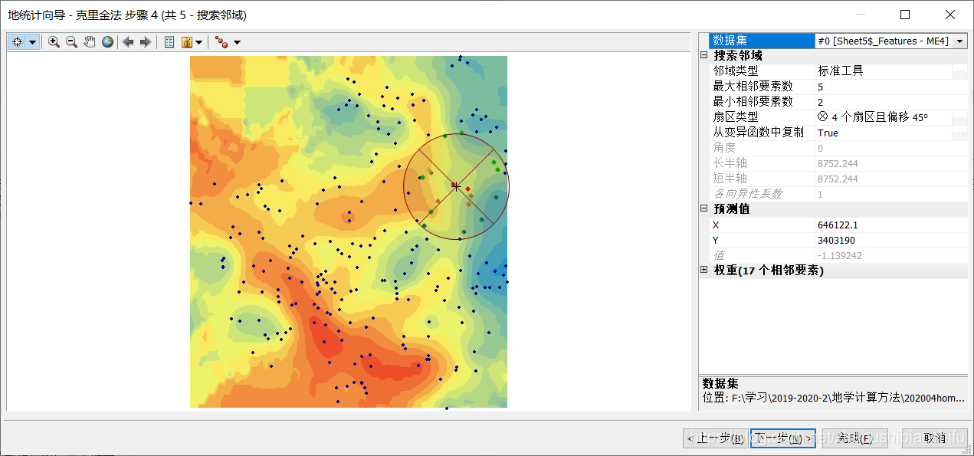
  將上述求得的訓練要素各點對應殘差資料匯入ArcMap軟體訓練要素點圖層中，利用「Geostatistical Analyst Tools」→「地統計嚮導」→「克里金法/協同克里金法」模組，對殘差加以普通克里格插值。

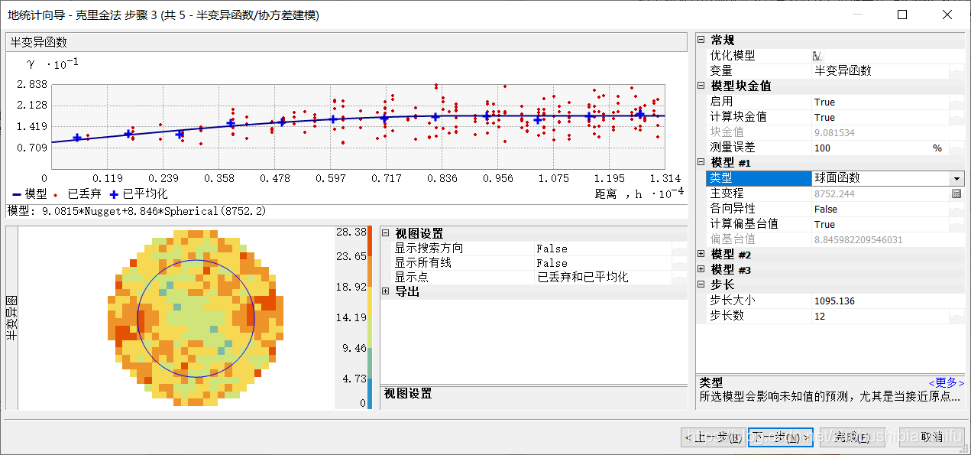
  試驗變異函數散點圖及其擬合如下。

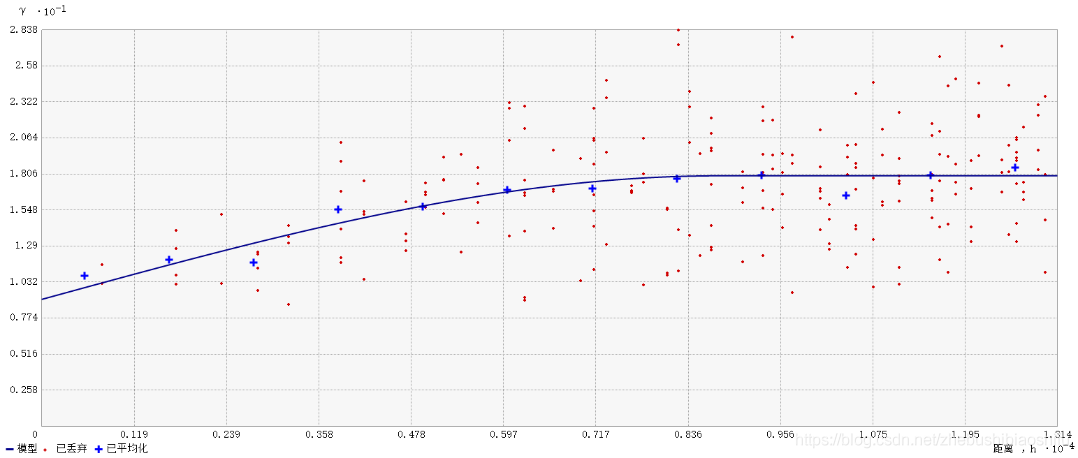
  設定相關屬性，完成普通克里格插值。其中，由於殘差資料自身已通過正態分佈檢驗，因此未在上述步驟對資料加以變換。同時，依據計算得出試驗變異函數散點圖，選擇球狀模型對其加以擬合。

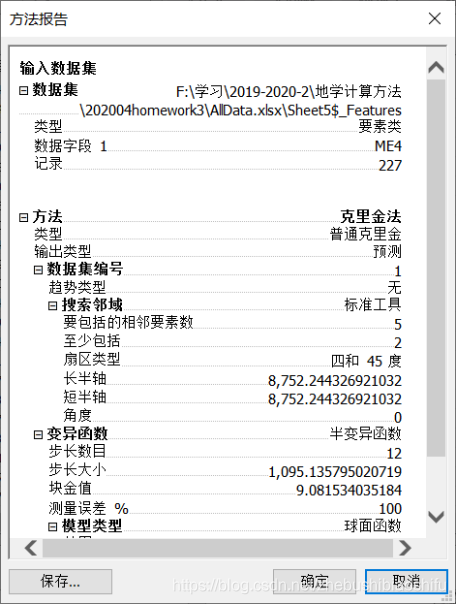
  得到結果圖層如下所示。

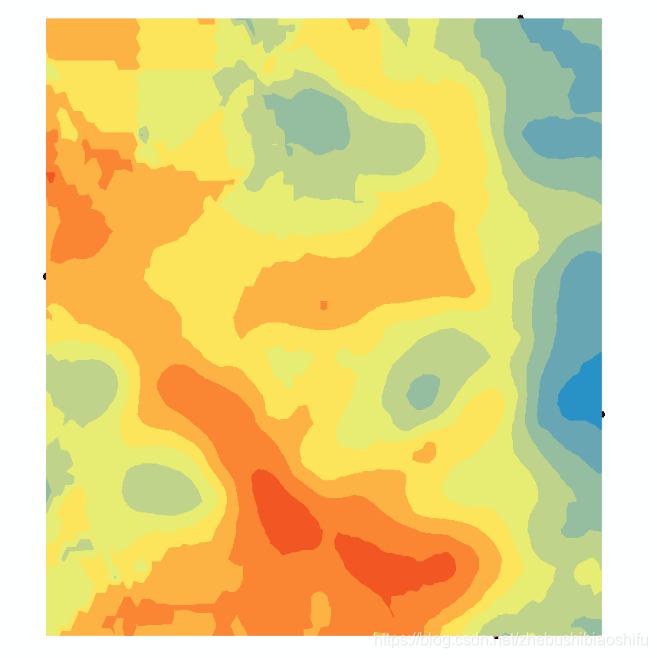
  將沙洋縣區域圖層同時疊加，可以看到普通克里格插值結果並未完全覆蓋沙洋縣整個區域。

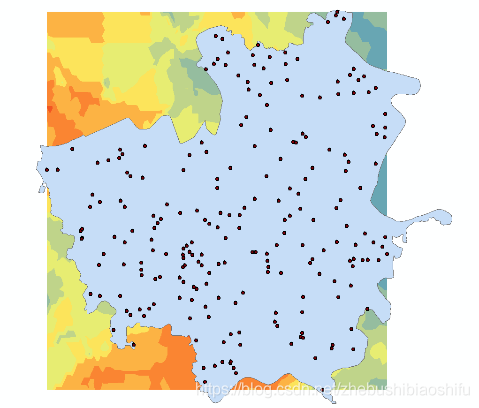
  利用結果圖層的「圖層屬性」→「範圍」模組，將插值結果擴大至完全覆蓋沙洋縣。

  確認無誤後，利用結果圖層的「資料」→「匯出資料」模組，將殘差克里格插值結果圖層轉為柵格面圖層，並依據沙洋縣邊界範圍將得到的柵格面圖層加以剪裁。

  剪裁後，即可得到沙洋縣土壤有機質含量殘差的普通克里格插值完整結果圖層。

2.8 土壤有機質含量回歸克里格求解

  在ArcMap軟體中，利用「系統工具箱」→「Spatial Analyst Tools」→「地圖代數」→「柵格計算器」模組，將上述殘差克里格插值結果圖層與前述模型三所對應迴歸方程計算結果圖層相加，從而得到利用迴歸克里格插值方法計算的沙洋縣土壤有機質含量插值結果圖層。

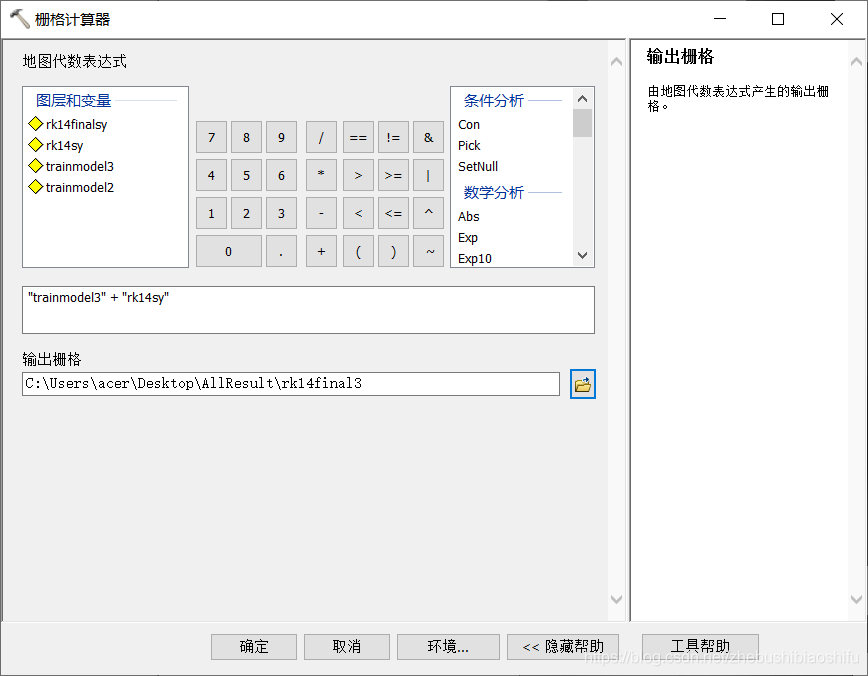
  得到結果如下所示。

  可以看到其中具有-140左右的異常值；嘗試運用前述模型二進行同樣的求解操作，發現異常值不再存在。針對這一問題的思考與結論，具體附於本文5.7部分。

2.9 迴歸克里格精度評定

  隨後，利用「系統工具箱」→「Spatial Analyst Tools」→「提取分析」→「多值提取到點」模組，將土壤有機質含量的迴歸克里格插值結果提取至測試要素對應點位置。

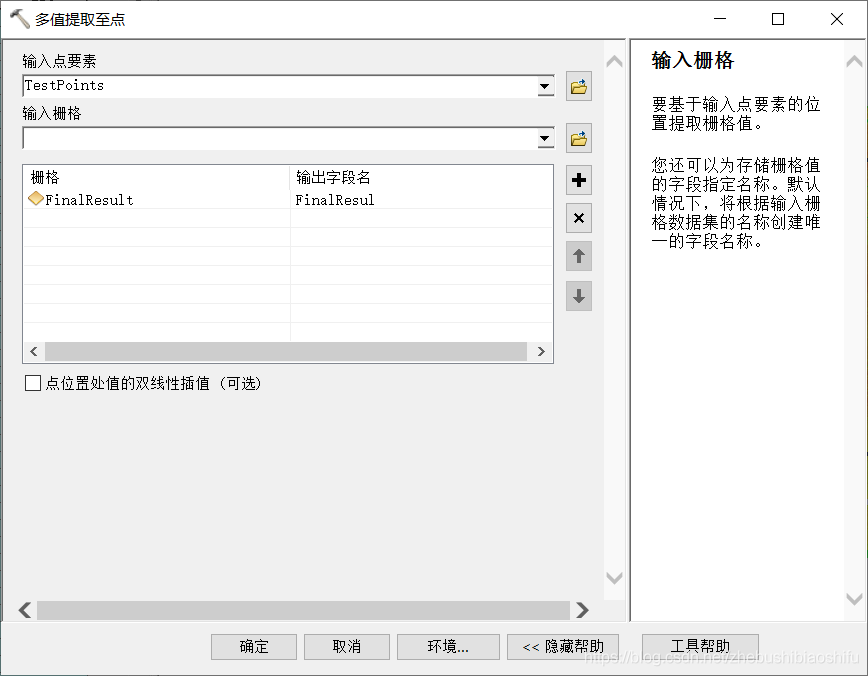
  利用MATLAB軟體，求取測試要素中各點土壤有機質含量實測值與迴歸克里格計算結果之間精度衡量指標。

  各精度衡量指標結果如表4所示。

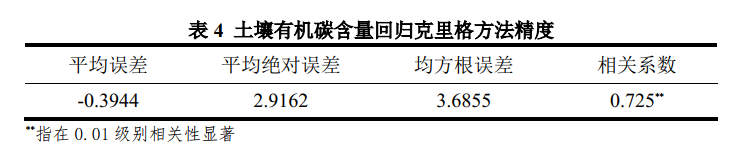
2.10 迴歸克里格專題地圖製作

  首先，將計算過程中的殘差普通克里格插值結果、迴歸方程計算結果等製作為專題地圖。其中，由於暫未找到相關精確資源，因此下列展示結果未對沙洋縣境內的水體加以區分。這一問題亦在本文5.8部分有所討論。

  最後，將基於迴歸克里格方法得出的沙洋縣土壤有機質含量插值結果製作為專題地圖。

3 普通克里格實現

  基於與前述內容類似的步驟，直接將經過異常值剔除的訓練要素各點對應的土壤有機質含量進行普通克里格插值。

  其中，由於土壤有機質含量均為正數，因此在進行克里格插值時採取了Box-Cox變換。

  試驗變異函數散點圖及其擬合如下。

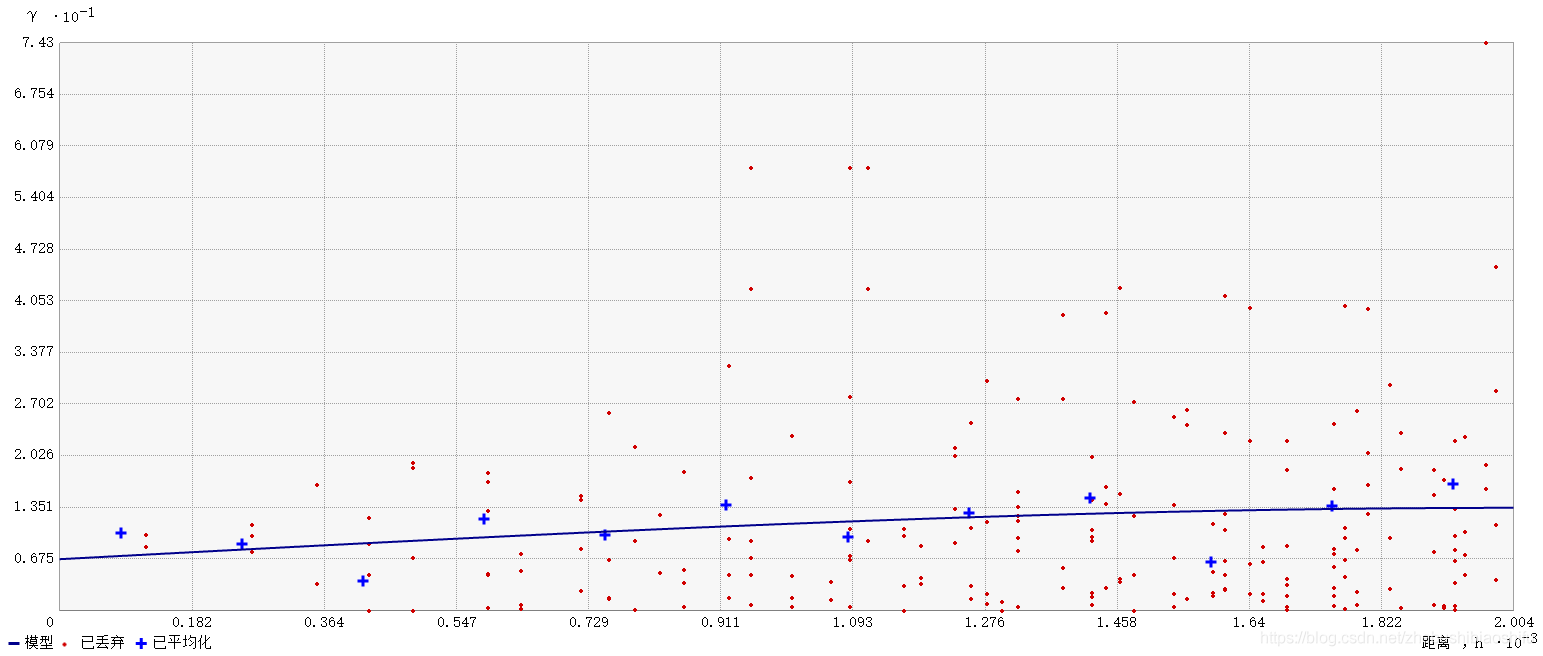
3.1 普通克里格精度評定

  利用測試要素對普通克里格插值結果加以精度衡量，所得各項精度衡量指標如表5所示。

3.2 普通克里格專題地圖製作

  將基於普通克里格方法得出的沙洋縣土壤有機質含量插值結果製作為專題地圖。

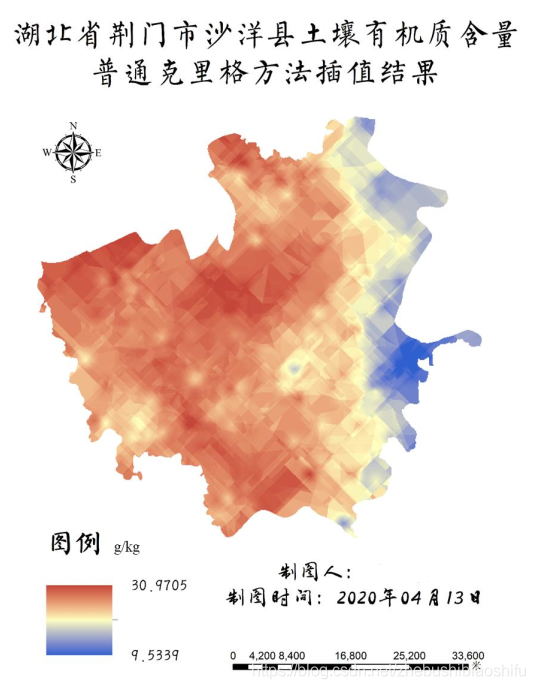
4 兩種插值方法對比

  結合上述迴歸克里格與普通克里格所得結果，由精度與實際結果等角度對兩種方法加以對比、分析。

4.1 精度對比

  將前述迴歸克里格插值與普通克里格插值結果精度衡量指標加以對比，探究兩種方法的效果。

  指標對比如表6所示。

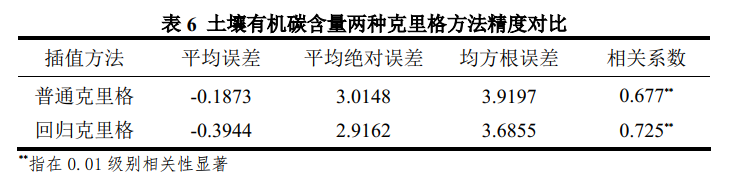
  由表6可知，由整體角度觀之，普通克里格插值方法與迴歸克里格方法對應平均誤差、平均絕對誤差與均方根誤差均較小，即二者對於土壤有機質含量的插值計算結果較為準確。

  由兩種方法結果對應精度衡量指標觀之，普通克里格方法對應平均誤差較小於迴歸克里格方法；而普通克里格方法平均絕對誤差與均方根誤差均較大於迴歸克里格方法，且其相關係數小於後者。

  其中，由於平均誤差在計算時未對誤差求得絕對值[3]，因此其符號可以反應計算結果與實測值的大小關係，其數值大小則表明所得結果的可靠程度；而平均絕對誤差和均方根誤差均可以分別較好反應出計算值與實測值之間誤差的實際情況與殘差的樣本標準差；相關係數則可以評價計算值與實測值之間的線性相關程度。

  由此可以看出，兩種克里格方法求得的土壤有機質含量資料均較大於實測資料，但二者計算結果的整體準確性較高；其中，迴歸克里格方法求得的測試要素點土壤有機質含量較之普通克里格方法，平均絕對誤差降低3.27%左右，均方根誤差降低5.97%左右。

  綜上所述，迴歸克里格方法相對普通克里格方法所得計算結果更加準確，在一定程度上提高了空間插值的效果。

4.2 插值結果對比

  藉助上述普通克里格與迴歸克里格插值方法所得結果圖，對其各自特點加以對比、分析。

  此處值得注意的是，本文前述兩幅克里格插值結果圖層中，我均採用了「拉伸」色帶式圖例。而為更好對二者插值結果圖加以對比，此處將二者結果圖層的圖例加以統一處理，運用相同的圖例表示方式，即使得兩幅圖中同一顏色代表相同的數值含義。

  對比上述兩幅圖。由空間區位分佈角度觀之，普通克里格方法與迴歸克里格方法所得插值結果整體趨勢一致，呈現出土壤有機質含量自沙洋縣中、西部地區向東部地區遞減的變化特徵。即在沙洋縣中部、西北部，包括南部地區，土壤有機質含量整體較高，而在東部地區含量整體較低；其中，含量最高區域主要分佈於沙洋縣中部夾堰村一帶與西部常家灣一帶，含量最低地區則主要分佈於沙洋縣東部新村、登家臺一帶。

  由空間聚集分佈角度觀之，普通克里格方法所得插值結果整體較為平緩，多呈現塊狀分佈，形成較類似於等高線狀的區域性極大值或極小值中心分佈趨勢；而回歸克里格方法所得插值結果較之前者更加分散、零碎，空間變異較為複雜，很少出現結果聚集分佈的態勢；很好展現出一些區域性空間、細節地區的土壤有機質含量情況。

  此外，可以看到迴歸克里格方法插值結果可以明顯呈現出沙洋縣河流的分佈區位，以及其南部地區明顯可以看到長湖的分佈位置；而在普通克里格方法插值結果中則看不出這些細節。之所以出現這樣的原因，我認為是因為迴歸克里格中起到主要決定作用的趨勢項造成的。如本文第二部分所述，在迴歸克里格方法計算過程中，由於趨勢項在通過迴歸方程求解時，融入了大量環境要素（其中就包括與河流關係較為密切的SPI），因此可以較為明顯的看出上述河流、湖泊等環境要素的區位資訊。

  此外，由於上述兩幅圖使用同一圖例，或暫時看不出普通克里格方法與迴歸克里格方法插值結果的數值範圍差異。而若結合前述兩幅專題地圖，則可以看出普通克里格的插值結果區間為9.5339至30.9705g/kg，而回歸克里格的插值結果區間為6.6434至34.0612g/kg；即迴歸克里格插值結果範圍區間較之普通克里格大。

  這一結果亦符合相關文獻的研究成果[3]。這一現象的原因為，普通克里格插值由於更多依賴於臨近點的實測值，通過變異函數等加以待插點數值的計算，因而各點所受臨近取樣點的影響較大，從而導致各點插值結果趨於平緩，從而進一步「磨滅」了資料的極值，導致最大值被過低估計，而最小值被過高估計；因此產生這一現象。

5 一些值得討論的問題

  將一些在上述操作過程中遇到的，或者我所想到的問題，在這裡統一記錄與思考。

5.1 範疇型變數求解

  本文前述各環境變數均為連續型變數，相關操作均為對具體的連續型數值資訊加以處理，屬於「硬插值」[1, 7]；這種方法在一定程度上忽視了非數值型別變數對土壤相關屬性的影響，如土壤型別、土壤質地等[7]。因此，結合考慮了資料不確定性的「軟資料」，將非數值型別變數納入計算範圍，可以較為有效地提高計算精度[7]。參考相關資料，結合數學建模相關知識，嘗試由研究方法與實際處理兩個角度針對範疇型變數展開討論。

  在研究方法層面，一是可通過變換研究方法方式對其加以處理。有學者通過貝葉斯最大熵（Bayesian Maximum Entropy，BME）方法，將相關環境屬性資料預測分為先驗階段與後驗階段兩個部分。其中，先驗階段依據經典統計學指標、自然法則等一般知識資料計算先驗概率密度函數；而在後驗階段，將「硬資料」與「軟資料」結合，進行貝葉斯條件化，獲取後驗概率密度函數，並進而完成計算[7, 8]。

  二是可對部分操作所選用方法加以調整。例如，在相關性分析層面，本文選擇對13個相關環境變數與土壤有機質含量進行皮爾遜相關性分析；而針對範疇型變數，例如對兩個無序分類變數進行相關性檢驗，則需要藉助卡方檢驗（Chi-square Test），由理論頻數和實際頻數的吻合程度對變數的相關性加以定量分析。在迴歸分析層面，本文選擇利用線性逐步迴歸對模型加以求解；而針對範疇型變數進行迴歸方程求解，如因變數為一個無序分類變數，自變數為多個無序分類變數或多個二分變數（多分類變數亦可，但二分變數運用較多）與連續變數結合，則可使用Logistic迴歸方法。

  上述討論在研究方法層面對包含範疇型變數的資料處理加以探究。而在更為具體的實際處理層面，可通過如下方式對範疇型變數加以計算。

  一是可對範疇型變數自身加以變換。可選擇直接將某一多分類變數對應各類分別轉換為若干二分變數，進而直接利用上述轉換後的二分變數加以相關處理與計算。

  其中，以不同土壤質地型別的劃分為例，探討範疇型變數變換這一方法。文獻[2]將土壤質地型別分為Light loam、Loam、Sandy loam、Sand、Fine sand與Medium loam等6類；則我們可分別使用x_1、x_2、x_3、x_4、x_5、x_6等6個二分變數對其加以表示：

  其中，6個二分變數同時僅可有一個為1，其餘均為0。

  隨後，可將回歸方程寫作：

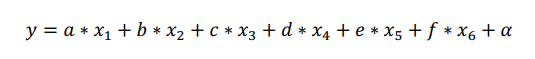
  其中，a、b、c、d、e、f均為係數，α為其它環境變數對應項。通過這一公式，即可將範疇型變數進行定量化計算。

  二是可建立範疇型變數與連續型資料變數之間的關係。文獻[7]依據土壤有機質含量將訓練集中各點分為n組，並分別對各組統計組內屬於各土壤質地類別的點數，並將各點數除以該組點數總和，作可作為有機質與土壤質地之間的定量關係。

  其中，R_(〖OM〗_k )表示第k個有機質組對於土壤質地的定量關係，〖ZD〗1表示第1個土壤質地類別，〖cou〗(1,k)表示第k個有機質組中屬於第1個土壤質地類別的點個數，〖cou〗_k表示第k個有機質組中全部點個數，m表示土壤質地類別總數。

  隨後，依據待預測點Z_ij所屬土壤質地類別，依據上式反求出該點有機質取值概率，即其對第k個有機質組的相似度。

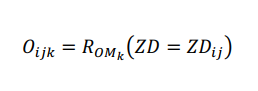
  將該點對各有機質組的相似度歸一化，則可獲得該點對應有機質含量的模糊分佈。至此，即將上述土壤質地這一範疇型變數轉換為具有一定不確定性的「軟資料」，並進一步進行後續計算。

5.2 ArcMap崩潰

  本文操作部分初期，若直接將原始288個土壤取樣點匯入個人電腦ArcMap 10.2軟體中，會出現軟體強制停止執行的現象；多次嘗試無果。多臺電腦嘗試後，發現部分電腦同樣具有這一問題。

  隨後，通過多次嘗試發現，若在匯入這一初始取樣點圖層前，任意新增一幅「.png」格式圖片，軟體則將不會報錯，繼續正常執行。

  結合後續操作，個人認為這一問題可能是原始取樣點資料檔案中部分內容與ArcMap 10.2軟體不相容導致。

5.3 環境要素提取零值處理

  在對環境要素進行「多值提取至點」時，我原本將「點位置處的雙線性插值（可選）」選項選中。但這樣得到的提取結果中會出現個別點多數環境變數數值均為0的情況。

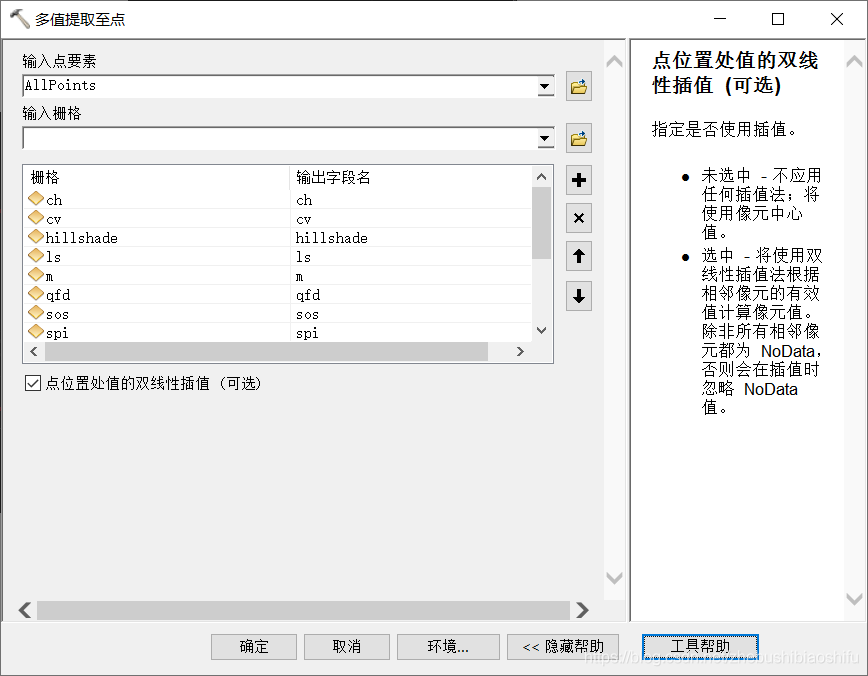
  因此，嘗試在ArcMap軟體中將提取後環境變數多為0的點（共四個）一同選中，檢視其分佈位置。可以發現，上述出現數值多0的點均分佈於沙洋縣邊界區域。

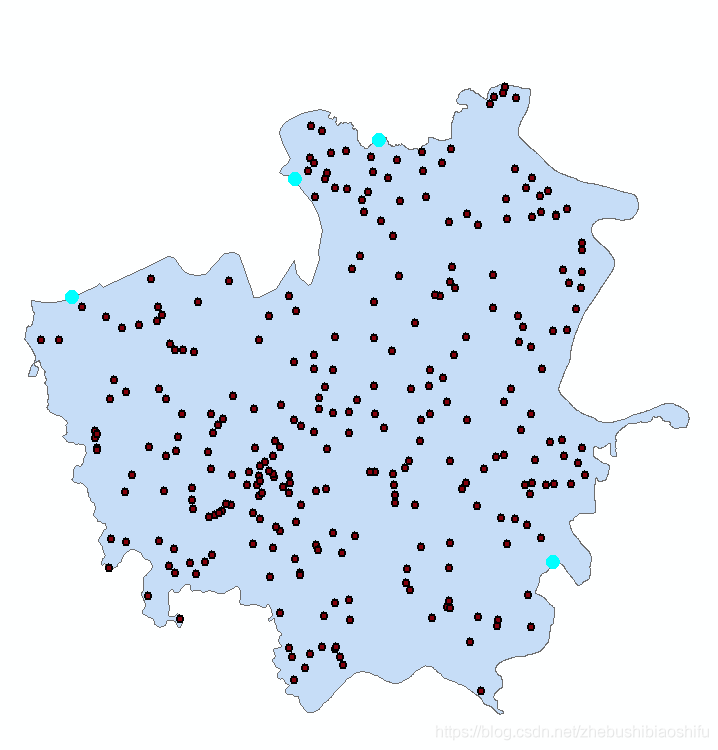
  即使用插值後，邊界點受到沙洋縣範圍外空白像元的影響，從而導致提取的環境變數為0。因此，取消選中上述插值功能，並再次執行「多值提取至點」操作；但隨後發現，這樣執行操作後依然仍有一點的各項環境變數數值提取結果多為0。

  同樣在ArcMap軟體中選中這一點，並放大。

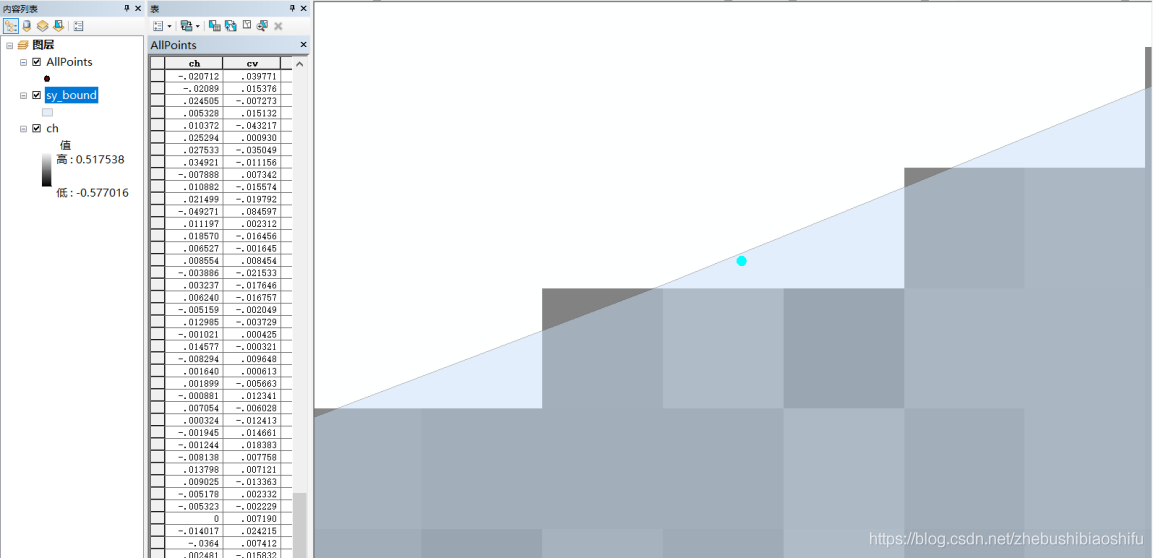
  可以看到，該點位於沙洋縣邊界圖層範圍內，而不位於環境變數柵格圖層範圍內——即處於二者之間。因此，該點在提取時無論是否使用插值方法，均會導致最終的提取結果多為0。

  由此，我選擇將該點作為異常值點，並在後續異常值剔除步驟中一併將其刪去。

5.4 相關性分析與迴歸方程結果對比

  在執行逐步線性迴歸前，我先利用皮爾遜相關性分析方法，對13個環境變數資料與土壤有機質含量之間的相關性加以衡量；隨後，利用逐步迴歸方法求出環境變數與土壤有機質含量的迴歸方程。具體相關性分析結果與迴歸方程結果已附於本文前述表2、表3處。

  由兩表所示結果可知，相關性分析所得結果與迴歸方程所得結果具有一定不相符之處。例如，相關性分析顯示，與土壤有機質含量具有較顯著相關關係的環境變數包括QFD、SOS、SPI、DEM90與β等，其餘環境要素與有機質含量之間相關性不顯著；而回歸模型中，卻包含了部分相關性不顯著的環境變數，如模型三中包括了m、α與WTI等。

  隨後通過網際網路等資源獲知，相關性分析僅針對某單一自變數進行其與因變數之間相關性的分析，即各環境變數在進行相關性分析時為獨立狀態；而逐步迴歸則是將模型內已有全部變數結合，作為整體來衡量模型與因變數之間的擬合關係。因此，針對二者不同的結果，應以逐步線性迴歸方法最終納入迴歸模型中的環境變數為準。

5.5 Box-Cox變換

  本文中，涉及到殘差的普通克里格與土壤有機質含量的普通克里格等。其中，後者由於均為正數，因此可適合大部分正態分佈轉換方法；而前者由於存在部分負值，從而受阻。

  其中，在針對不同模型對應殘差進行普通克里格計算時，考慮到Box-Cox變換依據冪引數選取的不同，具有兩種形式；因此誤認為其可以適用於存在負值的資料。而隨後的實踐中發現這一想法錯誤。

  因此，藉助MATLAB軟體「boxcox」函數的官方說明，進一步確定Box-Cox變換僅適用於正數情況。

5.6 迴歸克里格結果錯誤

  在進行迴歸克里格計算時，前期計算結果總和所得普通克里格土壤有機質含量插值結果有著較大差異。經過對比，發現所得迴歸克里格結果在整體趨勢上與普通克里格所得結果相反——迴歸克里格插值結果較大區域，其普通克里格結果反而較小；反之亦然。

  上圖即為出現問題的迴歸克里格插值結果。可以看到，這一結果與個人最終結果所呈現的有機質含量空間分佈趨勢正好相反。

  因此對這一問題進行多次重複操作等處理，但結果均表現出同樣的錯誤。隨後，考慮到所得結果與普通克里格結果正好為相反趨勢，因此對殘差加以檢查；從而發現由於殘差在計算時，錯將實測值與迴歸方程值之差誤寫作迴歸方程值與實測值之差。將這一問題改正後重新執行迴歸克里格插值，得到與普通克里格一致的結果。

  得到上述結果後進一步思考，進而引出又一問題——如前所述，一般地，往往認為迴歸克里格中，對結果起到較為重要作用的因素為空間趨勢項，而非殘差項。而為何在此處，由於殘差計算的錯誤導致最終迴歸克里格結果出現如此之大的差異？

  隨後，個人結合相關中、外文獻與本文前述土壤有機質含量經典統計學分析結果（表1），嘗試探究並行現問題所在。首先，迴歸克里格中起到重要影響作用的成分的確是空間趨勢項（這即是其較之普通克里格方法結果更加零碎、更好展示出細節的原因），而其影響具體有「多麼」重要，則需結合研究區域實際情況等加以判，其隨著目標變數的空間變異性特徵而發生變化。其次，上述錯誤相當於將殘差符號取反，即造成的影響為殘差原有比重的兩倍，進而對最終結果造成較大影響。

5.7 迴歸克里格結果異常值

  利用前述迴歸模型三進行迴歸克里格插值，所得結果中包含-140左右的負值。結合ArcMap軟體「識別」工具，對地圖中較低值區域加以數值獲取，發現其數值均為15左右，並未找出具體-140值所在。

  由此，針對這一異常值問題，個人判斷是由於迴歸方程納入了一些具有較低或較高值的環境變數，從而導致極個別迴歸模型結果圖層畫素出現異常值。由於該值較低，導致即使加入殘差項後亦並無明顯改進。隨後，嘗試利用模型二對應迴歸方程進行後續操作，問題得以解決。

  另一方面，前述模型三對應逐步迴歸過程中，所選用進入和除去的概率均較大，故其部分環境變數係數顯著性水平偏高（即數值較大）；選用模型二在避免異常值畫素出現的同時，同樣避免了這一顯著性水平問題。

5.8 研究區域水體辨別

  在本文中我們可以注意到，所研究區域沙洋縣境內水體較多——如其東北部邊界緊鄰漢江，南部區域為大面積的長湖，且境內包含金雞水庫、安窪水庫、潘集水庫等小型水庫，以及各類小型河流；因此，本次在利用普通克里格方法或迴歸克里格方法對研究區域土壤有機質含量進行插值計算時，水體部分自然需要剔除。

  一般地，為提取水體等區域，需要結合數位化後的、精細的土地利用現狀圖或相關遙感衛星影像等。而在本次操作中，個人暫未找到方便獲取、質量較好，且可在相關地學軟體中處理的資料等。因此，如前所述，在運用兩種克里格方法進行插值計算時，我並未將水體剔除。

  在本文操作部分進入尾聲、進行專題地圖製作時，我曾分別考慮利用相關圖片編輯軟體對水體中面積較大的長湖進行區分或利用實驗材料中NDVI資料提取水體，分別如下左、右圖所示。

  上述第一種方法，一方面由於水體為手動編輯，十分不嚴謹，不符合科研的嚴密性，使得實驗結果可靠性嚴重下降；另一方面，其仍未對沙洋縣其它水體加以區分。上述第二種方法，一方面水體與雲層、雪等NDVI數值均較小，在不瞭解對應遙感影象成像氣候條件情況下提取結果可靠性不高；另一方面，提取過程中所選NDVI閾值具有主觀性，閾值對應結果因而均有不確定性。因此，最終結果中放棄了對水體進行提取操作。而在其它可獲得相關資料的情況下，還需儘可能避免上述將水體納入土壤屬性插值範圍的情況。

  此外，可以藉助遙感影像，結合監督分類等方式對水體區域加以提取。監督分類的相關操作大家可以參考ENVI+ERDAS實現Hyperion葉綠素含量反演：經驗比值法、一階微分法。

參考文獻

[1] Zhang C, Yang Y. Can the spatial prediction of soil organic matter be improved by incorporating multiple regression confidence intervals as soft data into BME method?[J]. CATENA. 2019, 178: 322-334.

[2] Zhang S, Huang Y, Shen C, et al. Spatial prediction of soil organic matter using terrain indices and categorical variables as auxiliary information[J]. Geoderma. 2012, 171-172: 35-43.

[3] 曹祥會，龍懷玉，周腳根，等. 河北省表層土壤有機碳和全氮空間變異特徵性及影響因子分析[J]. 植物營養與肥料學報. 2016, 22(04): 937-948.

[4] 李龍，周飛，田傑，等. 地形因子對半乾旱地區土壤有機碳含量的影響[J]. 北方園藝. 2019(16): 104-109.

[5] 張國峰，楊立榮，瞿明凱，等. 基於地理加權迴歸克里格的日平均氣溫插值[J]. 應用生態學報. 2015, 26(05): 1531-1536.

[6] 姜勇，樑文舉，李琪. 利用與迴歸模型相結合的克里格方法對農田土壤有機碳的估值及製圖[J]. 水土保持學報. 2005(05): 99-102.

[7] 張若兮，楊勇，張楚天. 基於範疇型變數和貝葉斯最大熵的土壤有機質空間預測[J]. 土壤通報. 2015, 46(02): 312-318.

[8] 李愛華，柏延臣. 基於貝葉斯最大熵的甘肅省多年平均降水空間化研究[J]. 中國沙漠. 2012, 32(05): 1408-1416.