LeetCode買賣股票之一：基本套路(122)

歡迎存取我的GitHub

這裡分類和彙總了欣宸的全部原創(含配套原始碼)：https://github.com/zq2599/blog_demos

關於《LeetCode買賣股票》系列

在LeetCode上，有數道和買賣股票有關的題目，覆蓋了簡單、中等、困難，要求都是選擇低價時間買入、高價時間賣出，以求達到利潤最大化
這類題型的特點就是：典型的動態規劃題型，掌握套路後，越做越開心，就算難度是困難的題目，也能從容面對
於是，欣宸將此類題目聚集在一起，集中火力分析和解題，構成了《LeetCode買賣股票》系列，在該系列中，欣宸與您一同打好基礎，再將該型別題目逐個攻克，在LeetCode世界中做一回股神

本篇概覽

對之前的解題經歷做了認真回顧後，我這邊決定用第122題《買賣股票的最佳時機 II》作為系列的開篇，原因是此題在所有買賣股票的文章中最為典型：題目具備代表性，同時其他題目中奇怪的約束條件如凍結期、交易次數等，在122題中都不存在，寫出的狀態轉移方程可以作為其他題目的參考
接下來開始做題吧，先看題目

題目資訊

題號：122
難度：中等
描述

給你一個整數陣列 prices ，其中 prices[i] 表示某支股票第 i 天的價格。
在每一天，你可以決定是否購買和/或出售股票。你在任何時候最多只能持有一股股票。你也可以先購買，然後在同一天出售。
返回你能獲得的最大利潤。

範例 1：

輸入：prices = [7,1,5,3,6,4]
輸出：7
解釋：在第 2 天（股票價格 = 1）的時候買入，在第 3 天（股票價格 = 5）的時候賣出, 這筆交易所能獲得利潤 = 5 - 1 = 4 。
     隨後，在第 4 天（股票價格 = 3）的時候買入，在第 5 天（股票價格 = 6）的時候賣出, 這筆交易所能獲得利潤 = 6 - 3 = 3 。
     總利潤為 4 + 3 = 7 。

範例 2：

輸入：prices = [1,2,3,4,5]
輸出：4
解釋：在第 1 天（股票價格 = 1）的時候買入，在第 5 天 （股票價格 = 5）的時候賣出, 這筆交易所能獲得利潤 = 5 - 1 = 4 。
     總利潤為 4 。

範例 3：

輸入：prices = [7,6,4,3,1]
輸出：0
解釋：在這種情況下, 交易無法獲得正利潤，所以不參與交易可以獲得最大利潤，最大利潤為 0 。

提示：

1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104

核心問題分析

解題的關鍵，是搞清楚兩個最核心的問題：

我們要的是什麼？
變化有哪些？

第一個問題：我們要的是什麼？

認真審題後，我們要的東西可以這樣描述：第i天股市結束後手裡的最大利潤

第二個問題：有哪些變化？

很容易發現，一共有兩種變化：和行為無關、和行為有關

和行為無關的變化：是時間和股價，只要知道是第幾天，也就知道了股價，所以只要聚焦時間變化即可
和行為有關的變化：股票持有情況，即持有和不持有

確定dp定義

弄清楚上述兩個問題後，dp定義也就呼之欲出了：

dp陣列的值就是我們想要的東西
dp陣列的維度就是變化，一共有兩個變化，所以一共有兩個維度

於是，我們對dp陣列的定義如下圖
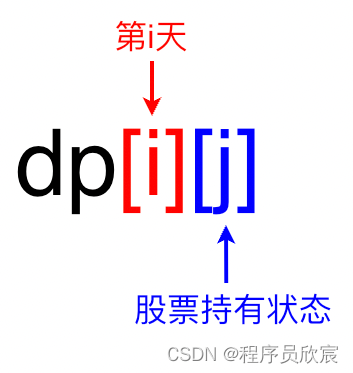
上圖中，i的取值好理解，表示第幾天，至於j，我們規定它只有兩個值：0和1,0代表不持有股票，1代表持有股票
下圖是個例子，很容易理解：第3天股市結束後，未持有股票時，手裡的最大利潤是123元

狀態轉移方程分析

要想寫出狀態轉移方程，首先要弄明白狀態是怎麼變化的，時間狀態自不必分析，它是客觀在變化的，我們要弄明白的是另一個狀態：股票持有狀態，嚴格來說要弄清楚兩點：

第i天股市結束後，如果手裡持有股票，這個股票是從哪來的？
第i天股市結束後，如果手裡沒有股票，為什麼手裡會沒有股票？

只要弄清楚上述兩個問題，狀態轉移方程也就出來了，接下來逐個分析

手裡持有股票的原因

第i天股市結束後，如果手裡持有股票，有兩種可能：

第i天之前持有股票，到了第i天啥也不做，此時：dp[i][1]=dp[i-1][1]
第i天之前不持有股票，在第i天購買了，此時：dp[i][1]=dp[i-1][0]-price[i]，因為購買要花錢，所以用手裡的錢減去當天股價

我們要的是最大利潤，所以應該取上述兩種情況的最大值
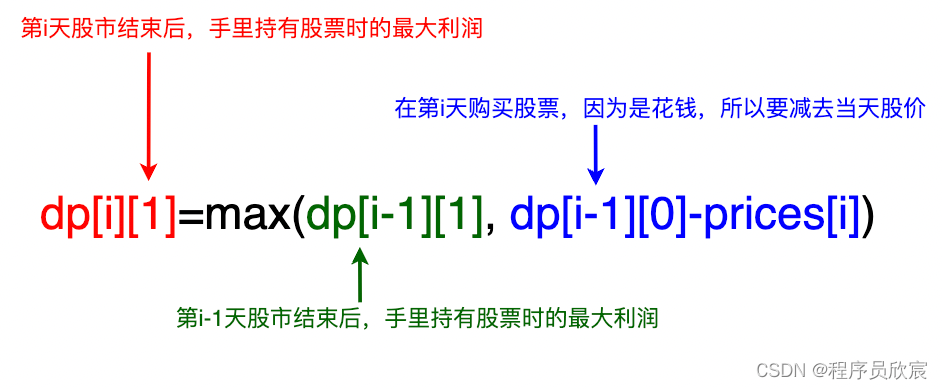
現在可以寫出dp[i][1]的表示式了：dp[i][i]=Math.max(dp[i-1][1], dp[i-1][0]-price[i])
一圖勝千言，看過下圖您就一定明白了

手裡未持有股票的原因

接下來繼續分析，第i天股市結束後如果手裡沒有股票，有兩種可能導致：

第i天之前未持有股票，到了第i天啥也不做，此時：dp[i][0]=dp[i-1][0]
第i天之前持有股票，在第i天賣出，此時：dp[i][0]=dp[i-1][1] + price[i]，因為賣出股票會換來錢，所以這裡用手裡的錢加上當天股價

我們要的是最大利潤，所以應該取上述兩種情況的最大值
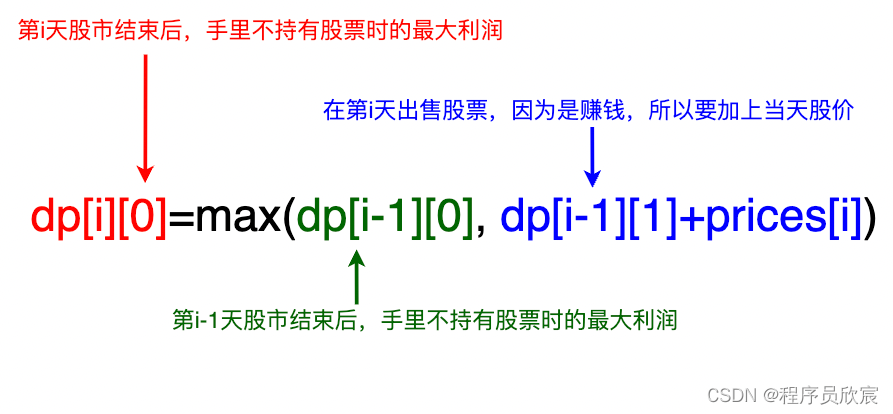
現在可以寫出dp[i][0]的表示式了：dp[i][0]=Math.max(dp[i-1][0], dp[i-1][1]+price[i])
一圖勝千言，看過下圖您就一定明白了
狀態轉移方程已經出來了，接下來按部就班寫好程式碼提交即可

編碼

有了上面的分析，相信此刻您也能流暢的完成編碼了，參考程式碼如下

class Solution {
    public int maxProfit(int[] prices) {

        int[][] dp = new int[prices.length][2];

        // 第0天股市結束後，如果手裡沒有股票，那就是沒有購買過，此時最大利潤只能等於0
        // 初始化為0的程式碼可以省去
        // dp[0][0] = 0;

        // 第0天股市結束後，如果手裡有股票，那就是當前購買的，此時最大利潤就是負數
        dp[0][1] = -prices[0];

        for (int i=1;i<prices.length;i++) {
        	// 第i天股市結束時，手裡沒有股票的原因有兩個：
        	// 1. 之前就沒有股票，第i天啥樣沒做
        	// 2. 之前有股票，第i天賣出
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            // 第i天股市結束時，手裡有股票的原因有兩個：
        	// 1. 之前就有股票，第i天啥樣沒做
        	// 2. 之前沒有股票，第i天買入
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
        }

        // 第i天結束後，手裡不持有股票的最大利潤就是返回值
        return dp[prices.length-1][0];
    }
}

提交程式碼，如下所示，雖然AC了，但是速度很一般，超過26.27%的提交，顯然還有優化空間

優化

回顧上述程式碼中，dp[i][0]和dp[i][1]都是通過dp[i-i][0]和dp[i-1][1]計算出來的，如此看來，這個dp二維陣列似乎有些浪費，用下面這四個變數足矣

prevWithStock：前一天股市結束後，手裡有股票時的最大利潤
prevWithoutStock：前一天股市結束後，手裡沒有股票時的最大利潤
currentWithStock：當天股市結束後，手裡有股票時的最大利潤
currentWithoutStock：當天股市結束後，手裡沒有股票時的最大利潤

優化後的程式碼如下

class Solution {
    public int maxProfit(int[] prices) {
        // 第0天股市結束後，如果手裡有股票，那就是當前購買的，此時最大利潤就是負數
        int prevWithStock = -prices[0];

        // 第0天股市結束後，如果手裡沒有股票，那就是沒有購買過，此時最大利潤只能等於0
        int prevWithoutStock = 0;

        // 當天股市結束後，如果手裡有股票時的最大利潤
        int currentWithStock;

        // 當天股市結束後，如果手裡沒有股票時的最大利潤
        int currentWithoutStock = 0;
        
        for (int i=1;i<prices.length;i++) {
            currentWithoutStock = Math.max(prevWithoutStock, prevWithStock + prices[i]);
            currentWithStock = Math.max(prevWithStock, prevWithoutStock - prices[i]);
            prevWithStock = currentWithStock;
            prevWithoutStock = currentWithoutStock;
        }

        // 第i天結束後，手裡不持有股票的最大利潤就是返回值
        return currentWithoutStock;
    }
}

再次提交，稍微提升了一點
至此，買賣股票的基本套路，以及狀態轉移方程設計思路和實現，咱們已經學習到了，接下來的文章中，都會基於這個思路去設定狀態轉移方程
當然了，此刻您應該還有個疑問：為何速度的排名如此之低？接下來咱們來看看落後的原因

為啥排名不高？

這道題本身也有一些特殊：除了動態規劃，貪婪演演算法也能解
以prices={1, 2, 3}為例，聰明的您應該看出來了，如果1買入，3賣出，得到的利潤等於2，屬於最大利潤
題目有個約束：一天不能既買入又賣出，如果跳出這個約束，那就可以做到1買入2賣出，然後2買入3賣出，利潤還是2！
至於能不能將3-1轉化成(3-2)+(2-1)呢？當然可以，減去2再加上2，對原題的結果毫無影響，卻可以改變程式碼流程，如下所示，每當買入賣出能賺錢時，就將外掛累加起來，這樣的計算中，相比前面的程式碼，每次迴圈中的計算量明顯減少了

class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length<2) {
            return 0;
        }

        int total = 0;

        for (int i=1;i<prices.length;i++) {

            if (prices[i]>prices[i-1]) {
                total += prices[i] - prices[i-1];
            }

        }

        return total;
    }
}

再次提交，這回超越了百分百
至此又得出一個結論：本題用動態規劃做並沒有錯，也不是動態規劃程式碼沒寫好，而是有更高效的貪婪演演算法恰巧也能解決此問題
經過本篇實戰，相信您對動態規劃以及股票買賣問題都有了更深的理解，接下來，繼續挑戰其他股票買賣問題，在LeetCode世界中向著股神前進

歡迎關注部落格園：程式設計師欣宸

學習路上，你不孤單，欣宸原創一路相伴...