Semi-Supervised Domain Adaptation with Source Label Adaptation

具有源標籤適應的半監督域適應

原文連結

Abstract

文章指出當前的半監督域適應（Semi-Supervised Domain Adaptation, SSDA）方法通常是通過特徵空間對映和偽標籤分配將目標資料與標記的源資料對齊，然而，這種面向源資料的模型有時會將目標資料與錯誤類別的源資料對齊，導致分類效能降低。

本文提出了一種用於SSDA的新型源自適應正規化，該正規化通過調整源資料以匹配目標資料，從而提高分類效能。

文中所提出的模型可以有效清除源標籤內的噪聲，並在基準資料集上表現優於其他方法。

1. Introduction

前人從理論和演演算法的角度廣泛地研究了非監督域適應（Unsupervised DA, UDA），其中目標域的標籤是無法存取。近期，半監督域適應（SSDA）受到了關注，半監督域適應是一種允許存取部分目標標籤的DA，這種改變簡單、現實符合應用需求。

最經典的SSDA策略便是S+T：使用源資料和未標記的目標資料並採用標準交叉熵損失函數訓練模型。但由於不同資料分佈差異，該策略總是遇到域轉移問題。為解決這個問題，許多SOTA（state-of-the-art algorithm）試圖探索充分利用未標記的目標資料，以便目標分佈可以與源分佈保持一致。

最近，幾種半監督學習（Semi-Supervised Learning, SSL）演演算法已經應用至SSDA來對未標記的資料進行正則化，例如熵最小化（entropy minimization）、偽標記（pseudo-labeling）、和一致性正則化（consistency regularization）。雖然這些演演算法發展了較長時間，但它們通常要求目標資料與源資料有一定的語意相似性。因此，如果S+T空間未對準將很難表現好。如圖1上方所示：

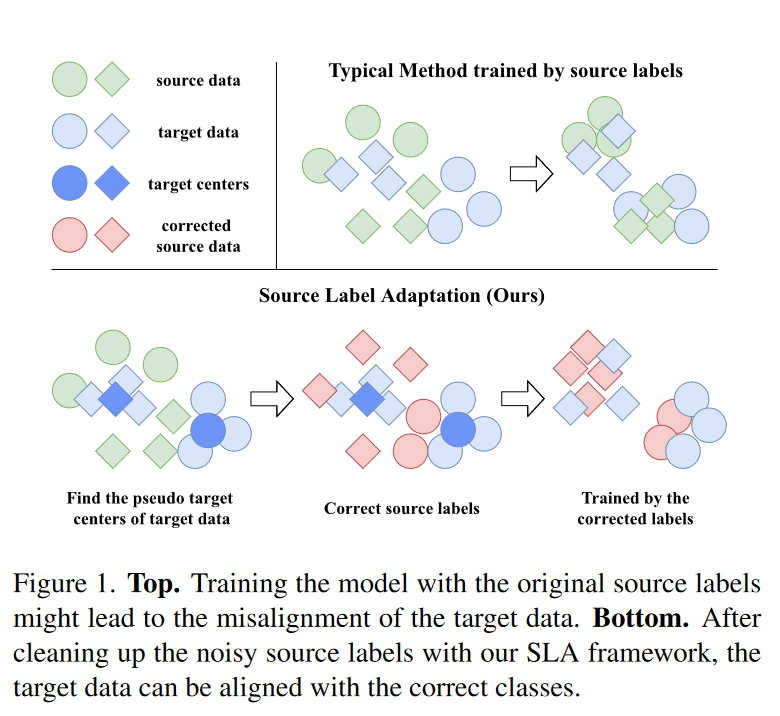
作者在文中舉例認為依賴源標籤的演演算法例如S+T會誤導模型學習錯誤的類。因此源標籤可以被視為目標分類中帶噪聲的標籤，SSDA更像是一個噪聲標籤學習（Noisy Label Learning, NLL）：有大量的噪聲標籤（源標籤）和少量的乾淨標籤（目標標籤）。

作者借鑑標籤校正的思想（藉助另一個模型來清理噪聲標籤），提出了源標籤適應框架（Source Label Adaptation, SLA）,如圖1下部分所示。作者構造了一個標籤適應元件提供了目標資料的檢視並在每一次迭代中動態清理帶噪聲的源標籤。之前的研究是利用未標記的目標資料，而作者是研究如何使用適應的標籤來訓練源資料以更好地適應理想的目標空間。這種源自適應正規化與現有的SSDA演演算法背後的核心思想完全正交，因此可以將兩者結合達到更好的效果。

作者總結了三點貢獻：

經典的面向源的方法如S+T及其派生的演演算法任然會受到有偏差的特徵空間的影響，為了擺脫困境，作者提議修改原始源標籤來使源資料適應目標空間。
作者將DA當作是NLL的特定情況並提出了一種新穎的源適應正規化，作者的框架能夠簡單地與現用的演演算法結合並提高效能。
作者展示SLA框架與SSDA的SOTA演演算法結合。該框架在兩個主要測試資料集上顯著改進了現有的演演算法，指引瞭解決DA問題的新方向。

問題設定

DA專注於m維度的K類分類任務，

輸入空間：\(X\subseteq\mathbb{R}^m\)
標籤集合：\(\{1,2,\dots,K\}\)
在概率單純形上\(\triangle^K\)上定義標籤空間\(Y\),標籤\(y=k\in\{1,2,\cdots,K\}\)相當於獨熱編碼向量，\(y\in Y\)
設立\(X\times Y\)的兩個域：源域\(D_s\)，目標域\(D_t\)
在SSDA，對帶標籤的源資料進行一定數量的取樣：\(S=\{(x^s_i,u^s_i)\}_{i=1}^{|S|}\)，資料來自\(D_s\)；對帶標籤的目標資料進行取樣：\(L=\{(x^{\ell}_i,u^{\ell}_i)\}_{i=1}^{|L|}\)，資料來自\(D_t\)；以及未標籤的目標資料：\(U=\{x^u_i\}^{|U|}_{i=1}\)，資料來自\(D_t\)在\(X\)的邊緣分佈。
通常，\(|L|\)是遠小於\(|S|\)和\(|U|\)。
目標是訓練帶有\(U\)、\(S\)、\(L\)的SSDA模型\(g\)，使其在目標域上表現良好。

半監督學習

SSDA可以被視為UDA的簡單現實形式。SSDA演演算法通常包含三個損失函數：

\[\mathcal{L}_{SSDA}=\mathcal{L}_s+\mathcal{L}_{\ell}+\mathcal{L}_u \tag{1} \]

\(\mathcal{L}_s\)是由源資料得到的損失；\(\mathcal{L}_{\ell},\mathcal{L}_u\)分別表示來自標記的和未標記目標資料的損失。
由於問題的相似性，近期的研究為了解決SSDA問題借鑑了SSL的技術，提出了一種熵最小化的變體，以明確地將目標資料與源叢集對齊。

Deep co-training with task decomposition for semisupervised domain adaptation一文中，將SSDA拆解為SSL和UDA任務。兩個不同的子任務分別產生偽標籤，並通過協同訓練相互學習。

Cross-Domain Adaptive Clustering for Semi-Supervised Domain Adaptation一文中通過測量成對特徵相似性將目標特徵分組。

Multi-level Consistency Learning for Semi-supervised Domain Adaptation一文中利用三個不同級別的一致性正則化執行域對齊。

此外，這兩篇文章都應用了帶有資料增強的偽標籤來增強其效能。從目標資料的角度來看，源標籤可能顯得嘈雜，作者提出了一個源自適應框架以逐漸使源資料適應目標空間，這種框架可應用於上述幾種演演算法提高效能。

噪聲標籤學習

機器學習演演算法的結果高度依賴於資料集的質量。為解決噪聲標籤，TRAINING DEEP NEURAL NETWORKS ON NOISY LABELS WITH BOOTSTRAPPING一文中提出一種平滑機制，降噪生變標籤與與自我預測相結合。

Joint Optimization Framework for Learning with Noisy Labels將乾淨標籤建模為可訓練引數，並設計聯合優化演演算法來交替更新引數。

作者在，TRAINING DEEP NEURAL NETWORKS ON NOISY LABELS WITH BOOTSTRAPPING和Meta Label Correction for Noisy Label Learning的啟發下，構造了一個簡單框架，可以有效地構建標籤適應模型來糾正噪聲標籤。

3. Proposed Framework

3.1 將域適應作為噪聲標籤學習

在域適應中，尋找一個理想的模型\(g^*\)，它可以最小化未標記的目標風險。理想情況下，目標空間中源範例\(x^s_i\)最合適的標籤是\(g^*(x^s_i)\)，理想的源損失\(\mathcal{L}^s_i\)為：

\[\mathcal{L}^*_s(g|S)=\frac{1}{|S|}\sum^{|S|}_{i=1}H(g(x^s_i),g^*(x^s_i))\tag{2} \]

其中\(H\)為測量兩個分佈之間的交叉熵

結合帶標籤的目標損失\(\mathcal{L}_\ell\)，作者將\(\mathcal{L^*_s}\)和\(\mathcal{L}_\ell\)訓練的模型稱為理想適應的S+T

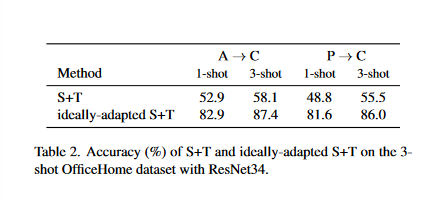
表中的測試結果展示了適應源標籤的潛力——理想適應的S+T與標準的S+T有著顯著的差異，這是僅修改源標籤帶來的影響。但是實踐中只能得到近似理想模型，為解決該問題，作者將原始源標籤視為理想標籤的噪聲版本，將DA視為NLL模型。

首先是通過TRAINING DEEP NEURAL NETWORKS ON NOISY LABELS WITH BOOTSTRAPPING提出的方法幫助糾正源標籤。具體來說，對於每一個源範例\(x^s_i\)，構建修正源標籤\(\hat{y}^s_i\)，修正標籤由帶比率\(\alpha\)的兩部分組成：原始標籤\(y^s_i\)和當前模型\(g\)的預測。

\[\hat{y}^s_i=(1-\alpha)\cdot y^s_i+\alpha\cdot \color{red}{g(x^s_i)}\tag{3} \]

於是，修正的源損失\(\hat{\mathcal{L}}_s\)為

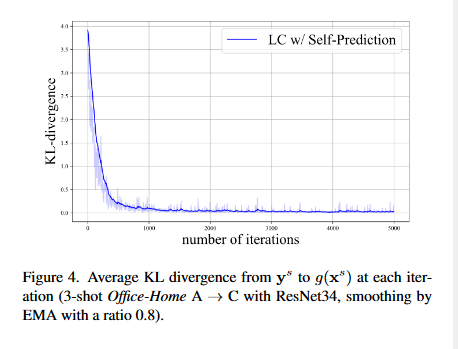
\[\hat{\mathcal{L}}_s(g|S)=\frac{1}{|S|}\sum^{|S|}_{i=1}H(g(x^s_i),\hat{y}^s_i)\tag{4} \]

但是在DA中，這種方式可能不適用，因為模型通常會過度擬合源資料使得\(g(x^s_i)\approx y^s_i\)，也就是修改後的源標籤\(\hat{y}^s_i\)會與原始源標籤\(y^s_i\)幾乎相同。

圖4中展示了當使用自預測進行標籤校正時，經過2000次迭代\(y^s\)和\(g(x^s)\)的KL散度幾乎一致。這種情況下，進行校正相當於不進行校正。

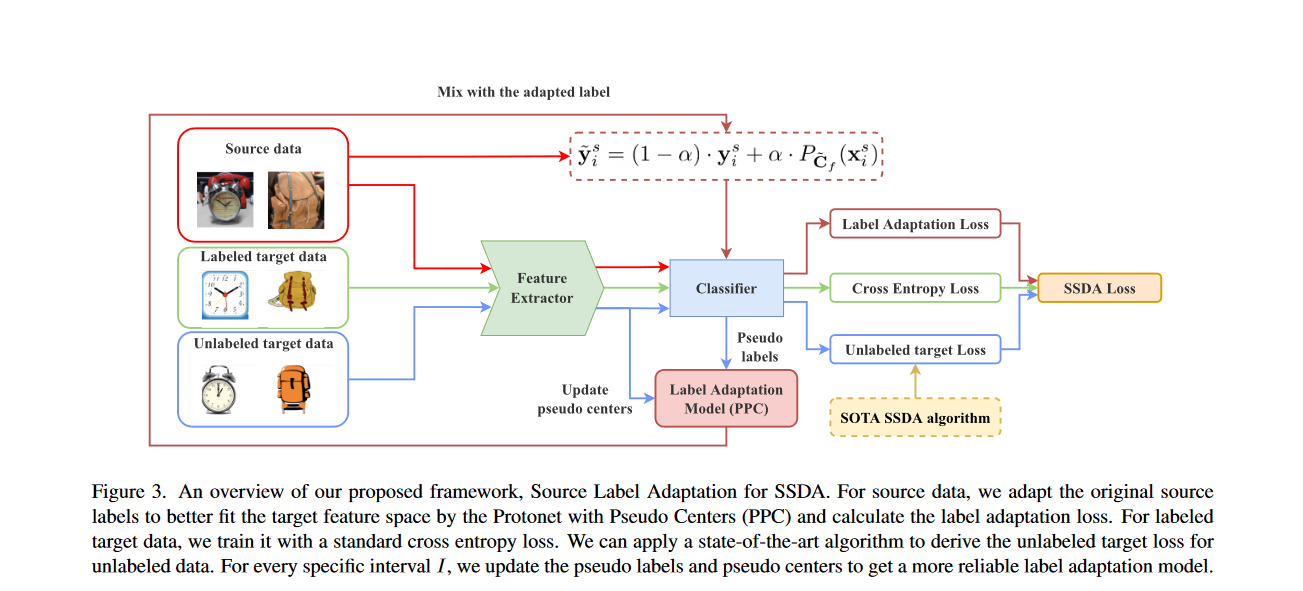
為了充分利用修正後的標籤，需要消除對原資料的監督。由於理想的乾淨標籤是理想模型\(g^*\)的輸出，因此需要一個近似理想模型的標籤適應模型\(g_c\)使源標籤適應目標資料。將適應標籤\(\tilde{y}^s_i\)定義為原始標籤\(y^s_i\)和\(g_c\)輸出之間的凸組合：

\[\tilde{y}^s_i=(1-\alpha)\cdot y^s_i+\alpha\cdot \color{red}{g_c(x^s_i)}\tag{5} \]

3.2 具有偽中心的Protonet

在半監督學習中，雖然可以存取部分目標標籤，但由於數量有限可能會遇到嚴重的過擬合問題，因此選擇使用原型網路（protonet）克服樣本數量少的問題。

給定資料集\(\{x_i,y_i\}^N_{i=1}\)，特徵提取器\(f\)。\(N_k\)表示用\(k\)標記的資料的數量，\(k\)的原型被定義為具有相同類的特徵中心：

\[c_k=\frac{1}{N_k}\sum^N_{i=1}\mathbb{I}\{y_i=k\}\cdot f(x_i)\tag{6} \]

令\(C_f=\{c_1,\dots,c_K\}\)使用特徵提取器\(f\)收集所有中心。將\(P_{C_f}:X\mapsto Y\)定義為帶中心\(C_f\)的protonet模型：

\[P_{C_f}(x_i)_k=\frac{\exp(-d(f(x_i),c_k)\cdot T)}{\sum^K_{j=1}\exp(-d(f(x_i),c_j)\cdot T)}\tag{7} \]

此處，\(d:F\times F\mapsto[0,\infty)\)表示特徵空間\(F\)的距離度量，通常是歐氏距離（L2距離）；\(T\)是控制輸出平滑度的超引數，當\(T\to0\)時，protonet的輸出將接近均勻分佈。

當\(d\)測量歐氏距離時，protonet相當於在\(F\)上具有特定引數化的線性分類器。由於帶標記中心的protonet是由目標資料的角度構建的，因此能減少3.1中提到的問題。

然而，在protonet中，理想中心\(C^*_f\)應通過未標記的目標資料集\(\{x^u_i\}^{|U|}_{i=1}\)。

對於當前模型，未標記目標範例\(x^u_i\)的偽中心\(\tilde{y}_i^u\)為

\[\tilde{y}_i^u=\argmax_kg(x^u_i)_k \]

使用偽標籤\(\{x^u_i,\tilde{y}_i^u\}^{|U|}_{i=1}\) 匯出未標記的目標資料後，通過式（6）得到偽中心\(\tilde{C_f}\)，並通過式（7）進一步定義具有偽中心的protonet（Protonet with Pseudo Centers, PPC）\(P_{\tilde{C}_f}\)。

表3中對比了S+T訓練的特徵空間分別從理想中心\(C^*_f\)到標記目標中心\(C^{\ell}_f\)和偽中心\(\tilde{C_f}\)的L2距離，這意味著偽中心確實更接近理想中心。

將PPC作為標籤適應模型，修改後的標籤\(\tilde{y}_i^S\)變為：

\[\tilde{y}_i^s=(1-\alpha)\cdot y_i^s+\alpha\cdot \color{red}{P_{\tilde{C}_f}(x_i^s)}\tag{9} \]

3.3 用於SSDA的源標籤適應

作者用標準交叉熵損失代替典型的源損失。對於每一個源範例帶有標籤\(y^s_i\)的\(x^s_i\)首先通過式（9）計算修正源標籤\(y_i^s\)。因此標籤的適應損失\(\tilde{L}_S\)：

\[\tilde{\mathcal{L}}_S(g|S)=\frac{1}{|S|}\sum_{|S|}^{i=1}H(g(x_i^s),\tilde{y}_i^s)\tag{10} \]

作者的框架源標籤適應（Source Label Adaptation, SLA）可通過一下損失函數進行訓練：

\[\mathcal{L}_{SSDA\space w/SLA}=\tilde{\mathcal{L}}_s+\mathcal{L}_{\ell}+\mathcal{l}_u \tag{11} \]

\(\mathcal{L}_\ell\)是目標資料的損失函數，也可以選用標準的交叉熵損失函數。對於未標記的目標資料\(\mathcal{L}_u\)的損失函數，可以採用任何SOTA，作者的框架可以輕鬆地與其他方法耦合但不產生矛盾。

實現細節

預處理（熱身）階段：框架依賴於預測的偽標籤的質量。然而，初始模型的預測可能存在噪聲。因此，需要引入一個超引數\(W\)進行預熱，以獲得更穩定的偽標籤。在預熱階段，使用原始源標籤正常訓練我們的模型。具體來說，在第\(e\)次迭代時，我們計算修改後的源標籤\(\tilde{y}^s_i\)如下：

\[\tilde{y}^s_i= \begin{cases} y^s_i,\ \mathrm{if}\ e \le W \\ (1-\alpha)\cdot y_i^s+\alpha\cdot P_{\tilde{C}_f}(x_i^s),\ \mathrm{otherwise} \end{cases}\tag{12} \]

動態更新：特徵空間和預測的偽標籤在訓練階段不斷演變，通過更新偽標籤和中心，目標是確保投影的偽中心在整個訓練階段保持其準確性或正確性。實際中通過式（8）更新偽標籤；對於每個特定區間\(I\)，通過式（6）使用當前的特徵提取器\(f\)更新新中心。

4. Experiments

作者選用了兩個測試資料集評估了提出的SLA框架：Office-Home和DomainNet。Office-Home主要用於測試無監督域適應和半監督域適應，包含了四個領域：藝術（A），剪下畫（C），產品（P）和真實（R），共65個領域；DomainNet最初設計用於對多元域適應方法進行測試，選取了四個域：真實（R）、剪下畫（C）、油畫（P）和素描（S）以及126個類，為SSDA構建更清晰的資料集。

作者將自己的框架與\(MME\)和\(CDAC\)演演算法結合，分別命名為\(MME+SLA\)和\(CDAC+SLA\)，為了對照比較，骨幹網路選擇\(ResNet34\)並預訓練於ImageNet-1K資料集。並設計超引數：式（12）中混合比率\(\alpha=0.3\)，式（7）中溫度引數\(T=0.6\)，3.3小節提到的區間\(I=500\)，預熱階段的式（12）中，對於在Office-Home資料集，MME的\(W=500\)，CDAC的\(W=3000\)；對於在DomainNet資料集，MME的\(W=3000\)，CDAC的\(W=50000\)。

在預熱階段之後，重新整理學習率，以便使用更高的學習率更新標籤適應損失；所有的超引數都可通過論證實驗進行適當調整。對於每個子任務，進行了三次實驗。

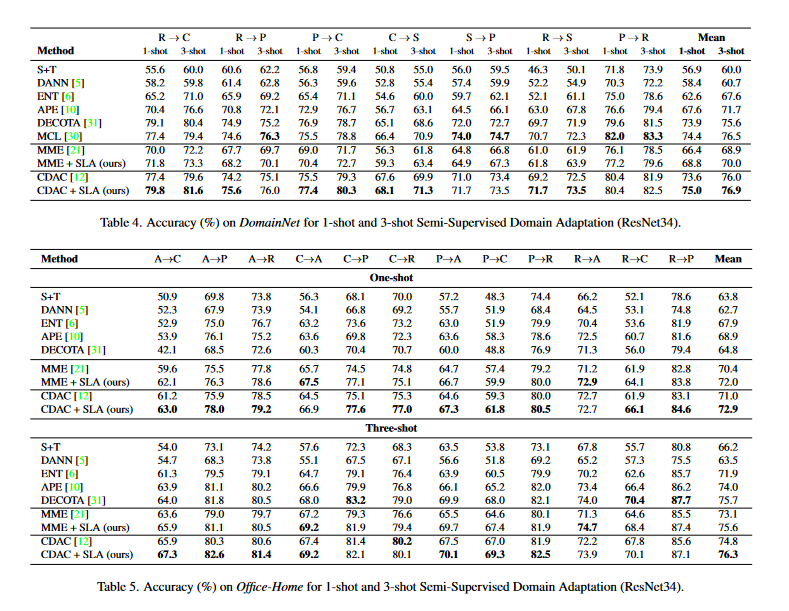
表4中作者的方法在DomainNet上對於應用了SLA的MME和CDAC幾乎所有的例子都得到了提升。同樣的，表5中作者的方法在Office-Home上對於應用了SLA的MME和CDAC幾乎所有的例子都得到了提升。

作者之後還對部分超引數進行對照試驗，確定合適的超引數選擇，這裡不再贅述。

5. Conclusion

本文展現了一種通用框架——具有源標籤適應的半監督域適應。
要仔細重新審視源資料的使用。
從目標資料的角度來看，源資料標籤可能含有噪聲。作者將域適應視為噪聲標籤學習，並使用帶有偽標籤的Protonet預測結果糾正源資料標籤（原文強調，作者解決的是一個正交（orthogonal）問題，現有的方法主要使目標資料與源資料保持一致，而論文的方法側重於校正源資料的噪聲標籤）。
實驗結果證明：將該框架應用於幾種SSDA的SOTA，能夠進一步提高效能。當由於每個類標記的資料較少，標記的目標資料中心\(C^{\ell}_f\)距離理想中心\(C^*_f\)較遠，因此建議使用偽中心代替。

噪聲標籤學習（Noisy Label Learning）：是指在監督機器學習任務中，訓練資料的標籤（即真實輸出）存在一定程度的錯誤、不確定性或噪聲的情況下，如何有效地訓練模型以獲得良好的效能。這種情況可能是因為資料收集過程中人為錯誤、資料註釋不準確、標註者主觀性等原因導致的。

ProtoNet（Prototype Network）：ProtoNet 是一種用於Few-shot學習的模型，最早由Snell等人在論文 "Prototypical Networks for Few-shot Learning" 中提出。它的核心思想是通過計算每個類別的"原型"來進行分類。原型是指在特徵空間中，對每個類別的樣本特徵求平均所得到的向量。在測試時，新樣本將與各個類別的原型進行比較，從而選擇最接近的類別作為預測結果。這種方法能夠在少樣本情況下進行有效分類。

Pseudo Centers（偽中心）：Pseudo Centers 是一個類似原型的概念，它是在Few-shot學習中使用的一種補充方法。在某些情況下，資料分佈可能不是完全均勻的，甚至可能有一些離群點。Pseudo Centers 的目的是為每個類別生成一組中心點，不同於原型，它們不僅考慮樣本的平均特徵，還考慮到其他特徵，如中心、方差等，從而更好地捕捉資料分佈的情況。

論文精讀：帶有源標籤自適應的半監督域適應（Semi-Supervised Domain Adaptation with Source Label Adaptation）