技術文章 » VINS中的重力-尺度-速度初始化（2）

VINS中的重力-尺度-速度初始化（2）

2023-09-05 18:00:43

VINS中的重力-尺度-速度初始化（2）

細化重力

\(\quad\)上一篇文章中得到的 \(g\) 一般是存在誤差的。因為在實際應用中，當地的重力向量的模一般是已知固定大小的（所以只有兩個自由度未知），而我們在前面求解時並沒有利用這個條件，因此最後計算出來的重力向量很難剛好滿足這個條件。於是，在vins的初始化中，還會對得到的重力向量進行修正。

\(\quad\)首先，作者對重力向量進行引數化：

\[\hat{g}=\|g\| \overline{\hat{g}}+w_{1} b_{1}+w_{2} b_{2}=\|g\| \overline{\hat{g}}+\vec{b}^{3 \times 2} w^{2 \times 1} \]

其中，\(\overline{\hat{g}}\)是上一步中估計得到的重力向量方向的單位向量，\(b_1\)與\(b_2\)是另外兩個單位向量，是\(\overline{\hat{g}}\)切平面上的兩個互相垂直的單位向量，獲得方式如下：

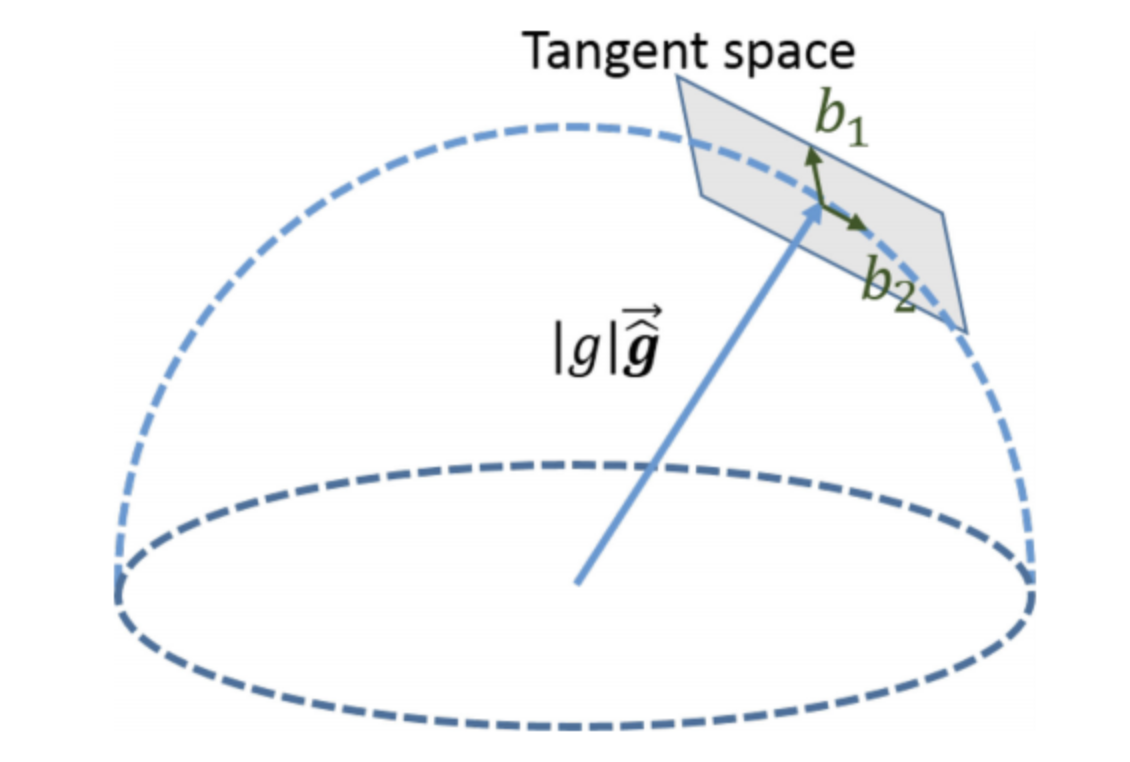
此時我們可以從上面的式子知道，原本三維的優化變數 \(g^{c 0}\) 已經可以使用兩維的 \(w^{2 \times 1}\) 替代。參考上一節的推導，待優化變數變成了

\[\left[\begin{array}{c} v_{b_{k}}^{b_{k}} \\ v_{b_{k+1}}^{b_{k+1}} \\ w^{2 \times 1} \\ s \end{array}\right] \]

最後得到的觀測方程也變為了

\[\left[\begin{array}{cccc} -I \Delta t_{k} & 0 & \frac{1}{2} R_{c_{0}}^{b_{k}} \Delta t_{k}^{2} \vec{b} & R_{c_{0}}^{b_{k}}\left(p_{c_{k+1}}^{c_{0}}-p_{c_{k}}^{c_{0}}\right) \\ -I & R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} & R_{c_{0}}^{b_{k}} \Delta t_{k} \vec{b} & 0 \end{array}\right]\left[\begin{array}{c} v_{b_{k}}^{b_{k}} \\ v_{b_{k+1}}^{b_{k+1}} \\ w \\ s \end{array}\right]=\left[\begin{array}{c} \alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}-\frac{1}{2} R_{c_{0}}^{b_{c}} \Delta t_{k}^{2}\|g\| \hat{\hat{g}} \\ \beta_{b_{k+1}}^{b_{k}}-R_{c_{0}}^{b_{k}} \Delta t_{k}\|g\| \hat{g} \end{array}\right] \]

基於新得到的觀測方程（可以使用LDLT分解求解），我們可以通過重力約束不斷地對初始化結果進行修正，迭代對其 進行求解（vins中迭代了4次），最後得到一個修正後的初始化結果。

與世界座標系對齊

這一步一般是最後一步，一般世界座標系選擇的是東北天座標系。則這個對齊操作就是得到將重力向量旋轉到Z軸上的旋轉矩陣，這個旋轉矩陣就是將原本座標變換到世界座標系（東北天座標系）的變換矩陣。

找到這個變換矩陣後，接下來就是使用這個變換矩陣將位姿，速度等狀態資訊都變換到世界座標系下。

加速度計bias

通過上面的閱讀，我們會發現在vins的初始化中並沒有對加速度計的bias進行估計，感覺對於超定的方程，多計算一個加速度計的bias好像也不是什麼難事，，而且建模應該會更準確。在這個初始化工作的論文中其實有解釋原因：

  1. 通過模擬實驗證明，如果運動不劇烈，加速度計的bias很難被觀測出來；
  2. 忽略加速計的bias對估計其他初始值的影響不大；
  3. 加速度計的bias是可以通過之後的VIO緊耦合優化，慢慢估計出來的；

參考資料