圖解Spark Graphx基於connectedComponents函數實現連通圖底層原理

原創/朱季謙

第一次寫這麼長的graphx原始碼解讀，還是比較晦澀，有較多不足之處，爭取改進。

一、連通圖說明

連通圖是指圖中的任意兩個頂點之間都存在路徑相連而組成的一個子圖。

用一個圖來說明，例如，下面這個叫graph的大圖裡，存在兩個連通圖。

左邊是一個連線圖，該子圖裡每個頂點都存在路徑相連，包括了頂點：{(5L, "Eve"), (7L, "Grace"), (1L, "Alice"), (2L, "Bob"), (3L, "Charlie")}。

右邊同樣是一個連線圖，該子圖裡每個頂點都存在路徑相連，包括了頂點：{(8L, "Henry")，(9L, "Ivy")，(6L, "Frank")}。

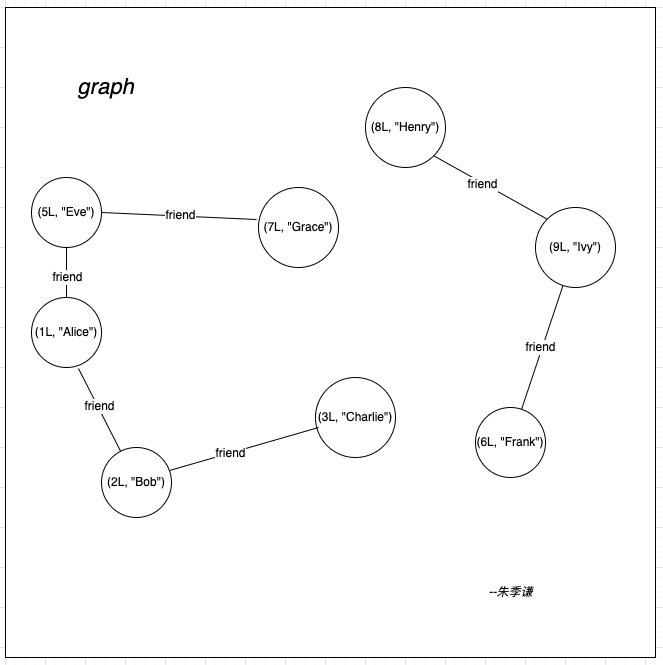
在現實生活裡，這兩個子圖就相當某個社群裡的關係網，在Spark Graphx裡，經常需要處理這類關係網的操作，那麼，在一個圖裡如何得到各個子圖的資料呢？

這時，就可以使用到Spark Graphx的connectedComponents函數，網上關於它的介紹，基本都是說它是Graphx三大圖演演算法之一的連通元件。

連通元件是指圖中的一組頂點，每個頂點之間都存在路徑互相關聯，也就是前面提到圖中的子圖概念。

通俗解釋，就是通過這個函數，可以將每個頂點都關聯到連通圖裡的最小頂點，例如，前面提到的子圖{(8L, "Henry")，(9L, "Ivy")，(6L, "Frank")}，在通過connectedComponents函數處理後，就可以得到每個頂點關聯到該子網的最小頂點ID。該子圖裡的最小頂點ID是6L，那麼，可以處理成以下資料{(8L，6L)，（9L，6L），(6L，6L)}。既然屬於同一個子圖的各個頂點都關聯到一個共同的最小頂點，不就意味著，通過該最小頂點，是可以按照分組的操作，將同一個最小頂點的資料都分組到一塊，這樣，就能提取出同一個子圖的頂點集合了。

二、案例說明

基於以上的圖頂點和邊資料，建立一個Graphx圖——

val conf = new SparkConf().setMaster("local[*]").setAppName("graphx")
val ss = SparkSession.builder().config(conf).getOrCreate()

// 建立頂點RDD
val vertices = ss.sparkContext.parallelize(Seq(
  (1L, "Alice"),
  (2L, "Bob"),
  (3L, "Charlie"),
  (5L, "Eve"),
  (6L, "Frank"),
  (7L, "Grace"),
  (8L, "Henry"),
  (9L, "Ivy")
))

// 建立邊RDD
val edges = ss.sparkContext.parallelize(Seq(
  Edge(5L, 7L, "friend"),
  Edge(5L, 1L, "friend"),
  Edge(1L, 2L, "friend"),
  Edge(2L, 3L, "friend"),
  Edge(6L, 9L, "friend"),
  Edge(9L, 8L, "friend")
))

//建立一個Graph圖
val graph = Graph(vertices, edges, null)

呼叫圖graph的connectedComponents函數，順便列印一下效果，可以看到，左邊子圖{(5L, "Eve"), (7L, "Grace"), (1L, "Alice"), (2L, "Bob"), (3L, "Charlie")}裡的各個頂點都關聯到了最小頂點1，右邊子圖{(8L, "Henry")，(9L, "Ivy")，(6L, "Frank")}裡的各個頂點都關聯到了最小頂點6。

val cc = graph.connectedComponents()
cc.vertices.foreach(println)

列印的結果——
(2,1)
(6,6)
(7,1)
(1,1)
(9,6)
(8,6)
(3,1)
(5,1)

注意一點，connectedComponents是可以傳參的，傳入的數位，是代表各個頂點最高可以連通迭代到多少步去尋找所在子圖裡的最小頂點。

舉個例子，可能就能明白了，假如，給connectedComponents傳參為1，那麼程式碼執行列印後，如下——

val cc = graph.connectedComponents(1)
cc.vertices.foreach(println)

列印的結果——
(2,1)
(5,1)
(8,8)
(7,5)
(1,1)
(9,6)
(6,6)
(3,2)

你會發現，各個頂點的連通元件即關聯所在子圖的最小頂點，大多都變了，這是因為設定引數為1 後，各個頂點沿著邊去迭代尋找連通元件時，只能迭代一步，相當本頂點只能走到一度鄰居頂點，然後將本頂點和鄰居頂點比較，誰最小，最小的當作連通元件。

以下圖說明，就是頂點(7L, "Grace")迭代一步去尋找最小頂點做連通元件，只能迭代到頂點(5L, "Eve")，沒法迭代到 (1L, "Alice")，這時頂點(7L, "Grace")就會拿自身與頂點(5L, "Eve")比較，發現5L更小，就會用5L當作自己的連通元件做關聯，即(7,5)。

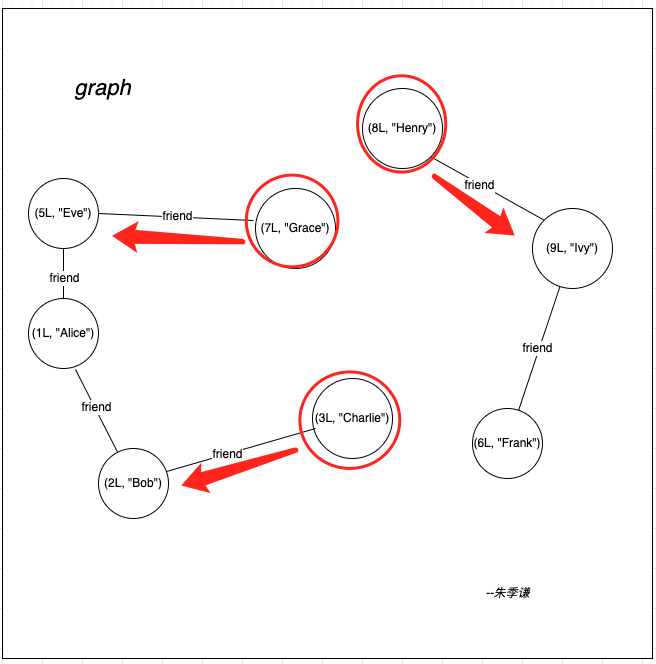
當然，實際底層的原始碼實現，並非是通過迭代多少步去尋找最小頂點，它的實現方式更精妙，站在原地就可以收集到所能迭代最大次數範圍內的最小頂點。

如果connectedComponents沒有設定引數，就會預設最大迭代次數是Int.MaxValue，2 的 31 次方 - 1即2147483647。

在實際業務當中，可以通過設定引數來避免在過大規模的子圖裡做耗時過長的迭代操作

接下來，就可以通過連通元件做分組，將具有共同連通元件的頂點分組到一塊，這樣就知道哪些頂點屬於同一子圖了。

val cc = graph.connectedComponents()
val group = cc.vertices.map{
  case (verticeId, minId) => (minId, verticeId)
}.groupByKey()

group.foreach(println)


列印結果——
(1,CompactBuffer(1, 2, 3, 5, 7))
(6,CompactBuffer(8, 9, 6))

基於這個函數，就可以得到哪些頂點在一張關係網裡了。

三、connectedComponents原始碼解析

先來看一下connectedComponents函數原始碼，在ConnectedComponents單例物件裡，可以看到，如果沒有傳參的話，預設迭代次數是Int.MaxValue，如果傳參的話，就使用引數的maxIterations做迭代次數——

/**
*無引數
*/
def connectedComponents(): Graph[VertexId, ED] = {
  ConnectedComponents.run(graph)
}


def run[VD: ClassTag, ED: ClassTag](graph: Graph[VD, ED]): Graph[VertexId, ED] = {
    run(graph, Int.MaxValue)
}



/**
*有引數
*/
def connectedComponents(maxIterations: Int): Graph[VertexId, ED] = {
    ConnectedComponents.run(graph, maxIterations)
}

在run方法裡，主要是做了一些函數和常數的準備工作，然後將這些函數和常數傳給單例物件Pregel的apply方法。apply是單例物件的特殊方法，就像Java類裡的構造方法一樣，建立物件時可以直接被呼叫。Pregel(ccGraph, initialMessage,maxIterations, EdgeDirection.Either)(......)最後呼叫的就是Pregel裡的apply方法。

def run[VD: ClassTag, ED: ClassTag](graph: Graph[VD, ED],
                                    maxIterations: Int): Graph[VertexId, ED] = {
  require(maxIterations > 0, s"Maximum of iterations must be greater than 0," +
    s" but got ${maxIterations}")
  //step1 初始化圖，將各頂點id設定為頂點屬性，圖頂點結構（vid,vid）
  val ccGraph = graph.mapVertices { case (vid, _) => vid }
  
  //step2 處理圖裡的每一個三元組邊物件，該物件edge包含了源頂點(srcId，srcAttr)和目標頂點(dstId，dstAttr)的資訊,及邊屬性attr，即（srcId，srcAttr，dstId，dstAttr，attr）
  def sendMessage(edge: EdgeTriplet[VertexId, ED]): Iterator[(VertexId, VertexId)] = {
    //如果源頂點屬性小於目標頂點屬性
    if (edge.srcAttr < edge.dstAttr) {
      //儲存（目標頂點id,源頂點屬性），這裡的源頂點屬性等於源頂點id,其實儲存的是（目標頂點id,源頂點id）
      Iterator((edge.dstId, edge.srcAttr))
       //如果源頂點屬性大於目標頂點屬性
    } else if (edge.srcAttr > edge.dstAttr) {
      //儲存（源頂點id,目標頂點id）
      Iterator((edge.srcId, edge.dstAttr))
    } else {
      //如果兩個頂點屬性相同，說明已經在同一個子網裡，不需要處理
      Iterator.empty
    }
  }
  //step3 設定一個初始最大值，用於在初始化階段，比較每個頂點的屬性，這樣頂點屬性值在最初階段就相當是最小頂點
  val initialMessage = Long.MaxValue
  
  //step4 將上面設定的常數和函數當作引數傳給Pregel，其中EdgeDirection.Either表示處理包括出度和入度的頂點。
  val pregelGraph = Pregel(ccGraph, initialMessage,
    maxIterations, EdgeDirection.Either)(
    //將最初頂點的屬性attr與initialMessage比較，相當是子圖的0次迭代尋找最小頂點
    vprog = (id, attr, msg) => math.min(attr, msg),
    //上面定義的sendMessage方法
    sendMsg = sendMessage,
    //處理各個頂點收到的訊息，然後將最小的頂點儲存
    mergeMsg = (a, b) => math.min(a, b))
  ccGraph.unpersist()
  pregelGraph
}

step1 初始化圖，將各頂點id設定為頂點屬性，圖頂點結構（vid,vid）——

 val ccGraph = graph.mapVertices { case (vid, _) => vid }

寫一個簡單的程式碼驗證一下即可知道得到的ccGraph處理後頂點是否為（vid，vid）結構了。

// 建立頂點RDD
val vertices = ss.sparkContext.parallelize(Seq(
  (1L, "Alice"),
  (2L, "Bob"),
  (3L, "Charlie"),
  (5L, "Eve"),
  (6L, "Frank"),
  (7L, "Grace"),
  (8L, "Henry"),
  (9L, "Ivy")
))

// 建立邊RDD
val edges = ss.sparkContext.parallelize(Seq(
  Edge(5L, 7L, "friend"),
  Edge(5L, 1L, "friend"),
  Edge(1L, 2L, "friend"),
  Edge(2L, 3L, "friend"),
  Edge(6L, 9L, "friend"),
  Edge(9L, 8L, "friend")
))

//建立一個Graph圖
val graph = Graph(vertices, edges, null)
graph.mapVertices{case  (vid,_) => vid}.vertices.foreach(println)

列印結果——
(2,2)
(5,5)
(3,3)
(6,6)
(7,7)
(8,8)
(1,1)
(9,9)

可見，ccGraph的圖頂點已經被處理成（vid,vid），即（頂點id, 頂點屬性），方便用於在sendMessage方法做屬性判斷處理。

step2 sendMessage處理圖裡的每一個三元組邊物件

前面處理的ccGraph頂點資料變成（頂點id, 頂點屬性）就是為了放在這裡做處理，這裡的if (edge.srcAttr < edge.dstAttr) 相當是if (edge.srcId < edge.dstId)。

這個方法是基於邊的三元組做處理，將同一邊的源頂點和目標頂點比較，篩選出兩個頂點最小的頂點，然後針對最大的頂點，保留（最大頂點，最小頂點屬性）這樣的資料。

  def sendMessage(edge: EdgeTriplet[VertexId, ED]): Iterator[(VertexId, VertexId)] = {
    //如果源頂點屬性小於目標頂點屬性
    if (edge.srcAttr < edge.dstAttr) {
      //儲存（目標頂點id,源頂點屬性），這裡的源頂點屬性等於源頂點id,其實儲存的是（目標頂點id,源頂點id）
      Iterator((edge.dstId, edge.srcAttr))
       //如果源頂點屬性大於目標頂點屬性
    } else if (edge.srcAttr > edge.dstAttr) {
      //儲存（源頂點id,目標頂點id）
      Iterator((edge.srcId, edge.dstAttr))
    } else {
      //如果兩個頂點屬性相同，說明已經在同一個子網裡，不需要處理
      Iterator.empty
    }
  }

這個方法的作用，就是找出同一條邊上哪個頂點最小，例如下圖中，2L比3L小，那麼2L是這條邊上最小的頂點，將以最大點關聯最小點的方式(edge.dstId, edge.srcAttr)即（3L，2L）儲存下來。最後會將（3L，2L）中的_.2也就是2L傳送給頂點（3L，3L），而頂點（3L，3L）後續需要做的事情是，是將這一輪收到的訊息即最小頂點2L與現在的屬性3L值通過math.min(a, b)做比較，保留最小頂點當作屬性值，即變成了（3L，2L）。

可見，在子圖裡，每一輪迭代後，各個頂點的屬性值都可能會被更新接收到的最小頂點值，這就是連通元件迭代的精妙。

這個方法會在後面的Pregel物件裡用到。

step3 設定一個初始最大值，用於比較後初始化每個頂點最初的屬性值

val initialMessage = Long.MaxValue需要與vprog = (id, attr, msg) => math.min(attr, msg)結合來看，相當在0次迭代時，將頂點（id，attr）的屬性值與initialMessage做比較，理論上，肯定是attr比較小，就意味著初始化時，頂點關聯的最小頂點就是attr，在這裡，就相當關聯的最小頂點是它本身，相當於子圖做了0次迭代處理。

step4 執行Pregel的建構函式apply方法

可以看到，前面建立的ccGraph，initialMessage，maxIterations（最大迭代次數），EdgeDirection.Either都當作引數傳給了Pregel。

val pregelGraph = Pregel(ccGraph, initialMessage,
    maxIterations, EdgeDirection.Either)(
    //將最初頂點的屬性attr與initialMessage比較，相當是子圖的0次迭代尋找最小頂點
    vprog = (id, attr, msg) => math.min(attr, msg),
    //上面定義的sendMessage方法
    sendMsg = sendMessage,
    //處理各個頂點收到的訊息，然後將最小的頂點儲存
    mergeMsg = (a, b) => math.min(a, b))

該Pregel物件底層主要就是對一系列的三元組邊的源頂點和目標頂點做比較，將兩頂點最小的頂點值傳送給該條邊最大的頂點，最大的頂點收到訊息後，會比較當前屬性與收到的最小頂點值比較，然後保留最小值。這樣，每一輪迭代，可能關聯的屬性值都會一直變化，不斷保留歷史最小頂點值，直到迭代完成。最後，就可以實現通過connectedComponents得到每個頂點都關聯到最小頂點的資料。

三、Pregel原始碼解析

Pregel是一個圖處理模型和計算框架，核心思想是將一系列頂點之間的訊息做傳遞和狀態更新操作，並以迭代的方式進行計算。讓我們繼續深入看一下它的底層實現。

以下是保留主要核心程式碼的函數——

def apply[VD: ClassTag, ED: ClassTag, A: ClassTag]
   (graph: Graph[VD, ED],
    initialMsg: A,
    maxIterations: Int = Int.MaxValue,
    activeDirection: EdgeDirection = EdgeDirection.Either)
   (vprog: (VertexId, VD, A) => VD,
    sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
    mergeMsg: (A, A) => A)
  : Graph[VD, ED] =
{
  ......
  //step1
  var g = graph.mapVertices((vid, vdata) => vprog(vid, vdata, initialMsg))
  ......
  //step2
  var messages = GraphXUtils.mapReduceTriplets(g, sendMsg, mergeMsg)
  ......
  //step3
  var activeMessages = messages.count()
  var prevG: Graph[VD, ED] = null
  var i = 0
  //step4
  while (activeMessages > 0 && i < maxIterations) {
    prevG = g
    g = g.joinVertices(messages)(vprog)
    val oldMessages = messages
    messages = GraphXUtils.mapReduceTriplets(
      g, sendMsg, mergeMsg, Some((oldMessages, activeDirection)))
    activeMessages = messages.count()
    i += 1
  }

  g
}

這行 var g = graph.mapVertices((vid, vdata) => vprog(vid, vdata, initialMsg))程式碼，需要聯絡到前面傳過來的引數，它的真實面目其實是這樣的——

var g = graph.mapVertices((vid, vdata) => {
  	(id, attr, initialMsg) => math.min(attr, initialMsg)
})

也就是前面step3裡提到的，這裡相當做了0次迭代，將attr當作頂點id關聯的最小頂點，初始化後，attr其實是頂點id本身。

var messages = GraphXUtils.mapReduceTriplets(g, sendMsg, mergeMsg)這行程式碼中，主要定義了一個函數sendMsg和呼叫了aggregateMessagesWithActiveSet方法。

private[graphx] def mapReduceTriplets[VD: ClassTag, ED: ClassTag, A: ClassTag](
    g: Graph[VD, ED],
    mapFunc: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
    reduceFunc: (A, A) => A,
    activeSetOpt: Option[(VertexRDD[_], EdgeDirection)] = None): VertexRDD[A] = {
  def sendMsg(ctx: EdgeContext[VD, ED, A]) {
    mapFunc(ctx.toEdgeTriplet).foreach { kv =>
      val id = kv._1
      val msg = kv._2
      if (id == ctx.srcId) {
        ctx.sendToSrc(msg)
      } else {
        assert(id == ctx.dstId)
        ctx.sendToDst(msg)
      }
    }
  }
  g.aggregateMessagesWithActiveSet(
    sendMsg, reduceFunc, TripletFields.All, activeSetOpt)
}

函數sendMsg裡需要看懂一點是，這裡的mapFunc(ctx.toEdgeTriplet)正是呼叫了前面定義的ConnectedComponents裡的sendMessage方法，因此，這個方法恢復原樣，是這樣的——

    def sendMsg(ctx: EdgeContext[VD, ED, A]) {
      (ctx.toEdgeTriplet => {
        case edge =>
        if (edge.srcAttr < edge.dstAttr) {
          Iterator((edge.dstId, edge.srcAttr))
        } else if (edge.srcAttr > edge.dstAttr) {
          Iterator((edge.srcId, edge.dstAttr))
        } else {
          Iterator.empty
        }
      }).foreach { kv =>
        val id = kv._1
        val msg = kv._2
        if (id == ctx.srcId) {
          ctx.sendToSrc(msg)
        } else {
          assert(id == ctx.dstId)
          ctx.sendToDst(msg)
        }
      }
    }

這個方法的作用，就是找出同一條邊上哪個頂點最小，例如下圖中，2L比3L小，那麼2L是這條邊上最小的頂點，將以最大點關聯最小點的方式(edge.dstId, edge.srcAttr)即（3L，2L）儲存下來。最後會將（3L，2L）中的_.2也就是2L傳送給頂點（3L，3L），而頂點（3L，3L）後續需要做的事情是，是將這一輪收到的訊息即最小頂點2L與現在的屬性3L值通過math.min(a, b)做比較，保留最小頂點當作屬性值，即變成了（3L，2L）。

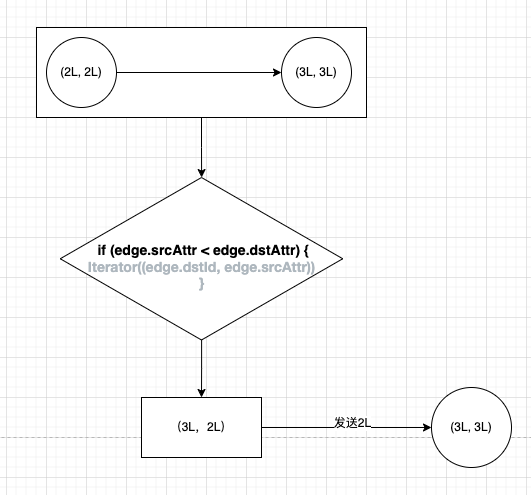
剩下aggregateMessagesWithActiveSet就是做聚合了，sendMsg就是上面的獲取最小頂點後傳送給頂點的操作，reduceFunc對應的是 mergeMsg = (a, b) => math.min(a, b))，保留歷史最小頂點當作該頂點屬性。

g.aggregateMessagesWithActiveSet(
  sendMsg, reduceFunc, TripletFields.All, activeSetOpt)

最後這個while遍歷，如果設定了迭代次數，迭代次數就會傳至給maxIterations，activeMessages表示還有多少頂點需要處理。

  while (activeMessages > 0 && i < maxIterations) {
    prevG = g
    g = g.joinVertices(messages)(vprog)
    val oldMessages = messages
    messages = GraphXUtils.mapReduceTriplets(
      g, sendMsg, mergeMsg, Some((oldMessages, activeDirection)))
    activeMessages = messages.count()
    i += 1
  }

這個方法，就是不斷做迭代，不斷更新各個頂點屬性對應的最小頂點，直到迭代出子圖裡的最小頂點。

很精妙的一點設計是，每個頂點只需要不斷迭代，以三元組邊為維度，互相將最小頂點傳送給屬性值（頂點保留的上一輪最小頂點所做的屬性）較大的頂點，頂點只需要保留收到的訊息裡最小的頂點更新為屬性值即可。