全域性多項式(趨勢面)與IDW逆距離加權插值:MATLAB程式碼
本文介紹基於MATLAB實現全域性多項式插值法與逆距離加權法的空間插值的方法,並對不同插值方法結果加以對比分析。
趁熱打鐵,前期我們完成了地學計算基本理論講解(見文章地統計學的基本概念及公式詳解)與空間資料變異函數計算與經驗半方差圖繪製(見文章MATLAB計算變異函數並繪製經驗半方差圖)這一地學計算的基本實踐操作後,我們將深入探討、實戰地學計算中插值問題的兩個重要方法:全域性多項式插值法與逆距離加權法。
為方便大家理解,本文將講解與程式碼部分獨立開來;首先將具體的操作流程與方法仔細闡述,其次將本文所用到的全部程式碼完整附於本文末尾。其中,由於本文所用的資料並不是我的,因此遺憾不能將資料一併提供給大家;但是依據本篇部落格的思想與對程式碼的詳細解釋,大家用自己手頭的資料,可以將相關操作與分析過程加以完整重現。
1 背景知識
空間資料的獲取是進行空間分析的基礎與起源,我們總是希望能夠獲取研究區域更多、更全面的精確空間屬性資料資訊。但在實際工作中,由於成本、資源等條件限制,不可能對全部未知區域加以測量,而更多隻能得到有限數量的取樣點的資料。因此,可以考慮選取合適的空間取樣點,利用一定數學模型,依據已知取樣點資料對研究區域所有位置的未知屬性資訊加以預測。
空間插值(Spatial Interpolation)即是一種將離散點測量資料轉換為連續資料曲面的常用方法,包括內插(Interpolation)和外推(Extrapolation)兩種應用形式。空間插值基於地理學第一定律,即一般地,距離越近的地物具有越高的相關性。
在方法層面,空間插值一般可以分為確定性插值方法(Deterministic Interpolation)與地質統計學方法(Geostatistics)。前者基於資訊點之間相似程度或整個曲面的平滑程度建立擬合曲面,後者則基於資訊點綜合統計學規律,對其空間自相關性定量化,從而建立插值面。另一方面,依據插值計算時納入考慮的取樣點分佈範圍,又分為整體插值法與區域性插值法。前者利用整個實測取樣點資料集對全區進行擬合,如全域性多項式插值法(Global Polynomial Interpolation);後者則只是用臨近某一區域內的取樣點資料預測未知點的資料,如反(逆)距離加權法(Inverse Distance Weighted,IDW)。此外,依據插值結果曲面中取樣點預測值與實測值的關係,又可分為精確性插值與不精確插值。
本文藉助MATLAB軟體自主程式設計,分別利用全域性多項式插值法與逆距離加權法,對湖北省荊門市沙洋縣土壤pH值、有機質含量等兩種屬性資料進行空間插值計算,並對比對應插值方法的擬合效果。
全域性多項式插值法以全部取樣點覆蓋區域為基礎,通過最小二乘法等手段擬合出一個最合適的平面或曲面,使得各個取樣點較為均勻地分佈於這一平面或曲面的附近,且全部高出該面的點距之和與全部低於該面的點距之和的絕對值應當近似。全域性多項式插值法不適合描述屬性資料空間分佈波動較大區域的特徵。
逆距離加權法則利用待插值點周圍一定範圍的已知點資料,對中心待插點加以資料插值;某點距離待插點越近,其對這一點的影響越大,即對應係數越大。而權重的計算往往依賴於反距離(距離倒數)的p次方。一般地,取p等於2。依據方法原理可知,逆距離加權法往往會導致空間分佈的多點中心現象。
2 實際操作部分
2.1 空間資料讀取
本文利用上述MATLAB計算變異函數並繪製經驗半方差圖中的資料為範例,其包括湖北省荊門市沙洋縣658個土壤取樣點的空間位置(X與Y,單位為米)、pH值、有機質含量與全氮含量。這些資料同樣儲存於data.xls檔案中,而後期操作多基於MATLAB軟體加以實現。因此,首先需根據具體計算需要將源資料選擇性地匯入MATLAB軟體中。
2.2 異常資料剔除
同上述部落格所述,我們得到的原始取樣點資料在取樣記錄、實驗室測試等過程中,可能具有一定誤差,從而出現個別異常值;而異常值的存在會對後期空間插值效果(尤其是區域性插值方法)產生較大影響。因此,選用平均值加標準差法對異常資料加以篩選、剔除。這一方法的具體含義請見MATLAB計算變異函數並繪製經驗半方差圖。
上述部落格中,分別利用「2S」與「3S」方法加以處理,發現「2S」方法處理效果相對後者較好。故本文直接選擇使用「2S」方法處理結果繼續進行。
得到異常值後,將其從原有658個取樣點中剔除;剩餘的取樣點資料繼續後續操作。
2.3 驗證集篩選
針對不同插值方法所得結果的精度檢驗,本文采取設定訓練資料(Training Data)與測試資料(Test Data)並對比的方式進行。將經過上述異常剔除後的資料隨機分為兩個部分,其中80%作為訓練資料,剩餘20%作為測試資料(即驗證集)。需要注意的是,測試資料僅可用於檢測插值模型的構建效果,而不可參與模型構建過程,否則可能導致結果過度擬合(即模型對本次所給資料具有較好插值、擬合效果,但對外圍無資料區域的預測效果較差)。由於驗證集資料為隨機選取,因此後期可多次執行程式,以期獲得平穩的精度衡量指標。
2.4 最小二乘法求解
正如全域性多項式插值法名稱所示,這一插值方法的原理實際上是對一個描述平面或曲面的多項式各個係數加以求解;而這一求解過程往往採用最小二乘法實現。
考慮到多項式的複雜度,本文將多項式階數限定為二階與三階,並對其插值效果加以對比。二階多項式形式如下:
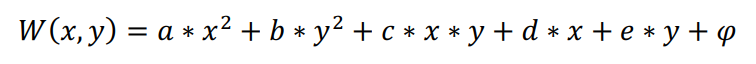
三階多項式形式如下:
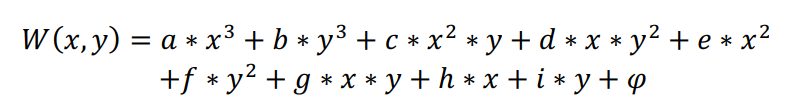
上述兩公式中,W(x,y)為待插點(x,y)的插值,x與y為座標,φ為常數,其它字母代表各對應項係數。
若利用AcrMap等軟體進行趨勢面插值,則可依據實際情況適當提升階數。
2.5 逆距離加權法求解
逆距離加權法通過各已知點自身實際數值及其關於待插點的權重實現插值,公式如下:
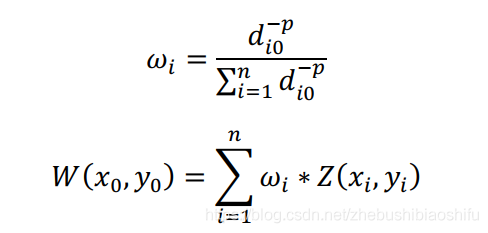
其中,ω_i為第i個已知點對待插點(x_0,y_0 )的權重,d_i0為二者間距離,n為已知點個數,p為冪引數,W(x_0,y_0 )為待插點(x_0,y_0 )的插值,Z(x_i,y_i )為第i個已知點對應屬性數值。
本文中,取初始p=2,並依據插值效果適當對其加以調整。
2.6 插值精度檢驗
如前所述,本文通過隨機選定的測試資料對插值結果的精度進行比較與分析。結合實際空間資料的數值特點,最終所選用以衡量插值精度的指標包括平均誤差(Mean Error,ME)[1]、平均絕對誤差(Mean Absolute Error,MAE)、均方根誤差(Root Mean Square Error,RMSE)與相關係數(Correlation Coefficient)。
其中,平均誤差可以獲知插值結果與實測點觀測值的大小關係;平均絕對誤差表示空間插值與實測點觀測值之間絕對誤差的平均值,可以更好反映插值結果誤差的實際情況;均方根誤差表示插值結果與實測點觀測值之間差異(即殘差)的樣本標準差;相關係數(這裡選用皮爾遜相關係數)用以評價空間插值與實測點觀測值之間的線性相關度。
2.7 資料匯出與專題地圖製作
通過上述過程,得到對應屬性資料的插值結果。首先在MATLAB繪製插值結果三維圖,隨後將插值結果資料變數儲存為ASCII資料格式檔案,並匯入AcrMap軟體繪製專題地圖。
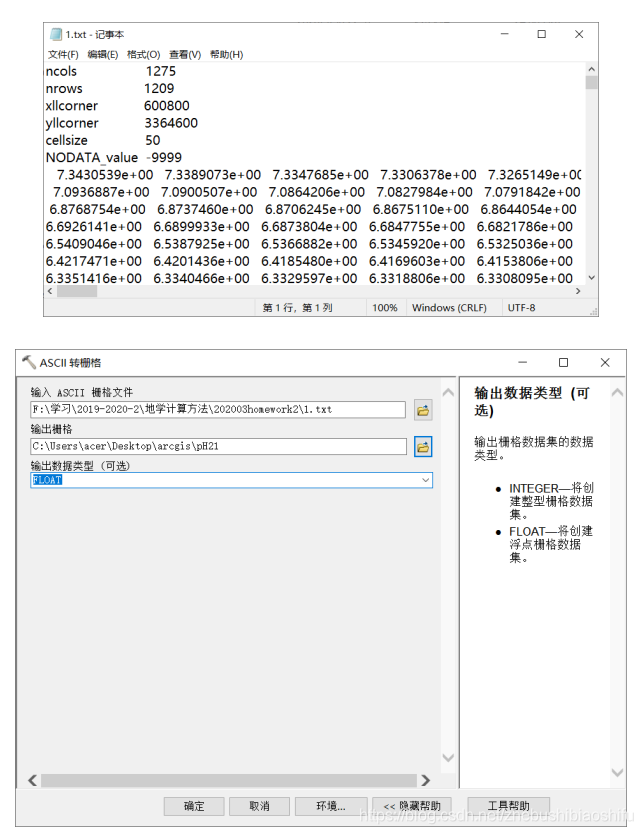
其中,在資料由MATLAB匯出為.txt格式後,需要在其開頭部分新增以下資訊:
ncols 1275
nrows 1209
xllcorner 600800
yllcorner 3364600
cellsize 50
NODATA_value -9999
其中,ncols與nrows對應數值分別代表插值結果列數與行數,xllcorner與yllcorner對應數值分別代表插值結果x、y座標的最小值(即起始值),cellsize對應數值代表像元大小。
3 結果呈現與分析
通過平均誤差、平均絕對誤差、均方根誤差、相關係數等四個精度衡量指標,以及對應趨勢面公式與三維插值結果圖,將不同空間插值方法所得結果對比、分析如下,並繪製專題地圖。
3.1 全域性多項式插值法二階與三階插值對比
利用最小二乘法,分別對二階多項式與三階多項式進行係數求解,並得到pH值、有機質含量等兩種空間屬性資料的全域性多項式插值結果與各精度指標。針對不同階數多項式,分別執行六次插值操作,並求出平均值。得到結果分別如表1至表6所示。
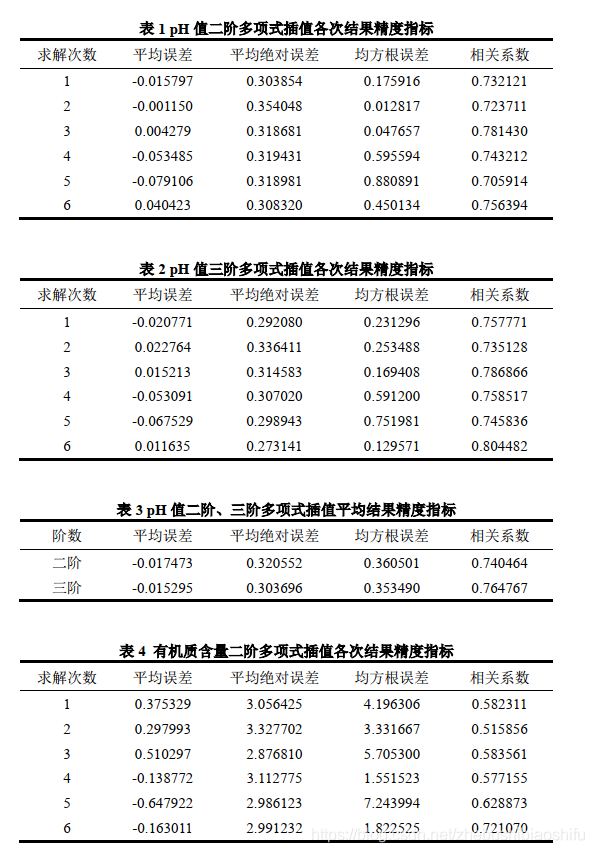
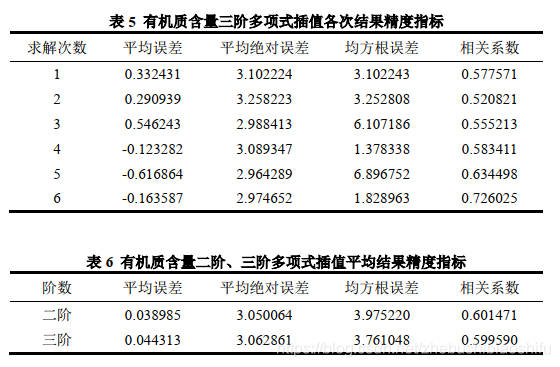
由表1至表3可知,針對pH值的全域性多項式插值法,二階、三階多項式所得插值結果的平均誤差均為負數,即兩種方法均趨向於獲得較之觀測值高的插值結果;而後者所得平均誤差的數值較小於前者(即後者這一指標絕對值較小)。二階、三階多項式插值結果對應平均絕對誤差、均方根誤差相差不大,但後者上述兩種指標數值同樣小於前者。三階多項式相關係數同樣略大於二階多項式。綜上所述,面向pH值的全域性多項式插值法,其運用三階多項式的插值效果較優於運用二階多項式的插值效果,且這一結果在平均誤差、平均絕對誤差、均方根誤差與相關係數等四個精度衡量指標中均有所體現。
由表4至表6可知,針對有機質含量的全域性多項式插值法,二階、三階多項式所得插值結果的平均誤差均為正數,即兩種方法均趨向於獲得較之觀測值低的插值結果;而後者所得平均誤差的數值較大於前者。二階、三階多項式插值結果對應平均絕對誤差相差不大,但後者上述指標數值同樣略大於前者。二階多項式的均方根誤差較之三階多項式低,且二者這一指標有著較為明顯的差距。三階多項式相關係數同樣略小於二階多項式。綜上所述,面向有機質含量的全域性多項式插值法,其運用二階多項式的插值效果與運用三階多項式的插值效果整體區分度不大,二階多項式插值結果在平均誤差、平均絕對誤差與相關係數等三個精度衡量指標中略優於三階多項式,而三階多項式插值結果則在均方根誤差這一指標中表現出色。考慮到不同測試資料的選取具有隨機性,因此認為上述較為接近的結果並不能特別表現出二者中更優的插值方法選擇。
綜合表1至表6可知,對於全域性多項式插值法,其多項式階數的選擇並不一定是越高越好,而是需要依據實際資料情況加以嘗試、選擇。較高的階數除了會增大計算量、延長程式執行時間外,其插值結果精度亦有可能並無增長,甚至在某些指標中出現下降趨勢。
3.2 全域性多項式插值法函數及其三維結果圖
綜上所述,分別利用二階多項式與三階多項式獲取全域性多項式插值法對應趨勢面函數。
針對pH值的二階、三階全域性多項式插值趨勢面函數如下:
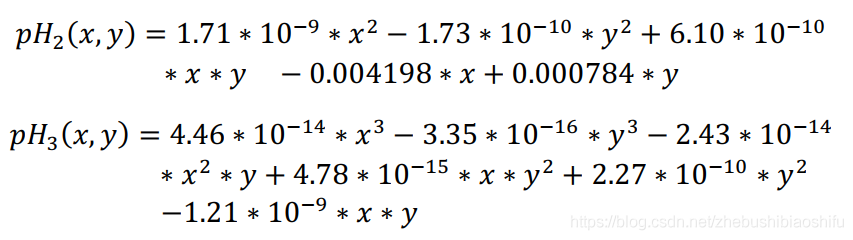
其中,上述二階與三階趨勢面函數分別對應各精度衡量指標情況如表7所示。

上述二階與三階趨勢面函數分別對應三維插值結果圖如下。
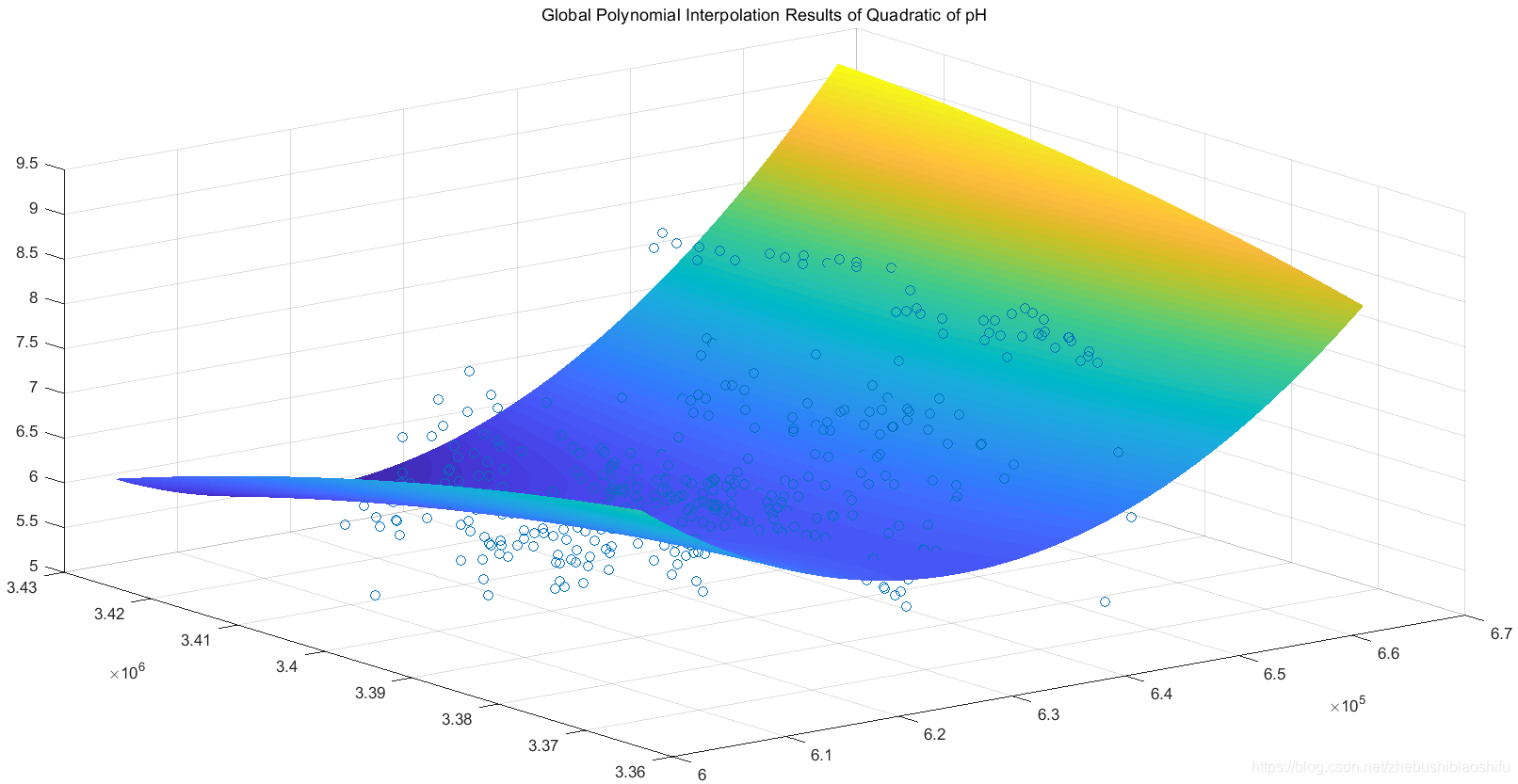
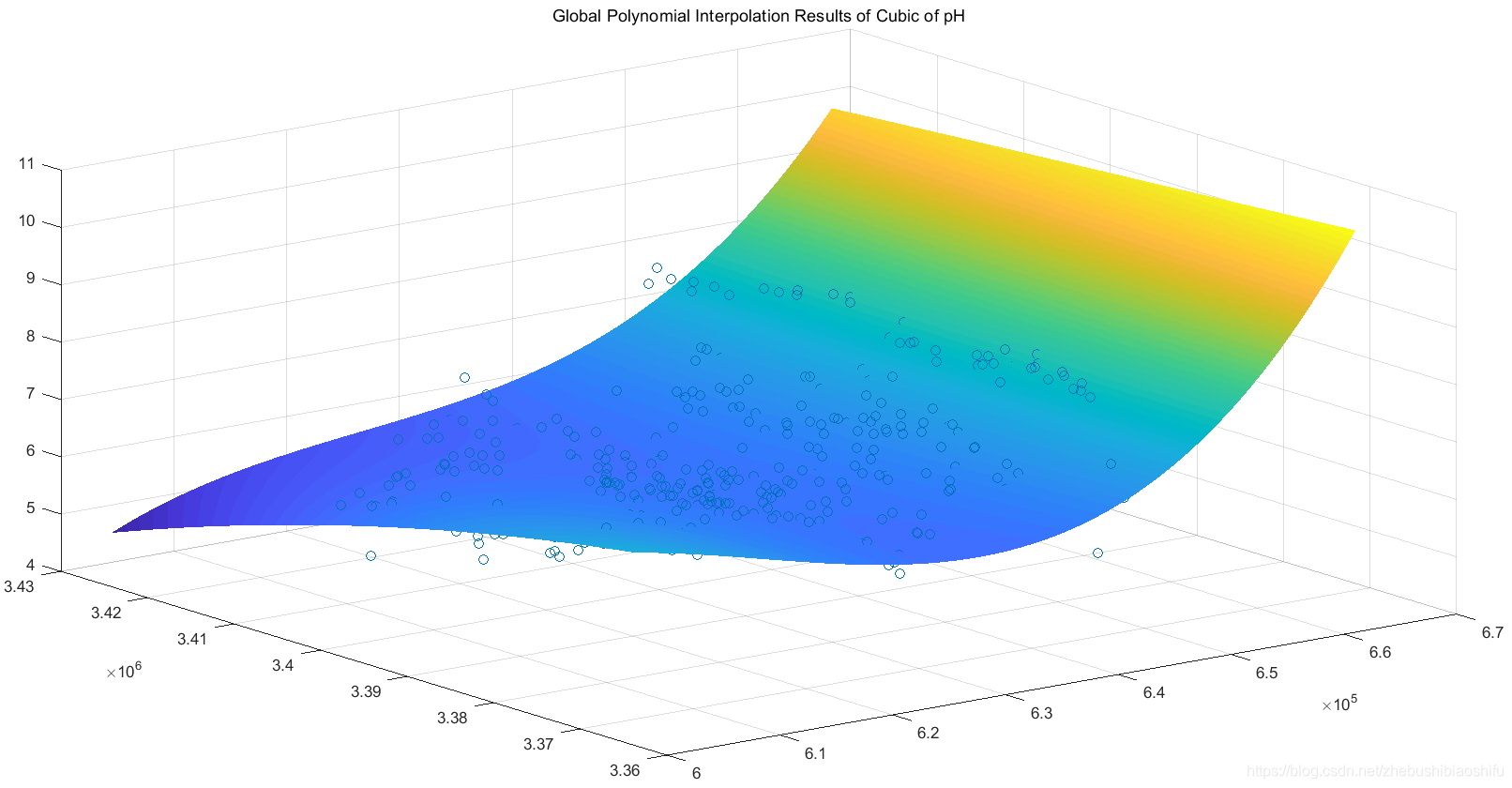
針對有機質含量的二階、三階全域性多項式插值趨勢面函數如下:

其中,上述二階與三階趨勢面函數分別對應各精度衡量指標情況如表8所示。
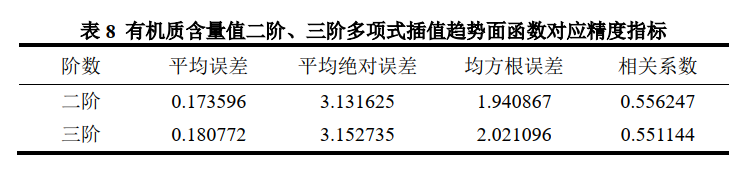
上述二階與三階趨勢面函數分別對應三維插值結果圖如下。
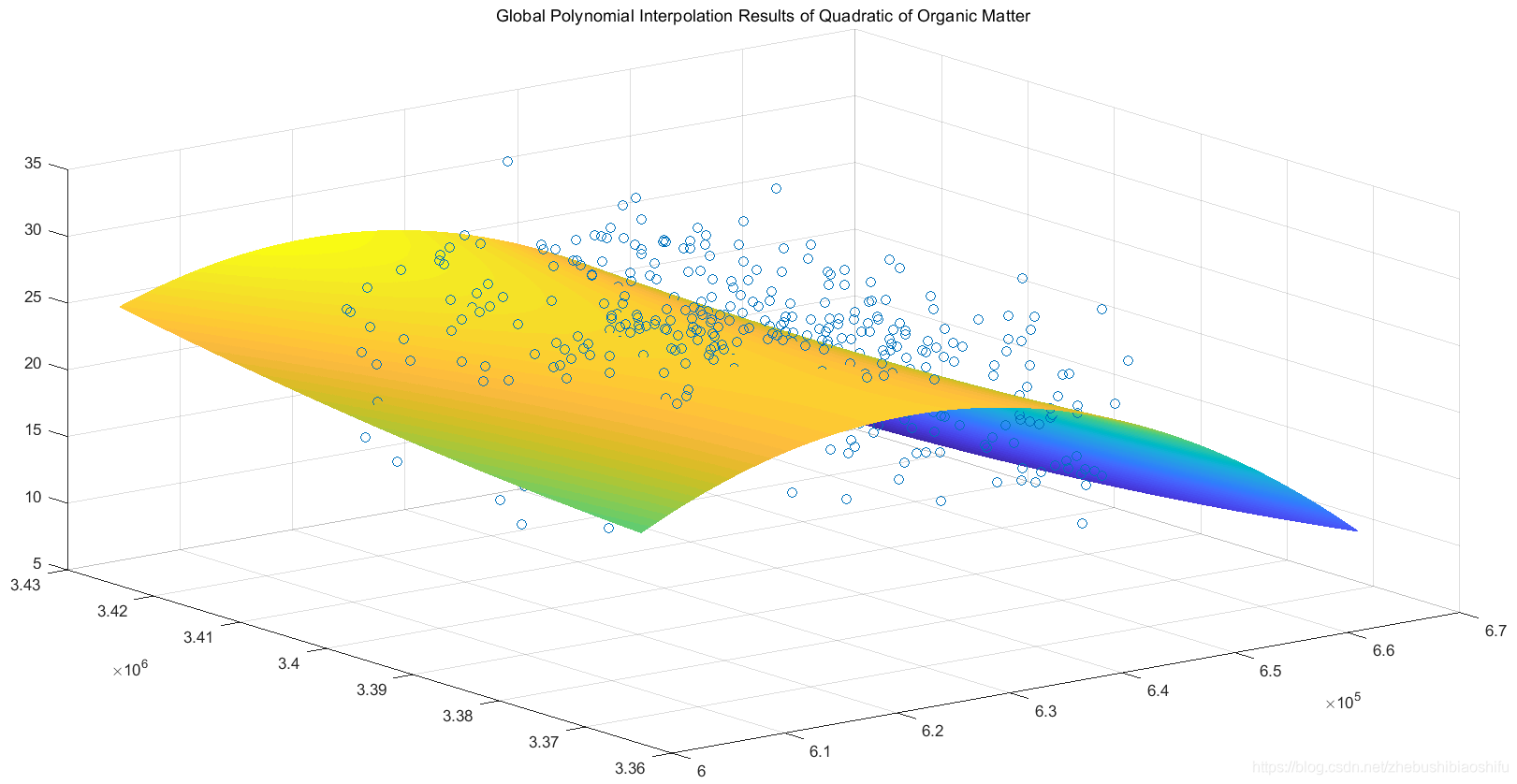
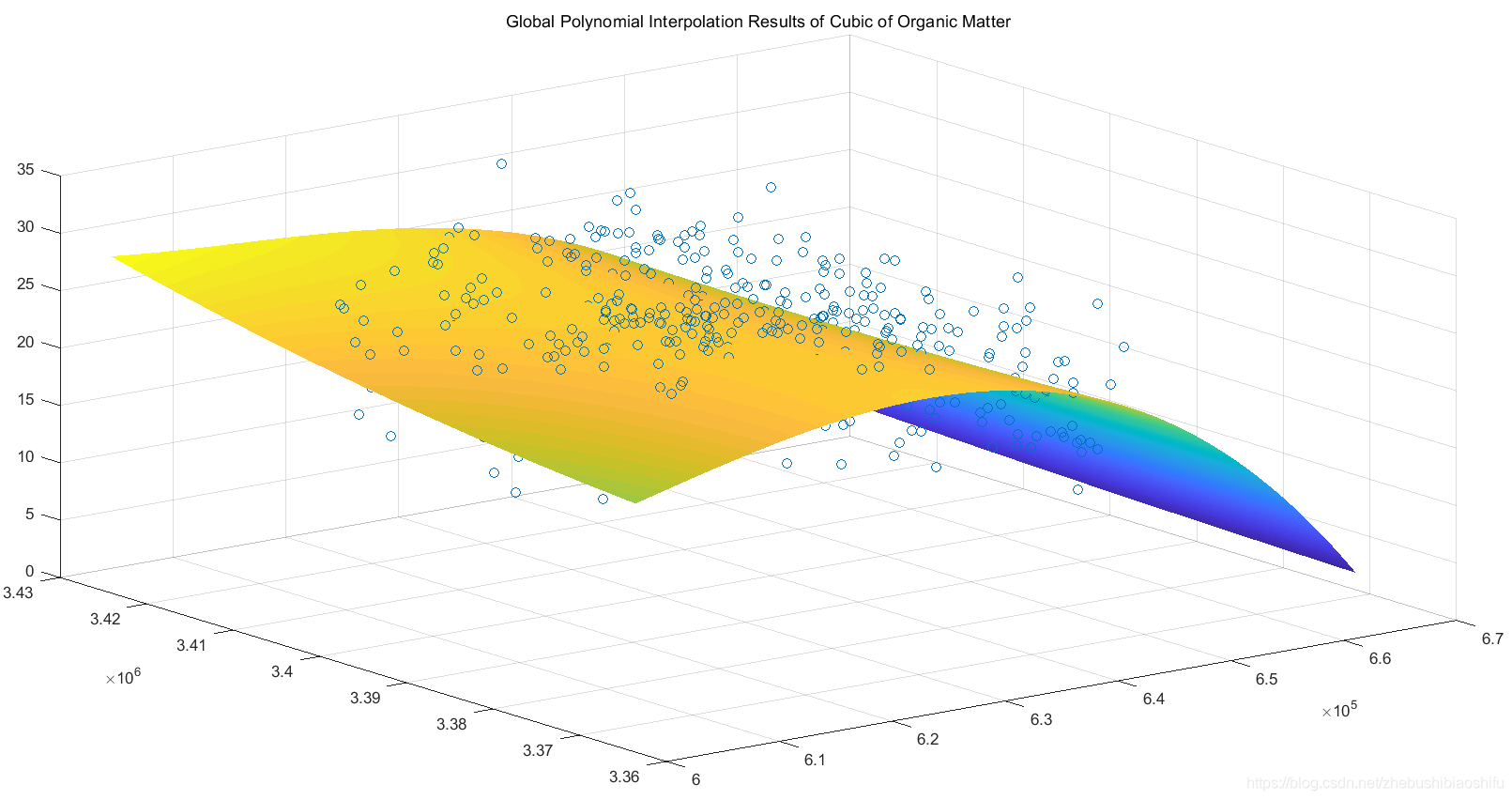
3.3 全域性多項式插值法專題地圖繪製
通過本文前述部分的相關方法,將MATLAB插值資料結果檔案匯入ArcMap,經過剪裁後製作湖北省荊門市沙洋縣土壤pH值、有機質含量全域性多項式插值專題地圖。其中,專題地圖的具體制作方法這裡就不再贅述了,大家可以參考ENVI大氣校正方法反演Landsat 7地表溫度中的方法。
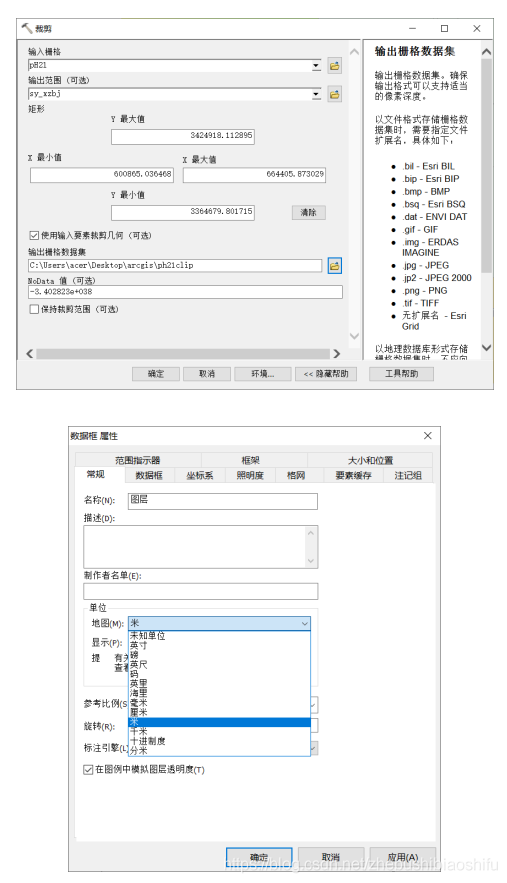
得到專題地圖如下所示。
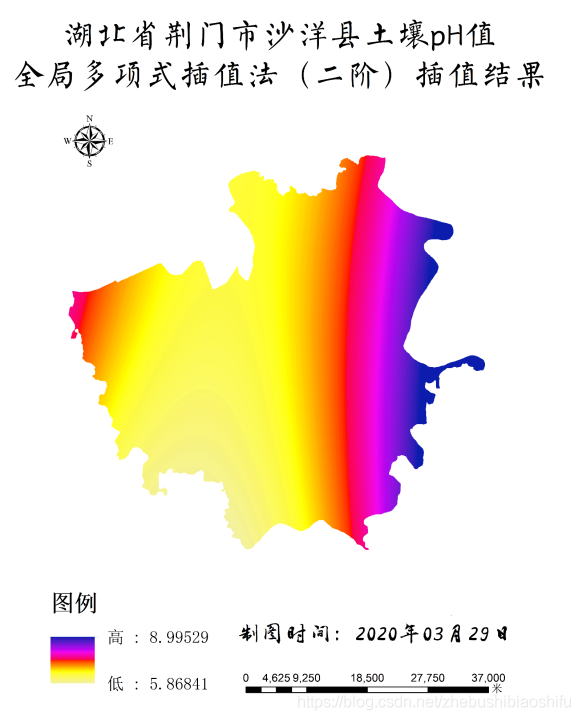
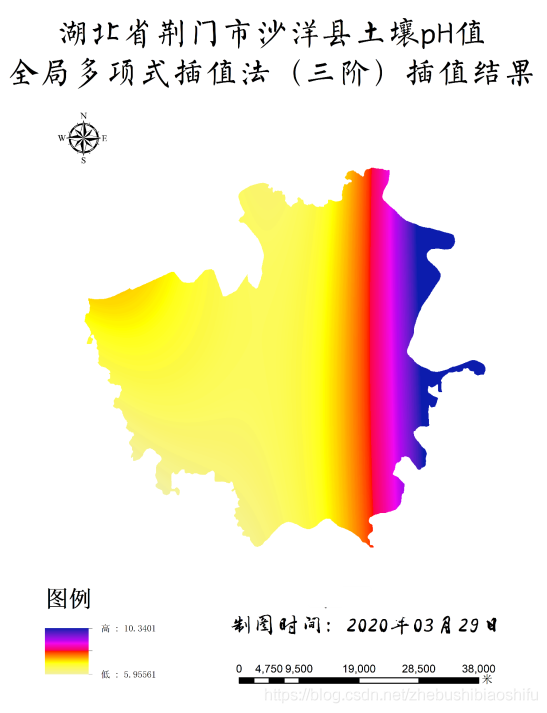


由上述四幅專題地圖可知,三階多項式插值所得結果較之二階多項式普遍具有更廣的數值範圍,如二階pH值插值地圖中最大結果為8.99,而其三階插值則可達到10.34;同樣,二階有機質含量插值地圖中最小結果為8.91,而其三階插值則可低至5.53。針對這一現象,個人認為可能是由於三階多項式插值曲面彎曲程度較之二階多項式插值更大,平滑效應較之二階多項式不明顯,因此其所能達到的數值範圍亦較大。
另一方面,由專題地圖這一角度觀之,可以發現pH值與有機質含量分佈具有一定空間關係:pH值較高區域,有機質含量往往較低(主要集中於沙洋縣東部地區);反之,有機質含量則往往較高(主要集中於沙洋縣中、西部地區)。而這一結果也符合「土壤有機質與pH值之間具有較高負相關關係」的結論[2]。
3.4 逆距離加權法插值結果及其三維結果圖
依據本文前述方法,取初始p=2,並依據插值效果適當調整,多次重複執行逆距離加權法,得到pH值、有機質含量等兩種空間屬性資料的插值結果與各精度指標。得到結果如表9所示。

由表9可知,面向pH值與有機質含量的逆距離加權法插值效果在上述四個精度衡量指標中表現並不是特別理想,較之前述全域性多項式插值法(包括二階、三階)結果誤差略大。尤其是有機質含量逆距離加權法結果的均方根誤差,其平均數值已達5.10左右,說明各次IDW方法的有機質含量插值結果與實測點觀測值之間差異(即殘差)的樣本標準差較大。此外,逆距離加權法有機質含量插值結果的平均相關係數未高於0.50。而與有機質含量相比,pH值的插值結果各項精度衡量指標整體稍優;由此可以看出,pH值的逆距離加權法插值效果整體精度較好於有機質含量;而這可能與兩種屬性資料各自內部的空間相關性、數值取值、分佈特徵等有關。由整體精度衡量指標來看,程式設計實現的逆距離加權法效果較之全域性多項式插值法略差。
另一方面,在多次執行逆距離加權法插值過程中發現,每次執行效果精度差異變化較大;尤其是有機質含量,有時上述各項精度指標可以達到一個很好的水平,而有時則較差,如均方根誤差甚至有時可達8左右。由此抑或可以看出,逆距離加權法作為一種區域性插值方法,其執行效果所受到訓練資料與測試資料的選取情況影響較大。
pH值與有機質含量的逆距離加權法插值三維結果分別如下兩幅圖所示。


3.5 逆距離加權法專題地圖繪製
通過本文前述部分的相關方法,將MATLAB插值資料結果檔案匯入ArcMap,經過剪裁後製作湖北省荊門市沙洋縣土壤pH值、有機質含量逆距離加權法插值專題地圖。
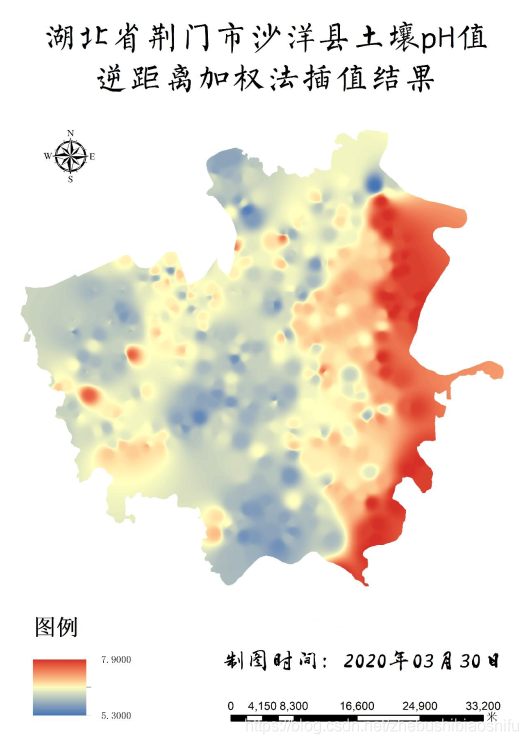

由上述兩幅專題地圖可知,逆距離加權法插值所得結果較之全域性多項式插值法,生成的表面起伏變化數量更多、程度更大,而起伏所影響的範圍則較小;且如前所述,逆距離加權法得到的插值結果具有較多小範圍的中心分佈區域,即插值專題圖中可見包含若干氣泡狀小點分佈的屬性資料特徵。此外,pH值與有機質含量的分佈特徵及其二者間的空間相互關係依然同全域性多項式插值法結果,即二者資料大小間呈現出相反狀態,沙洋縣中、西部地區pH值相對較低而有機質含量較高,東部地區則pH值相對較高而有機質含量較低。
同時,正如本文第一部分所述,由於逆距離加權法是一種區域性插值法,每一待插點的插值結果均很大程度上受到其臨近點數值的影響;因此上述空間分佈特徵亦只是其結果的整體趨勢,其中也會有部分特例。例如,結合上述兩幅專題地圖可以看到,逆距離加權法所得pH值插值結果在沙洋縣西部地區亦有部分區域性極大值點,而這些極大值點的數值甚至與東部地區持平;同時,其有機質含量插值結果在沙洋縣中、西部地區亦存在零星散佈的區域性極小值點。
4 完整程式碼
4.1 全域性多項式插值法MATLAB程式碼
%% 檔案資訊讀入
clc;clear;
info=xlsread('data.xls');
opoX=info(:,1);
opoY=info(:,2);
oPH=info(:,3);
% oOM=info(:,4);
% oTN=info(:,5);
%% 2S法計算異常值
mPH=mean(oPH);
sPH=std(oPH);
num2=find(oPH>(mPH+2*sPH)|oPH<(mPH-2*sPH));
%% 異常值剔除
PH=oPH;
for i=1:length(num2)
n=num2(i,1);
PH(n,:)=[0];
end
PH(all(PH==0,2),:)=[];
poX=opoX;
for i=1:length(num2)
n=num2(i,1);
poX(n,:)=[0];
end
poX(all(poX==0,2),:)=[];
poY=opoY;
for i=1:length(num2)
n=num2(i,1);
poY(n,:)=[0];
end
poY(all(poY==0,2),:)=[];
%% 驗證集篩選
very=[randperm(length(PH),floor(length(PH)*0.2))]';
%% 驗證集剔除
cPH=PH;
vPH=zeros(length(very),1);
vpoX=vPH;
vpoY=vPH;
for i=1:length(very)
m=very(i,1);
vPH(i,:)=cPH(m,:);
cPH(m,:)=[0];
end
cPH(all(cPH==0,2),:)=[];
cpoX=poX;
for i=1:length(very)
m=very(i,1);
vpoX(i,:)=cpoX(m,:);
cpoX(m,:)=[0];
end
cpoX(all(cpoX==0,2),:)=[];
cpoY=poY;
for i=1:length(very)
m=very(i,1);
vpoY(i,:)=cpoY(m,:);
cpoY(m,:)=[0];
end
cpoY(all(cpoY==0,2),:)=[];
%% 最小二乘法求解預處理
inva2=[ones(size(cpoX)),cpoX.^2,cpoY.^2,cpoX.*cpoY,cpoX,cpoY];
inva3=[ones(size(cpoX)),cpoX.^3,cpoY.^3,(cpoX.^2).*cpoY,cpoX.*(cpoY.^2),cpoX.^2,cpoY.^2,cpoX.*cpoY,cpoX,cpoY];
%% 最小二乘法求解
[coef2,bint2,r2,rint2,stats2]=regress(cPH,inva2);
[coef3,bint3,r3,rint3,stats3]=regress(cPH,inva3);
%% 趨勢面法效果圖繪製準備
step=50;
npoX=600800:step:664500;
npoY=3364600:step:3425000;
[mnpX,mnpY]=meshgrid(npoX,npoY);
%% 趨勢面法插值
pPH2=coef2(1,:)+coef2(2,:)*mnpX.^2+coef2(3,:)*mnpY.^2+coef2(4,:)*mnpX.*mnpY+coef2(5,:)*mnpX+coef2(6,:)*mnpY;
pPH3=coef3(1,:)+coef3(2,:)*mnpX.^3+coef3(3,:)*mnpY.^3+coef3(4,:)*(mnpX.^2).*mnpY+coef3(5,:)*mnpX.*(mnpY.^2)+coef3(6,:)*mnpX.^2+coef3(7,:)*mnpY.^2+coef3(8,:)*mnpX.*mnpY+coef3(9,:)*mnpX+coef3(10,:)*mnpY;
%% 趨勢面法效果圖繪製
scatter3(cpoX,cpoY,cPH);
hold on;
mesh(mnpX,mnpY,pPH2);
title('Global Polynomial Interpolation Results of Quadratic of Organic Matter');
figure();
scatter3(cpoX,cpoY,cPH);
hold on;
mesh(mnpX,mnpY,pPH3);
title('Global Polynomial Interpolation Results of Cubic of Organic Matter');
%% 趨勢面法精度對比
vpPH2=coef2(1,:)+coef2(2,:)*vpoX.^2+coef2(3,:)*vpoY.^2+coef2(4,:)*vpoX.*vpoY+coef2(5,:)*vpoX+coef2(6,:)*vpoY;
MEERan2=mean(vPH-vpPH2);
MEERan21=mean(abs(vpPH2-vPH));
RMSEan2=sqrt(sum(vpPH2-vPH).^2/length(vPH));
COCOan2=corrcoef(vpPH2,vPH);
vpPH3=coef3(1,:)+coef3(2,:)*vpoX.^3+coef3(3,:)*vpoY.^3+coef3(4,:)*(vpoX.^2).*vpoY+coef3(5,:)*vpoX.*(vpoY.^2)+coef3(6,:)*vpoX.^2+coef3(7,:)*vpoY.^2+coef3(8,:)*vpoX.*vpoY+coef3(9,:)*vpoX+coef3(10,:)*vpoY;
MEERan3=mean(vPH-vpPH3);
MEERan31=mean(abs(vpPH3-vPH));
RMSEan3=sqrt(sum(vpPH3-vPH).^2/length(vPH));
COCOan3=corrcoef(vpPH3,vPH);
%% 趨勢面法匯出ASCII
save 3.txt pPH2 -ASCII;
save 4.txt pPH3 -ASCII;
4.2 逆距離加權法MATLAB程式碼
%% 檔案資訊讀入
clc;clear;
info=xlsread('data.xls');
opoX=info(:,1);
opoY=info(:,2);
oPH=info(:,3);
power=2;
% oOM=info(:,4);
% oTN=info(:,5);
%% 2S法計算異常值
mPH=mean(oPH);
sPH=std(oPH);
num2=find(oPH>(mPH+2*sPH)|oPH<(mPH-2*sPH));
%% 異常值剔除
PH=oPH;
for i=1:length(num2)
n=num2(i,1);
PH(n,:)=[0];
end
PH(all(PH==0,2),:)=[];
poX=opoX;
for i=1:length(num2)
n=num2(i,1);
poX(n,:)=[0];
end
poX(all(poX==0,2),:)=[];
poY=opoY;
for i=1:length(num2)
n=num2(i,1);
poY(n,:)=[0];
end
poY(all(poY==0,2),:)=[];
%% 驗證集篩選
very=[randperm(length(PH),floor(length(PH)*0.2))]';
%% 驗證集剔除
cPH=PH;
vPH=zeros(length(very),1);
vpoX=vPH;
vpoY=vPH;
for i=1:length(very)
m=very(i,1);
vPH(i,:)=cPH(m,:);
cPH(m,:)=[0];
end
cPH(all(cPH==0,2),:)=[];
cpoX=poX;
for i=1:length(very)
m=very(i,1);
vpoX(i,:)=cpoX(m,:);
cpoX(m,:)=[0];
end
cpoX(all(cpoX==0,2),:)=[];
cpoY=poY;
for i=1:length(very)
m=very(i,1);
vpoY(i,:)=cpoY(m,:);
cpoY(m,:)=[0];
end
cpoY(all(cpoY==0,2),:)=[];
%% IDW效果圖繪製準備
step=50;
npoX=600800:step:664500;
npoY=3364600:step:3425000;
[mnpX,mnpY]=meshgrid(npoX,npoY);
%% IDW分母計算
temdeno=zeros(1,length(cPH));
deno=zeros(length(npoY),length(npoX));
for p=1:length(npoY)
for q=1:length(npoX)
for i=1:length(cPH)
temdeno(1,i)=(sqrt((npoY(1,p)-cpoY(i,1))^2+(npoX(1,q)-cpoX(i,1))^2))^(-power);
end
deno(p,q)=sum(temdeno(:));
end
end
%% IDW求解
temPH=zeros(1,length(cPH));
pPH4=zeros(length(npoY),length(npoX));
for p=1:length(npoY)
for q=1:length(npoX)
for i=1:length(cPH)
temPH(1,i)=cPH(i,1).*((sqrt((npoY(1,p)-cpoY(i,1))^2+(npoX(1,q)-cpoX(i,1))^2))^(-power))./deno(p,q);
end
pPH4(p,q)=sum(temPH(:));
end
end
%% IDW效果圖繪製
scatter3(cpoX,cpoY,cPH);
hold on;
mesh(mnpX,mnpY,pPH4);
title('IDW Results of Organic Matter');
%% IDW驗證1
temdeno4=zeros(1,length(cPH));
deno4=zeros(length(vpoY),length(vpoX));
for p=1:length(vpoY)
for q=1:length(vpoX)
for i=1:length(cPH)
temdeno4(1,i)=(sqrt((vpoY(p,1)-cpoY(i,1))^2+(vpoX(q,1)-cpoX(i,1))^2))^(-power);
end
deno4(p,q)=sum(temdeno4(:));
end
end
%% IDW驗證2
temPH4=zeros(1,length(cPH));
vpPH4=zeros(length(vpoY),1);
for p=1:length(vpoY)
for i=1:length(cPH)
temPH4(1,i)=cPH(i,1).*((sqrt((vpoY(p,1)-cpoY(i,1))^2+(vpoX(q,1)-cpoX(i,1))^2))^(-power))./deno4(p,q);
end
vpPH4(p,1)=sum(temPH4(:));
end
%% 精度計算
MEERan4=mean(vPH-vpPH4);
MEERan41=mean(abs(vpPH4-vPH));
RMSEan4=sqrt(sum(vpPH4-vPH).^2/length(vPH));
COCOan4=corrcoef(vpPH4,(vPH)');
%% 檔案轉存
save 5ph.txt pPH4 -ASCII;
參考文獻
[1] 曹祥會,龍懷玉,周腳根,等.河北省表層土壤有機碳和全氮空間變異特徵性及影響因子分析[J].植物營養與肥料學報,2016,22(04):937-948.
[2] 戴萬宏,黃耀,武麗,俞佳.中國地帶性土壤有機質含量與酸鹼度的關係[J].土壤學報,2009,46(05):851-860.