LeetCode952三部曲之一:解題思路和初級解法(137ms,超39%)
歡迎存取我的GitHub
這裡分類和彙總了欣宸的全部原創(含配套原始碼):https://github.com/zq2599/blog_demos
題目描述
- 難度:困難
- 程式語言:Java
- 給定一個由不同正整數的組成的非空陣列 nums ,考慮下面的圖:
- 有 nums.length 個節點,按從 nums[0] 到 nums[nums.length - 1] 標記;
- 只有當 nums[i] 和 nums[j] 共用一個大於 1 的公因數時,nums[i] 和 nums[j]之間才有一條邊。
- 返回圖中最大連通元件的大小
- 範例 1:

輸入:nums = [4,6,15,35]
輸出:4
- 範例 2:

輸入:nums = [20,50,9,63]
輸出:2
- 範例 3:
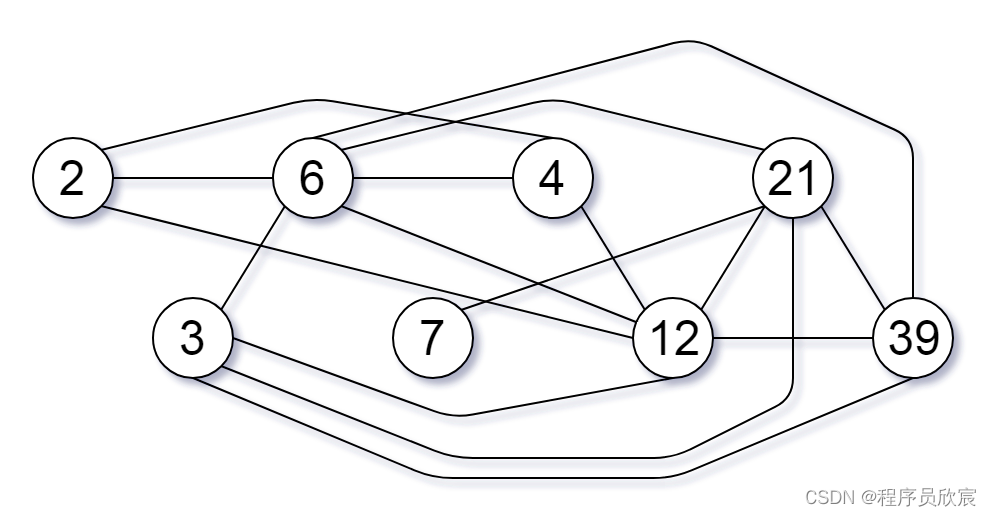
輸入:nums = [2,3,6,7,4,12,21,39]
輸出:8
- 提示:
- 1 <= nums.length <= 2 * 104
- 1 <= nums[i] <= 105
- nums 中所有值都 不同
審題
- 可能是自身天資愚鈍,欣宸第一時間居然沒有搞懂題目中連通元件的大小的含義,以範例一為例,如下圖,明明是三個邊,為啥答案是4?

- 好吧,暈暈乎乎的想了半天終於搞清楚了:
- 不是讓你數有幾條邊!
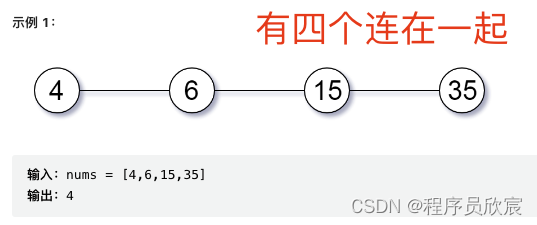
- 是讓你數能夠連在一起的元素,最多有幾個?
- 如下圖,有四個連在一起,答案就是4
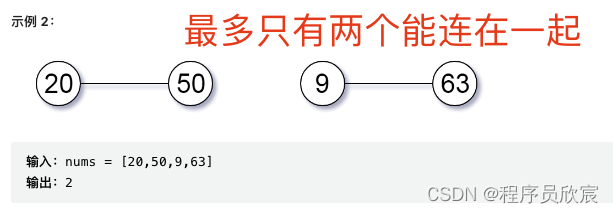
- 如下圖,50和9之間沒有公因數,所以連不起來,導致四個數位中,20和50相連,9和63相連,那麼,能連在一起的兩個組合中,每個組合的數量都是2,答案就是2
- 磕磕絆絆終於讀懂了題,再來看看解題前對知識儲備的要求
需要哪些基本功?
- 請先掌握下面兩個基本功,然後再能愉快的解題和優化,享受AC的喜悅,以及超過人數百分比提升的成就感
- 計算素數(埃氏篩選或者尤拉篩選,我這裡用的是尤拉篩選)
- 並查集,需掌握以下技術點:
- 資料結構是陣列,下標代表數位,值代表父節點是誰
- 查詢(查詢時順便優化路徑)
- 合併
- 上述基本功相信難不倒聰明的您,半小時內就能掌握,接下來,在欣宸圖文並茂的解說中,一起享受解hard題的快樂吧
題目中還有哪些重要資訊?
- 除了基本命題,還有三個至關重要的資訊需要重點關注,他們是解題的關鍵,如下圖,請記住這三個資訊,很快就會用到

- 至此,準備工作已經完成,可以開始分析解題思路了,圖文並茂的分析中,可能會讓您產生一個錯覺:hard題,就這?
解題思路
- 先畫個圖來描述完整流程
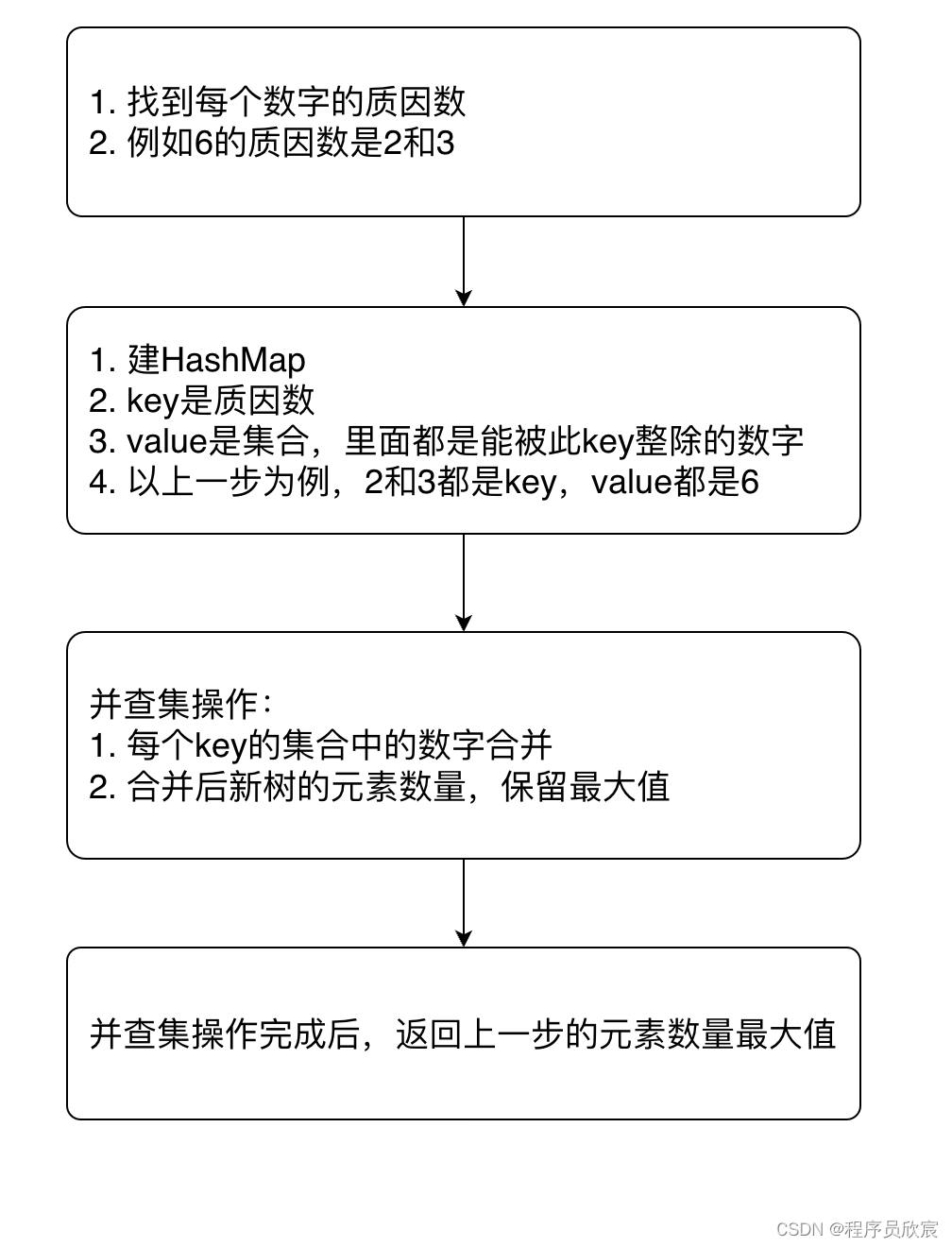
- 上面這個圖,一開始可能您會看得有點暈乎,HashMap到底存了啥?並查集合並又合併了啥?
- 看不明白沒事,真的沒事,此圖其實是解題思路的提前小結,接下來咱們用實際數位來演示解題思路,總之,就是要以最簡單和具體的手段讓您理解思路
範例解題演示解題思路
- 注意,接下來還是分析思路,暫時不涉及程式碼
- 以官方的範例來演示解題過程吧,假設輸入陣列有四個數位:4、6、15、35
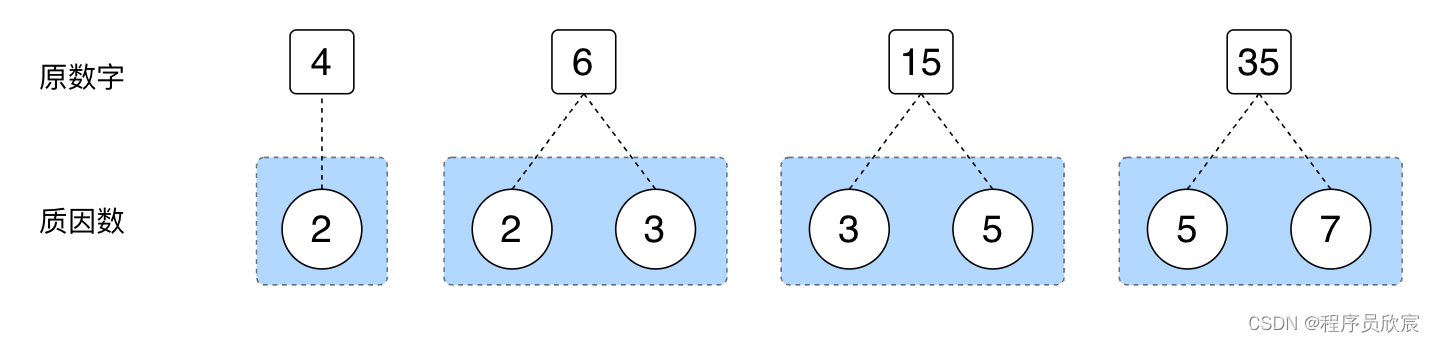
- 首先,計算出每個數位的質因數,如下圖,4的質因數是2,6的質因數是2和3,應該很好理解
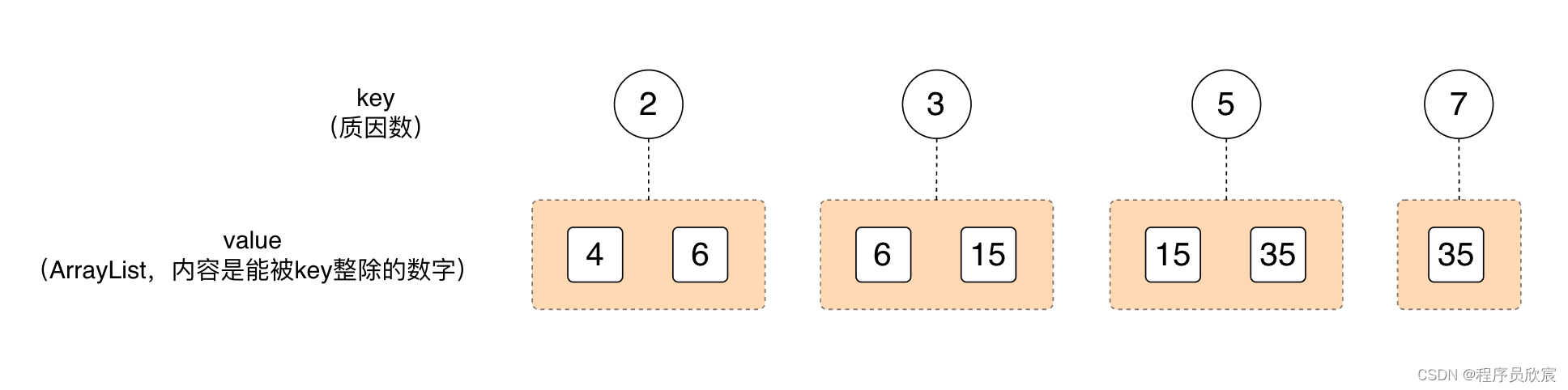
- 接下來,根據上面的計算結果,新建一個HashMap,key是質因數,value是原數位,以2為例,它是4和6的質因數,所以,key就是2,value是個ArrayList,裡面的內容是4和6,也就是說,根據上面的圖得出下面的圖
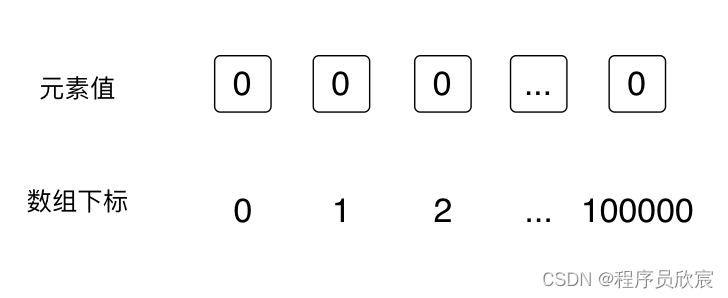
- 現在新建一個並查集,由於數位大小範圍是從1到100000,所以,為了用陣列下標表示數位,組數的大小就是100001,如此一來,array[100000]=123的意思就是:100000這個數位的父節點是123,這就是並查集概念中的陣列定義的標準含義了
- 注意,陣列建立後,每個元素值都是0,如下圖
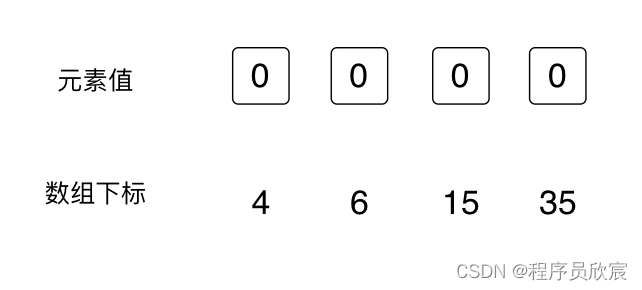
- 在本題中,咱們只關心4、6、15、35這四個數位,所以接下來畫圖的時候,陣列中其他數位就不畫上去了,後面的分析中,陣列畫出來就是下圖的效果,相信您可以理解
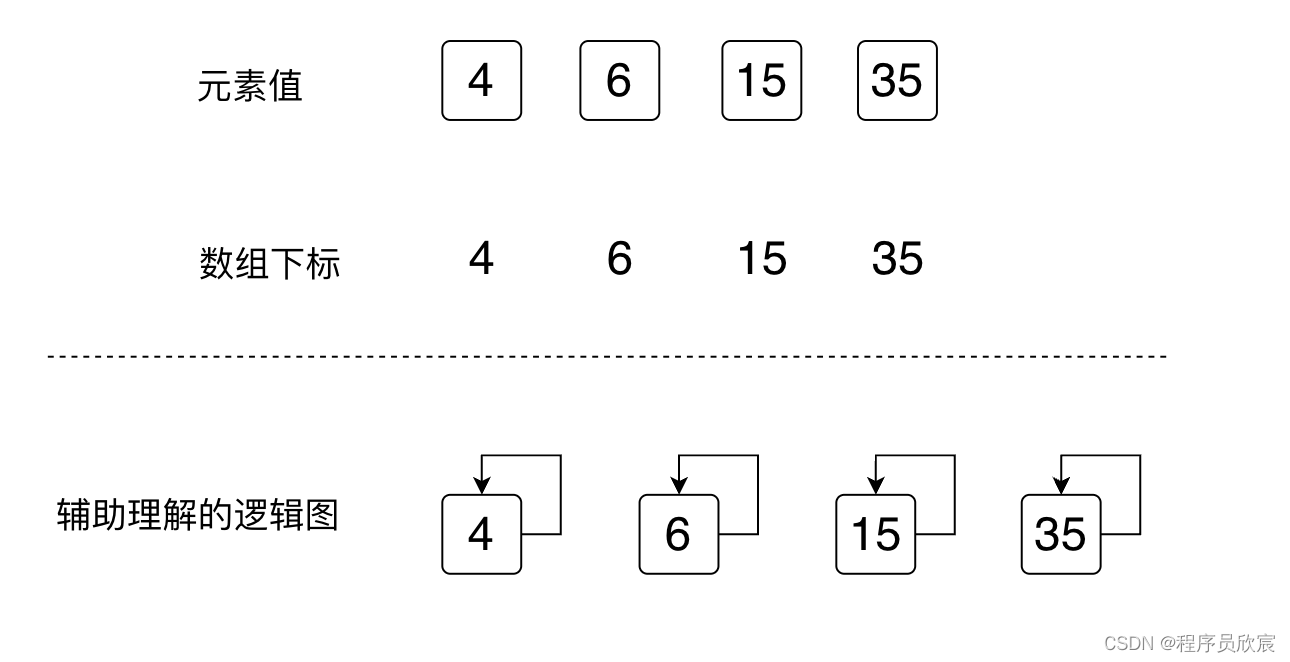
- 按照並查集的定義,最初的時候,每個元素的父節點是它自己,所以給陣列中每個元素賦值,值就等於陣列下標,如下圖所示,注意下圖新增了輔助理解的邏輯圖,這個是用來幫助大家理解每個節點和父節點關係的,可以看到每個節點的箭頭指向自己,表示自己是自己的父節點(或者說每個元素都是根節點)
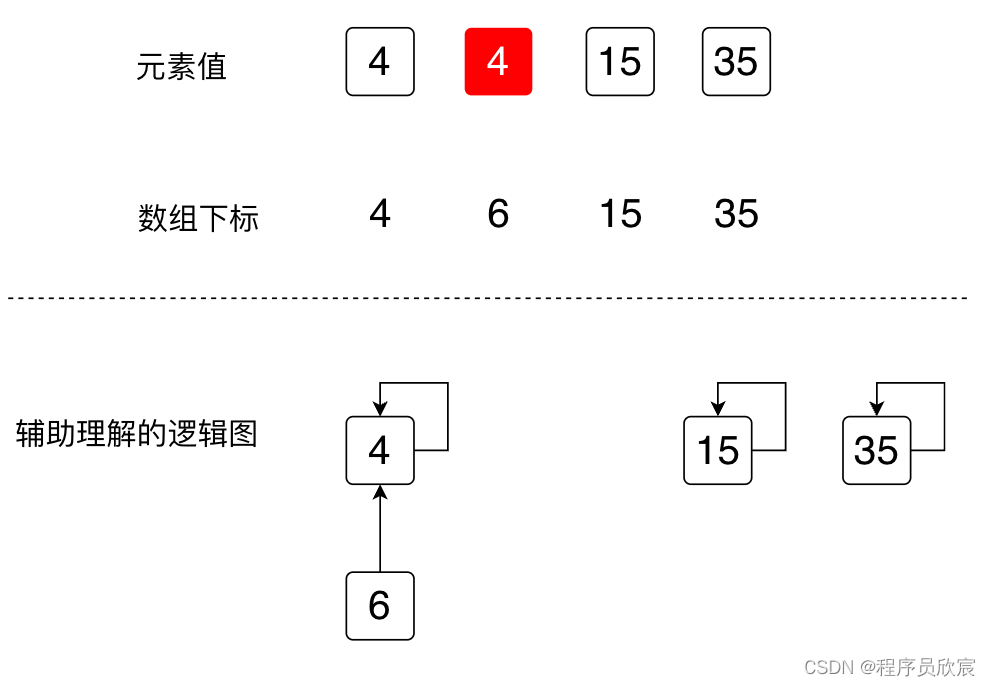
- 接下來,遍歷前面準備好的HashMap,每個key對應的都是一個List,將這個list中的所有元素在並查集中合併,以key等於2為例,value中有兩個數位:4和6,所以,在並查集中將4和6合併
- 第一個key是2,value中的數位是4和6,將4和6合併的效果如下圖,紅色是改過的地方,值等於4,表示數位6的父節點改成了4,為了便於理解,邏輯圖也同步改動了,6指向自己的父節點4
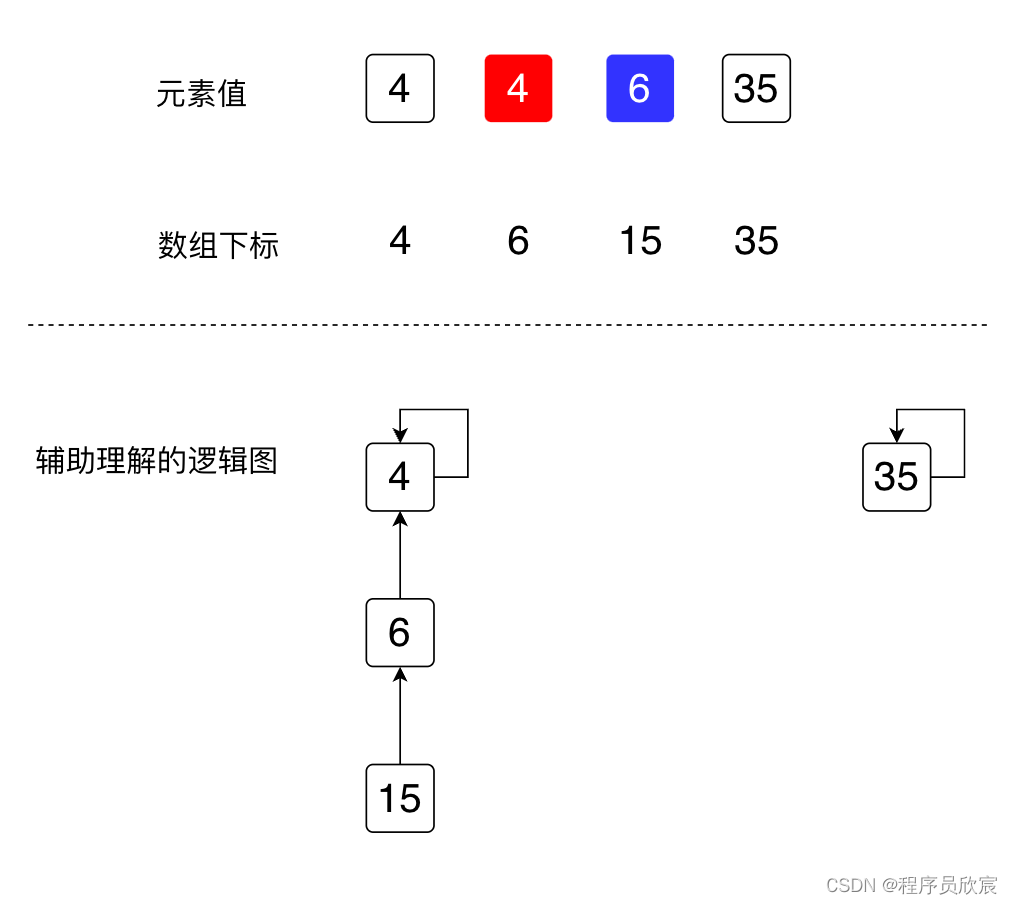
- 第二個key是3,value中的數位是6和15,將6和15合併的效果如下圖,藍色是改過的地方,值等於6,表示數位15的父節點改成了6,為了便於理解,邏輯圖也同步改動了,15指向自己的父節點6(邏輯圖上可見,儘管只改了15的父節點,然而4,6,15已經在同一個樹下了)
- 第三個key是5,value中的數位是15和35,將15和15合併的效果如下圖,綠色是改過的地方,值等於15,表示數位35的父節點改成了15,為了便於理解,邏輯圖也同步改動了,35指向自己的父節點15
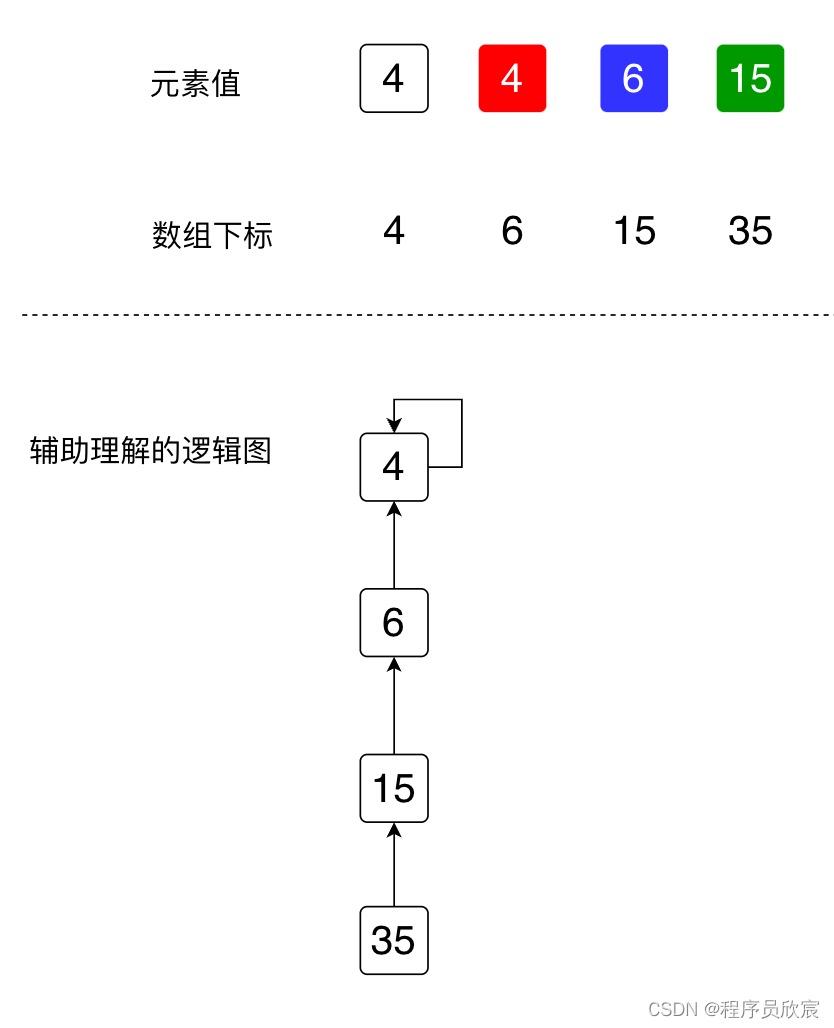
- 至於第四個key,即7,它的value中只有一個數位35,談不上合併,所以不做任何操作
- 至此,並查集合並操作完成,縱觀整個並查樹,雖然有多個樹,唯有以4為根節點的樹,其元素最多,有四個,所以,此題返回值就是4,連通的四個元素是4-6-15-35
- 畫圖畫到手抽筋,相信您對解題思路已經完全掌握,接下來,開始編碼吧
編碼
- 接下來的編碼,先將幾個關鍵點逐個列舉,然後再給出完整程式碼,並且會附上詳細的註解,相信您可以輕鬆讀懂
- 首先看看要定義哪些成員變數,如下,map是最重要的,剛才咱們詳細分析過,程式碼註解也說得很細緻了,然後是fathers、rootSetSize、maxRootSetSize都是並查集相關的資料結構
// 並查集的陣列, fathers[3]=1的意思是:數位3的父節點是1
int[] fathers = new int[100001];
// 並查集中,每個數位與其子節點的元素數量總和,rootSetSize[5]=10的意思是:數位5與其所有子節點加在一起,一共有10個元素
int[] rootSetSize = new int[100001];
// map的key是質因數,value是以此key作為質因數的數位
// 例如題目的陣列是[4,6,15,35],對應的map就有四個key:2,3,5,7
// key等於2時,value是[4,6],因為4和6的質因數都有2
// key等於3時,value是[6,15],因為6和16的質因數都有3
// key等於5時,value是[15,35],因為15和35的質因數都有5
// key等於7時,value是[35],因為35的質因數有7
Map<Integer, List<Integer>> map = new HashMap<>();
// 用來儲存並查集中,最大樹的元素數量
int maxRootSetSize = 1;
- 並查集的查詢根節點的操作也要注意,在查詢過程中,將每個元素的父節點都改成了根節點,這就是常規的壓縮操作
/**
* 帶壓縮的並查集查詢(即尋找指定數位的根節點)
* @param i
*/
private int find(int i) {
// 如果執向的是自己,那就是根節點了
if(fathers[i]==i) {
return i;
}
// 用遞迴的方式尋找,並且將整個路徑上所有長輩節點的父節點都改成根節點,
// 例如1的父節點是2,2的父節點是3,3的父節點是4,4就是根節點,在這次查詢後,1的父節點變成了4,2的父節點也變成了4,3的父節點還是4
fathers[i] = find(fathers[i]);
return fathers[i];
}
- 並查集的合併操作也有個細節要注意,每次合併後,根節點下屬元素會增加,將總數統一出來,再和maxRootSetSize比較一下,這樣持續的操作後,maxRootSetSize記錄的就是最大的樹的元素個數
/**
* 並查集合並,合併後,child會成為parent的子節點
* @param parent
* @param child
*/
private void union(int parent, int child) {
int parentRoot = find(parent);
int childRoot = find(child);
// 如果有共同根節點,就提前返回
if (parentRoot==childRoot) {
return;
}
// child元素根節點是childRoot,現在將childRoot的父節點從它自己改成了parentRoot,
// 這就相當於child所在的整棵樹都拿給parent的根節點做子樹了
fathers[childRoot] = fathers[parentRoot];
// 合併後,這個樹變大了,新增元素的數量等於被合併的字數元素數量
rootSetSize[parentRoot] += rootSetSize[childRoot];
// 更像最大數量
maxRootSetSize = Math.max(maxRootSetSize, rootSetSize[parentRoot]);
}
- 在來看一下得到數位的質因數的操作,如下所示:
// 對陣列中的每個數,算出所有質因數,構建map
for (int i=0;i<nums.length;i++) {
int cur = nums[i];
for (int j=2;j*j<=cur;j++) {
// 從2開始逐個增加,能整除的一定是質數
if(cur%j==0) {
map.computeIfAbsent(j, key -> new ArrayList<>()).add(nums[i]);
}
// 從cur中將j的因數全部去掉
while (cur%j==0) {
cur /= j;
}
}
// 能走到這裡,cur一定是個質數,
// 因為nums[i]被除過多次後結果是cur,所以nums[i]能被cur整除,所以cur是nums[i]的質因數,應該放入map中
if (cur!=1) {
map.computeIfAbsent(cur, key -> new ArrayList<>()).add(nums[i]);
}
}
- 關鍵程式碼已經看完了,來看看完整版程式碼
class Solution {
// 並查集的陣列, fathers[3]=1的意思是:數位3的父節點是1
int[] fathers = new int[100001];
// 並查集中,每個數位與其子節點的元素數量總和,rootSetSize[5]=10的意思是:數位5與其所有子節點加在一起,一共有10個元素
int[] rootSetSize = new int[100001];
// map的key是質因數,value是以此key作為質因數的數位
// 例如題目的陣列是[4,6,15,35],對應的map就有四個key:2,3,5,7
// key等於2時,value是[4,6],因為4和6的質因數都有2
// key等於3時,value是[6,15],因為6和16的質因數都有3
// key等於5時,value是[15,35],因為15和35的質因數都有5
// key等於7時,value是[35],因為35的質因數有7
Map<Integer, List<Integer>> map = new HashMap<>();
// 用來儲存並查集中,最大樹的元素數量
int maxRootSetSize = 1;
/**
* 帶壓縮的並查集查詢(即尋找指定數位的根節點)
* @param i
*/
private int find(int i) {
// 如果執向的是自己,那就是根節點了
if(fathers[i]==i) {
return i;
}
// 用遞迴的方式尋找,並且將整個路徑上所有長輩節點的父節點都改成根節點,
// 例如1的父節點是2,2的父節點是3,3的父節點是4,4就是根節點,在這次查詢後,1的父節點變成了4,2的父節點也變成了4,3的父節點還是4
fathers[i] = find(fathers[i]);
return fathers[i];
}
/**
* 並查集合並,合併後,child會成為parent的子節點
* @param parent
* @param child
*/
private void union(int parent, int child) {
int parentRoot = find(parent);
int childRoot = find(child);
// 如果有共同根節點,就提前返回
if (parentRoot==childRoot) {
return;
}
// child元素根節點是childRoot,現在將childRoot的父節點從它自己改成了parentRoot,
// 這就相當於child所在的整棵樹都拿給parent的根節點做子樹了
fathers[childRoot] = fathers[parentRoot];
// 合併後,這個樹變大了,新增元素的數量等於被合併的字數元素數量
rootSetSize[parentRoot] += rootSetSize[childRoot];
// 更像最大數量
maxRootSetSize = Math.max(maxRootSetSize, rootSetSize[parentRoot]);
}
public int largestComponentSize(int[] nums) {
// 對陣列中的每個數,算出所有質因數,構建map
for (int i=0;i<nums.length;i++) {
int cur = nums[i];
for (int j=2;j*j<=cur;j++) {
// 從2開始逐個增加,能整除的一定是質數
if(cur%j==0) {
map.computeIfAbsent(j, key -> new ArrayList<>()).add(nums[i]);
}
// 從cur中將j的因數全部去掉
while (cur%j==0) {
cur /= j;
}
}
// 能走到這裡,cur一定是個質數,
// 因為nums[i]被除過多次後結果是cur,所以nums[i]能被cur整除,所以cur是nums[i]的質因數,應該放入map中
if (cur!=1) {
map.computeIfAbsent(cur, key -> new ArrayList<>()).add(nums[i]);
}
}
// 至此,map已經準備好了,接下來是並查集的事情,先要初始化陣列
for(int i=0;i< fathers.length;i++) {
// 這就表示:數位i的父節點是自己
fathers[i] = i;
// 這就表示:數位i加上其下所有子節點的數量等於1(因為每個節點父節點都是自己,所以每個節點都沒有子節點)
rootSetSize[i] = 1;
}
// 遍歷map
for (int key : map.keySet()) {
// 每個key都是一個質因數
// 每個value都是這個質因數對應的數位
List<Integer> list = map.get(key);
// 超過1個元素才有必要合併
if (null!=list && list.size()>1) {
// 取第0個元素作為父節點
int parent = list.get(0);
// 將其他節點全部作為地0個元素的子節點
for(int i=1;i<list.size();i++) {
union(parent, list.get(i));
}
}
}
return maxRootSetSize;
}
}
- 在LeetCode上提交,結果如下圖,137ms,超過39.55%的使用者

- 至此,初步嘗試已經通過,儘管耗時偏高,39%的比例也過於勉強,但證明本題的解題思路是走得通的
- 本文接下來的篇幅,是對自己在解題過程中犯錯的覆盤,放在這裡供您參考,如果您也有類似困惑,希望接下來的內容可以幫助到您
何為連通?
- 通過因數2可將 4, 6, 12連通,這句話啥意思?在看LeetCode高手們的解題過程時,常常看到他們提到連通,最初我是很難理解這個概念
- 這句話的意思是,因為4,6,12有共同的因數2,所以,4和6可以連線,4和12也可以連線,6和12也可以連線,簡單的說就是有共同因素的數位,它們是可以隨意連線的!
最大的誤解
-
個人在做這道題的時候,最大的誤解就是對並查集合並的理解錯誤,導致做錯,這裡列出來,以避免您犯相同錯誤
-
以4,6,15,35這四個數位為例,以2為質因數的有4和6,以3為質因數的有6和15,以5為質因數的有15和35,以7為質因數的有35,邏輯關係如下圖

-
所以,我們在說並查集合並操作,到底在合併什麼?(這是核心,理解正確,這道題就解開了)
-
之前的誤解如下圖,以為是將紅色箭頭指向的四個集合合併,這樣就達到了連通效果,實際上這樣的理解是大錯特錯

-
接下來是自我救贖的糾正之路
-
首先,圖就是錯誤的,既然是並查集,就應該按照並查集的資料結構來畫圖:一個int陣列,陣列下標就代表具體數位,值代表該數位的父節點是誰,例如 a[2]=5,其含義就是數位2的父節點是5,這是基本定義
-
並查集初始化的時候,每個元素的父節點都是它自己,如下圖,注意,這個陣列的長度其實是36(既從0到35),但是其他元素都用不上,所以我們無需關注它們,也就沒有畫進圖中
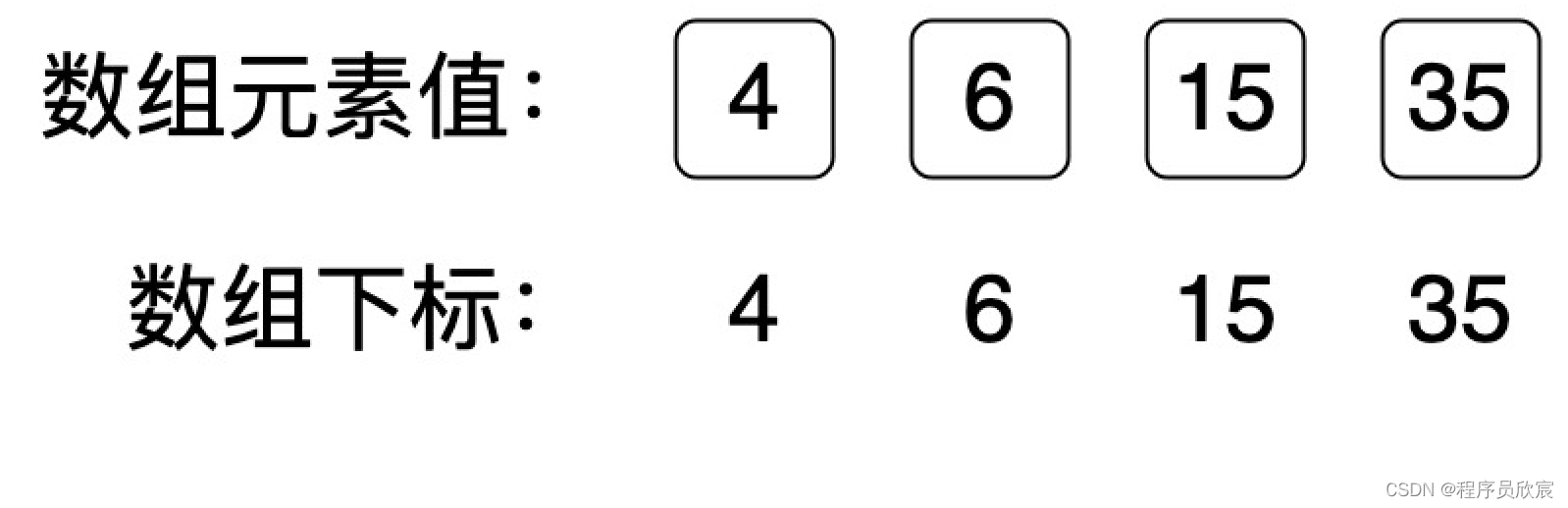
-
接下來就是本題最核心的操作:合併,究竟該怎麼合併呢?
-
答案是:相同質因數的數位合併,也就是說:以2為質因數的是4和6,所以4和6合併,以3為質因數的是6和15,所以6和15合併,以5為質因數的是15和35,所以15和35合併,7的質因數只有35,那就沒法合併了
-
以上就是合併的操作,沒錯,就是這麼簡單:在並查集中對擁有相同質因數的數位進行合併
-
看到這裡,您應該會疑惑:這樣的合併,和連通有什麼關係?和解題又有什麼關係呢?
-
不急,咱能就用上面的陣列,合併一下試試,稍後就會見證奇蹟,也許能幫您找到豁然開朗的感覺
-
為了形象的理解,接下來我給陣列再配上圖,用來更形象的表達元素之間的父子關係,合併前的陣列和關係圖如下圖,每個圓圈都有個箭頭指向自己,表示每個元素的父節點是自己
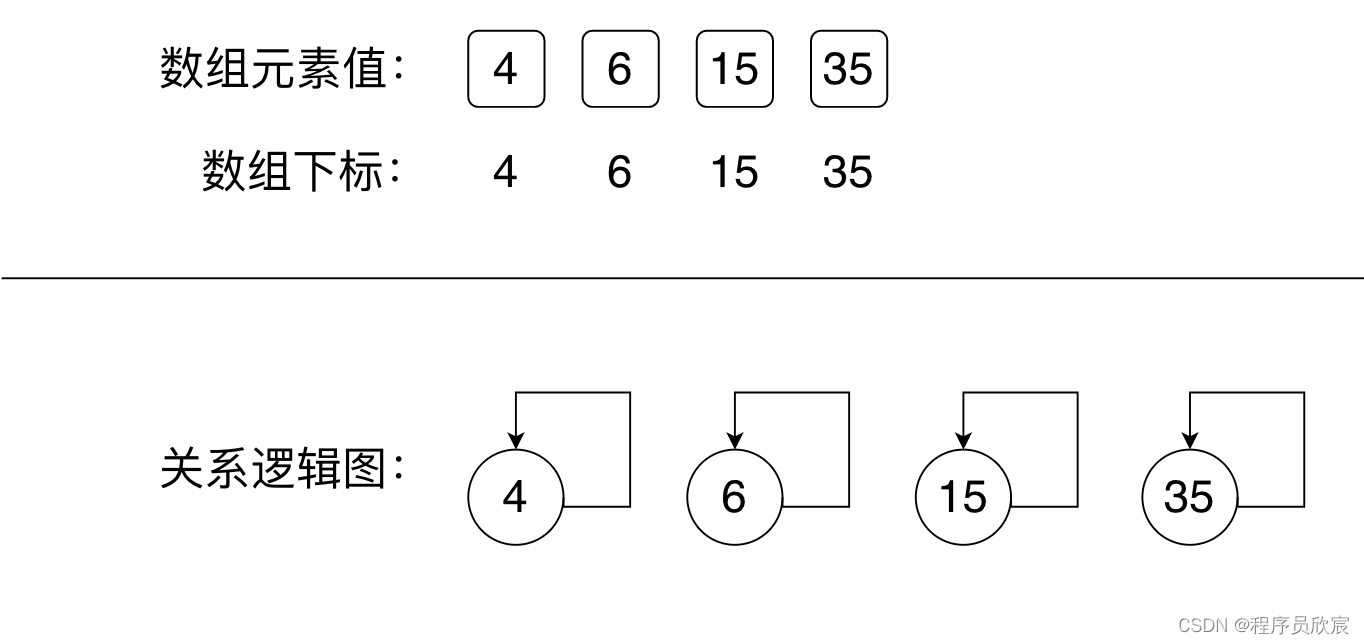
-
接下來,合併4和6,這裡的做法是把4作為6的父節點,所以,如下圖,陣列下標為4的元素值等於6,用邏輯圖來表示,就是6的箭頭指向4

-
接下來該合併6和15了,它們都有質因數3,這一步非常關鍵,因為我就是在這一步恍然大悟的,如下圖,將6的父節點設定為4,再看邏輯關係圖,明明只是在合併6和15,然而,4、6、15已經連通了!
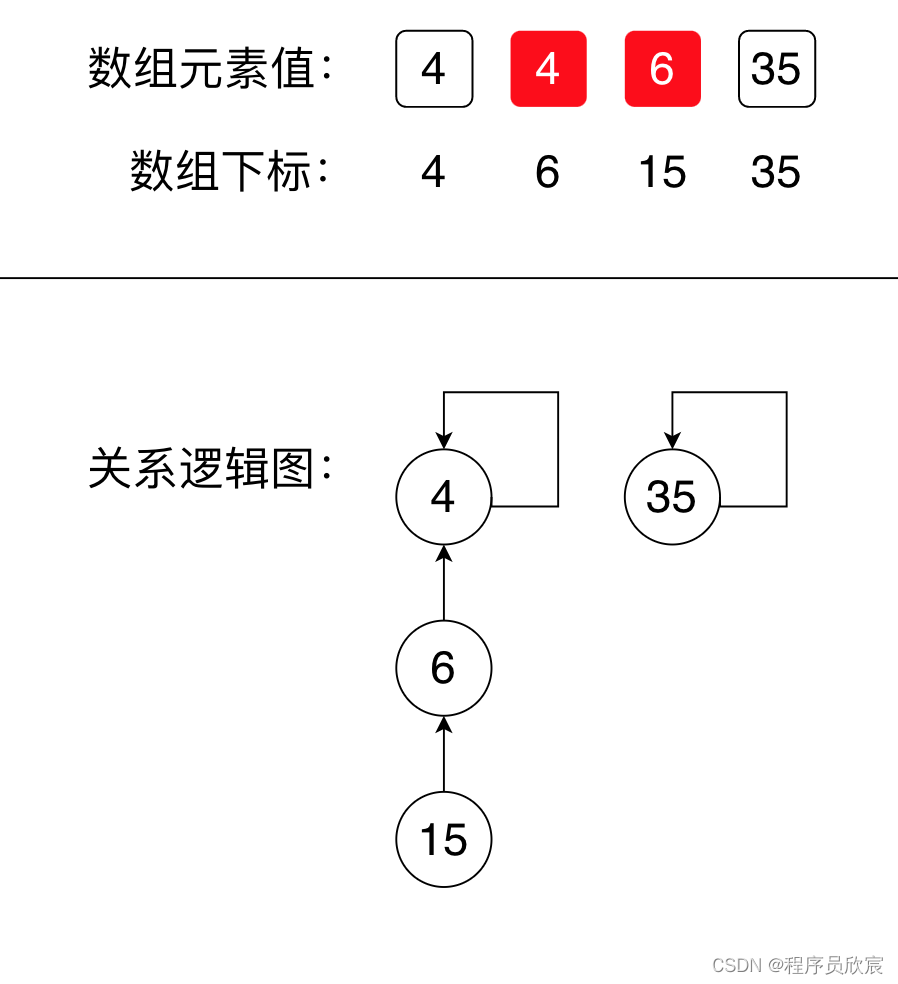
-
恍然大悟:我們無需對各個質因數之間做什麼,只要將每個質因數對應的數位合併即可,有的數位本來就屬於多個質因數,所有跨質因數的連線都是因為這個特點而存在!
-
接下來是連線15和35,相信聰明的您也已經徹底領悟了,此時4個元素已經連通了
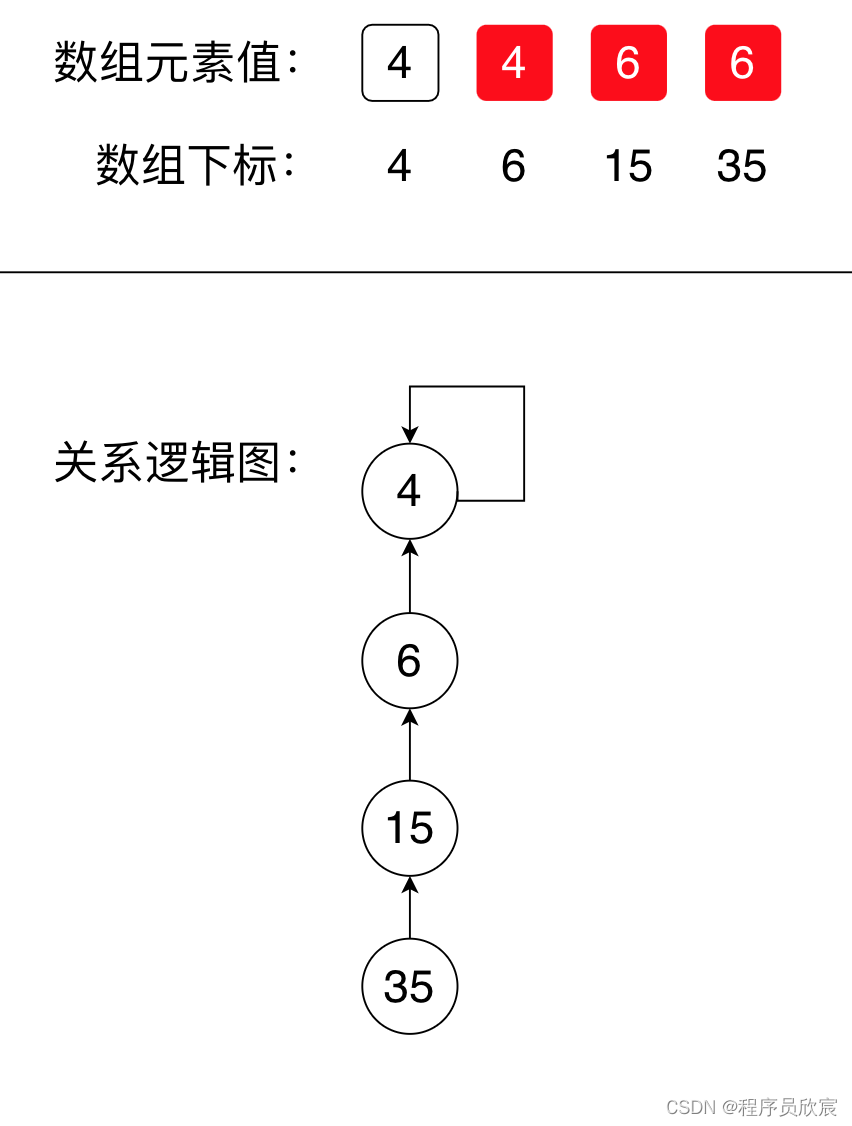
-
最後質因數7對應的數位只有35,一個數位就不需要合併操作了
敬請期待
- 至此,952的解題思路以及最初級的解法實戰已經完成,這麼多圖和範例,相信聰明的您對解答此題已經胸有成竹,然而耗時過長,超39%實在是過於落後了,不能忍,所以,接下來的章節咱們一起來對此題做第一次優化,看看能不能有所提升