技術文章 » C++演演算法之旅、04 基礎篇 | 第一章

C++演演算法之旅、04 基礎篇 | 第一章

2023-09-01 12:00:30

常用程式碼模板1——基礎演演算法 - AcWing

ios::sync_with_stdio(false)

提高 cin 讀取速度，副作用是不能使用 scanf

資料輸入規模大於一百萬建議用scanf


快速排序

基於分治 nlog(n) (期望值)

  1. 確定分界點

    q[L]、q[ (L+R) / 2 ]、q[R]、隨機點

  2. 調整區間 最難部分

    所有 <=x的元素在x左半邊，所有> = x 的元素在 x 右半邊

    暴力做法： 開兩個陣列 a, b，遍歷 q，如果 <=x的元素放a，> x 的元素放 b。把 a、b 的元素分別放入 q 裡面去，q 相當於 a + x + b 。掃了兩遍 O(n)
    優美方法： 開兩個指標 a, b, 同時往中間走，a 先走，直到元素 >= x，i 停下來。移動 j，直到元素 < x，此時兩個指標對應元素互換，各自移動一位

  3. 遞迴處理左右兩段


785 ⭐

785. 快速排序 - AcWing題庫

讀入大量資料時，scanf更快一些。

另外本題有特殊情況，該情況下每次取區間起點或者終點作為分界點，則會超時。分界點換成隨機值，或者區間中點即可。

#include <algorithm>
#include <cstdio>

using namespace std;

const int N = 1e6 + 10;

int n;
int q[N];

void quick_sort(int q[], int l, int r) {
    if (l >= r) return;
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    while (i < j) {
        do i++;
        while (q[i] < x);
        do j--;
        while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
    // ^ 在[1,2]陣列情況下x不能取右邊界點，否則會陷入死迴圈
    // quick_sort(q, l, i-1), quick_sort(q, i, r);
    // ^ 在[1,2]陣列情況下x不能取左邊界點，否則會陷入死迴圈
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &q[i]);
    quick_sort(q, 0, n - 1);
    for (int i = 0; i < n; i++) printf("%d ", q[i]);

    return 0;
}

786

786. 第k個數 - AcWing題庫

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;
int q[N];

void quick_sort(int q[], int l, int r) {
    if (l >= r) return;
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    while (i < j) {
        do i++;
        while (q[i] < x);
        do j--;
        while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

int main() {
    int n, k;
    cin >> n >> k;
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }
    quick_sort(q, 0, n - 1);
    printf("%d", q[k - 1]);

    return 0;
}

歸併排序

基於分治 nlog(n)

  1. 找分界點，mid = (l+r) / 2（歸併是找下標，快排是找數）
  2. 遞迴排序left，right
  3. 歸併，把兩個有序陣列合二為一，使用雙指標法。O(n)，需要額外輔助陣列

排序演演算法的穩定與否，就是排序過程中陣列中兩個相等的資料，經過排序後，排序演演算法能保證其相對位置不發生變化，是穩定排序演演算法。歸併過程中發現兩個相同元素優先放入第一個指標的元素


787 ⭐

787. 歸併排序 - AcWing題庫

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n;
int q[N], tmp[N];

void merge_sort(int q[], int l, int r) {
    if (l >= r) return;
    int mid = l + r >> 1;
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r) {
        if (q[i] <= q[j])
            tmp[k++] = q[i++];
        else
            tmp[k++] = q[j++];
    }
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    for (int i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }
    merge_sort(q, 0, n - 1);
    for (int i = 0; i < n; i++) {
        printf("%d ", q[i]);
    }
    return 0;
}

788 ⭐⭐

788. 逆序對的數量 - AcWing題庫

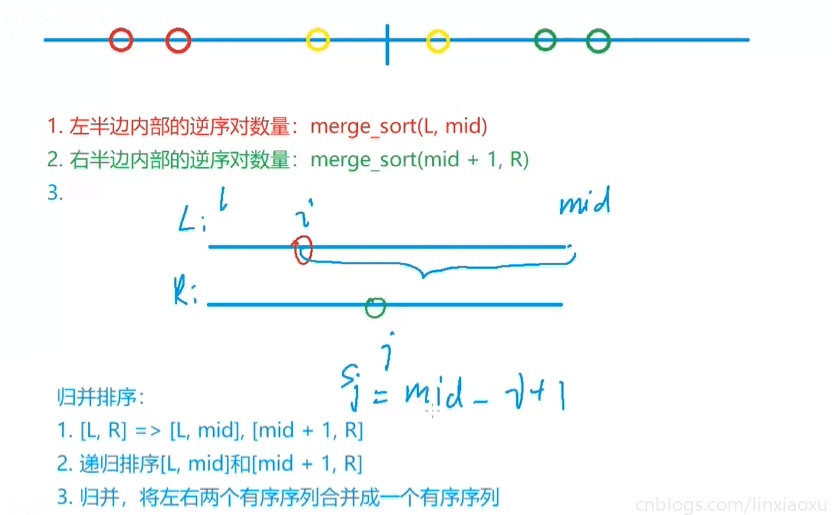
image-20230901105031662

還要考慮逆序對數量，最大數 n * (n - 1) / 2 = 5 * 1e9 大於 INT_MAX，需要用 long long

#include <cstdio>
#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;

int n;
int q[N], tmp[N];

LL merge_sort_count(int q[], int l, int r) {
    if (l >= r) return 0;
    int mid = l + r >> 1;
    int k = 0, i = l, j = mid + 1;
    LL count = merge_sort_count(q, l, mid) + merge_sort_count(q, mid + 1, r);
    while (i <= mid && j <= r) {
        if (q[i] <= q[j])
            tmp[k++] = q[i++];
        else {
            count += mid - i + 1;
            tmp[k++] = q[j++];
        }
    }
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    for (int i = l, k = 0; i <= r; i++, k++) q[i] = tmp[k];
    return count;
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }

    cout << merge_sort_count(q, 0, n - 1);

    return 0;
}

整數二分

image-20230831135750112

整數二分的本質並不是單調性。本質是將區間一分為二，尋找邊界點（左區間邊界還是右區間邊界）。

每次縮短區間一半，答案依舊在縮短的區間內，直到區間長度為1，此時就是邊界點。

二分一定是有解的，此時 l==r，根據二分出來的邊界點判斷題目有沒有解

左區間邊界點

  • 取中點mid = l+r+1 >> 1，判斷該點是否符合左區間性質
    • 如果成立說明mid在左區間，邊界點在 [mid,r]，此時 l = mid
    • 不成立說明mid不在左區間，邊界點在 [l,mid-1]，此時 r = mid-1

右區間邊界點

  • 取中點mid = l+r >> 1，判斷該點是否符合右區間性質
    • 如果成立說明mid在右區間，邊界點在 [l,mid]，此時 r = mid
    • 不成立說明mid不在左區間，邊界點在 [mid+1,r]，此時 l = mid+1

mid分子加1

  • 性質成立條件中：l = mid ，加1；r = mid ，不加1

不加 1，當 l = r - 1 時，由於向下取整，mid = l，當性質條件成立， l = mid = l 死迴圈。加1後，mid = r，不會死迴圈。


789 ⭐

789. 數的範圍 - AcWing題庫

左區間邊界點與右區間邊界點都涉及

#include <cstdio>
#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;

int q[N];

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }
    while (m--) {
        int k;
        cin >> k;
        // ^ 尋找右區間邊界點
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (q[mid] >= k)
                r = mid;
            else
                l = mid + 1;
        }
        if (q[l] != k) {
            cout << "-1 -1" << endl;
            continue;
        } else
            cout << l << " ";
        l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (q[mid] <= k)
                l = mid;
            else
                r = mid - 1;
        }
        cout << r << endl;
    }
    return 0;
}

浮點數二分

浮點數沒有整除向下取整，可以精準一分為二，不需要處理邊界。處理精度問題，加上經驗值2，多處理兩位小數。

// while(r-l >= 1e-8)
for (int i = 0; i < 100; i++) {
    double mid = (l + r) / 2;
    if (mid * mid * mid >= x)
        r = mid;
    else
        l = mid;
}

790 ⭐

790. 數的三次方根 - AcWing題庫

#include <cstdio>
#include <iostream>

using namespace std;

int main() {
    double x;
    cin >> x;
    double l = 0, r = x;
    if (x < -1)  // 負數時調換兩者位置
        l = x, r = 0;
    else if (x > -1 && x < 1)  // 小數時範圍是 [-1,1]
        l = -1, r = 1;

    // while(r-l >= 1e-8)
    for (int i = 0; i < 100; i++) { // 區間長度 / (1 << 100) 
        double mid = (l + r) / 2;
        if (mid * mid * mid >= x)
            r = mid;
        else
            l = mid;
    }
    printf("%lf\n", l);
    return 0;
}

ANTI WEB SPIDER BOT www.cnblogs.com/linxiaoxu

高精度（整數運算）

大整數位數 1e6 ，小整數值 <= 1e9 。（python、java自帶大整數型別）

A + B

791. 高精度加法 - AcWing題庫

#include <cstdio>
#include <iostream>
#include <vector>

using namespace std;

// 加參照符不用拷貝一遍效率更高
vector<int> add(vector<int>& A, vector<int>& B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || i < B.size(); i++) {
        if (i < A.size()) t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(1);
    return C;
}

int main() {
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    auto C = add(A, B);
    for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    return 0;
}

A - B

792. 高精度減法 - AcWing題庫

要保證 A >= B，如果B大，則算 -(B - A) ；如果 A、B 有負數，可以轉換成 |A| - |B| 或 |A| + |B|。

#include <cstdio>
#include <iostream>
#include <vector>

using namespace std;

// 加參照符不用拷貝一遍效率更高
vector<int> sub(vector<int>& A, vector<int>& B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t = A[i] - t;
        // 判斷越界
        if (i < B.size()) t -= B[i];
        // ^ 兩種情況合二為一
        C.push_back((t + 10) % 10);
        t = t < 0 ? 1 : 0;
    }
    // ^ 去掉前導0
    while (C.size() > 1 && C.back() == 0) {
        C.pop_back();
    }
    return C;
}

// 判斷 A>=B
bool cmp(vector<int>& A, vector<int>& B) {
    if (A.size() > B.size())
        return true;
    else if (A.size() < B.size())
        return false;
    else
        for (int i = A.size() - 1; i >= 0; i--) {
            if (A[i] != B[i]) return A[i] > B[i];
        }
    return true;
}

int main() {
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    if (cmp(A, B)) {
        auto C = sub(A, B);
        for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    } else {
        auto C = sub(B, A);
        cout << '-';
        for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    }
    return 0;
}

A * b

793. 高精度乘法 - AcWing題庫

把 b 看成一個整體去和 A 一位一位乘；記得處理b為0時的特殊情況、還有高位進位

#include <cstdio>
#include <iostream>
#include <vector>

using namespace std;

vector<int> mul(vector<int> A, int b) {
    if (b == 0) return vector<int>{0};
    vector<int> C;
    int t = 0; // 進位
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) {
        A.push_back(a[i] - '0');
    }

    auto C = mul(A, b);
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
    return 0;
}

A / b

794. 高精度除法 - AcWing題庫

#include <algorithm>
#include <cstdio>
#include <iostream>
#include <vector>

using namespace std;

// A / b 商 C 餘 r
vector<int> div(vector<int> A, int b, int& r) {
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i--) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) {
        A.push_back(a[i] - '0');
    }
    int r;
    auto C = div(A, b, r);
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
    cout << endl << r << endl;
    return 0;
}

一維字首和

字首和、差分是一對逆運算。字首和下標從 1 開始，\(Si = a_1 + a_2 + ... + a_i\)，\(S_0 = 0\)

\(S[i] = S[i-1] + a_i\) ，預處理 O(n)

重要應用

算 [L,R] 區間內元素和，迴圈遍歷需要 O(n) 複雜度。而使用字首和 \(S_r - S_{l-1}\) 複雜度為 O(1)

下標從1開始

下標從1開始方便處理邊界，求 [1,10] 等於 \(S_{10}-S_{0}\)

若下標從0開始\(S_9 - S_{-1}\)，需要判斷後一項不存在的情況


795

795. 字首和 - AcWing題庫

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int s[N];

int main() {
    int n, m;
    cin >> n >> m;
    int a;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a);
        s[i] = a + s[i - 1];
    }
    while (m--) {
        int l, r;
        cin >> l >> r;
        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

二維字首和

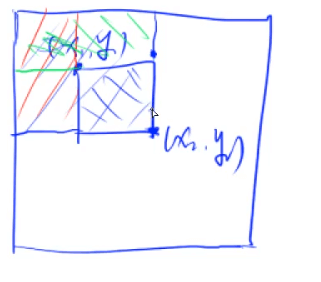
image-20230901020830282

計算各個S

\(S_{x,y} = a_{i,j} + S_{i-1,j} + S_{i,j-1} - S_{i-1,j-1}\)

計運算元矩陣

\(S_{(x_1,y_1),(x_2,y_2)} = S_{x_2,y_2} - S_{x_2,y_1-1} - S_{x_1-1,y_2} + S_{x_1-1,y_1-1}\)


796

796. 子矩陣的和 - AcWing題庫

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e3 + 10;

int S[N][N];

int main() {
    int n, m, q;
    cin >> n >> m >> q;
    int a;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            scanf("%d", &a);
            S[i][j] = a + S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1];
        }
    }
    while (q--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        int res = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1];
        cout << res << endl;
    }
    return 0;
}

一維差分

b為a的差分，a為b的字首和。\(b_1 = a_1\) , \(b_n = a_n - a_{n-1}\)

字首和轉差分

假想字首和全為0，此時差分全為0。然後模擬插入，即字首和 [1,1] 元素加上 \(a_1\)，[2,2] 元素加上 \(a_2\)，[n,n] 元素加上 \(a_n\)

797

797. 差分 - AcWing題庫

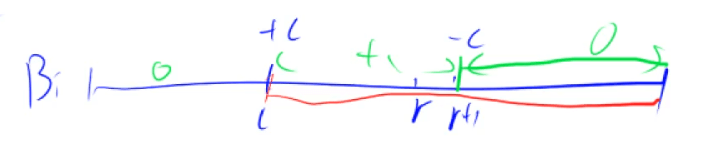
image-20230901023819859

由 b 陣列（差分）得到 a 陣列（字首和）O(n)

給 [L,R] 每個數加上 c，每次操作暴力方法 O(n)，使用差分 O(1)

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int a[N], b[N];

void insert(int l, int r, int c) {
    b[l] += c;
    b[r + 1] -= c;
}

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    // 字首和轉差分
    for (int i = 1; i <= n; i++) {
        insert(i, i, a[i]);
    }
    int l, r, c;
    while (m--) {
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    // 差分轉字首和
    for (int i = 1; i <= n; i++) b[i] += b[i - 1];
    for (int i = 1; i <= n; i++) cout << b[i] << " ";
    return 0;
}

二維差分

構造 \(b_{ij}\) 滿足 \(a_{ij} = \sum_{1}^{n}\sum_{1}^{m}b_{ij}\)

子矩陣全加c

\(b_{x_1,y_1} += c \\ b_{x_{2}+1,y_1} -= c \\ b_{x_1,y_{2}+1} -=c \\b_{x_{2} + 1,y_{2} +1} += c\)

字首和轉差分

假想字首和全為0，此時差分全為0。然後模擬插入，即模擬子矩陣 [1 , 1][1 , 1] 加 c


798

798. 差分矩陣 - AcWing題庫

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e3 + 10;

int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c) {
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main() {
    int n, m, q;
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) insert(i, j, i, j, a[i][j]);

    while (q--) {
        int x1, x2, y1, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            b[i][j] = b[i][j] + b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) cout << b[i][j] << " ";
        cout << endl;
    }

    return 0;
}

雙指標演演算法

用於把樸素演演算法優化到 O(n)

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 具體問題的邏輯
}

第一類雙指標

指向兩個序列，用兩個指標維護一段區間

第二類雙指標

指向一個序列，如快排。維護某種次序，比如歸併排序中合併兩個有序序列的操作


799 ⭐⭐ 第一類

799. 最長連續不重複子序列 - AcWing題庫

資料量 1e5 ，用陣列統計出現次數。當資料量很大時用雜湊表做

從樸素演演算法看 i，j 的單調關係，然後套用雙指標。兩個指標 [i,j] 維護一個最長不重複序列區間。i，j 一定是往右走的（單調性），若 i 往左走則與最長不重複序列區間矛盾。

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int a[N], b[N];

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int count = 0;
    for (int i = 0, j = 0; j < n; j++) {
        b[a[j]]++;
        while (b[a[j]] > 1) {
            b[a[i]]--;
            i++;
        }
        count = max(j - i + 1, count);
    }
    cout << count;
    return 0;
}

800 第二類

800. 陣列元素的目標和 - AcWing題庫

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int a[N], b[N];

int main() {
    int n, m, x;
    cin >> n >> m >> x;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    for (int i = 0; i < m; i++) {
        scanf("%d", &b[i]);
    }
    for (int i = 0, j = m - 1; i < n && a[i] < x; i++) {
        while (j >= 0 && b[j] > x - a[i]) j--;
        if (a[i] + b[j] == x) {
            cout << i << " " << j;
            break;
        }
    }
    return 0;
}

2816 第二類

2816. 判斷子序列 - AcWing題庫

由於堆陣列初始化預設為0，如下輸入會導致 i 最終為 2(i) 而不是 1(n)，在最後的判斷中輸出 No。因此向右移動 i 時需要新增一個 i<n 的條件，避免將陣列外元素納入判斷。

1 2
1
1 0


#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int a[N], b[N];

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    for (int i = 0; i < m; i++) {
        scanf("%d", &b[i]);
    }
    // i 是 a 指標，j 是 b 指標
    int i, j;
    for (i = 0, j = 0; j < m; j++) {
        if (i < n && a[i] == b[j]) i++;  // 注意 i < n
    }
    if (i == n)
        cout << "Yes";
    else
        cout << "No";
    return 0;
}

位運算

原碼、反碼、二補數

  • 原碼 x = 00001010
  • 反碼 x = 11110101
  • 二補數 x = 11110110 （反碼+1）

計算機底層實現沒有減法，只能用加法來做減法


求某一位數位

int i = a >> 2 & 1;

返回最後一位1 lowbit

a & (~a + 1) // 0000001000
// 整數x的負數是取反x後加1
// -a 等同 ~a+1
a & -a

801

801. 二進位制中1的個數 - AcWing題庫

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int a[N];

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    for (int i = 0; i < n; i++) {
        int count = 0;
        while (a[i]) {
            a[i] -= a[i] & -a[i];
            count++;
        }
        cout << count << " ";
    }
    return 0;
}

整數離散化

值域大 0 ~ 1e9，個數少 1e5。有些題目陣列大小與值域一樣大（如計數器），此時空間不夠，需要整數離散化。如 A[1,3,10000] 對映為 B[1,2,3]，A預設有序

  • A 中可能有重複元素，需要去重
  • 如何算出 x 離散化後的值，二分算第一個 >= x 元素在 A 中的位置 + 1
vector<int> alls; // 儲存所有待離散化的值
sort(alls.begin(), alls.end()); // 將所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重複元素

// 二分求出x對應的離散化的值
int find(int x) // 找到第一個大於等於x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 對映到1, 2, ...n
}

802

802. 區間和 - AcWing題庫

當陣列下標小的時候可以用字首和做，該題區間範圍2e9（跨度大），但稀疏（元素少），可以先整數離散化，然後再字首和

陣列開30萬(n+2m)，插入10萬，查詢20萬

#include <algorithm>
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

typedef pair<int, int> PII;

const int N = 3e5 + 10;

// 差分
int s[N];

vector<int> alls;
vector<PII> add, query;

int find(int x) {
    int l = 0, r = alls.size() - 1;
    while (l < r) {
        int mid = l + r >> 1;
        if (alls[mid] >= x)
            r = mid;
        else
            l = mid + 1;
    }
    return l + 1;
}

int main() {
    int n, m;
    cin >> n >> m;
    while (n--) {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});

        alls.push_back(x);
    }
    for (int i = 0; i < m; i++) {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        alls.push_back(l);
        alls.push_back(r);
    }
    // 去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());

    // 插入
    for (auto item : add) {
        int x = find(item.first);
        s[x] += item.second;
    }

    // 差分轉字首和
    for (int i = 1; i <= alls.size(); i++) s[i] = s[i - 1] + s[i];

    // 處理詢問
    for (auto item : query) {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }
    return 0;
}

unique

本質上是第一類雙指標演演算法

#include <algorithm>
#include <cstdio>
#include <iostream>
#include <vector>

using namespace std;

vector<int> a;

// a 升序序列，i 指標存放當前位置，j 遍歷整個陣列
vector<int>::iterator unique(vector<int>& a) {
    int i = 0;
    for (int j = 0; j < a.size(); j++) {
        if (!j || a[j - 1] != a[j]) a[i++] = a[j];
    }
    // a[0~i-1] 所有不同的數
    return a.begin() + i;
}

// vector<int>::iterator unique(vector<int>& a) {
//     int i = 1;
//     for (int j = 0; j < a.size(); j++) {
//         if (a[i - 1] != a[j]) a[i++] = a[j];
//     }
//     // a[0~i-1] 所有不同的數
//     return a.begin() + i;
// }

int main() {
    int n;
    cin >> n;
    for (int i = 0, x; i < n; i++) {
        scanf("%d", &x);
        a.push_back(x);
    }
    sort(a.begin(), a.end());
    auto x = unique(a);
    for (int i = 0; i < x - a.begin(); i++) {
        cout << a[i] << " ";
    }
    return 0;
}

5
1 2 2 3 3
1 2 3

區間合併

  • 按區間左端點排序
  • 第二個區間對比第一個區間[st,ed]有三種情況
    • 在區間內，不更新
    • 與區間交集，ed更新
    • 在區間外，st,ed更新，更新計數器

803

803. 區間合併 - AcWing題庫

#include <algorithm>
#include <cstdio>
#include <iostream>
#include <vector>

using namespace std;

typedef pair<int, int> PLL;

vector<PLL> a;

vector<PLL> merge(vector<PLL> &segs) {
    vector<PLL> res;
    sort(segs.begin(), segs.end());
    int st = -2e9, ed = -2e9;
    for (auto seg : segs) {
        if (ed < seg.first) {
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first;
            ed = seg.second;
        } else {
            ed = max(ed, seg.second);
        }
    }
    if (st != -2e9) res.push_back({st, ed});
    return res;
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        int l, r;
        cin >> l >> r;
        a.push_back({l, r});
    }

    auto res = merge(a);
    cout << res.size() << endl;
    return 0;
}

759 ⭐ ⭐ 格子染色（美團）

759. 格子染色 - AcWing題庫

  1. 讀入所有行操作，列操作，並排序
  2. 合併行區間，合併列區間
  3. 計算所有行的和 + 列的和 res
  4. res 減去每個行與每個列之間重合點數量
#include <algorithm>
#include <cstdio>
#include <iostream>
#include <vector>

using namespace std;

const int N = 1e5 + 10;

struct Node {
    int no, l, r;
    bool operator<(const Node& w) const {
        if (no != w.no)
            return no < w.no;
        else if (l != w.l)
            return l < w.l;
        else
            return r < w.r;
    }
};

// 用 vector<vector<int>> 會很慢
vector<Node> rows;
vector<Node> cols;

vector<Node> merge(vector<Node> segs) {
    vector<Node> res;
    int no = -2e9, st = -2e9, ed = -2e9;
    for (auto seg : segs) {
        if (st != -2e9 && no != seg.no) {
            res.push_back({no, st, ed});
            no = seg.no;
            st = seg.l;
            ed = seg.r;
        } else {
            no = seg.no;
            if (seg.l > ed) {
                if (st != -2e9) res.push_back({no, st, ed});
                st = seg.l;
                ed = seg.r;
            } else {
                ed = max(seg.r, ed);
            }
        }
    }
    if (ed != -2e9) res.push_back({no, st, ed});
    return res;
}

int main() {
    int n;
    cin >> n;
    // 步驟1 輸入
    while (n--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        if (x1 == x2) {
            rows.push_back({x1, min(y1, y2), max(y1, y2)});
        } else {
            cols.push_back({y1, min(x1, x2), max(x1, x2)});
        }
    }
    sort(rows.begin(), rows.end());
    sort(cols.begin(), cols.end());
    // 步驟2 合併區間
    rows = merge(rows);
    cols = merge(cols);
    // 步驟3 計算
    long long res = 0;  // 最大值可以是 (2e9)平方=4e18
    for (int i = 0; i < rows.size(); i++) {
        res += rows[i].r - rows[i].l + 1;
    }
    for (int i = 0; i < cols.size(); i++) {
        res += cols[i].r - cols[i].l + 1;
    }
    // 步驟4 去重
    for (int i = 0; i < rows.size(); i++) {
        for (int j = 0; j < cols.size(); j++) {
            auto row = rows[i];
            auto col = cols[j];
            if (row.l <= col.no && row.r >= col.no && col.l <= row.no &&
                col.r >= row.no)
                res--;
        }
    }
    cout << res;
    return 0;
}