論文解讀(WDGRL)《Wasserstein Distance Guided Representation Learning for Domain Adaptation》
Note:[ wechat:Y466551 | 可加勿騷擾,付費諮詢 ]
論文資訊
論文標題:Wasserstein Distance Guided Representation Learning for Domain Adaptation
論文作者:Jian Shen、Yanru Qu、Weinan Zhang、Yong Yu
論文來源:2018 ACL
論文地址:download
論文程式碼:download
視屏講解:click
1 介紹
動機:受 Wasserstein GAN 的啟發,本文提出了一種學習領域不變特徵表示的新方法,即 WDGRL ;
優勢:瓦瑟斯坦距離對域自適應的理論優勢在於其梯度特性和有希望的泛化界;
貢獻:
- 對公共領域自適應基準的實證研究表明,WDGRL 在領域適應方面優於最先進的表示學習方法;
- WDGRL成功地統一了兩個域分佈,並保持了明顯的標籤區分;
2 相關
$\text{Borel probability measure}$ $\mathbb{P}$ 和 $\mathbb{Q}$ 之間的 $\text{p-th Wasserstein distance}$:
$W_{p}(\mathbb{P}, \mathbb{Q})=\left(\inf _{\mu \in \Gamma(\mathbb{P}, \mathbb{Q})} \int \rho(x, y)^{p} d \mu(x, y)\right)^{1 / p}$
其中:
-
- $\mathbb{P}, \mathbb{Q} \in\left\{\mathbb{P}: \int \rho(x, y)^{p} d \mathbb{P}(x)<\infty, \forall y \in M\right\} $ ;
- $\Gamma(\mathbb{P}, \mathbb{Q})$ 是基於邊緣分佈 $\mathbb{P}$ 和 $\mathbb{Q}$ 的 $M \times M$ 大小的策略;
- $\mu(x, y)$ 是一種隨機策略,在滿足 $x \in \mathbb{P}$ 和 $y \in \mathbb{Q}$ 的情況下,將單位數量的材料從一個隨機位置 $x$ 運輸到另一個位置 $y$ ;
- $\rho(x, y)^{p}$ 代表將單位數量的材料 從 $x \in \mathbb{P}$ 搬到 $y \in \mathbb{Q}$ 需要的成本;
- $W_{p}(\mathbb{P}, \mathbb{Q})$ 代表最小運輸成本;
$W_{1}(\mathbb{P}, \mathbb{Q})= \underset{\|f\|_{L} \leq 1}{\text{sup}} \; \mathbb{E}_{x \sim \mathbb{P}}[f(x)]-\mathbb{E}_{x \sim \mathbb{Q}}[f(x)]$
其中,$\|f\|_{L}= \sup |f(x)-f(y)| / \rho(x, y) $;3 方法
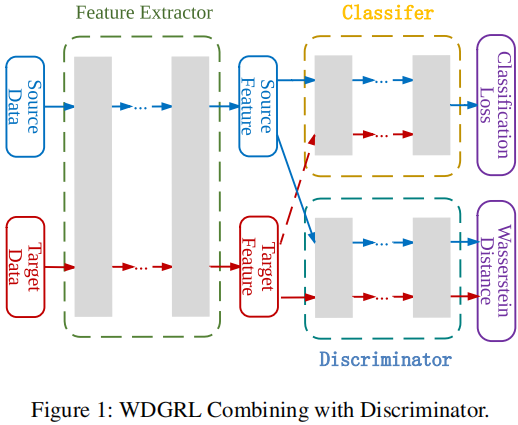
元件:
-
- 特徵提取器 $f_{g}: \mathbb{R}^{m} \rightarrow \mathbb{R}^{d}$;
- 域鑑別器 $f_{w}: \mathbb{R}^{d} \rightarrow \mathbb{R}$;
- 分類器 $f_{c}: \mathbb{R}^{d} \rightarrow \mathbb{R}^{l}$;
3.1 域不變表示學習
為減少源域和目標域之間的差異,使用 域鑑別器,目標是估計源域和目標表示分佈之間的瓦瑟斯坦距離:
$\begin{aligned}W_{1}\left(\mathbb{P}_{h^{*}}, \mathbb{P}_{h^{t}}\right) & = \underset{\left\|f_{w}\right\|_{L} \leq 1}{\text{sup}} \; \mathbb{E}_{\mathbb{P}_{h^{*}}}\left[f_{w}(h)\right]-\mathbb{E}_{\mathfrak{h}^{t}}\left[f_{w}(h)\right] \\& = \underset{\left\|f_{w}\right\|_{L} \leq 1}{\text{sup}} \;\mathbb{E}_{\mathbb{P}_{x^{*}}}\left[f_{w}\left(f_{g}(x)\right)\right]-\mathbb{E}_{\mathbb{P}_{x^{t}}}\left[f_{w}\left(f_{g}(x)\right)\right] \end{aligned}$
如果引數化的域鑑別器函數族 $\left\{f_{w}\right\} $ 都是 $\text{1-Lipschitz}$,那麼可通過最大化關於引數 $\theta_{w}$ 的域鑑別損失 $\mathcal{L}_{w d}$ 來近似經驗瓦瑟斯坦距離:
$\mathcal{L}_{w d}\left(x^{s}, x^{t}\right)=\frac{1}{n^{s}} \sum_{x^{x} \in X^{*}} f_{w}\left(f_{g}\left(x^{s}\right)\right)-\frac{1}{n^{t}} \sum_{x^{t} \in X^{t}} f_{w}\left(f_{g}\left(x^{t}\right)\right)$
關於執行利普希茨約束的問題,Arjovsky 提出,在每次梯度更新後,將域鑑別器的權重剪輯在一個緊湊的空間內 $\text{[−c,c]}$。Gulrajani 指出,權重裁剪將導致梯度消失或爆炸的問題,並提出一種更合理的方法是對域鑑別器引數 $\theta_{w}$ 實施梯度懲罰 $\mathcal{L}_{\text {grad }}$ :
$\mathcal{L}_{\text {grad }}(\hat{h})=\left(\left\|\nabla_{\hat{h}} f_{w}(\hat{h})\right\|_{2}-1\right)^{2}$
其中,懲罰梯度的特徵表示 $\hat{h}$ 不僅定義在源和目標表示上,而且還定義在源和目標表示對之間的直線上的隨機點上。
可通過解決這個問題來估計經驗的瓦瑟斯坦距離:
$\underset{\theta_{w}}{\text{max}}\;\left\{\mathcal{L}_{w d}-\gamma \mathcal{L}_{\text {grad }}\right\}$
最終,表示學習可以通過求解極大極小問題來實現:
$\underset{\theta_{g}}{\text{min}}\; \underset{\theta_{w}}{\text{max}} \; \left\{\mathcal{L}_{w d}-\gamma \mathcal{L}_{\text {grad }}\right\}$
注意,在優化最小操作時,$\gamma$ 應該設定為 $0$,因為梯度懲罰不應該指導表示學習過程;
3.2 鑑別性學習
源域監督學習:
$\mathcal{L}_{c}\left(x^{s}, y^{s}\right)=-\frac{1}{n^{s}} \sum_{i=1}^{n^{s}} \sum_{k=1}^{l} 1\left(y_{i}^{s}=k\right) \cdot \log f_{c}\left(f_{g}\left(x_{i}^{s}\right)\right)_{k}$
3.3 訓練目標
總體訓練目標:
$\underset{\theta_{g}, \theta_{c}}{\text{min}} \; \left\{\mathcal{L}_{c}+\lambda \underset{\theta_{w}}{\text{max}} \; \left[\mathcal{L}_{w d}-\gamma \mathcal{L}_{\text {grad }}\right]\right\}$
3.4 演演算法

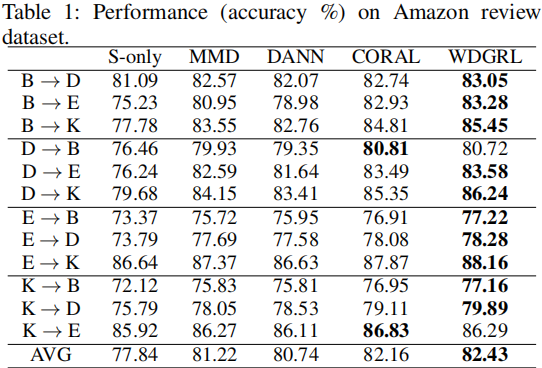
4 實驗
因上求緣,果上努力~~~~ 作者:Wechat~Y466551,轉載請註明原文連結:https://www.cnblogs.com/BlairGrowing/p/17667583.html