numpy中計算相關係數的np.corrcoef

np.corrcoef的作用

計算 Pearson 乘積矩相關係數。它可以用來分析給定資料集中各個變數之間的線性相關程度，返回一個相關係數矩陣,相關係數矩陣中的值介於 -1 到 1 之間，包括 -1 和 1。這些值表明了變數之間的線性相關性及其方向。具體來說，正值接近 1 表示正向線性相關，負值接近 -1 表示負向線性相關，而值接近 0 則表示無線性相關性。

np.corrcoef常用範例

計算二維矩陣的矩陣的相關係數，其中一個維度表示變數variable還有一個維度表示observation表示觀測值,default是row表示variable， column表示observation
其實也比較好理解舉個例子 矩陣[[1,2,3], [4,5,6], [7,8,9]],[1,2,3], [4,5,6],[7,8,9]表示三個隨機變數而這三個隨機變數本身也是一個向量，該向量表示該隨機標量的觀測值即observatin

1. 計算矩陣的皮爾遜係數(不帶其他引數的)

使用np.corrcoef(data), data是一個矩陣,使用預設的row表示variable，column表示observation

import numpy as np 

rng = np.random.default_rng(10)
data = rng.random((3,4))
print("below is data:")
print(data)
res = np.corrcoef(data)
print("------------------------------------------------")
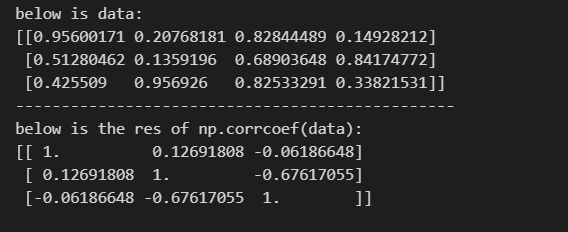
print("below is the res of np.corrcoef(data):")
print(res)

結果如下圖

2. rowvar設定為false來改變預設計算規則來

rowvar設定為false後,row表示observation，column表示variable

import numpy as np 

rng = np.random.default_rng(10)
data = rng.random((3,4))
print("below is data:")
print(data)
res = np.corrcoef(data, rowvar=False)
print("------------------------------------------------")
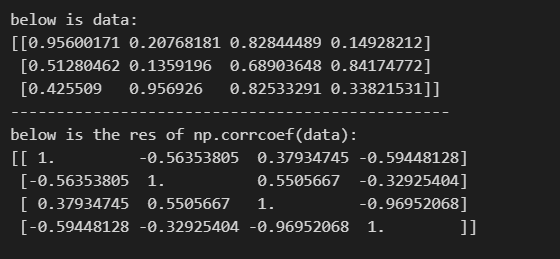
print("below is the res of np.corrcoef(data):")
print(res)

結果如下圖

3. np.corrcoef(data1, data2)

這個其實等效於將data1跟data2在第一個維度上結合後計算皮爾遜相關係數的結果

import numpy as np

a = np.array(([[0.77395605, 0.43887844, 0.85859792],
       [0.69736803, 0.09417735, 0.97562235],
       [0.7611397 , 0.78606431, 0.12811363]]))

b = np.array(([[0.45038594, 0.37079802, 0.92676499],
       [0.64386512, 0.82276161, 0.4434142 ],
       [0.22723872, 0.55458479, 0.06381726]]))

merged_array = np.concatenate((a,b), axis = 0)

res1 = np.corrcoef(a)
res2 = np.corrcoef(a, b)
res3 = np.corrcoef(merged_array)

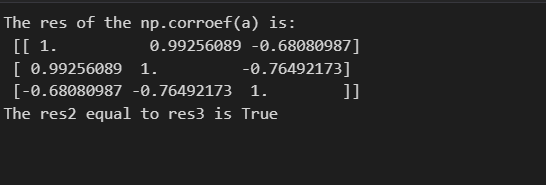
print("The res of the np.corroef(a) is: \n {}".format(res1))
print("The res2 equal to res3 is {}".format(np.array_equal(res2, res3)))

結果如下圖

Reference

1. https://numpy.org/doc/stable/reference/generated/numpy.corrcoef.html