LeetCode 周賽上分之旅 #42 當 LeetCode 考樹上倍增,出題的趨勢在變化嗎
⭐️ 本文已收錄到 AndroidFamily,技術和職場問題,請關注公眾號 [彭旭銳] 和 BaguTree Pro 知識星球提問。
學習資料結構與演演算法的關鍵在於掌握問題背後的演演算法思維框架,你的思考越抽象,它能覆蓋的問題域就越廣,理解難度也更復雜。在這個專欄裡,小彭與你分享每場 LeetCode 周賽的解題報告,一起體會上分之旅。
本文是 LeetCode 上分之旅系列的第 42 篇文章,往期回顧請移步到文章末尾~
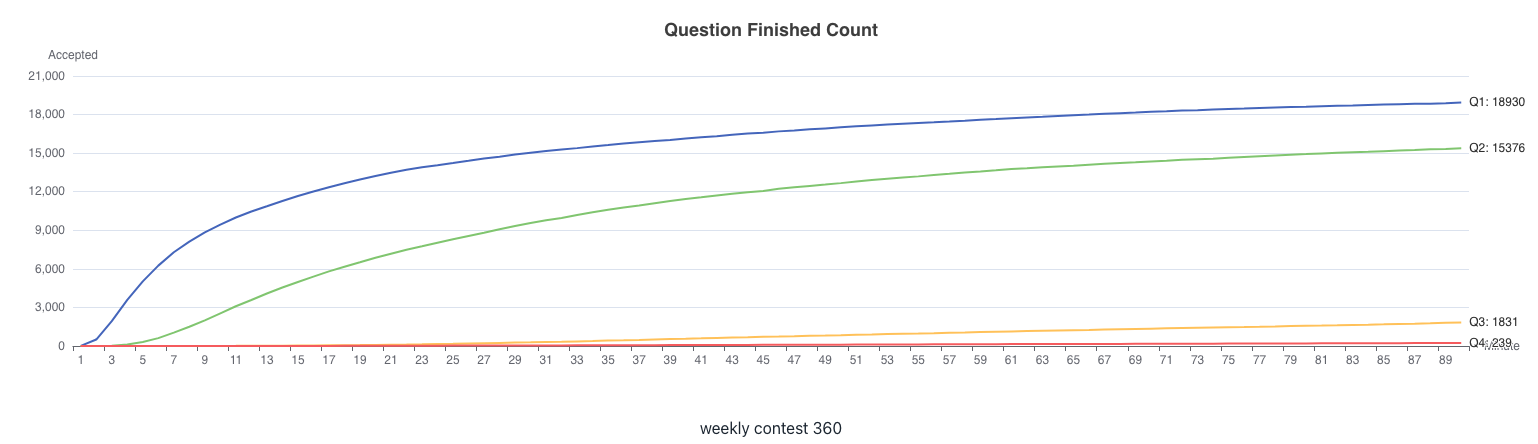
周賽 360
T1. 距離原點最遠的點(Easy)
- 標籤:模擬
T2. 找出美麗陣列的最小和(Medium)
- 標籤:雜湊表、貪心、數學
T3. 使子序列的和等於目標的最少操作次數(Hard)
- 標籤:位運算、雜湊表、排序
T4. 在傳球遊戲中最大化函數值(Hard)
- 標籤:樹、倍增、動態規劃、內向基環樹
T1. 距離原點最遠的點(Easy)
https://leetcode.cn/problems/furthest-point-from-origin/
題解(模擬)
根據題意 「_」 既可以作為 「L」 也可以作為 「R」。容易想到,為了使得終點距離原點更遠,當所有 「_」 僅作為 「L」 或 「R」 對結果的貢獻是最優的,此時問題的結果就取決於 「L」 和 「R」 的差絕對值。
class Solution {
fun furthestDistanceFromOrigin(moves: String): Int {
return moves.count{ it == '_' } + abs(moves.count{ it == 'L' } - moves.count{ it == 'R' })
}
}
一次遍歷:
class Solution {
fun furthestDistanceFromOrigin(moves: String): Int {
var cntL = 0
var cntR = 0
for (e in moves) {
when (e) {
'L' -> {
cntL ++
cntR --
}
'R' -> {
cntL --
cntR ++
}
else -> {
cntL ++
cntR ++
}
}
}
return max(abs(cntL), abs(cntR))
}
}
複雜度分析:
- 時間複雜度:$O(n)$ 線性遍歷;
- 空間複雜度:$O(1)$ 僅使用常數級別空間。
T2. 找出美麗陣列的最小和(Medium)
https://leetcode.cn/problems/find-the-minimum-possible-sum-of-a-beautiful-array/
這道題與上週周賽 359 T2 2829. k-avoiding 陣列的最小總和 相比,除了資料範圍之外是完全相同的,有點離譜。
題解一(雜湊表 + 貪心)
從 $1$ 開始從小到大列舉,如果當前元素 $cur$ 與已選列表不衝突,則加入結果中。為了驗證是否衝突,我們使用雜湊表在 $O(1)$ 時間複雜度判斷。
class Solution {
fun minimumPossibleSum(n: Int, k: Int): Long {
val set = HashSet<Int>()
var sum = 0L
var cur = 1
repeat(n) {
while (!set.isEmpty() && set.contains(k - cur)) cur++
sum += cur
set.add(cur)
cur++
}
return sum
}
}
複雜度分析:
- 時間複雜度:$O(n)$ 線性遍歷;
- 空間複雜度:$O(n)$ 雜湊表空間。
題解二(數學)
這道題還可以繼續挖掘數學規律,我們發現當我們從 $1$ 開始從小到大列舉時,每選擇一個數的同時必然會使得另一個數 $k - x$ 不可選。例如:
- 選擇 $1$,則 $k - 1$ 不可選;
- 選擇 $2$,則 $k - 2$ 不可選;
- …
- 選擇 $k / 2$,則 $k - k / 2$ 不可選。
可以發現,最終選擇的元素被分為兩部分:
- 小於 $k$ 的部分:選擇所有和為 $k$ 的配對中的較小值,即 $1、2、3 … k / 2$;
- 大於等於 $k$ 的部分:與其他任意正整數相加都不會等於 $k$,因此大於等於 $k$ 的數必然可以選擇,即 $k、k + 1、k + 2、…、k + n - m - 1$ 共 n - m 個數。
我們令 $m = min(k / 2, n)$,使用求和公式可以 $O(1)$ 求出兩部分的總和:
- 小於 k 的部分:$m(m + 1)/ 2$
- 大於等於 k 的部分:$(n - m) * (2*k + n - m - 1) / 2$
class Solution {
fun minimumPossibleSum(n: Int, k: Int): Long {
val m = 1L * Math.min(n, k / 2)
return m * (m + 1) / 2 + (n - m) * (2 * k + n - m - 1) / 2
}
}
複雜度分析:
- 時間複雜度:$O(1)$
- 空間複雜度:$O(1)$
T3. 使子序列的和等於目標的最少操作次數(Hard)
https://leetcode.cn/problems/minimum-operations-to-form-subsequence-with-target-sum/
這道題的考點不復雜,難點在模擬問題挺考驗編碼功底的。
問題分析
- 關鍵資訊: $nums$ 陣列中所有元素都是 $2$ 的冪,元素順序對結果沒有影響;
- 問題是否有解: 考慮到所有數最終都能拆分成 $1$,那麼只要 $nums$ 陣列的和大於等於 $target$ 就一定有解;
# 二進位制位
nums: _ _ _ 1 _ _ _ _
target: _ _ _ _ _ 1 _ _
- 子問題: 問題是否有解的判斷不僅適用於原問題,對於僅考慮二進位制位最低位 $[0]$ 到 $[k]$ 的子問題亦是如此。
以範例 1 nums = [1,2,8], target = 7 與範例 2 nums = [1,32,1,2], target = 12 為例,我們將統計 $nums$ 中不同 $2$ 的冪的出現次數:
# 二進位制位
nums: _ _ _ _ 1 _ 1 1
target: _ _ _ _ _ 1 1 1
# 二進位制位
nums: _ _ 1 _ _ _ 1 2 # 1 出現 2 次
target: _ _ _ _ 1 1 _ _
那麼當我們從右向左列舉二進位制位 $k$ 時,如果「$nums$ 中小於等於 $2^k$ 的元素和」$≥$ 「$target$ 中低於等於 $k$ 位的值」,那麼對於僅考慮 $[0, k]$ 位上的子問題是有解的。否則,我們需要找到 $nums$ 中最近大於 $2^k$ 的最近陣列做拆分:
# 只考慮低 2 位,可以構造
nums: _ _ _ _ 1 _ | 1 1
target: _ _ _ _ _ 1 | 1 1
# 只考慮低 3 位,無法構造,需要找到最近的 「1」 做拆分
nums: _ _ _ _ 1 | _ 1 1
target: _ _ _ _ _ | 1 1 1
# 只考慮低 3 位,無法構造,需要找到最近的 「1」 做拆分
nums: _ _ 1 _ _ | _ 1 2
target: _ _ _ _ 1 | 1 _ _
# 只考慮低 6 位,可以構造
nums: _ _ | 1 _ _ _ 1 2
target: _ _ | _ _ 1 1 _ _
組合以上技巧:
寫法一(陣列模擬)
思路參考靈神的題解。
- 首先,我們使用長為 $32$ 的陣列,計算出 $nums$ 陣列中每個 $2$ 的冪的出現次數;
- 隨後,我們從低位到高位列舉二進位制位 $i$,在每輪迭代中將 $nums$ 陣列中的 $2^i$ 元素累加到 $sum$ 中,此舉相當於在求「低 $i$ 位的子問題」可以構造的最大值;
- 最後,我們比較 $sum$ 是否大於等於 $target$(只考慮低 $i$ 位),此舉相當於在判斷「低 $i$ 位的子問題」是否可構造。如果不可構造,我們嘗試尋找最近的 $2^j$ 做拆分;
- 另外,有一個優化點:當我們拆分將 $2^j$ 拆分到 $2^i (j > i)$ 時並不是直接丟棄 $2^j$,而是會留下 $2{j-1}、2… 2^i$ 等一系列數,可以直接跳到第 $j$ 位繼續列舉。
注意一個容易 WA 的地方,在開頭特判的地方,由於元素和可能會溢位 $Int$ 上界,所以我們需要轉換為在 $Long$ 上的求和。
class Solution {
fun minOperations(nums: List<Int>, target: Int): Int {
if (nums.fold(0L) { it, acc -> it + acc } < target) return -1
// if (nums.sum() < target) return -1 // 溢位
// 計數
val cnts = IntArray(32)
for (num in nums) {
var i = 0
var x = num
while (x > 1) {
x = x shr 1
i += 1
}
cnts[i]++
}
var ret = 0
var i = 0
var sum = 0L
while(sum < target) {
// 累加低位的 nums
sum += (cnts[i]) shl i
// println("i=$i, sum=$sum")
// 低 i 位掩碼
val mask = (1 shl (i + 1)) - 1
// 構造子問題
if (sum < target and mask) {
var j = i + 1
while (cnts[j] == 0) { // 基於開頭的特判,此處一定有解
j++
}
// 拆分
ret += j - i
i = j
} else {
i += 1
}
}
return ret
}
}
複雜度分析:
- 時間複雜度:$O(n·U + U$) 其中 $n$ 為 $nums$ 陣列的長度,$U$ 為整型大小 $32$;
- 空間複雜度:$O(U)$ 陣列空間。
寫法二(雜湊表模擬)
在計數的部分,我們可以使用雜湊表模擬,複雜度相同。
class Solution {
fun minOperations(nums: List<Int>, target: Int): Int {
if (nums.fold(0L) { it, acc -> it + acc } < target) return -1
// if (nums.sum() < target) return -1 // 溢位
// 計數
val cnts = HashMap<Int, Int>()
for (num in nums) {
cnts[num] = cnts.getOrDefault(num, 0) + 1
}
var ret = 0
var i = 0
var sum = 0L
while(sum < target) {
// 累加低位的 nums
sum += (cnts[1 shl i] ?: 0) shl i
// println("i=$i, sum=$sum")
// 低 i 位掩碼
val mask = (1 shl (i + 1)) - 1
// 構造子問題
if (sum < target and mask) {
var j = i + 1
while (!cnts.containsKey(1 shl j)) { // 基於開頭的特判,此處一定有解
j++
}
// 拆分
ret += j - i
i = j
} else {
i += 1
}
}
return ret
}
}
複雜度分析:
- 時間複雜度:$O(n + U)$ 其中 $n$ 為 $nums$ 陣列的長度,$U$ 為整型大小 $32$;
- 空間複雜度:$O(U)$ 雜湊表空間。
寫法三(逆向思維)
思路參考雪景式的題解,前兩種寫法是在從小到大列舉「選哪個」,我們也可以列舉「不選哪個」。
- 思考 1: 在原問題有解$(sum > target)$的情況下,如果從 $sum$ 中剔除最大的元素 $x$ 後,依然滿足剩餘的元素和 $sum’ > target$,那麼直接將 $x$ 去掉,這是因為一定存在比 $x$ 操作次數更小的方案能夠構造 $target$(元素越大拆分次數越多)。
- 思考 2: 如果從 $sum$ 中剔除最大的元素 $x$ 後不能構造,說明 $x$ 是一定要選擇或者拆分,此時考慮 $x$ 對 $target$ 的影響:
- 如果 $x > target$,那麼 $x$ 需要先拆分
- 如果 $x ≤ target$,那麼 $x$ 可以被選擇並抵消 $target$
class Solution {
fun minOperations(nums: MutableList<Int>, target: Int): Int {
var sum = nums.fold(0L) { it, acc -> it + acc }
if (sum < target) return -1
// 排序
nums.sortDescending()
// 從大到小列舉
var ret = 0
var left = target
while (sum > left) {
val x = nums.removeFirst()
if (sum - x >= left){
sum -= x
} else if (x <= left) {
sum -= x
left -= x
} else {
ret += 1
nums.add(0, x / 2)
nums.add(0, x / 2)
}
// println("ret=$ret, sum=$sum, left=$left, x=$x, nums=${nums.joinToString()}")
}
return ret
}
}
複雜度分析:
- 時間複雜度:$O(nlgn + n + U)$ 瓶頸在排序,列舉階段每個元素最多存取 $1$ 次,拆分次數最多為 $U$;
- 空間複雜度:$O(lgn)$ 排序遞迴棧空間。
T4. 在傳球遊戲中最大化函數值(Hard)
https://leetcode.cn/problems/maximize-value-of-function-in-a-ball-passing-game/
題解(樹上倍增)
從近期周賽的趨勢看,出題人似乎有意想把 LeetCode 往偏競賽的題目引導。
這道題如果知道樹上倍增演演算法,其實比第三題還簡單一些。
- 問題目標: 找到最佳方案,使得從起點開始傳球 $k$ 次的路徑和最大化;
- 暴力: 對於暴力的做法,我們可以列舉以每名玩家為起點的方案,並模擬傳球過程求出最佳方案。但是這道題的步長 $k$ 的上界非常大 $10^{10}$,如果逐級向上傳球,那麼單次查詢的時間複雜度是 $O(k)$。現在,需要思考如何優化模擬 $k$ 次傳球的效率;
- 倍增思想: 借鑑 1483. 樹節點的第 K 個祖先 的解法,我們可以利用倍增演演算法將線性的操作施加指數級別的貢獻:
- 如果可以預處理出每個玩家的多級後驅玩家,那麼在查詢時可以加速跳轉;
- 由於每個數都可以進行二進位制拆分為多個 $2$ 的冪的和,如果預處理出第 $20、21、22、23、...、2^i$ 個後驅玩家,那麼求解第 $k$ 次傳球時可以轉化為多次 $2^i$ 個後驅玩家跳轉操作,大幅減少操作次數。
class Solution {
fun getMaxFunctionValue(receiver: List<Int>, k: Long): Long {
val n = receiver.size
val m = 64 - k.countLeadingZeroBits()
// 預處理
// dp[i][j] 表示 i 傳球 2^j 次後的節點
val dp = Array(n) { IntArray(m) }
// dp[i][j] 表示 i 傳球 2^j 次的路徑和
val sum = Array(n) { LongArray(m) }
for (i in 0 until n) {
dp[i][0] = receiver[i]
sum[i][0] = receiver[i].toLong()
}
for (j in 1 until m) {
for (i in 0 until n) { // 這道題沒有根節點,不需要考慮 child == -1 的情況
val child = dp[i][j - 1]
// 從 i 條 2^{j-1} 次,再跳 2^{j-1}
dp[i][j] = dp[child][j - 1]
sum[i][j] = sum[i][j - 1] + sum[child][j - 1]
}
}
// 列舉方案
var ret = 0L
for (node in 0 until n) {
var i = node
var x = k
var s = node.toLong() // 起點的貢獻
while (x != 0L) {
val j = x.countTrailingZeroBits()
s += sum[i][j]
i = dp[i][j]
x = x and (x - 1)
}
ret = max(ret, s)
}
return ret
}
}
複雜度分析:
- 時間複雜度:預處理時間為 $O(nlgk)$,列舉時間為 $O(nlgk)$,其中 $n$ 為 $receivers$ 陣列的長度;
- 空間複雜度:預處理空間 $O(nlgk)$。
另外,這道題還有基於「內向基環樹」的 $O(n)$ 解法。
推薦閱讀
LeetCode 上分之旅系列往期回顧:
⭐️ 永遠相信美好的事情即將發生,歡迎加入小彭的 Android 交流社群~
