技術文章 » 強化學習 Proximal Policy Optimization (PPO)

強化學習 Proximal Policy Optimization (PPO)

2023-08-25 18:01:09

參考: 李宏毅老師課件

PPO: Default reinforcement learning algorithm at OpenAI

PPO = Policy Gradient 從 On-policy 到 Off-policy, 再加一些constraint

Policy Gradient

Basic Conception

  • Actor: 動作執行者(智慧體)

  • Env: 環境

  • Reward Function: 獎勵函數

  • Policy \(\pi\) : a network with parameter \(\theta\).

    Input: 當前的 Env.

    Output: actor 要採取的下一個 action 的分佈.

  • Trajectory \(\tau\): 一系列的 Env 和 Action, \(\set{s_1,a_1,s_2,a_2, \dots}\)

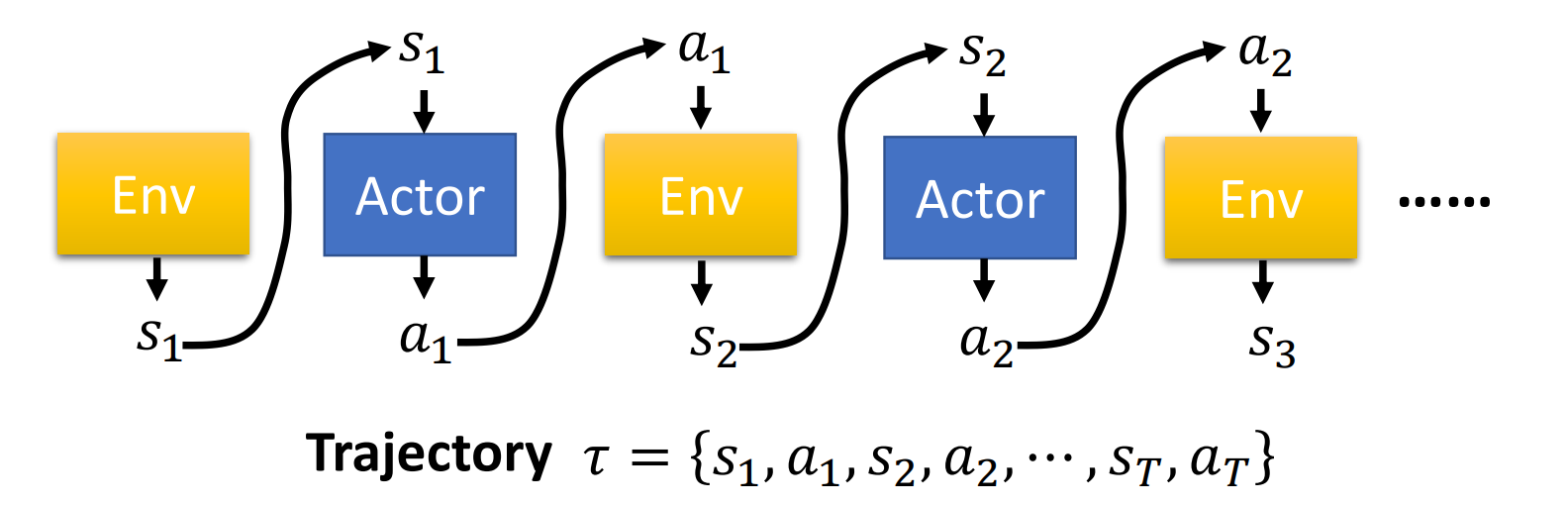
    在引數為 \(\theta\) 情況下, 發生\(\tau\)的概率: \(p_{\theta}(\tau)=p(s_1)p_{\theta}(a_1|s_1)p(s_2|s_1,a_1)p_{\theta}(a_2|s_2)\cdots\)

Optimization

Object


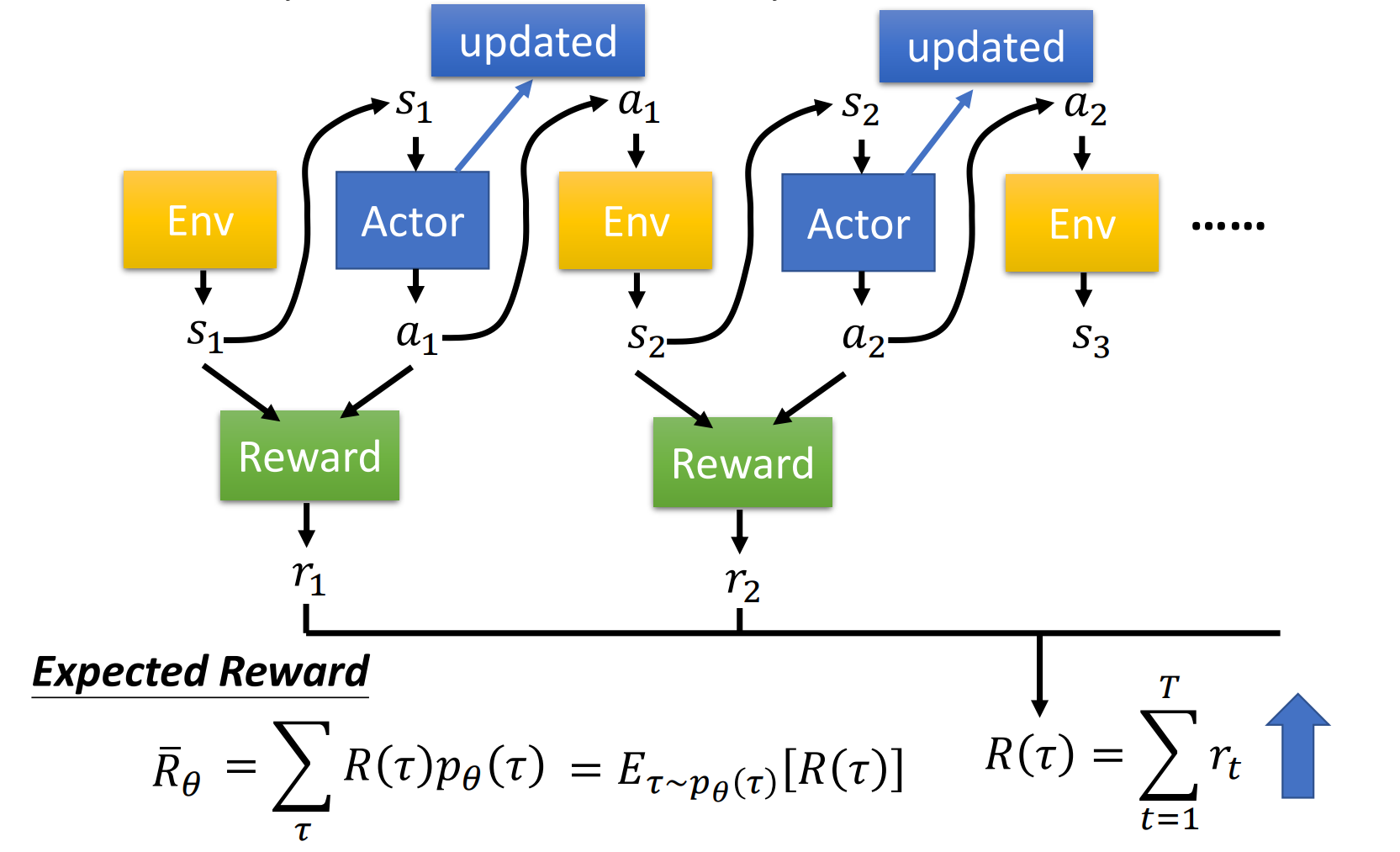
給定 \(\tau\), 可以計算 \(\tau\) 的 reward, \({R(\tau)}\).

對於引數為 \(\theta\) 的 Policy下, Trajectory \(\tau\) 是取樣得到的, 因此實際上需要計算的是 reward 的期望值\(\overline{R_\theta}\). 我們希望 \(\overline{R_\theta}\) 越大越好.

Policy Gradient

Reward 的期望:

\[\begin{equation} \begin{aligned} \overline{R_\theta}=\sum_\tau R(\tau)p_\theta(\tau) \end{aligned} \end{equation} \]

求 \(\theta\) 的梯度:

\[\begin{equation} \begin{aligned} \nabla \overline R_\theta &= \sum_\tau R(\tau)\nabla p_\theta(\tau) \\ &=\sum_\tau R(\tau) p_\theta(\tau) \frac{\nabla p_\theta(\tau)}{p_\theta(\tau)}\quad &&\text{分子分母同乘} p_\theta(\tau)\\ &=\sum_\tau R(\tau) p_\theta(\tau) {\nabla \log p_\theta(\tau)}\\ &=E_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla \log p_\theta(\tau)]\\ &\approx \frac 1 N \sum_{n=1}^{N} R(\tau^n)\nabla \log p_\theta(\tau^n)\\ &= \frac 1 N \sum_{n=1}^{N} \sum_{t=1}^{T_n} R(\tau^n)\nabla \log p_\theta(a^n_t|s^n_t) \end{aligned} \end{equation} \]

由 \(\nabla \log p_\theta(\tau)=\frac{\nabla p_\theta(\tau)}{p_\theta(\tau)}\), 可得到第三行公式.
此處可延伸出一個公式:

\[\begin{equation} \nabla f(x) = f(x) \nabla \log f(x) \end{equation} \]

由\(\sum_\tau p_\theta(\tau)f(\tau)=E_{\tau\sim p_\theta(\tau)}[f(\tau)]\), 可得第四行

通過取樣的方式估計期望值, 取樣 \(N\) 個 Trajectory, 既第五行公式

最後將 \(p_\theta(\tau)\) 展開代入, 得第六行公式

Implementation

最大化 Reward 的期望 \(\overline{R_\theta}\), 由公式(2)中梯度的計算, 可以反推出目標函數在實現時定義如下:

\[\begin{equation} \begin{aligned} J(\theta) = \frac 1 N \sum_{n=1}^{N} \sum_{t=1}^{T_n} R(\tau^n) \log p_\theta(a^n_t|s^n_t) \end{aligned} \end{equation} \]

最大化 \(object\) 等價於最小化 \(loss\):

\[\begin{equation} \begin{aligned} loss = -\frac 1 N \sum_{n=1}^{N} \sum_{t=1}^{T_n} R(\tau^n) \log p_\theta(a^n_t|s^n_t) \end{aligned} \end{equation} \]

其中, \(a^n_t, s^n_t\) 是在引數為 \(\theta\) 的 policy 下取樣得到的.

與交叉熵損失對比: 其實就是將取樣得到的 \(a^n_t\) 視作grand truth計算交叉熵, 區別在於針對不同的 Trajectory \(\tau^n\), 要多乘了一個 \(R(\tau^n)\)

Tips

Add a baseline


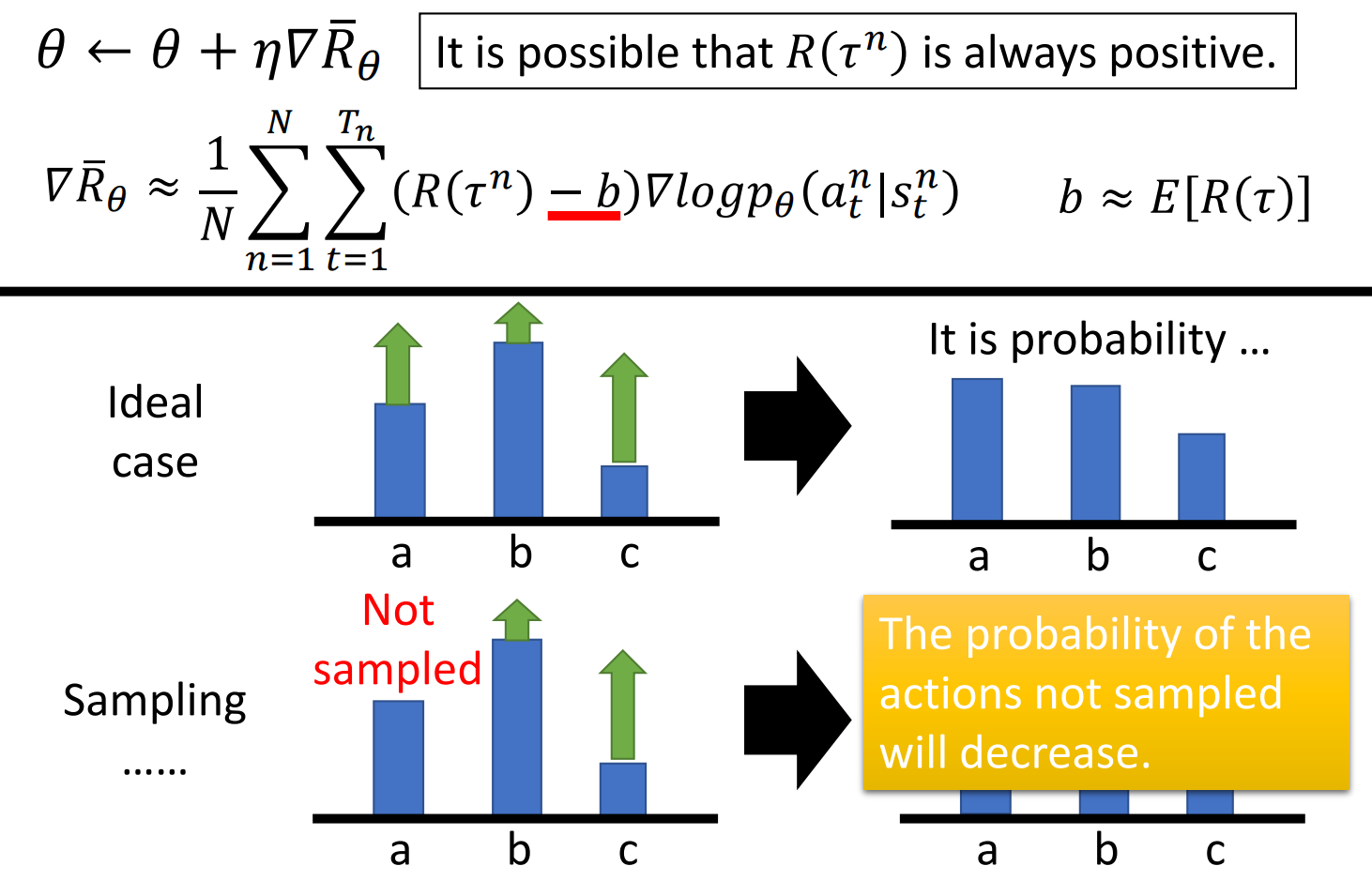
\(R(\tau^n)\) 可能總為正數, 這樣在 training時, 相當於告訴 model, 不論時什麼action 都要將它的概率提升.

理想情況下, 這樣是沒有問題的, 因為 Reward 即使總是正的, 也有大有小.

當時實際上, action 是取樣得到的, 這會導致如果有的 action 沒有被取樣到, 它的概率相對於被取樣到的 action 就會下降, 而這時, 並不能表示當前環境下采取這個 action 不好.

改進: 減去一個 baseline, \(b\).

Assign Suitable Credit


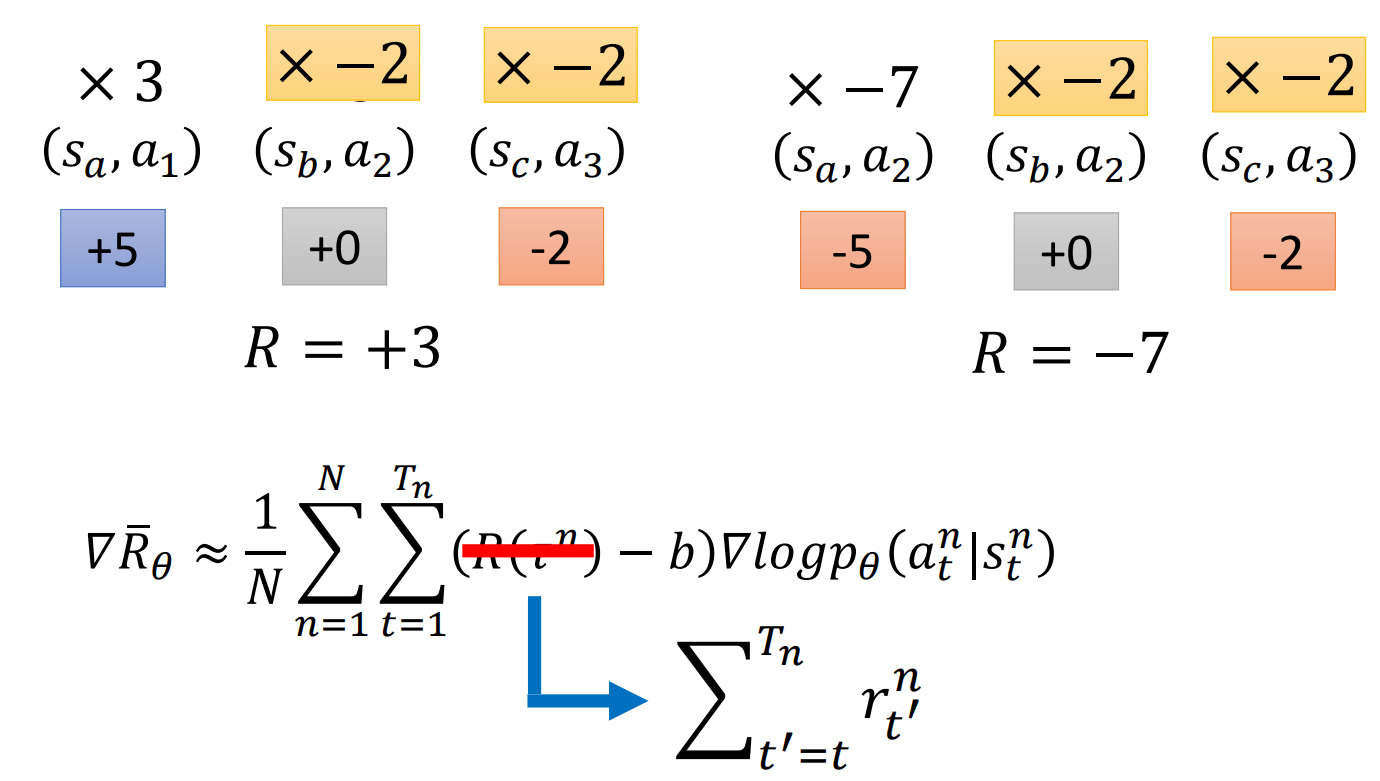
再來看一下目標函數:

\[\begin{equation} \begin{aligned} J(\theta) = \frac 1 N \sum_{n=1}^{N} \sum_{t=1}^{T_n} R(\tau^n) \log p_\theta(a^n_t|s^n_t) \end{aligned} \end{equation} \]

對於同一個 Trajectory \(\tau\) 中, 針對每個狀態 \(s\) 下, 執行 動作 \(a\), 都有相同的 Reward 係數. 這是不合理的.
例如圖的左邊, 在 \(s_b\) 執行 \(a_2\) 不是一個好的選擇, 他會導致接下來進入 \(s_c\), 並執行 \(a_3\), 得到 -2 分.
由此, 提出改進1.

改進1: 每個時刻的 reward 改為, 當前時刻到結束時刻的 reward 的總和


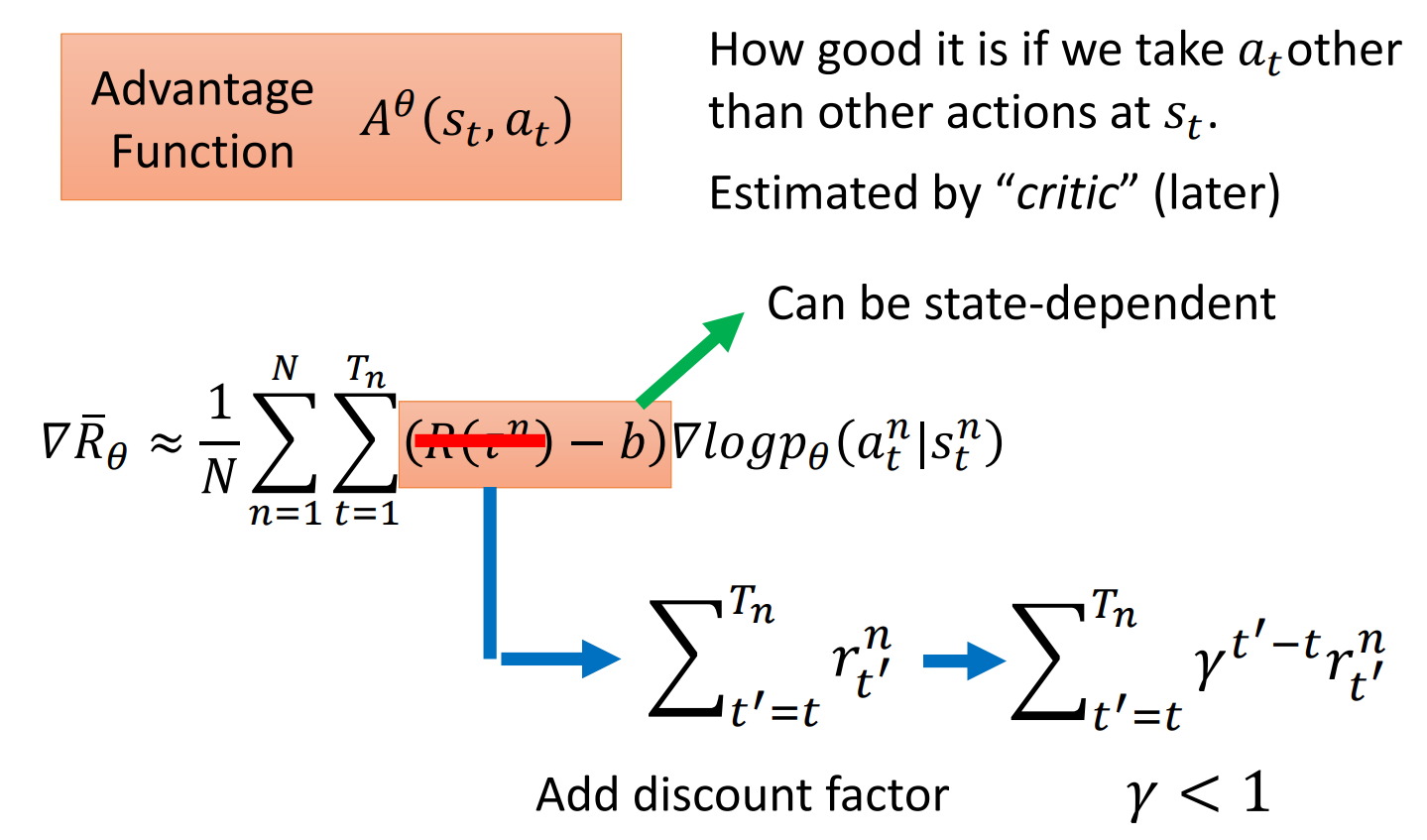
某時刻的 action, 經過越長時間, 它的影響力就越小. 也就是與該 action 間隔很久的 reward 與該 action 的關係很小. 由此提出改進2.

改進2: 加一個衰減係數.

最後, 將整個係數項稱為 Advantage Function, \(A^\theta(s_t, a_t)\).其含義為, 在某 state 下, \(a_t\) 相較於其他的 action, 有多好. (這個 \(A\), 通常可以是用一個網路來預測的 ???)

最終, 得梯度公式:

\[\begin{equation} \nabla \overline R_\theta \approx \frac 1 N \sum_{n=1}^{N} \sum_{t=1}^{T_n} A^\theta(s_t, a_t) \nabla\log p_\theta(a^n_t|s^n_t) \end{equation} \]

On-policy \(\rightarrow\) Off-policy

On-policy

梯度計算公式:

\[\begin{equation} \nabla \overline R_\theta =E_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla \log p_\theta(\tau)]\\ \end{equation} \]

目前為止的做法其實是一種 on-policy 的方法:

  • 每次更新梯度前, 都需要從 \(\pi_\theta\) 中取樣 \(\tau\).
  • 引數更新後, 又需要用更新後的引數重新取樣 \(\tau\).

目標是: 從另一個 policy, \(\pi_{\theta'}\) 中取樣資料, 用來訓練 \(\pi_\theta\). 這樣就可以重複利用這些取樣得到的資料.

Importance Sampling(重要性取樣)

\(x\) 服從 \(p\) 分佈時, 計算 \(f(x)\) 期望 \(E_{x\sim p}[f(x)]\) 的做法: 一般是從 \(p\) 中取樣一些 \(x\), 帶入 \(f(x)\) 求平均, 用這個值來估計所求期望.

現在, 假設無法從 \(p\) 中直接取樣 \(x\), 但可以從另一個分佈 \(q\) 中取樣 \(x\). 可以對 \(E_{x\sim p}[f(x)]\) 做如下變形:

\[\begin{equation} \begin{aligned} E_{x\sim p}[f(x)] &= \int f(x)p(x) \, dx\\ &=\int f(x)\frac{p(x)}{q(x)}q(x) \, dx\\ &= E_{x\sim q}[f(x)\frac{p(x)}{q(x)}] \end{aligned} \end{equation} \]

這樣, 我們就可以用 \(q\) 中取樣的資料來估計期望值 \(E_{x\sim p}[f(x)]\). 這就是 Importance Sampling.

Issue of Importance Sampling
理論上, 我們已經得出兩個期望值是相等的:

\[\begin{equation} E_{x\sim p}[f(x)] = E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]. \end{equation} \]

那麼它們的方差是否相等呢? \(Var_{x\sim p}[f(x)] == Var_{x\sim q}[f(x)\frac{p(x)}{q(x)}] ?\)

由公式

\[\begin{equation} Var[x] = E[x^2]-(E[x])^2 \end{equation} \]

可以得出:

\[\begin{equation} \begin{aligned} Var_{x\sim p}[f(x)]&=E_{x\sim p}[f^2(x)]-(E_{x\sim p}[f(x)])^2\\ Var_{x\sim q}[f(x)\frac{p(x)}{q(x)}] &=E_{x\sim q}[(f(x)\frac{p(x)}{q(x)})^2]-(E_{x\sim q}[f(x)\frac{p(x)}{q(x)}])^2\\ &=\int (f(x)\frac{p(x)}{q(x)})^2q(x) \, dx - (E_{x\sim p}[f(x)])^2\\ &=\int f^2(x)\frac{p(x)}{q(x)}p(x) \, dx - (E_{x\sim p}[f(x)])^2\\ &=E_{x\sim p}[f^2(x)\frac{p(x)}{q(x)}]-(E_{x\sim p}[f(x)])^2 \end{aligned} \end{equation} \]

對比發現, 第一項中後者比前者多乘了一個 \(\frac{p(x)}{q(x)}\), 也就是說當 \(p\) 與 \(q\) 相差很多時, 它們的方差也會差很多.

這樣就會出現一問題: 理論上, 無論 \(p,q\) 的分佈是什麼樣的, 當我們從 \(p\) 和 \(q\) 取樣足夠多次時, 是可以得到 \(E_{x\sim p}[f(x)] = E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]\) 的.
但是當 \(p,q\) 差距過大, 而我們取樣的次數又不夠多時, 因為它們之間的方差差距很大, 所以最後很可能導致期望差距很大.

一個直觀的例子:

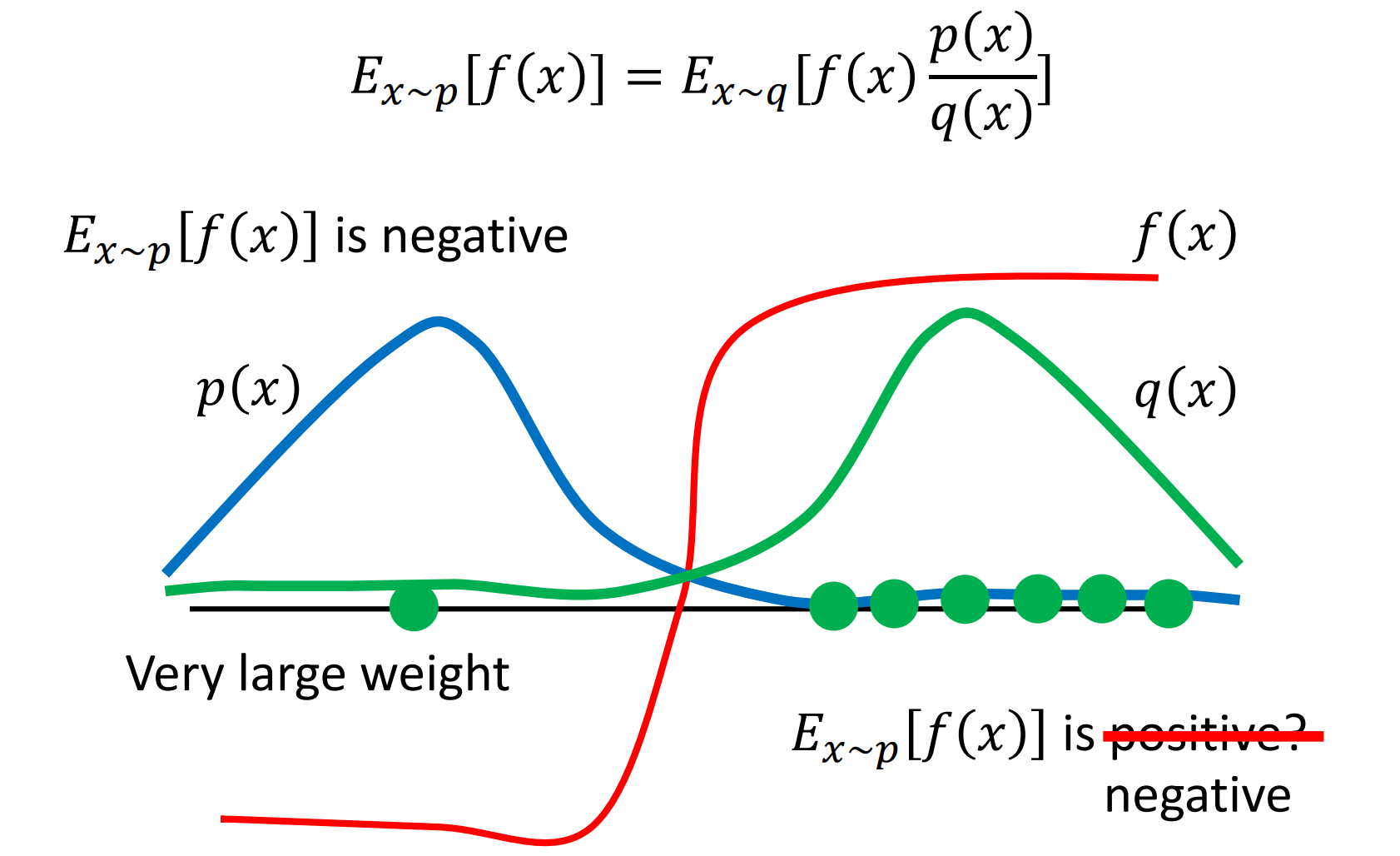
圖中 \(p,q\)兩個分佈的差異很大.

當我們取樣次數不夠多, 導致沒有取樣到最左邊那個樣本時, 就會出現實際上 \(E_{x\sim p}[f(x)]\) 應是一個負值, 但我們用 \(E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]\) 計算出來的卻是一個正值.

而當我們取樣到最左邊那個樣本時, 因為此時 \(\frac{p(x)}{q(x)}\) 的值將會非常大, 所以可以把 \(E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]\) 拉回負值.

Off-policy

將 Importance Sampling 用在 policy gradient 中, 我們就可以得到:

\[\begin{equation} \begin{aligned} \nabla \overline R_\theta &=E_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla \log p_\theta(\tau)]\\ &=E_{\tau\sim p_{\theta'}(\tau)}[\frac{p_{\theta}(\tau)}{p_{\theta'}(\tau)}R(\tau)\nabla \log p_\theta(\tau)] \end{aligned} \end{equation} \]

這樣, 我們就可以從 \(\theta'\) 中取樣資料, 然後多次利用這些資料來更新 \(\theta\).

結合公式(7), 得

\[\begin{equation} \begin{aligned} \nabla \overline R_\theta &=E_{\tau\sim p_{\theta'}(\tau)}[\frac{p_{\theta}(\tau)}{p_{\theta'}(\tau)}R(\tau)\nabla \log p_\theta(\tau)]\\ &=E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{p_\theta(s_t, a_t)}{p_{\theta'}(s_t, a_t)}A^{\theta'}(s_t, a_t) \nabla\log p_\theta(a^n_t|s^n_t)]\quad &&\text{由公式(7)得}\\ &=E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{p_\theta(a_t|s_t)p_\theta(s_t)}{p_{\theta'}(a_t|s_t)p_{\theta'}(s_t)}A^{\theta'}(s_t, a_t) \nabla\log p_\theta(a^n_t|s^n_t)]\\ &=E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{p_\theta(a_t|s_t)}{p_{\theta'}(a_t|s_t)}A^{\theta'}(s_t, a_t) \nabla\log p_\theta(a^n_t|s^n_t)]\quad &&\text{假設}p_\theta(s_t)=p_{\theta'}(s_t)\\ \end{aligned} \end{equation} \]

再由公式(3)得:

\[\begin{equation} \nabla \overline R_\theta=E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{\nabla p_\theta(a_t|s_t)}{p_{\theta'}(a_t|s_t)}A^{\theta'}(s_t, a_t)] \end{equation} \]

反推目標函數:

\[\begin{equation} J^{\theta'}(\theta)=E_{(s_t,a_t)\sim\pi_{\theta'}}[\frac{p_\theta(a_t|s_t)}{p_{\theta'}(a_t|s_t)}A^{\theta'}(s_t, a_t)] \end{equation} \]

Add constraint

目前為止, 我們利用 Importance Sampling 完成了 Policy Gradient 從 On-policy 到 Off-policy 的優化.

但是 Importance Sampling 在實際應用中有一個不得不考慮的限制, 就是我們無法保證能取樣足夠多的資料, 這時當兩個分佈 \(p_\theta, p_{\theta'}\)差異過大時, 難以保證期望相等.

PPO做的事情, 簡單說就是, 限制兩個分佈 \(p_\theta, p_{\theta'}\) 不能差太多.

\[\begin{equation} J_{PPO}^{\theta'}(\theta)=J^{\theta'}(\theta)-\beta KL(\theta, \theta') \end{equation} \]

注: 此處 KL 散度指的不是將兩個模型的引數看作分佈,拉近兩個模型的引數的距離. 而是兩個模型行為上的距離, 就是當兩個模型輸入同樣的 state 時, 希望輸出的 action 的分佈儘可能像

Conclusion

PPO algorithm

PPO2

PPO2: 簡化 PPO 的計算.

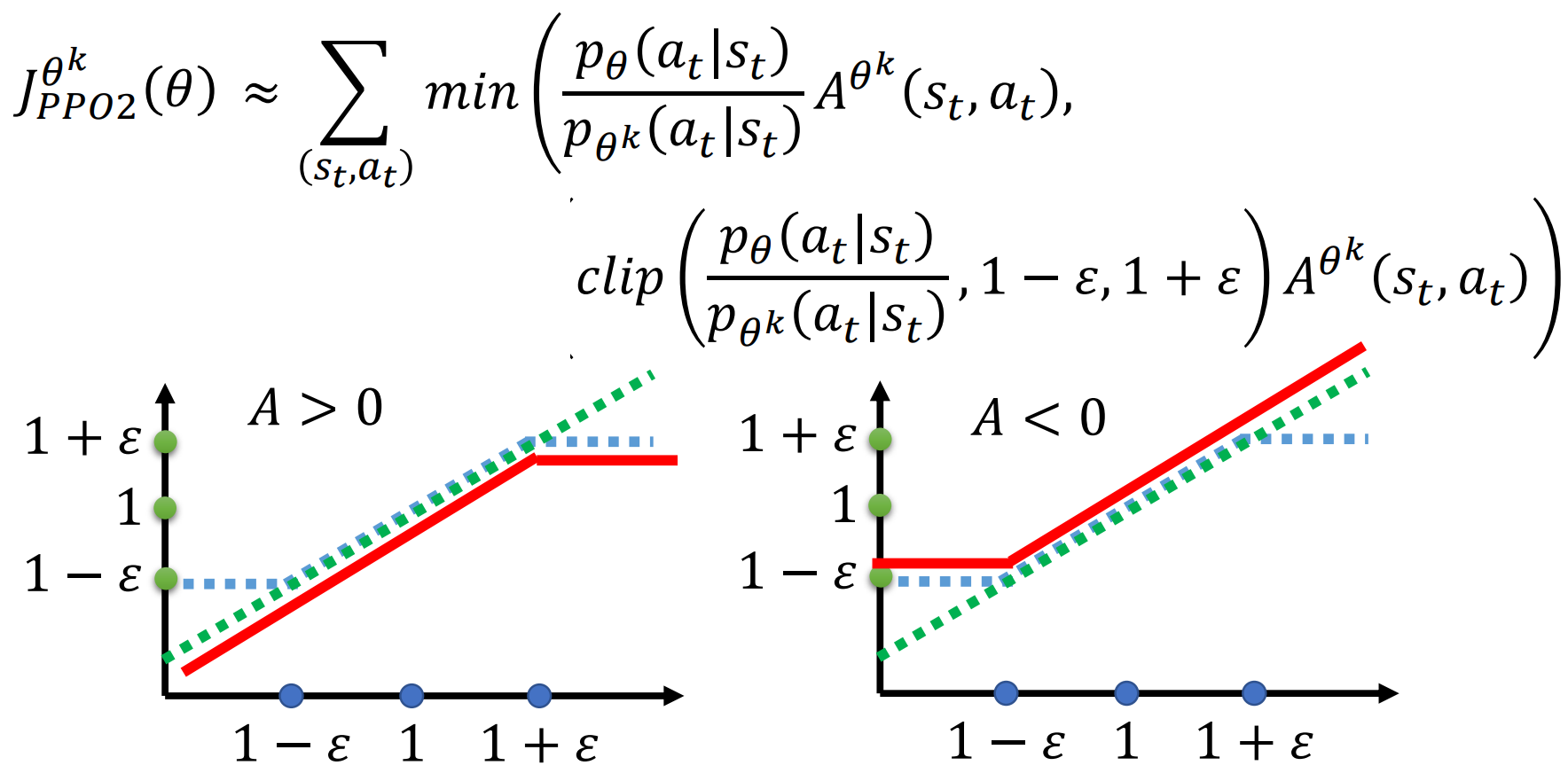
首先, 我們將橫座標 \(x\) 設為 \(\frac{p_\theta(a_t|s_t)}{p_{\theta^k}(a_t|s_t)}\), 則函數 \(y=x\) 與 \(y=clip(x, 1-\epsilon, 1+\epsilon)\) 的影象分別為圖中的綠線和藍線.
其中, \(clip(x, a, b)=\left\{\begin{aligned}a,\quad &x\le a\\ x, \quad &a<x<b\\ b, \quad &x \ge b\end{aligned}\right.\)

  • 當 \(A>0\) 時, \(J_{PPO2}^{\theta^k}(\theta)\) 就是左圖中紅線, 我們要最大化目標函數, 也就希望 \(x\) 越大越好, 但是當超過 \(1+\epsilon\) 後, 對目標函數就沒有 benefit 了.
  • 當 \(A<0\) 時, 同理, 如右圖.

目的依舊是保證兩個分佈 \(p_\theta, p_{\theta^k}\) 差距不能過大.

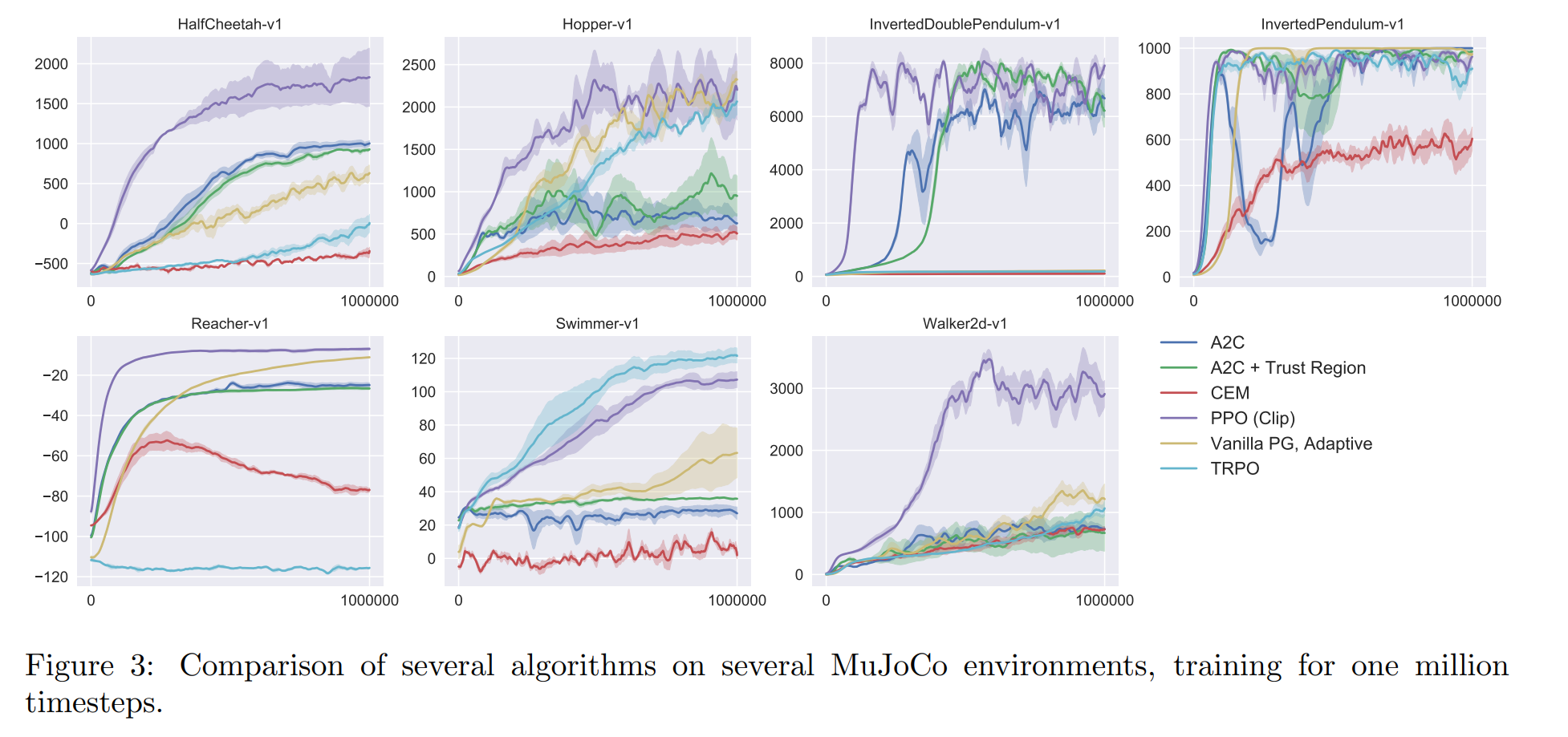
Experiment