Tarjan基礎用法
\(\operatorname{Tarjan}\) 基礎用法
\(\operatorname{Tarjan}\) 求最近公共祖先
前置芝士
最近公共祖先(Lowest Common Ancestor , LCA):一棵樹中兩個結點的 公共祖先裡面,離根最遠的那個被稱為最近公共祖先。我們記點集 \(S=\{v_1,v_2,\dots,v_n\}\) 的最近公共祖先為 \(\operatorname{LCA}(v_1,v_2,\dots,v_n)\) 或 \(\operatorname{LCA}(S)\)。
性質:
- \(\operatorname{LCA}(\{u\}=u)\);
- \(u\) 是 \(v\) 的祖先當且僅當 \(\operatorname{LCA}(u,v)=u\);
- 若 \(u\) 和 \(v\) 互相都不是對方的祖先,則 \(u,v\) 分別處於 \(\operatorname{LCA}(u,v)\) 的兩棵不同子樹中;
- 前序遍歷,\(\operatorname{LCA}(S)\) 出現在所有 \(S\) 中元素之前,後序遍歷,\(\operatorname{LCA}(S)\) 出現在所有 \(S\) 中元素之後;
- 兩點集的並的最近公共祖先為兩點集各自最近公共祖先的最近公共祖先,即\(\operatorname{LCA}(A \cup B)=\operatorname{LCA}(\operatorname{LCA}(A),\operatorname{LCA}(B))\);
- 兩結點的最近公共祖先一定在其這兩點最短路上
- 設 \(d\) 為樹上兩點間的距離,\(h\) 為一個點到樹根的距離,則 \(d_{uv}=h_u+h_v-2h(\operatorname{LCA}(u,v))\)
實現過程
請注意啦,\(\operatorname{Tarjan}\) 是一個離線演演算法,所以只能處理離線的 \(\operatorname{LCA}\) 詢問,線上需要使用其它方法。但是 \(\operatorname{Tarjan}\) 可以在一次搜尋後求出所有點對的 \(\operatorname{LCA}\),所以仍然具有研究價值。
- 首先我們要建立兩個連結串列,\(edge\) 用來存樹,而 \(qedge\) 用來儲存一種查詢關係,即對於一個點 \(u\),\(qedge\) 要記錄點 \(u\) 都與哪些其它點存在詢問;
- 接下來我們對整棵樹開始 \(\operatorname{DFS}\),用 \(vis\) 記錄是否存取過,用 \(fa_i\) 表示 \(i\) 的父親,由於 \(\operatorname{DFS}\) 的基本思想是每次只關心當前這一級,所以我們認為當前搜到的點 \(u\) 就是以 \(u\) 為根的子樹的根,
這句話看似是廢話其實也是廢話,這麼寫是為了提醒讀者在搜尋開始時要把這個點的父親設定為自己,也就是非常容易遺忘的初始化操作; - 回溯的時候將 \(fa_v\) 設定為 \(u\),也就是逐級遞迴找爸爸;
- 在回溯期間,如果包含當前節點的查詢的另一個結點也存取過了,就可以更新這兩個點的 \(\operatorname{LCA}\) 了;
- 最後統計輸出答案的時候,不要忘記使用剛剛我們學到的最後一個性質來輔助我們。
核心程式碼就長這樣:
void Tarjan(int u) {// 遞迴每一層都處理當前節點的子樹
fa[u] = u;// 初始化
vis[u] = true;
for (int i = head[u]; i; i = edge[i].next) {// 向下搜尋
int v = edge[i].to;
if (!vis[v]) {
Tarjan(v);
fa[v] = u;
}
}
for (int i = qhead[u]; i; i = qedge[i].next) {
// 搜尋並標記含有 u 結點的所有詢問
int v = qedge[i].to;
if (vis[v]) {// 兩個結點必須都被標記過
qedge[i].lca = find(v);// 標記 LCA
// 2n-1與2n的結果相同
if (i % 2) { qedge[i + 1].lca = qedge[i].lca; }
else { qedge[i - 1].lca = qedge[i].lca; }
}
}
}
例題
這就是個模板題,把上面那段程式碼套上去補完剩下的建圖部分就可以了,所以不必過多贅述。
參考程式碼:
#include <iostream>
#include <cstdio>
using namespace std;
namespace SHAWN {
const int N = 1e6 + 7;
int head[N], cnt;
int qhead[N], qcnt;
struct node { int to, next, lca; };
node edge[N], qedge[N];
int n, m, s;
int fa[N];
bool vis[N];
inline void add(int u, int v) {
edge[++cnt].next = head[u];
edge[cnt].to = v;
head[u] = cnt;
}
inline void qadd(int u, int v) {
qedge[++qcnt].next = qhead[u];
qedge[qcnt].to = v;
qhead[u] = qcnt;
}
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void Tarjan(int u) {
fa[u] = u;
vis[u] = true;
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (!vis[v]) {
Tarjan(v);
fa[v] = u;
}
}
for (int i = qhead[u]; i; i = qedge[i].next) {
int v = qedge[i].to;
if (vis[v]) {
qedge[i].lca = find(v);
if (i % 2) { qedge[i + 1].lca = qedge[i].lca; }
else { qedge[i - 1].lca = qedge[i].lca; }
}
}
}
int work()
{
cin >> n >> m >> s;
for (int i = 1, x, y; i < n; ++i) {
cin >> x >> y;
add(x, y); add(y, x);
}
for (int i = 1, x, y; i <= m; ++i) {
cin >> x >> y;
qadd(x, y); qadd(y, x);
}
Tarjan(s);
for (int i = 1; i <= m; ++i) {
cout << qedge[i << 1].lca << '\n';
}
return 0;
}
}
signed int main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
return SHAWN :: work();
}
\(\operatorname{Tarjan}\) 求割點、割邊
前置芝士
割點:在一個無向連通圖 \(G(V,E)\) 中,刪去結點 \(u\) 和與它相連的邊後,若該圖變為非連通圖,則稱結點 \(u\) 為該圖的割點(關節點)。
割邊:在一個無向連通圖 \(G(V,E)\) 中,刪去邊 \(e\) 後,若該圖變為非連通圖,則稱邊 \(e\) 為該圖的割邊(橋)。
如下圖中的 \(2\) 點和 \(6\) 點為割點,邊 \((1,2)\) 和邊 \((6,7)\) 為割邊:
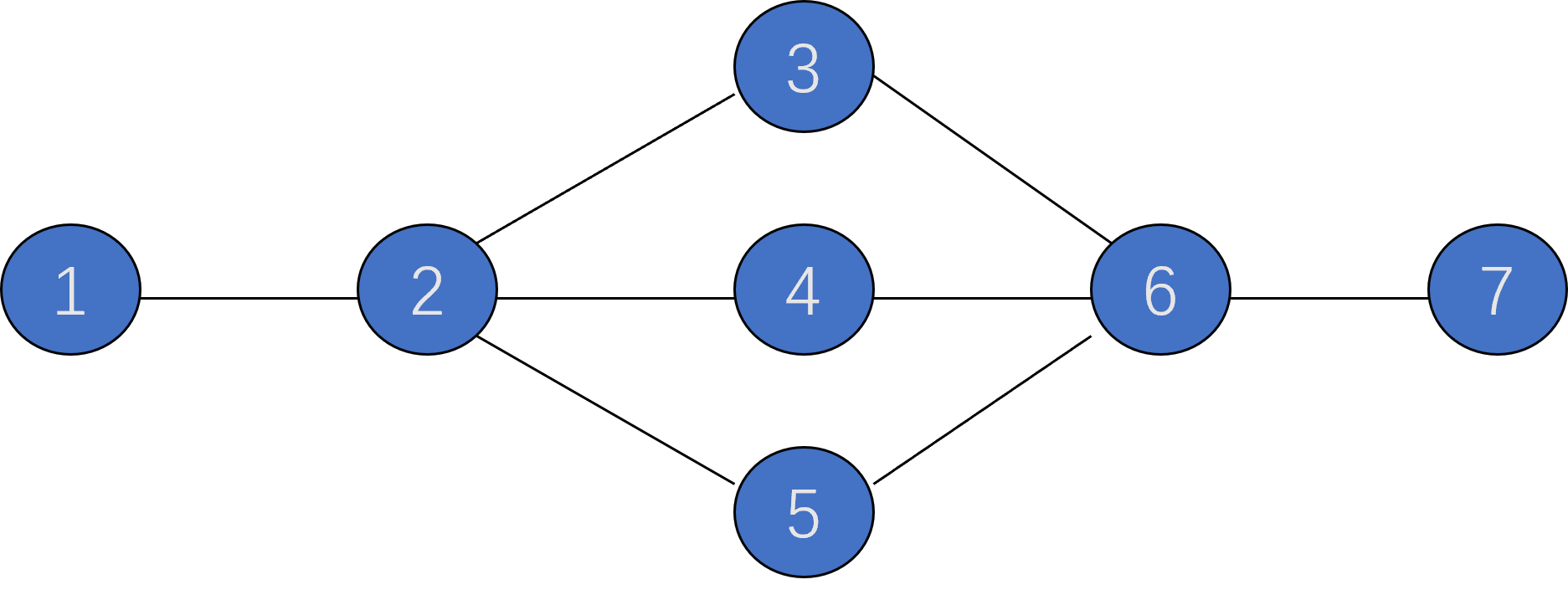
重連通圖:一個不含割點的連通圖稱為重連通圖(雙連通圖)。重連通無向圖重每對頂點之間至少存在兩條路徑,下圖就是一個重連通圖:
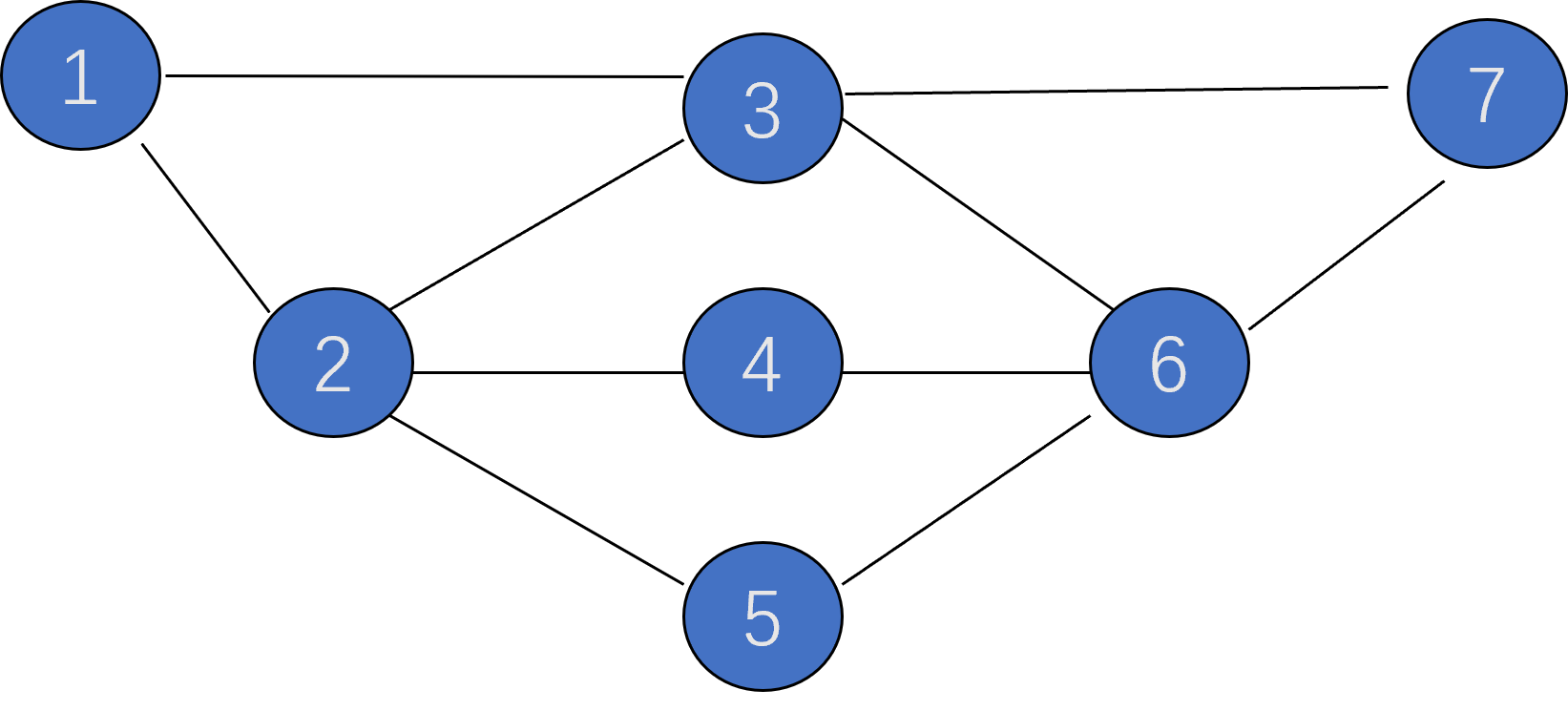
一些性質:
- 兩個割點之間的邊不一定是割邊
- 割邊的兩個端點不一定都是割點,但一定有一個是割點
\(\operatorname{Tarjan}\) 求割點
比方說我們對剛剛這個圖求割點:

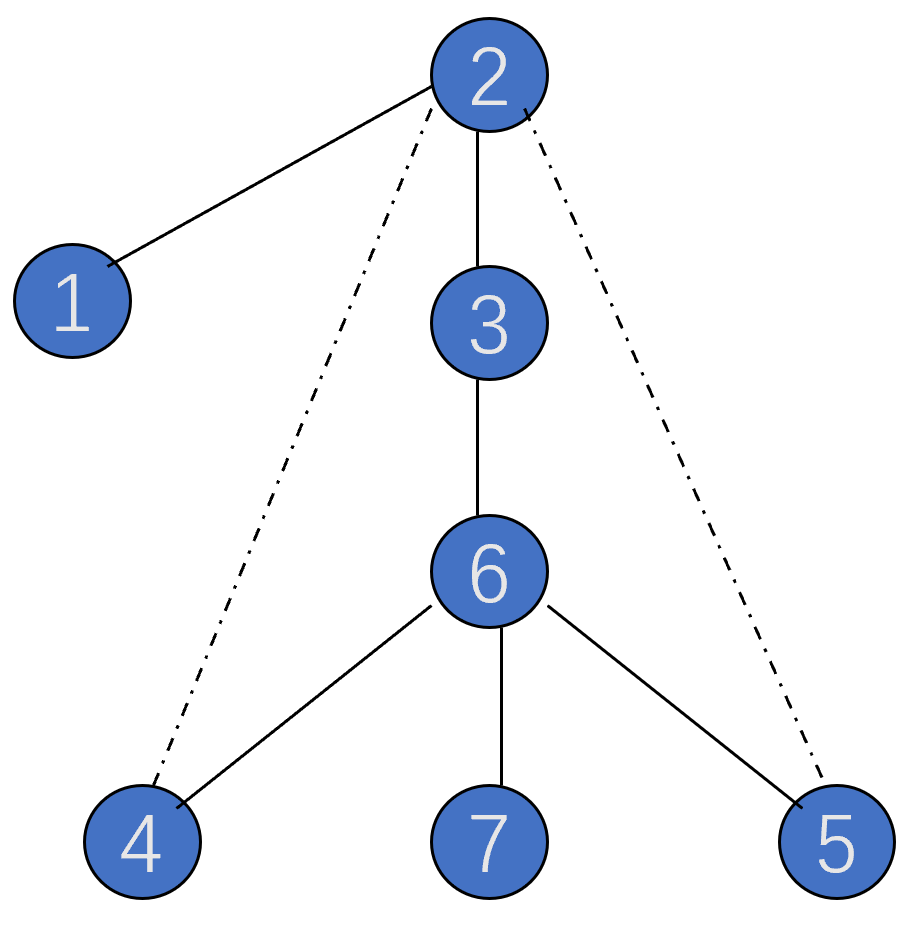
我們從結點 \(2\) 開始深度優先遍歷,可以得到如下深度優先生成樹,實線邊構成樹邊,虛線邊構成回邊:
設原圖為 \(G(V,E)\),其深度優先生成樹為 \(T(V,E)\) ,則 \(G\) 和 \(T\) 具有如下的性質:
- \(\forall u \in V(T)\) ,要麼是根,要麼不是根
- \(u\) 為根時,\(u\) 是割點 $\Leftrightarrow $ \(u\) 有 \(2\) 棵或 \(2\) 棵以上的子樹
- \(u\) 不為根時,\(u\) 是割點 $\Leftrightarrow $ \(u\) 存在兒子 \(v\) 使得 \(low_v \ge dfn_u\)
我們發現性質裡有一些陌生的東西,\(dfn\) 和 \(low\),這兩個東西分別叫做深度優先數和最低深度優先數。我們在剛剛 \(\operatorname{DFS}\) 遍歷的時候按照 \(\operatorname{DFS}\) 序給每個結點打上時間戳,這些時間戳就是深度優先數,我們用 \(dfn\) 陣列來儲存它。如上圖生成樹中,\(dfn_2=1\),\(dfn_1=2\),\(dfn_3=3\),\(dfn_4=5\),\(dfn_5=6\),\(dfn_6=4\),\(dfn_7=7\)。而最低深度優先數 \(low\) 則表示從結點 \(u\) 出發能到達的點的最小深度優先數,其決定式如下:
那麼知道了這些我們再回過頭去看剛剛第三個性質,當 \(v\) 是 \(u\) 的兒子且 \(low_v<dfn_u\) 時,以 \(v\) 為根節點的子樹中必然有節點與 \(u\) 的祖先有回邊,如果 \(u\) 的任意兒子都滿足這個特點時,\(u\) 顯然不是割點。
參考程式碼:
namespace SHAWN {
const int N = 2e5 + 7;// 雙向邊開二倍空間
int head[N], cnt;
struct edge{ int to, next; }edge[N];
int dfn[N], low[N];
bool used[N], flag[N];
int n, m, res, tim;
inline void add(int u, int v) {
edge[++cnt].next = head[u];
edge[cnt].to = v;
head[u] = cnt;
}
void Tarjan(int u, int fa) {
used[u] = true;
low[u] = dfn[u] = ++tim;
int child = 0;
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (!used[v]) {
if (fa == u) { ++child; }
Tarjan(v, u);
// 如果v是u的孩子
low[u] = min(low[u], low[v]);
// 如果u不是根且low[u] >= dfn[u]就是割點
if (fa != u && low[v] >= dfn[u] && !flag[u]) {
flag[u] = true;
++res;
}
}
// 如果(u,v)是一條回邊
else if (fa != v) {
low[u] = min(low[u], dfn[v]);
}
}
// 如果u是根且有兩個或兩個以上子樹就是割點
if (fa == u && child >= 2 && !flag[u]) {
flag[u] = true;
++res;
}
}
int work()
{
cin >> n >> m;
for (int i = 1, x, y; i <= m; ++i) {
cin >> x >> y;
add(x, y); add(y, x);
}
// 不保證連通所以要多次跑
for (int i = 1; i <= n; ++i) {
if (!used[i]) {
tim = 0;
Tarjan(i, i);
}
}
cout << res << '\n';
for (int i = 1; i <= n; ++i) {
if (flag[i]) { cout << i << ' '; }
}
return 0;
}
}
\(\operatorname{Tarjan}\) 求割邊
設原圖為 \(G(V,E)\),其深度優先生成樹為 \(T(V,E)\) ,則 \(G\) 和 \(T\) 滿足如下定理:
\(\exists u,v \in T\),\(u\) 是 \(v\) 的雙親,\(u,v\) 之間的邊不是有重邊,則 \((u,v)\) 是割邊 $\Leftrightarrow $ \(u\) 到 \(v\) 的邊不是重邊且 \(v\) 或 \(v\) 的子孫結點中沒有指向 \(u\) 或著 \(u\) 的祖先的回邊。即 \((u,v)\) 是割邊 \(\Leftrightarrow\) \(dfn_u<low_v\)。
然後我們把剛剛程式碼稍微改一改就出來了,像這樣:
void Tarjan(int u, int fa) {
par[u] = fa;
low[u] = dfn[u] = ++tim;
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (!dfn(v)) {
Tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
flag[v] = true;
++res;
}
}
else if (dfn[v] < dfn[u] && v != fa) }{
low[u] = min(low[u], dfn[v]);
}
}
}
最後當 \(flag_u\) 為真時,邊 \((u,par_u)\) 就是割邊。
參考程式碼:
namespace SHAWN {
const int N = 1e4 + 7;
int head[N], cnt;
struct edge { int to, next; }edge[N];
struct node { int a, b; };
int dfn[N], low[N];
int n, m, tim;
struct cmp{
bool operator() (const node &x, const node &y) const {
if (x.a != y.a) { return x.a > y.a; }
else { return x.b > y.b; }
}
};
priority_queue<node, vector<node>, cmp> q;
inline void add(int u, int v) {
edge[++cnt].next = head[u];
edge[cnt].to = v;
head[u] = cnt;
}
void Tarjan(int u, int fa) {
low[u] = dfn[u] = ++tim;
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (!dfn[v]) {
Tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
q.push({u,v});
}
}
else if (dfn[v] < dfn[u] && v != fa) {
low[u] = min(low[u], dfn[v]);
}
}
}
int work()
{
cin >> n >> m;
for (int i = 1, x, y; i <= m; ++i) {
cin >> x >> y;
add(x, y); add(y, x);
}
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) {
Tarjan(i, i);
}
}
while (!q.empty()) {
auto it = q.top(); q.pop();
cout << it.a << ' ' << it.b << '\n';
}
return 0;
}
}
例題
題目分析
題目要求我們刪掉一個點使得給定的兩個點不連通,那麼其實我們就是要找一個滿足要求的割點,如下圖示黑的點就是題目給定的兩個點:
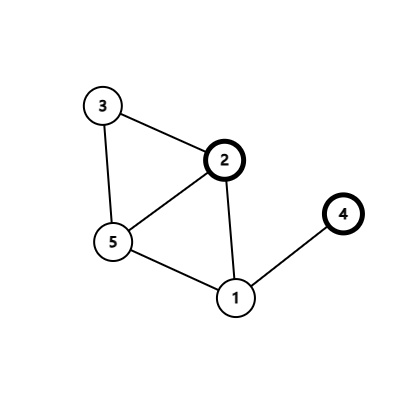
點 \(1\) 是一個割點,我們刪除點 \(1\) 即可使得 \(2,4\) 兩點不連通,但是並非任意割點都滿足要求,比方說下面這張圖:
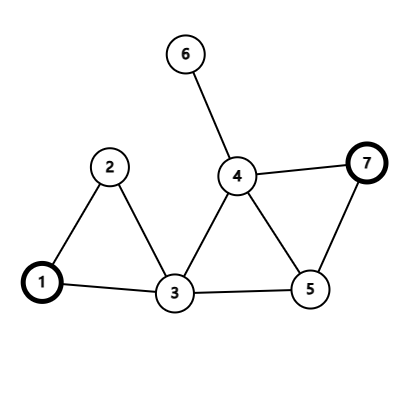
點 \(3\) 和點 \(4\) 都是圖中的割點,但是刪去 \(4\) 並不能使得目標點 \(1,7\) 不連通,所以只有點 \(3\) 是符合條件的點,那麼我們就要去篩選割點中符合要求的點。
怎麼篩呢?其實我們想一想建立 \(\operatorname{DFS}\) 樹的過程,我們從題中給定的一個點開始搜,那麼對於一個符合條件的割點來講,題中給定的另一個點一定在這個符合條件的割點的子樹中。所以在搜的時候加個判斷條件就好了。本題因為不能刪去根,所以不用考慮根是割點的情況,那麼程式碼也就非常簡單:
#include <iostream>
#include <cstdio>
using namespace std;
namespace SHAWN {
const int N = 1e6 + 7;
int head[N], cnt;
struct edge { int to, next; }edge[N];
int n, tim, x, y;
int dfn[N], low[N];
bool vis[N], flag[N];
inline void add(int u, int v) {
edge[++cnt].next = head[u];
edge[cnt].to = v;
head[u] = cnt;
}
void Tarjan(int u, int fa) {
low[u] = dfn[u] = ++tim;
vis[u] = true;
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (!vis[v]) {
Tarjan(v, u);
low[u] = min(low[u], low[v]);
// 這裡多加一個u!=x和dfn[y]>=dfn[v]的特判就OK了
if (fa != u && low[v] >= dfn[u] && u != x && dfn[y] >= dfn[v]) {
flag[u] = true;
}
}
else if (fa != v) {
low[u] = min(low[u], dfn[v]);
}
}
}
int work()
{
cin >> n;
while (cin >> x >> y && x && y) {
add(x, y); add(y, x);
}
cin >> x >> y;
Tarjan(x, x);
for (int i = 1; i <= n; ++i) {
if (flag[i]) {
cout << i << '\n';
return 0;
}
}
cout << "No solution\n";
return 0;
}
}
signed int main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
return SHAWN :: work();
}
2、割邊 [CEOI2005] Critical Network Lines
題目分析
與上一道題一樣,我們顯然可以看出來題目想讓我們求出滿足下面條件的割邊——刪掉這條邊後剩下的兩個連通塊中至少一個塊只包含 \(A\) 類點或 \(B\) 類點。比如下圖(圖中邊上的數位是編號不是邊權):
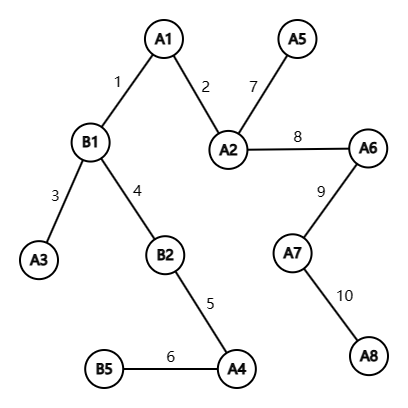
這幅圖中的割邊有 \(1,4,5,6,8\) 五條,而符合題目條件的只有 \(1,6,8\) 這三條。我們發現,當一個割邊滿足條件當且僅當它連線的一個節點在深度優先生成樹中的子樹內只包含一類點。所以我們在 \(\operatorname{Tarjan}\) 求割邊的時候,每找到一條割邊 \((u,v)\),我們就檢查一下以 \(v\) 為根結點的子樹內 \(A\) 和 \(B\) 類結點各自的數量,當其中一個個數為 \(0\) 或者全滿,就是要求的邊,打上標記並給計數的答案加一就可以了。求數量的過程,可以在 \(\operatorname{DFS}\) 的時候遞迴計算。下面是 AC 程式碼:
#include <iostream>
#include <cstdio>
using namespace std;
namespace SHAWN {
const int N = 2e6 + 7;
// 請注意這裡一定要開二倍空間,要不然會寄
int head[N], cnt;
struct edge { int to, next; }edge[N];
int n, m, a, b, tim, res;
int dfn[N], low[N], acnt[N], bcnt[N], par[N];
// acnt[i]表示i結點子樹中A類點數量,bcnt同理
// par用來記每個結點在dfs生成樹中的父親
bool flag[N];
inline void add(int u, int v) {
edge[++cnt].next = head[u];
edge[cnt].to = v;
head[u] = cnt;
}
void Tarjan(int u, int fa) {
low[u] = dfn[u] = ++tim;
par[u] = fa;
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (!dfn[v]) {
Tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
if (!acnt[v] || !bcnt[v] || acnt[v] == a || bcnt[v] == b) {
// A類或B類有一個為0或全滿就說明符合要求
flag[v] = true;
++res;
}
}
acnt[u] += acnt[v]; bcnt[u] += bcnt[v];
// 從下向上遞迴統計子樹情況
}
else if (dfn[v] < dfn[u] && fa != v) {
low[u] = min(low[u], dfn[v]);
}
}
}
int work()
{
cin >> n >> m >> a >> b;
for (int i = 1, x; i <= a; ++i) { cin >> x; acnt[x] = 1; }
for (int i = 1, x; i <= b; ++i) { cin >> x; bcnt[x] = 1; }
// 最開始每個點的子樹就是自己
for (int i = 1, x, y; i <= m; ++i) {
cin >> x >> y;
add(x, y); add(y, x);
}
Tarjan(1, 0);
cout << res << '\n';
for (int i = 1; i <= n; ++i) {
if (flag[i]) {
cout << i << ' ' << par[i] << '\n';
}
}
return 0;
}
}
signed int main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
return SHAWN :: work();
}
\(\operatorname{Tarjan}\) 求強連通分量
前置芝士
強連通:在有向圖 \(G\) 中,如果兩個頂點 \(u_i,u_j\) 間 \((u_i \ne u_j)\) 有一條從 \(u_i\) 到 \(u_j\) 的有向路徑,同時還有一條從 \(u_j\) 到 \(u_i\) 的有向路徑,則稱兩個頂點強連通(Strongly Connected, SC)。
強連通圖:有向圖 \(G\) 中,若任意兩點強連通,則稱 \(G\) 是一個強連通圖。
強連通分量(Strongly Connected Components, SCC):極大的強連通子圖。
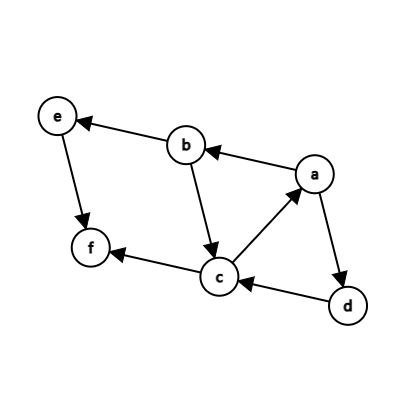
如圖是一個強連通圖,圖上的強連通分量有三個:\(a-b-c-d,e,f\)。
縮點:因為強連通圖中任意兩點連通,所以在不考慮路徑長度只考慮連通性的情況下,可以將一個強連通分量壓縮成一個點來進行處理,這樣就可以縮小圖的規模。
實現過程
我們演演算法的主要過程與步驟如下:
- 從根開始向下搜尋,實時更新 \(dfn\) 和 \(low\),每搜到一個點就入棧;
- 當 \(v\) 未被存取過,我們繼續深搜,在回溯過程中,用 \(low_v\) 更新 \(low_u\),當回溯到某一個點 \(u\) 使得 \(dfn_u=low_u\) 時,彈棧直到把自己也彈出來,這些彈出來的元素就是一個強連通分量;
- 當 \(v\) 被存取過且已經在棧中,就像前面一樣用 \(dfn_v\) 更新 \(low_u\);
- 當 \(v\) 被存取過且不在棧中,不操作。
下面給出一個例子來幫助讀者理解這一過程:
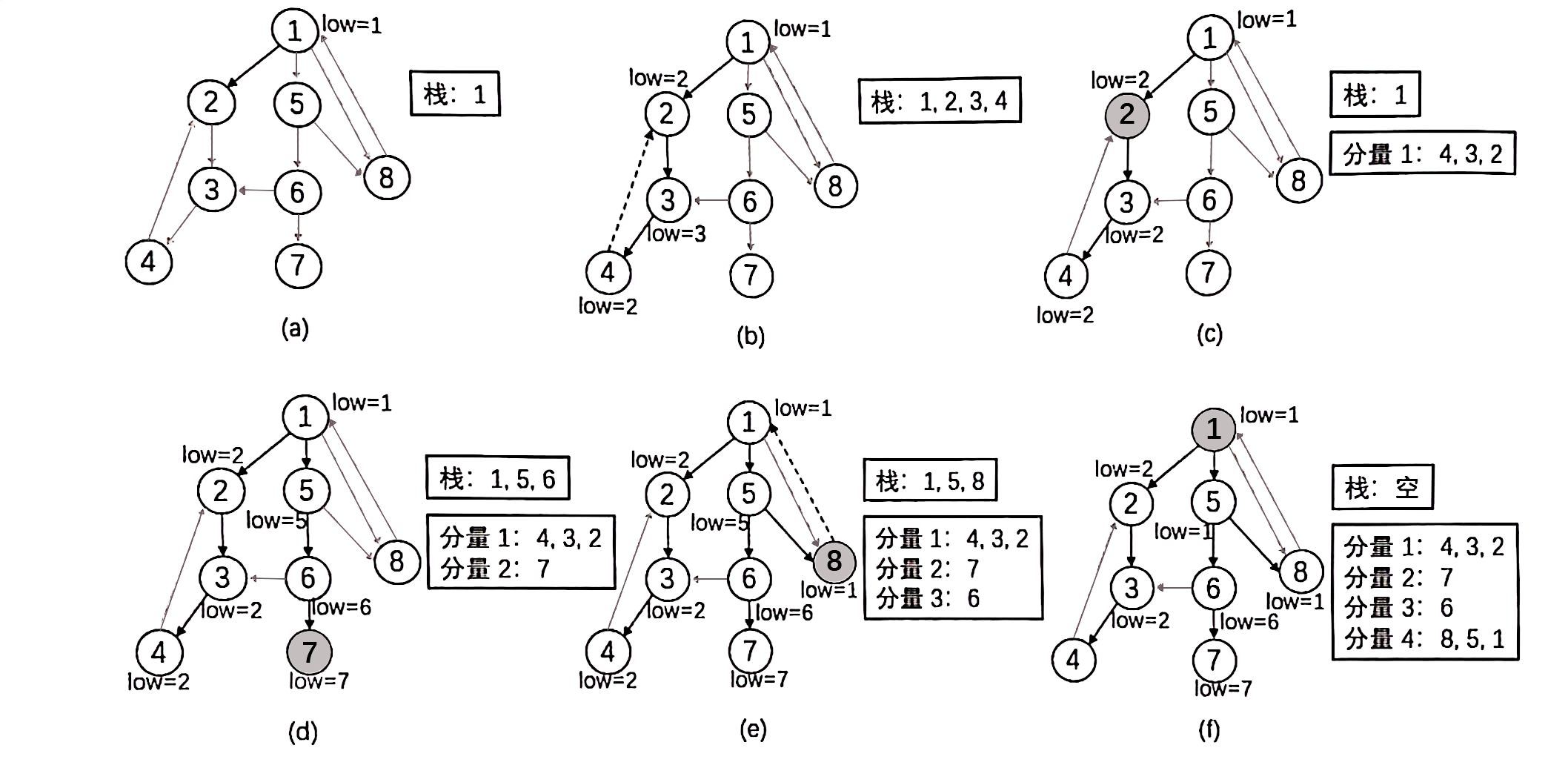
- 如圖 (a),從 \(1\) 開始搜,\(1\) 入棧,\(dfn_1=low_1=1\);
- 如圖 (b),搜到 \(2\),\(2\) 入棧,搜到 \(3\),\(3\) 入棧,搜到 \(4\),\(4\) 入棧,接下來通過返祖邊搜到了 \(2\),\(low_4=2\);
- 如圖 (c),返回 \(3\),\(low_3=2\),返回 \(2\),\(low_2=2\),此時 \(low_2=dfn_2=2\),所以找到了一個強連通分量,彈棧直到自己得到連通分量 \(\{2,3,4\}\);
- 如圖 (d),返回 \(1\),搜到 \(5\) 入棧,搜到 \(6\) 入棧,連向 \(3\) 有一條橫向邊,但 \(3\) 不在棧裡,所以不管,搜到 \(7\) 入棧,然後搜不下去了,\(low_7=dfn_7=7\),彈棧直到自己得到連通分量 \(\{7\}\);
- 如圖 (e),返回 \(6\),\(low_6=dfn_6=6\),彈棧知直到自己得到連通分量 \(\{6\}\),回到 \(5\),存取過了但是 \(dfn\) 和 \(low\) 更新後沒變,搜到 \(8\),接下來通過返祖邊搜到了 \(1\),\(low_8=1\);
- 如圖 (f),返回 \(5\),\(low_5=1\),返回 \(1\),前向邊搜到 \(8\),更新後沒變所以不管,返回 \(1\),\(low_1=dfn_1=1\),彈棧直到自己得到連通分量 \(\{1,5,8\}\)。
程式碼大概就長這樣:
namespace SHAWN {
const int N = 1e5 + 10;
int head[N], cnt;
struct edge { int to, next; }edge[N];
int n, m, tim, top, idx;
int dfn[N], low[N], st[N], size[N], scc[N];
bool chkin[N];
inline void add(int u, int v) {
edge[++cnt].next = head[u];
edge[cnt].to = v;
head[u] = cnt;
}
void Tarjan(int u) {
low[u] = dfn[u] = ++tim;
st[++top] = u;// 搜到就入棧
chkin[u] = true;
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (!dfn[v]) {
Tarjan(v);
low[u] = min(low[u], low[v]);
}
else if (chkin[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
//low[u]=dfn[u]時彈棧直到自己
int v; ++idx;
do {
v = st[top--];
scc[v] = idx;
chkin[v] = false;
++size[idx];
} while (v != u);
}
}
int work()
{
cin >> n >> m;
for (int i = 1, x, y; i <= m; ++i) {
cin >> x >> y;
add(x, y);
}
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) {
Tarjan(i);
}
}
int ans = 0;
for (int i = 1; i <= idx; ++i) {
ans += (size[i] > 1);
}
cout << ans << '\n';
for (int i = 1; i <= n; ++i) {
cout << scc[i] << ' ';
}
return 0;
}
}
例題
1、P2341 USACO03FALL / HAOI2006 受歡迎的牛 G
我們考慮如何建模。一隻奶牛喜歡另一隻奶牛可以表示為有向圖上的一條有向邊,因為愛慕關係具有傳遞性,所以能和其餘所有點都連通的結點就是一個可行答案。我們如何去優化這個問題呢?考慮在強連通分量中,因為所有點都互相連通,所以我們可以進行縮點。縮點後如果只有一個出度為 \(0\) 的點,那麼答案就是這個強連通分量中包含的結點個數。如果有多個出度為 \(0\) 的點或根本沒有出度為 \(0\) 的點,就沒有明星牛。這怎麼理解呢?縮點以後點內奶牛不再互相愛慕,對於整個圖,只有不愛慕別的牛的牛才能成為明星奶牛(看看,多不好),但如果大家都不愛慕別的牛了顯然也不符合要求,所以我們有了這樣的判斷。那麼程式碼就是上面的題小改了一下:
#include <iostream>
#include <cstdio>
using namespace std;
namespace SHAWN {
const int N = 5e4 + 7;
int head[N], cnt;
struct edge { int to, next; }edge[N];
int n, m, tim, top, idx, cont, ans;
int dfn[N], low[N], size[N], sta[N], scc[N], diag[N];
bool chkin[N];
inline void add(int u, int v) {
edge[++cnt].next = head[u];
edge[cnt].to = v;
head[u] = cnt;
}
void Tarjan(int u) {
low[u] = dfn[u] = ++tim;
sta[++top] = u;
chkin[u] = true;
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (!dfn[v]) {
Tarjan(v);
low[u] = min(low[u], low[v]);
}
else if (chkin[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
int v; ++idx;
do {
v = sta[top--];
scc[v] = idx;
chkin[v] = false;
++size[idx];
} while (v != u);
}
}
int work()
{
cin >> n >> m;
for (int i = 1, x, y; i <= m; ++i) {
cin >> x >> y;
add(x, y);
}
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) {
Tarjan(i);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = head[i]; j; j = edge[j].next) {
int v = edge[j].to;
if (scc[i] != scc[v]) {
++diag[scc[i]];
}
}
}
for (int i = 1; i <= idx; ++i) {
if (!diag[i]) {
++cont;
ans += size[i];
}
}
if (cont == 1) { cout << ans << '\n'; }
else { cout << "0\n"; }
return 0;
}
}
signed int main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
return SHAWN :: work();
}
總結
我們總共總結了 \(\operatorname{Tarjan}\) 演演算法的三種主要用法,其實與其說它是一種演演算法,不如說它是一種 \(\operatorname{DFS}\) 時的思想,也就是通過對於圖上點先後存取關係來形成一棵 \(\operatorname{DFS}\) 生成樹,用回溯的方法在樹上對點對之間的關係進行操作和處理,最終得到我們想要的最近公共祖先,割點,割邊或者強連通分量。而我們在運用這些方法的時候也要做到靈活變通,仔細考慮題目中給定的點邊關係,然後再將統計答案的步驟加入到搜尋的過程中來通過遞迴和篩選得到我們想要的答案。
以上內容如有錯誤或不嚴謹的地方,請各位巨佬指正,orz
參考文獻
- 汪星明 Tarjan相關演演算法及其應用
- OI-Wiki 最近公共祖先
- 江嶼 tarjan演演算法求LCA
- OI-Wiki 割點和橋
- OI-Wiki 強連通分量
- 洛谷網校《深入淺出程式設計競賽進階篇》